基于近似边界和层次聚类的超多目标进化算法
2020-12-25顾一凡
张 峰,顾一凡
(南京航空航天大学 计算机科学与技术学院,江苏 南京 211100)
0 引 言
在实际工程优化问题中,往往需要同时优化多个冲突的目标,这类问题就被称为多目标优化问题[1-2](multiobjective optimization problem,MOP)。目标数大于3的多目标优化问题,就被称为超多目标优化问题(many-objective optimization problem,MaOP)。许多工程优化问题都属于超多目标优化问题,高效地求解超多目标优化问题有着十分重要的理论意义和实际价值。
1 概 述
1.1 超多目标优化问题定义
一个连续的最小化超多目标优化问题(MaOP)的数学表达式如下:
(1)
其中,Ω∈Rn和F:Ω→Rm分别表示决策空间和m个实值目标函数组成的目标空间,x=(x1,x2,…,xn)T∈Ω称为MaOP中的一个解。
1.2 相关定义简介
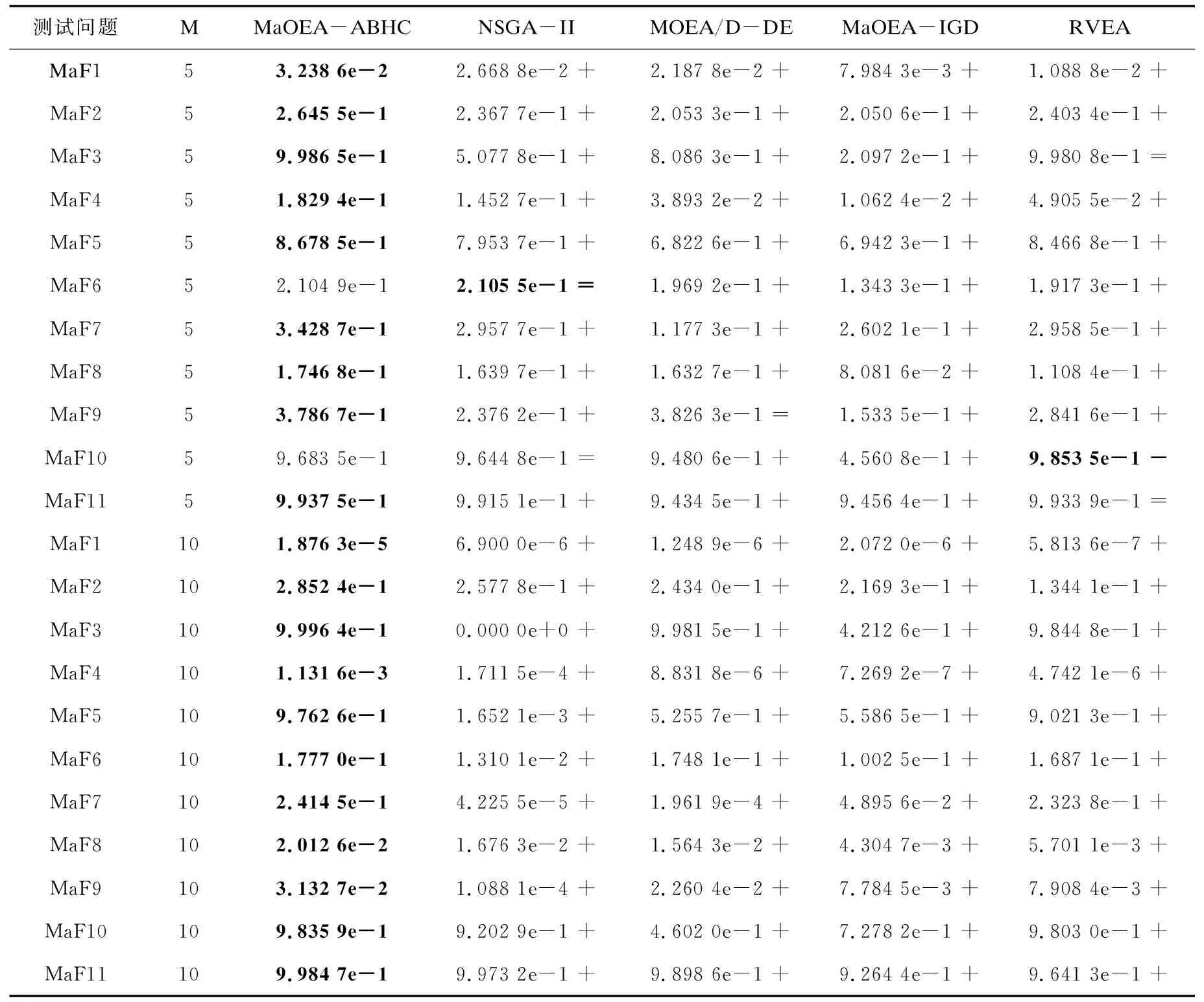
假设两个解u,v∈Ω,定义u支配v并简记为uv,成立的条件是当且仅当对∀j∈{1,2,…,m}都有fj(u)≤fj(v),并且至少∃i∈{1,2,…,m}使得fi(u) 理想点z*的定义如下: (2) 极值点znad的定义如下: (3) 其中,P'表示一个解集P的非支配解集。 决策者可以根据实际需要从算法近似的PF中挑选一个解进行决策。 收敛性和多样性是衡量多目标优化算法性能的准则。收敛性是指算法近似出来的PF距离真实PF的远近,多样性是指算法近似的PF能否很好地覆盖和表示整个PF。 在过去的几十年中,许多经典的多目标优化算法被提出来求解MOP,而多目标进化算法能够通过进行大量目标函数评估来有效求解MOP。下面简单介绍一些多目标进化算法。 NSGA-II[4]能够通过快速非支配排序和计算拥挤距离来有效求解2到3目标的MOP,但在求解MaOP上,会出现许多非支配解,导致算法性能难以达到理想的效果。MOEA/D-DE[5]通过结合基于一组权重向量分解的方法和差分进化来有效求解一些具有复杂PS形状的MOP,但由于算法中的权重向量是固定的,这不一定能很好地适应PF形状,在求解一些PF形状特殊的MaOP,MOEA/D-DE效果欠佳。为了更好地平衡算法在高维目标空间上的收敛性和多样性,RVEA[6]通过一种角度惩罚距离的度量方法来自适应地调整权重向量分布,因此,RVEA能够较好地求解MaOP问题。在一种被广泛使用的评价指标Inverted Generational Distance[7](IGD)上,MaOEA/IGD[8]设计了一种高效计算支配比较的方法和提出了一种基于分解的高效近似极值点的方法,来更好地求解MaOP。尽管上述的多目标进化算法能够从基于支配、分解和指标的角度来较好地求解MaOP问题,但由于MaOP目标空间过于庞大,算法使用的种群数量有限,如何在求解MaOP时更好地考虑算法的收敛性和多样性一直是一个严峻的挑战。 Singh和Isaacs等人定义了角点解并提出一种求出角点解的方法[9]。角点解可能出现在以下这两种极端的情况。(1)角点解位于一个只有某个目标最小的超平面上;(2)角点解位于轴坐标上,原点在理想点上。 角点解可以用来有效近似极值点。假设SC是一个角点解集,极值点的近似公式如下所示: (4) 在求解MOP时,平衡多样性和收敛性是提升算法性能的关键。但在求解MaOP时,由于目标空间过大,并且算法往往只能使用数量较少的种群来近似问题的PF,这使得许多算法更难以较好地保持多样性和收敛性。此外,大多数算法忽略了使用近似的极值点来固定近似的PF边界,这会影响MaOP的求解速度。为了充分利用极值点的有效信息,该文使用一种求角点解的方法[9]来近似极值点,和使用极值点固定近似的PF边界来排除比较差的解,借此来加速算法收敛,然后进一步提出使用层序聚类的方法来将种群划分成多个聚类,并根据每个聚类中心自适应地产生一个权重向量,最后根据每个聚类中的解在对应权重向量的聚合函数来挑选下一代种群。通过上述方法使得算法能够保持较好的收敛性和多样性并有效地求解MaOP。 本节主要介绍提出的基于层次聚类和边界近似的超多目标进化算法(MaOEA-ABHC)的实现细节,其中MaOEA表示超多目标进化算法,ABHC表示边界近似和层次聚类。MaOEA-ABHC的算法框架如算法1所示: 算法1:MaOEA-ABHC算法框架。 输入:N:种群数; 算法的终止条件。 输出:最终种群P。 1.随机生成规模为N的初始种群P; 2.while 没达到终止条件 do 3.对P使用SBX算子产生子代Q; 4.PU=P∪Q; 5.使用PU近似z*; 6.根据PU求出角点解集SC并近似znad; 7.P=UpdatePop(N,PU,SC,z*,znad); 8.end 9.returnP MaOEA-ABHC主要分为3个阶段: (1)初始化:主要随机生成一个规模为N的初始种群P。 (2)近似边界:首先对当前种群P使用SBX算子来产生子代Q,然后根据式(5)来近似理想点z*: (5) 根据Singh和Isaacs等人的工作[9]求出当前PU的角点解集SC,最后根据式(4)使用SC来近似极值点znad。 (3)更新种群:根据PU非支配解的数量与种群数的相应情况来更新当前种群P。 更新种群相对比较复杂,首先获取PU的非支配解集P'和剩余解集PR。 接下来进行第一次判断,如果P'的数量|P'|大于种群数N,则先去除P'在znad外的解,并得到剩余解集P'和去除解集PE,再进行第二次判断,如果P'的数量|P'|仍然大于种群数N,则使用层次聚类方法来挑选下一代种群。第二次判断中,如果P'的数量|P'|小于种群数N,则根据PE中的解到z*的最短欧氏距离来挑选N-|P'|个解补充到P'。第一次判断中,如果P'的数量|P'|小于种群数N,则根据PR中的解到z*的最短欧氏距离来挑选N-|P'|个解补充到P'。最后返回一个新种群P',具体的实现细节可以参考算法2。 算法2:UpdatePop。 输入:N:种群数;PU:父代和子代的合并种群;SC:PU的角点解集;z*:近似的理想点;znad:近似的极值点。 输出:新种群P'。 1.获取PU的非支配解集P'和剩余解集PR; 2.if |P'|>Nthen 3.去除P'在znad外的解,得剩余解集P'和去除解集PE; 4.if |P'|>Nthen 5.P'=HCSelection(N,P',SC); 6.else 7.根据PE中的解到z*的欧氏距离挑选N-|P'|个解补充到P'; 8.end 9.else 10.根据PR中的解到z*的欧氏距离挑N-|P'|个解补充到P'; 11.end 12.returnP' 首先把PU的角点解集SC加入到新种群P,接下来使用层次聚类的方法挑选出剩下的N-|SC|个解加入到P中,|SC|表示角点解集的数量。 在层词聚类前先对每个解x∈P'的目标向量进行归一化,归一化的公式如下: (6) (7) 算法3:HCselection。 输入:N:种群数;P':候选种群;SC:PU的角点解集。 输出:新种群P。 1.P=∅; 2.P=P∪SC; 6.foreach idx∈Ido 8.按式(7)来计算聚类中心权重向量λidx; 11.P=P∪xB; 12.end 13.returnP MaF系列测试问题[11]是一组流行的超多目标优化问题。该文主要选择了MaF系列中前11个测试问题来检验MaOEA-ABHC与4个流行超多目标优化对比算法的性能,这些对比算法主要包括NSGA-II、MOEA/D-DE、RVEA和MaOEA/IGD。每个算法都独立地运行目标变量数m为5和10的MaF1-MaF11测试问题30次。在5目标的MaF中,除了MaF7的决策变量数n为24和MaF8-9的n为2外,其他问题的n都为14;在10目标的MaF中,除了MaF7的决策变量数n为29和MaF8-9的n为2外,其他问题的n都为19。所有算法的种群数都设为200,并且每个测试问题的最大目标函数评估次数都设为100 000次。 除了上文提到的IGD指标外,还有Hypervolume Indicator[12](HV)、IGD+[13]和R2[14]等评价指标。该文主要使用一种考虑收敛性和多样性的综合指标HV来评价所有算法的性能,以上算法都在PlatEMO[15]上实现,并使用PlatEMO自带的HV计算方法来计算所有算法的HV值。此外,还使用了置信度为0.05的Wilcoxon秩和检验来度量MaOEA-ABHC与其他对比算法的显著性,其中符号=表示MaOEA-ABHC和其他对比算法没有显著性区别,符号+和-分别表示MaOEA-ABHC明显地比其他对比算法好和差。 正如表1所示,MaOEA-ABHC在大多数测试问题上都取得了最佳的HV值,并且在大多数测试问题上,MaOEA-ABHC的算法性能都显著地优于其他对比算法。由于HV是一种考虑多样性和收敛性的综合指标,这表明MaOEA-ABHC在解决各类型的MaOP上都能保持较好的多样性和收敛性,并能有效地求解各类型的MaOP。 表1 所有算法在全部测试问题上的HV均值和显著性符号(每个问题的最佳指标值加粗显示) 许多工程优化问题都属于超多目标优化问题。由于目标空间过于庞大,并且算法往往只能使用规模较少的种群来近似问题的PF,这使得多数算法难以保持较好的收敛性和多样性。此外,许多算法往往忽视使用极值点的有用信息来帮助算法加速收敛并提升优化性能。在一个求角点解集方法的基础上,该文使用角点解集近似边界(极值点)并加速算法收敛,然后使用层次聚类进行选解来保证算法的收敛性和多样性。在未来,将进一步拓展算法来研究并求解一些实际应用问题。1.3 多目标优化算法研究综述
1.4 使用角点解近似理想点和极值点
1.5 研究动机
2 算法设计
2.1 算法框架
2.2 更新种群
2.3 层次聚类选解

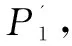



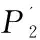
3 实验设计
3.1 实验参数设置
3.2 实验结果
4 结束语
