一种基于深度学习的无人机识别方法

黄湘鹏，黄晓刚

(海军装备部驻南京地区第四军事代表室，南京 211106)

0 引 言

在过去几年中，小型无人驾驶飞机的普及迅速发展，并且有望进一步增加。小型无人机在军事领域和民用领域都得到越来越广泛的应用，例如获得重要事件的电视录像或在危险地区提供急救支持。无人机在给人们生活带来便利的同时也对个人隐私、社会安全、军事安全等领域构成了严重威胁。[1-2]如何更快、更精确地实现无人机的检测和识别是无人机反制的前提，但小型无人机由于飞行速度较慢、飞行高度较低等原因很难被检测到。此外，飞鸟可能会导致无人机检测系统出现很多的虚警。因此，不仅必须及时检测进来的无人机，而且要将其归类为可疑的、具有潜在危险的人造目标。

一般来说，小型无人机的检测和识别可以使用不同的传感器执行，例如声学传感器、高分辨率红外传感器、光学传感器和雷达等。通常，通过声传感器进行的检测很不可靠，因为小型无人机相对安静，并且在城市中环境噪声水平一般较高。利用光学图像实现无人机检测和识别是一种常用手段。随着机器学习及深度学习技术的发展，越来越多的研究者选择构建深度学习网络实现无人机分类，在有足够训练资源的情况下可以达到较好的性能。[3]高分辨红外传感器能够在一定距离检测无人机，检测后可以通过放大目标区域以获得支持分类的详细图像。但是，红外传感器无法提供目标的速度和范围，既不适合大区域搜索也不适合雾天等恶劣天气条件下运行，而这些却是雷达的强项。国外有些研究者使用高重频雷达获取目标微多普勒特征，实现无人机分类。[4-6]本文聚焦于无人机与飞鸟的分类识别，提出一种基于深度学习的无人机识别方法。主要工作有：(1)构建深度学习网络，利用深度学习网络强大的学习能力，对目标RCS序列进行特征学习，获得特征向量后使用逻辑回归进行分类；(2)针对无人机数据远少于飞鸟数据量的问题，基于SMOTE(Synthetic Minority Over-sampling Technique)算法提出聚类SMOTE算法，一定程度上缓解了数据不平衡问题。通过实测数据验证，本文方法具有良好的分类性能，在无人机识别正确率达到87%的同时过滤掉60%的飞鸟目标。

1 处理流程

图1为无人机识别流程。首先由雷达回波提取目标RCS序列，训练集和测试集数据独立采集，可验证方法的有效性；然后对训练集和测试集数据分别进行预处理，本文采用均值方差归一化，测试集使用训练集的均值方差进行归一化；训练集数据由于存在数据不平衡的问题，使用聚类SMOTE算法插值平衡；使用平衡后的训练集训练深度学习网络，使用测试集验证训练好的深度神经网络。

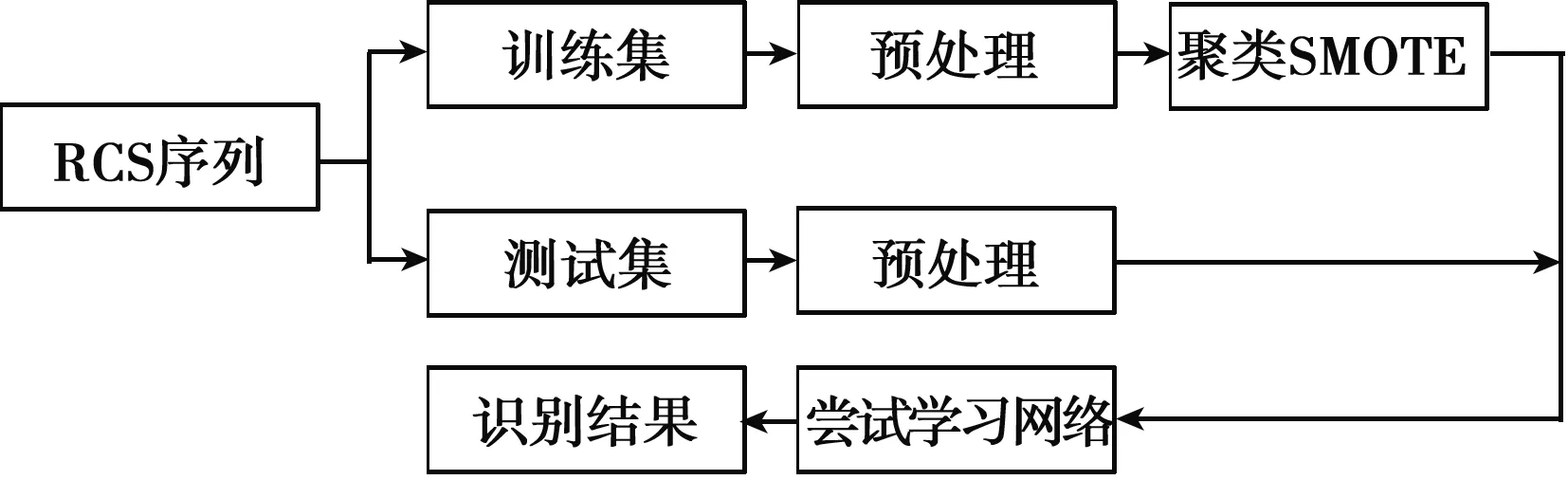
图1 无人机识别流程

2 深度学习网络

2.1 网络结构

本文的深度学习网络使用卷积神经网络搭建，有1个输入层、两个卷积层加池化层、1个全连接层和1个输出层。卷积核大小为3*1。卷积层及全连接层激活函数均为ReLU函数。第2层卷积层及全连接层接dropout，随机失活一半的神经元，以缓解过拟合现象。训练时训练集数据批量输入，大小为N*12*1(其中N为批大小，12为序列长度，1为通道数)。经过第1层卷积后输出特征图大小为N*12*32，经过池化后特征图大小为N*6*32。第2层卷积后输出特征图大小为N*6*64，经过池化后特征图大小为N*3*64。全连接层输出128维特征向量，输出层输出目标为无人机的置信度，越接近1则无人机的置信度越高。图2为无人机识别网络结构。

图2 无人机识别网络结构

2.2 卷积神经网络

卷积神经网络是深度学习模型中的重要内容。[7]在传统人工神经网络中引用了卷积核、池化层等操作，实现了权值共享，具有强大的特征提取能力，并且相对于全连接网络有效减少了网络参数，在一定程度上缓解了过拟合，提升了网络的性能。

卷积神经网络由输入层、输出层及多个隐藏层构成。隐藏层一般包括卷积层、池化层。池化层接在卷积层后面，减少特征维数。输入样本在输入后首先经过卷积层，与卷积核进行卷积，然后加上偏置。经过卷积后输出的特征向量再输入池化层进行特征降维。一般网络中有多个卷积层和池化层。卷积层的输出作为池化层的输入，池化层的输出作为下一层卷积的输入。重复上述的卷积池化操作，直至达到设定的网络深度。在卷积和池化操作后，输出的特征向量一般会使用非线性激活函数激活映射成非线性特征。卷积神经网络的最后一层或几层一般是全连接层。全连接层的作用是对卷积结构提取的抽象特征进行合并整合。在网络末尾通常会连接着logistic回归或softmax分类器，实现二分类或者多分类。

2.3 卷积神经网络训练

和其他的人工神经网络类似，卷积神经网络的训练过程通常分为前向传播和后向传播两个主要过程。[8]前向传播表达了特征信息的传递。反向传播主要是传播误差，计算梯度通过梯度下降方法实现参数的更新，并使参数最终收敛至全局最小或局部最先值。

(1) 前向传播

全连接层前向传播公式可以表示为

al=σ(al-1wl+bl)

(1)

其中，σ()为非线性激活函数，一般有Sigmoid、tanh、ReLU等。

卷积层的前向传播公式可表示为

al=σ(al-1*wl+bl)

(2)

池化层是对卷积得到的特征图进行下采样的过程，主要有平均池化、最大池化等方式。

(2) 后向传播

• 最后一层的残差

(3)

δL=▽aCeσ′(zL)

(4)

• 全连接层残差反向传播公式

δl=((wl+1)Tδl+1)·σ′(zl)

(5)

• 全连接层权重及偏置更新公式

(6)

(7)

• 卷积层残差反向传播公式

δl=δl+1*rot180(wl+1)·σ′(zl)

(8)

• 卷积层权重及偏置更新公式

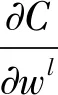
(9)

(10)

池化层残差反向传播时，如果是最大池化层，则下一层的误差项的值会原封不动地传递到上一层对应区块中的最大值所对应的神经元，而其他神经元的误差项的值都为零。如果是平均池化层，下一层的误差项会平均分配到上一层对应区块中的所有神经元。

3 聚类SMOTE算法

在进行鸟和无人机的数据处理时，由于鸟类数据多，无人机数据少，鸟类样本是无人机样本的好几倍，数据集存在严重的不平衡问题，因此可能会导致模型学到的分类决策面倾向鸟类一侧，导致无人机分裂损失过大，无法有效识别无人机。数据集不平衡问题是机器学习中经常遇到的一类问题。在不平衡问题中一般将样本多的类称为多数类，样本少的类称为少数类。在像本文的这种二分类问题中，将多数类称为负类，少数类称为正类。由于样本数量的严重倾斜，直接分类具有很大的偏向性。多数类的分类准确率相对较高，少数类的分类准确率相对较低。不均衡数据的分类问题是机器学习、深度学习领域的重要研究内容之一，在均衡数据集上表现良好的分类方法在不均衡数据集上往往会暴露出很多问题。常用的解决方法主要分为两个层面：数据层面和算法层面。数据层面包括上采样、下采样和混合采样，算法层面主要包括单类学习、集成学习、代价敏感性学习等方法，目前比较常用的方法是SMOTE算法。[9]

3.1 SMOTE算法

SMOTE算法是一种过采样算法，被广泛应用于解决不平衡数据集的问题，其主要思想是：对于每一个少数类样本x，搜索其K个同类最近邻样本，若上采样的倍率是N，则在其K个最近邻样本中随机选择N个样本，记为y1,y2,…,yN，在少数类样本x和yi(i=1,2,…,N)之间进行随机线性插值，构造新的少数类样本pi。公式描述如下：

pi=x+rand(0,1)*(yi-x),i=1,2,…,N

(11)

在使用公式(11)插值后，将新产生的少数类样本加入到原来的训练集中产生新的训练集。

3.2 基于聚类的SMOTE

由图3可以看出，由于未考虑少数类内间聚类问题，直接插值会产生噪声，导致分类性能下降。因此，本文提出一种基于聚类的SMOTE算法，其基本思想是先利用K-means算法在少数类内部产生聚类，然后围绕类中心使用SMOTE算法插值。具体步骤如下：

(1) 统计杂波点数M、目标点数N(M>N)；

(2) 基于ENN(Edited Nearest Neighbor)，清理杂波噪声点，假设有P点；

(3) 利用T-SNE对目标数据可视化，得到目标类间聚类数C；

(4) 基于K-means对目标进行聚类，聚类数设为C，聚类产生C个类间簇；

(5) 对每个类间簇使用SMOTE插值，每个点插值个数为(M-N-P)/N。

图3 SMOTE插值

4 分类性能评价指标

由于类别不平衡，不能简单地使用平均准确率作为评价指标，因为多数类样本对平均准确率的影响更大，性能评估度量应区别对待不同类别上的准确率，最常见的评价指标有F-measure、G-mean、AUC[10]等。为了介绍这些指标，先要引入模糊矩阵这一概念，如表1所示。

表1 混淆矩阵

TP表示实际为正例被分为正例的样本数，同理FN、FP、TN分别表示对应情况的样本数，显然有TP+FN+FP+TN=样本总数。精准度是分类问题常用的评价指标，在样本平衡时可以有效地反映分类器的分类性能。

(12)

针对不平衡数据集，常用的评价指标有F-measure、G-mean、ROC曲线和AUC。

(13)

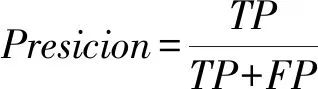
(14)

可以看出，G-mean值综合考虑了两类的分类准确率，相对于单独使用准确率而言，能够更好地衡量分类器的分类性能，不均衡数据集下常用的衡量指标。

在本文中，分类器采用卷积神经网络，网络末尾使用logistic回归输出样本是无人机的置信度。实际上，可以设置一系列置信度阈值，大于阈值则认为是正类(无人机)，小于阈值则认为是负类(鸟)。因此，可以得到一个动态的指标。一般将“真正类率”(TPR)作为纵轴，“假正类率”(FPR)作为横轴，得到的曲线称为ROC曲线。TPR和FPR定义为

(15)

(16)

一般来说，ROC曲线越靠近左上角说明分类器性能越好。为了定量地比较，可以ROC曲线下的面积，也就是AUC值，AUC值越大则说明分类器性能越好。本文综合使用这几个指标来评价无人机的分类性能。

5 实录数据验证

5.1 数据集

训练集和测试集来自不同日期、不同批次的数据。因此，测试集可有效验证方法的泛化能力。从表2可以看出，数据集存在严重的不平衡问题，训练集中不平衡比例达到了8.36。因此，在训练前使用聚类插值方法将无人机样本从544个扩充到4 548个。实验中也使用了未平衡的原始数据训练作为对照比较。

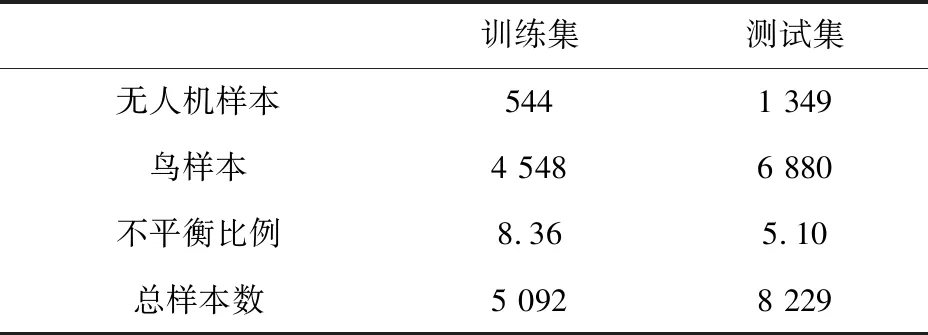
表2 数据集

在数据输入网络前需要对数据预处理，将数据缩放在0～1间。无人机和鸟样本示例如图4所示。

5.2 训练过程及特征可视化

在训练中，随着训练的进行，训练损失会逐渐降低，网络会慢慢收敛，测试集的AUC值会逐渐上升。图5为训练集损失曲线，图6为测试集AUC变化曲线。

训练好的神经网络最后一层全连接层输出网络学习到的特征向量(如图7所示)，分别为鸟类样本和无人机类样本对应的特征向量。为了验证学习到的特征向量具有有效的可分性，使用PCA降维可视化(如图8所示)，可以看出数据在学习到的特征上具有明显的可分性。

图4 数据集样本

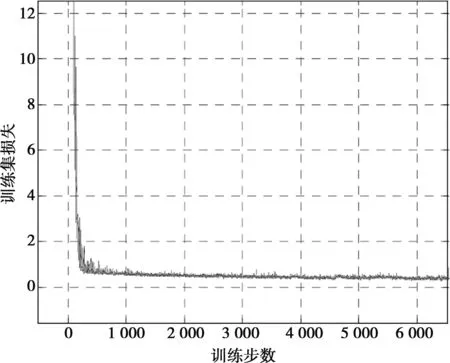
图5 训练集损失曲线

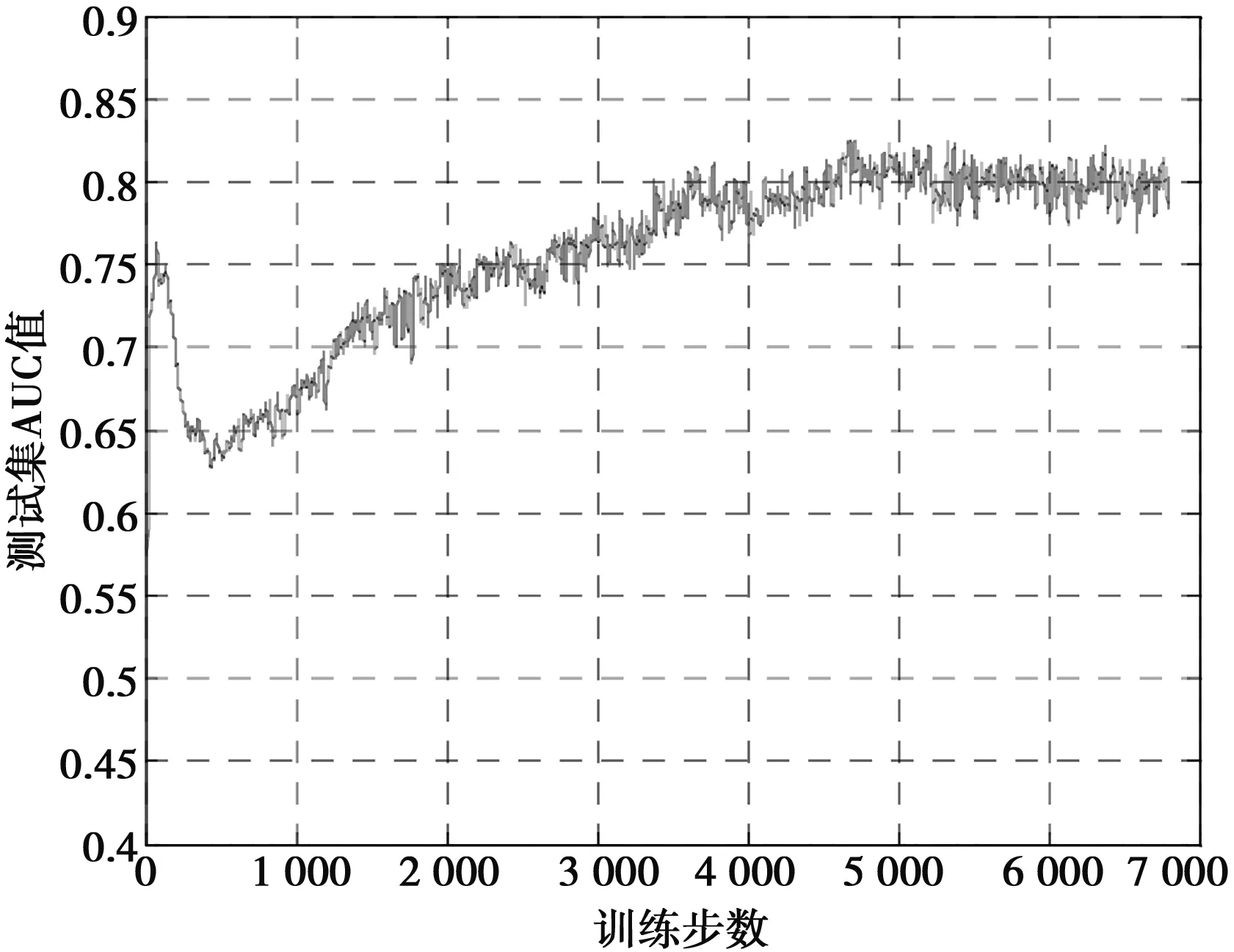
图6 测试集AUC变化曲线

图7 特征向量

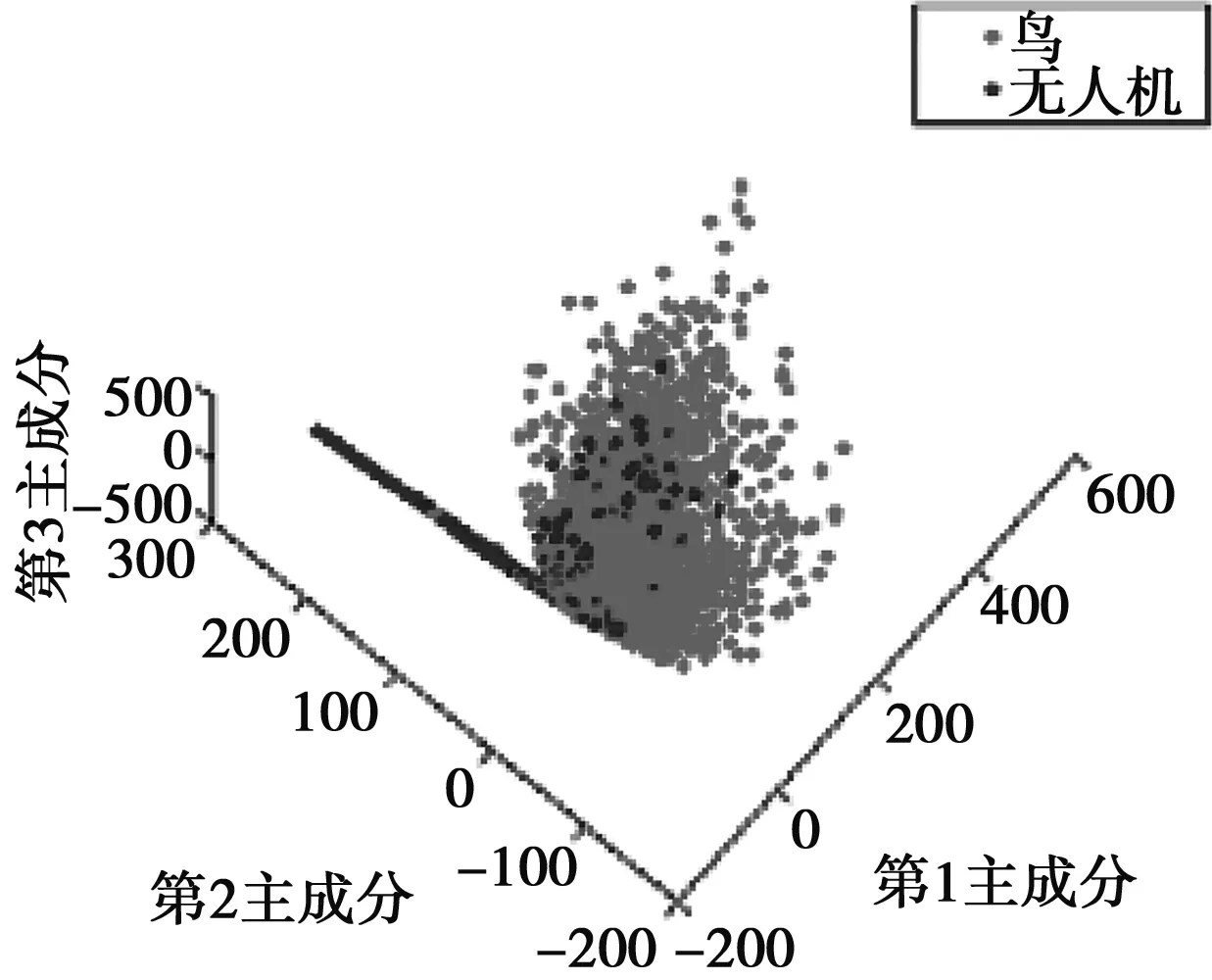
图8 特征向量可视化结果

5.3 性能分析

为了验证本文方法的有效性，采用F-measure、G-mean、ROC曲线、AUC 4个指标评价最终性能，并将使用SMOTE平衡的训练集和未平衡的训练集作为对照组，验证聚类SMOTE解决本文不平衡问题的能力。由表3可以看出，聚类SMOTE方法3种定量指标值均优于对照组，且由图9通过ROC曲线可以看出聚类SMOTE的 ROC曲线完全包裹住对照组曲线。实验结果可以看出，聚类SMOTE可有效缓解数据不平衡问题。将置信度阈值设为0.5后得到混淆矩阵如表4。可以看出，在无人机识别率达到87%的同时可过滤60%的虚假目标。

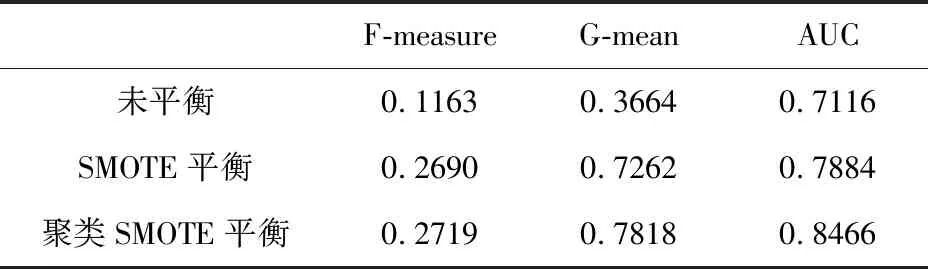
表3 指标对比

表4 混淆矩阵

6 结束语

由于小型无人机飞行速度较慢、飞行高度较低且RCS小，飞鸟会导致无人机检测系统出现大量虚警。本文聚焦于无人机和飞鸟的识别问题，使用深度学习网络对RCS序列进行特征学习，针对数据不平衡问题提出聚类SMOTE算法，进而实现无人机的有效识别。经过实录数据验证，本文方法在无人机识别准确率达到87%的同时过滤掉60%的飞鸟目标。