直驱两轴伺服转台实现
2020-12-25徐非骏
徐非骏,王 贺
(中国电子科技集团公司第三十八研究所,合肥 230088)
0 引 言
伺服转台常运用于军事和工业场合。转台控制器按照总控单元指令引导天线精确指向或跟踪目标,实时反馈天线的指向角度和状态信息。[1-2]伺服转台主要性能指标是承载质量、运动速度、运动加速度及跟踪精度。对于在一定负载下的伺服转台,如何在较大速度和加速度情况下实现更高跟踪精度一直是伺服转台追求的目标。
本文对某型伺服转台技术要求分析后决定采用直驱电机同轴安装实现转台驱动形式,对伺服转台结构形式及实现进行强度仿真,优化结构设计,建立有限元模型进行动态仿真验证并优化结构强度。为了实现控制上高响应的要求,自主研发以DSP为核心控制芯片的主控制器,进行运动算法的高速计算,结合FPGA实现角度数据和通讯的高速采集,再将计算后的对电机驱动控制信号传输给电机驱动器实现闭环控制。在控制器上通过对不同运动算法的改进,最终实现该类转台的技术指标要求。
1 结构总体设计
本设计转台结构形式采用方位-俯仰型,驱动电机采用电机同轴直驱,方位和俯仰转轴各安装一台旋转变压器和失电制动器。同轴直驱可以避免减速机及齿轮传动带来的齿隙误差,而且同轴驱动动态响应较高,适用于对动态性能要求较高的场合使用。转动轴上安装的旋转变压器模拟信号传送给轴角采集单元进行角度数字转换。同轴安装旋转变压器形式提高了检测角度的精度。
伺服转台台体采用铝合金低压铸造,为了保证结构刚性、强度及质量要求,通过有限元计算后进行迭代优化设计。伺服转台结构模型如图1所示。伺服转台的器件组成如图2所示。
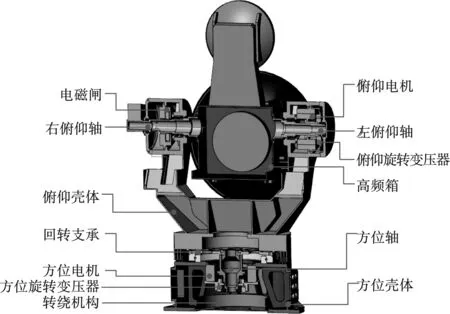
图1 转台外形结构
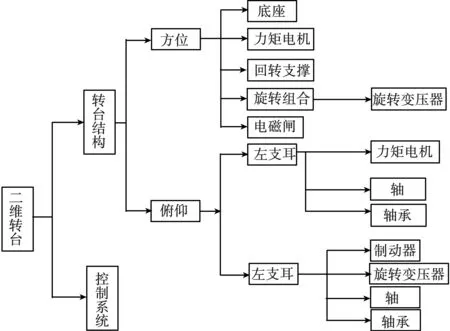
图2 两轴转台组成
本设计采用直驱电机驱动形式。直驱电机驱动即是电机直接驱动转动轴,而不是通过减速机齿轮捏合带动转动轴转动。电机分为动圈和定圈。动圈安装在转台转轴上。转轴上设计有定位法兰。转轴定位法兰安装电机动圈安装盘。电机动圈安装在电机动圈安装盘上。转轴定圈通过转台壳体上设计的法兰盘安装在转台壳体上。在转轴上还需要安装旋转变压器,用来检测转台转动角度。旋转变压器也采用同轴安装方式,其安装方式同直驱电机。动圈安装在转动轴上,而定圈安装在状态壳体上。本设计中电机安装在转轴最上部,采用将转轴在外部先与电机动圈安装完毕,再将转轴连同电机动圈安装入转台。转轴顶部通过法兰盘连接回转支撑动圈,然后通过工装安装入电机定子、旋转变压器动圈、旋转变压器定圈。转轴中后端再安装一个轴承,防止转轴远端摆动。由于直驱电机不带自锁功能,在失电状态下电机是自由转动状态,为了设备安全需要安装失电制动器确保转台在失电运输状态转台不会发生意外转动。本设计中,为了降低功率、减轻质量,选用一个小型化直流失电制动器。制动器输出轴安装一个齿轮。制动器输出齿轮和转台转轴上安装齿轮捏合转台转动轴安装的大齿轮,通过齿轮捏合及速比关系将制动器的锁定力矩放大进行失电以后转台锁定。转轴顶端通过预先设计在转轴上法兰孔安装过渡盘和回转支撑。回转支撑上安装俯仰转台。
同轴驱动电机和分装同轴旋转变压器对结构安装同轴度要求很高。除了设计时对同轴度进行设计保证,在加工时精度必须要按照图纸精度要求进行检测,且安装完毕后需要对转轴同轴度进行测量。一旦发现同轴度超出旋转变压器和电机要求的同轴度误差必须查找原因,直到同轴度满足要求才可以进行下一步工作。
直驱电机在电机定子上引出导线。旋转变压器定子和转子上都有引出线。本设计在转轴上预开一个走线孔,可以将旋转变压器转子的线从轴上走线孔引入到轴中空出,从转轴下部引出导线埋放在走线机构中。走线机构放置在方位转台底部,并根据需要安排电缆数量进行粗细选择。本设计转台由于不要进行连续旋转,走线机构只需要在转动范围内提前设计好转动范围即可。方位转台转动时,走线机构带动线槽内电缆在转台底部按照设计好范围转动。具体方位结构如图3所示。

图3 方位转台结构
俯仰结构将电机和旋转变压器安装在俯仰转台支耳同一侧。俯仰转台支耳另一侧安装失电制动器,两侧转轴通过俯仰背箱连接。鉴于篇幅限制,不再展开详述。
伺服转台台体结构框架是整个伺服系统动态性能指标的保证和系统安全性的保障。对伺服转台的结构必须进行力学仿真,通过对转台的模态分析以校核验证转台在结构强度及振动状态下安全性。
结合转台机械结构设计,并分析转台结构特点,对转台的轴承、电机等复杂件进行简化和等效处理,施加载荷,选择了实际边界条件,建立了转台的有限元模型。动态分析时,根据转台模态分析振型,分析得出转台的刚度薄弱部位。针对分析结果,对结构进行了优化设计,并对优化结果进行分析计算,确保优化方案有效。[3]由于篇幅限制,只给出转台有限元分析图的1阶和2阶。
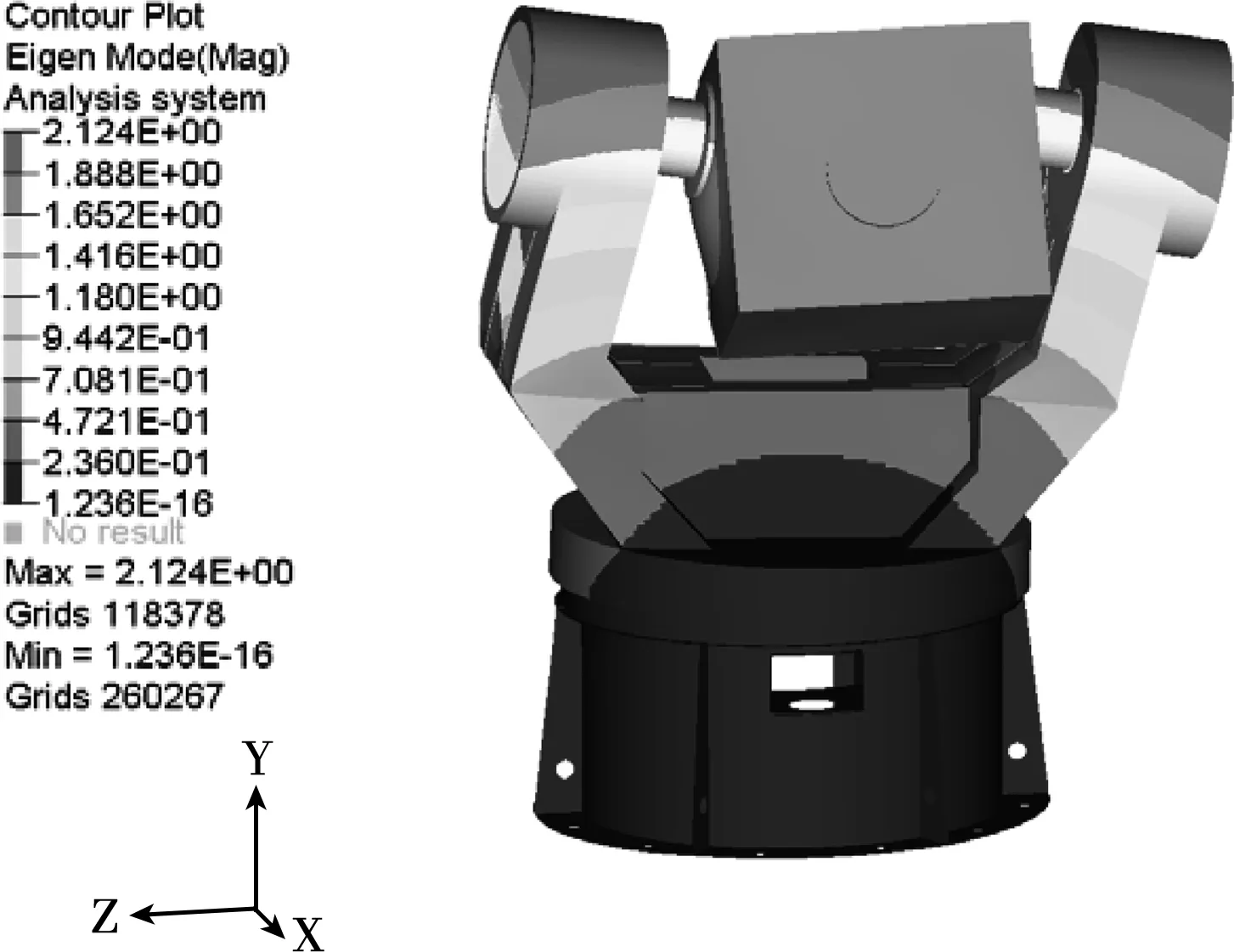
图4 一阶模态振型
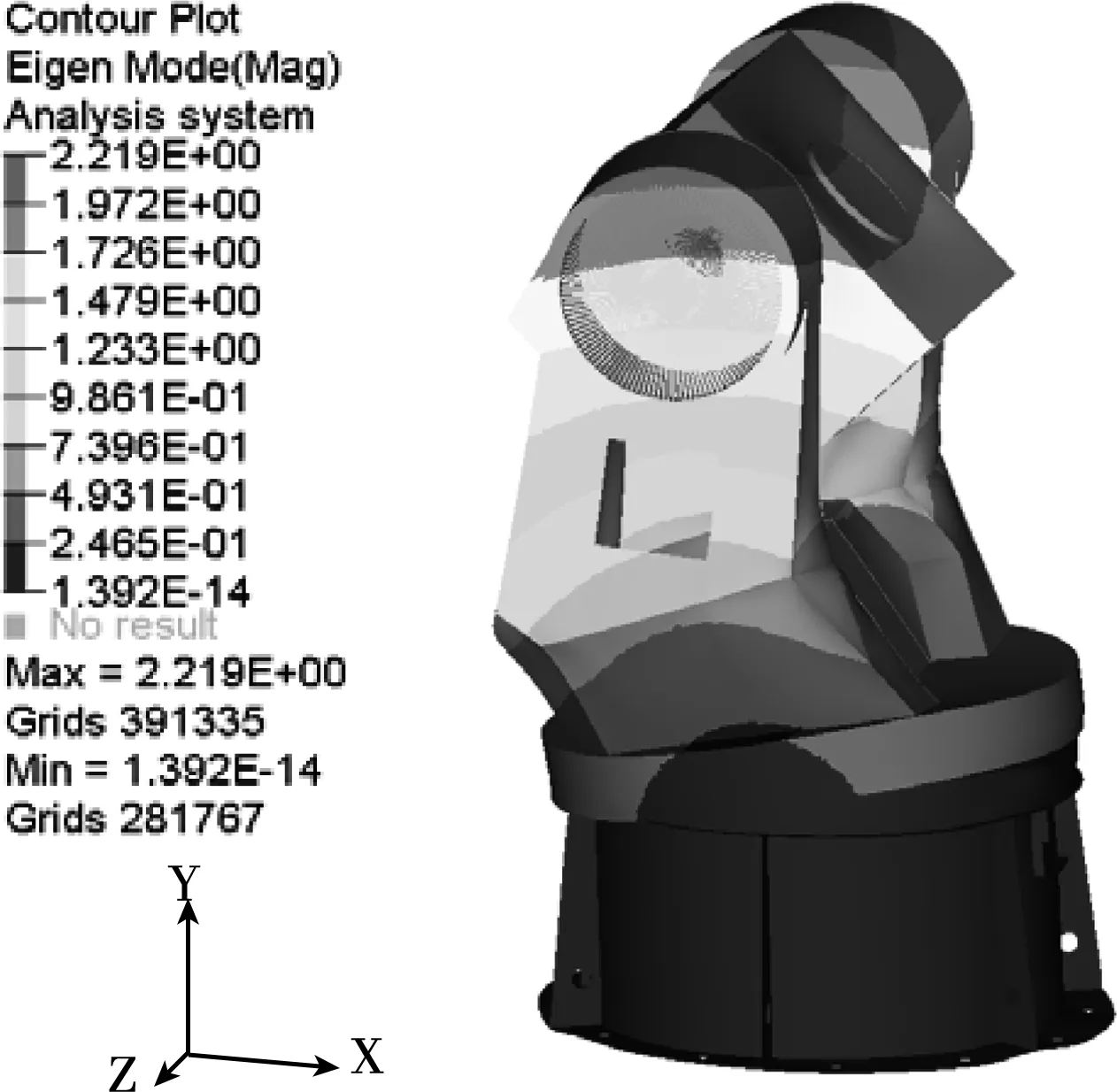
图5 二阶模态振型
模态分析结果如表1所示。从表1可以看出,转台俯仰向摆动模态频率为49.7 Hz,方位向扭转模态频率为67.9 Hz,满足结构设计动刚度要求。

表1 模态分析结果
2 伺服控制系统设计
伺服控制核心是伺服控制器。伺服控制器根据总控控制指令,结合采集的旋转变压器的角度信号,通过控制算法得到速度指令,将速度指令发送给电机驱动器驱动电机转动,并且将当前伺服系统状态发送给上位机。[4]伺服控制系统组成框图如图6所示。
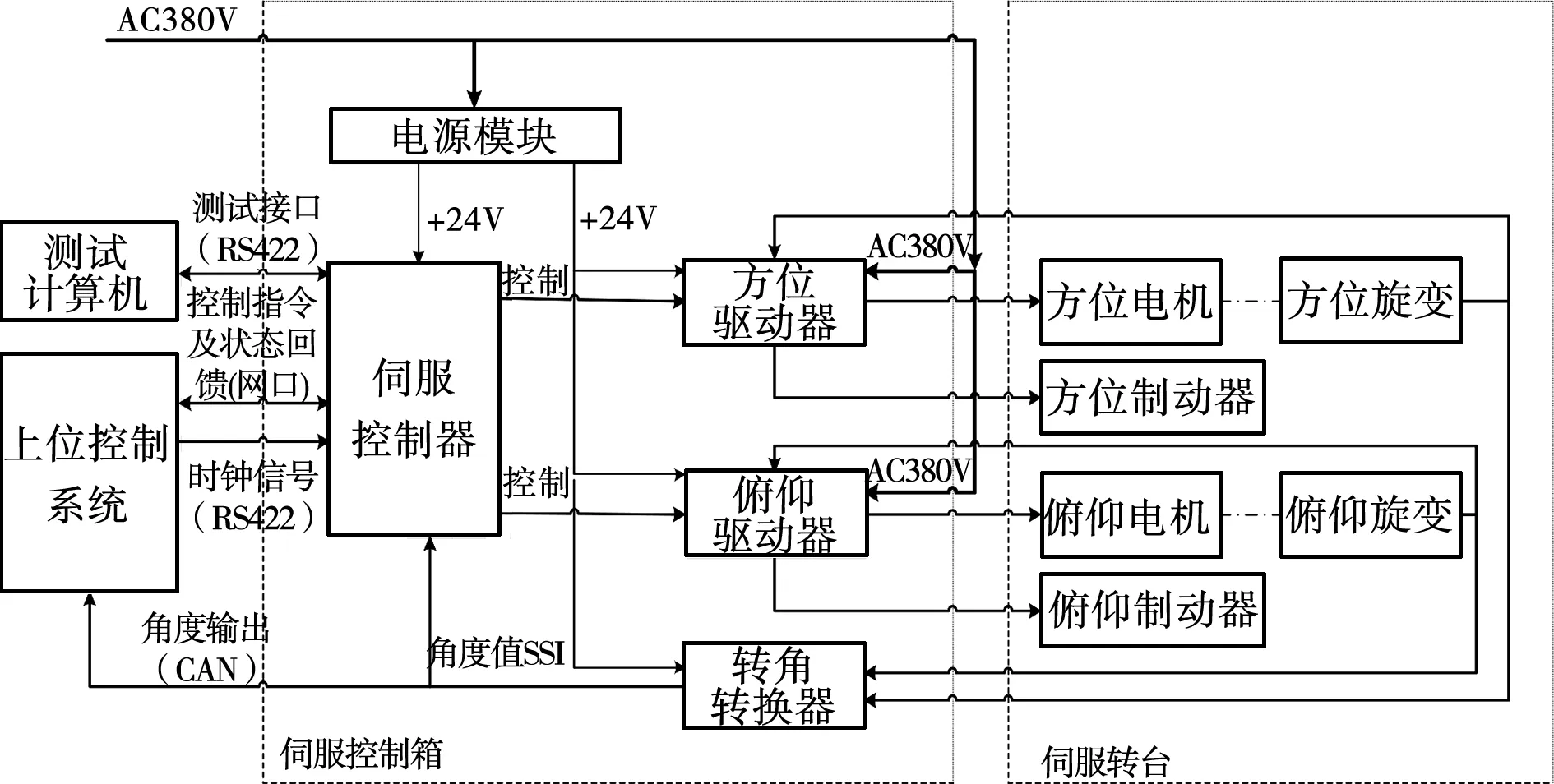
图6 伺服控制系统组成框图
2.1 伺服控制器设计
按照技术指标和功能需求,伺服系统对伺服控制器提出高精度控制及高稳定性的要求。本设计采用 DSP+FPGA 平台作为算法运行及信号采集,并在此平台基础上设计了伺服控制系统软硬件方案。[5]
本方案中伺服控制器采用高性能浮点DSP 芯片TMS320F28335作为控制和运算核心完成伺服功能。为了避免串口噪声和串口高频率的接收和发送对伺服系统性能产生影响,使用 FPGA 完成核心 DSP 与外围器件的数据交互。方位控制器和俯仰控制器之间采用CAN 通信方式。方位控制器和监控系统通过网络转换芯片实现UDP网络通信方式。[6]伺服控制器组成框图见图7。
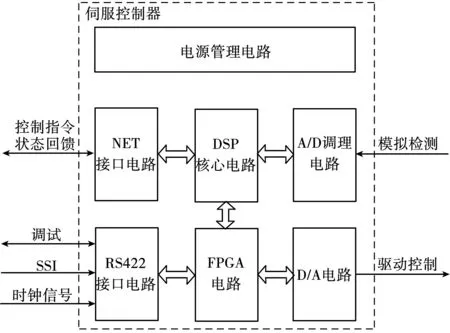
图7 伺服控制器组成框图
旋转编码器的角度采集采用杰瑞电子的模块化一体轴角解码盒,能够输出相应的激磁电源及对两路双通道旋转变压器进行角度解算。该器件 20 位的高精度能够将解码误差限制在 4″以内。
伺服控制器和轴角解码盒均采用金属外壳安装方式,有利于增强伺服控制箱内复杂电磁环境下的控制器和轴角解算的抗干扰能力。
2.2 伺服控制方法
本系统采用传统的电流环、速度环、位置环的三环控制模型,其电流环和速度环的实现在驱动器上实现。具体控制方法采用PI控制方法,通过驱动器上相应的PI参数调整,对伺服控制转台的方位轴和俯仰轴进行阶跃响应的调整。首先调试电流环,其后是调整速度环。以上两个环路调整完毕后,对最外环的位置环进行调试。本文主要介绍位置环的实现方法。位置环在DSP控制器上实现,控制方法采用模糊自适应PID控制方法。模糊自适应PID控制是在PID算法的基础上,以误差e和误差变化率ec作为输入,利用模糊规则进行模糊推理,查询模糊矩阵表进行参数调整,来满足不同时刻的e和ec对PID参数自整定的要求[7],克服了传统PID控制方法的精度低、抗干扰能力差等缺点。[8]
PID控制是一种线性控制。它根据该定值r(t)与实际输出值y(t)构成控制偏差e(t)=r(t)-y(t)。连续情况如公式(1):
(1)
对公式(1)进行离散化,离散后如公式(2)和公式(3):
(2)
Δu(k)=kp(e(k)-e(k-1))+kie(k)+
kd(e(k)-2e(k-1)+e(k-2))
(3)
用于参数调整的模糊控制器采用二输入三输出的形式。该控制器是以误差e和误差变化率ec作为输入,PID控制器的3个参数P、I、D的修正Δkp,Δki,Δkd作为输出。取输入误差e和误差变化率ec及输出Δkp,Δki,Δkd模糊子集为{NB,NM,NS,ZO,PS,PM,PB},子集中元素分别代表负大、负中、负小、零、正小、正中、正大。误差e和误差变化率ec的论域为[-3,3],量化等级为{-3,-2,-1,0,1,2,3}。
根据各模糊子集的隶属度赋值表和各参数模糊控制模型,应用模糊合成推理设计分数阶PID参数的模糊矩阵表,算出参数代入公式(4)、(5)和(6):
kp=kp0+Δkp
(4)
ki=ki0+Δki
(5)
kd=kd0+Δkd
(6)
式中,kp0,ki0,kd0为PID参数的初始设计值,由常规的PID控制器的参数整定方法设计;Δkp,Δki,Δkd为模糊控制器的3个输出,可根据被控对象的状态自动调整PID控制参数的取值。[9]
2.3 伺服带宽设计和伺服精度仿真
将指标要求的角速度和角加速度指标等效为正弦输入信号,并将此信号作为伺服控制系统的跟踪精度检验信号。
根据系统指标要求:
计算得到精度检测点(等效正弦)频率:
等效正弦幅值:
等效正弦信号:
θ(t)=Asin(ωt)=83.3sin(1.2t)
在伺服转台结构设计中,转台台体要有相应的结构强度来满足各种负载加速度等要求,且随着转台台体质量增加其结构谐振频率会降低, 限制系统的动态响应能力。因此,对转台建模也是转台伺服系统仿真的一个重要环节。
本设计转台跟踪精度仿真使用AMESim软件。控制器设计为模糊PID控制器+速度前馈的控制器。综合轴角测量误差、风力矩和摩擦力矩,建立的方位轴仿真模型如图8所示。
图8中,等效跟踪曲线为幅值83.3°的正弦信号,取旋转变压器测角误差为20 s(即0.0056°),根据工程经验取风力矩为73 Nm,摩擦力矩55 Nm。控制器参数如表2所示。

表2 控制器仿真参数
按照该条件从位置环进行输入,然后记录控制器采集的当前的角度信号,得到角度跟踪曲线和位置误差曲线如图9所示。
俯仰轴仿真方法同方位轴,只是控制器仿真参数设置不同,经过仿真得到图10仿真曲线。
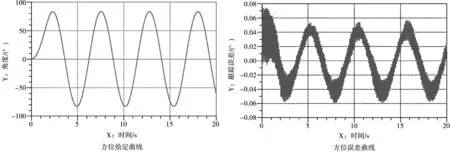
图9 方位误差曲线
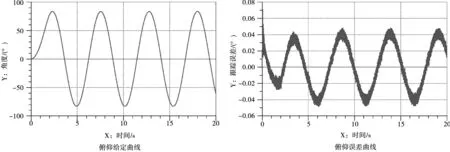
图10 俯仰误差曲线
3 测试结果
在实际测试中,通过对伺服转台控制器串口输入引导角度信息,模拟上位机发送引导数据。引导角度数据根据公式(7):
θ=ε0+Asin(ω×t)
(7)
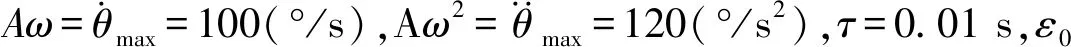
伺服控制器从旋转变压器转换模块进行转台方位轴和俯仰轴角度位置采集,采样周期1 ms,然后与给定位置信号进行比较得出误差,测试结果如图11、12、13、14所示。经过测试,方位轴和俯仰轴在指标要求跟踪速度和加速度情况下达到跟踪误差小于0.056°。
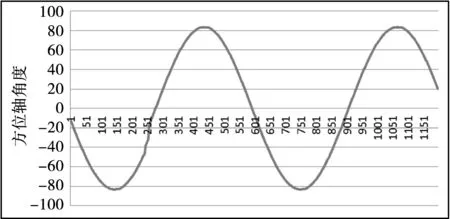
图11 方位轴给定角度曲线
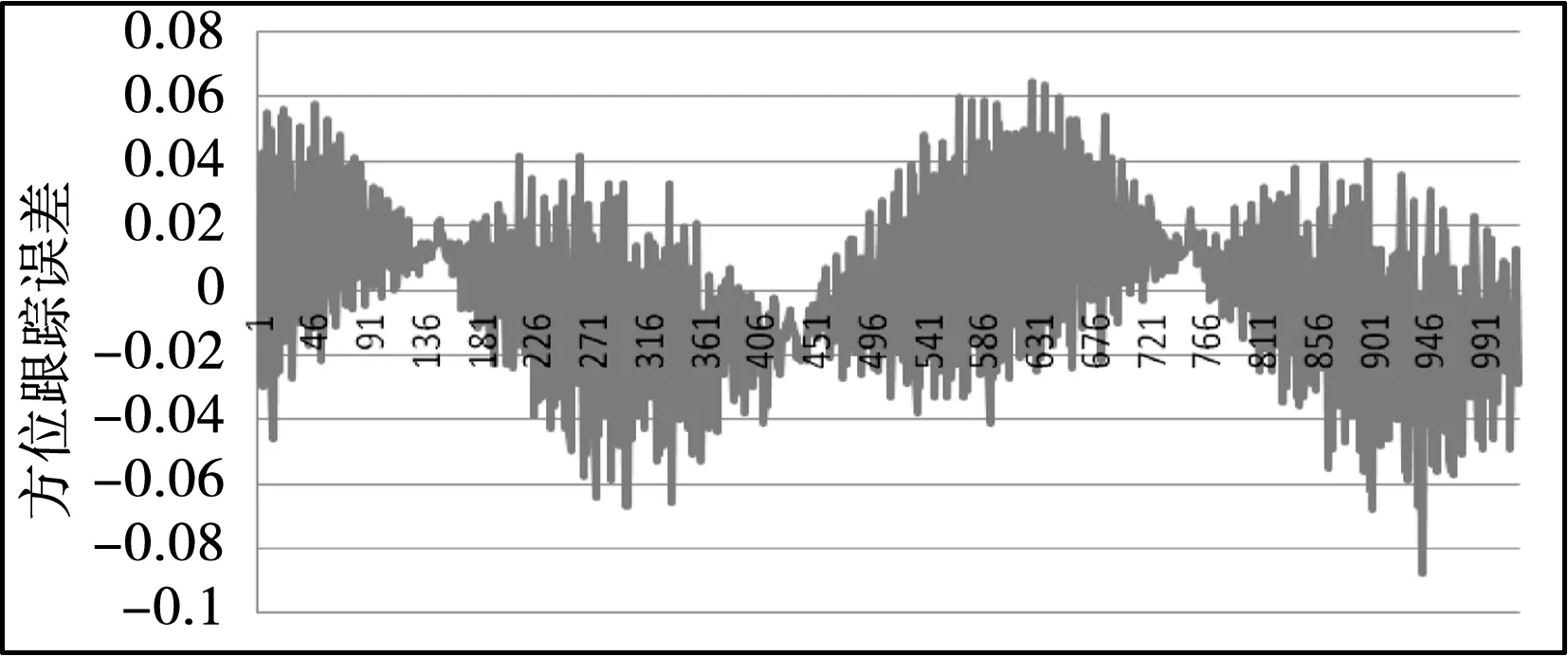
图12 方位轴跟踪误差实测曲线
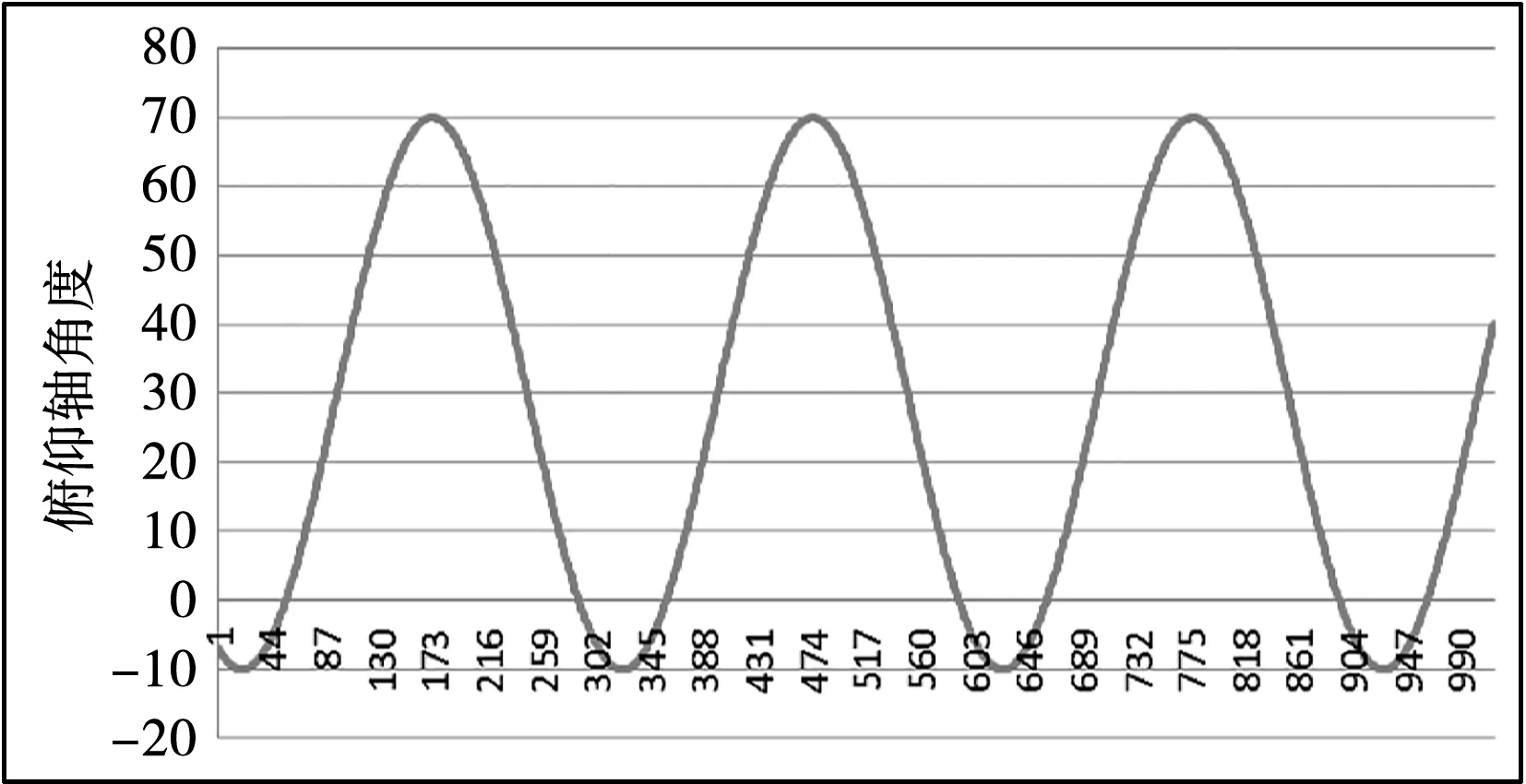
图13 俯仰轴给定角度曲线
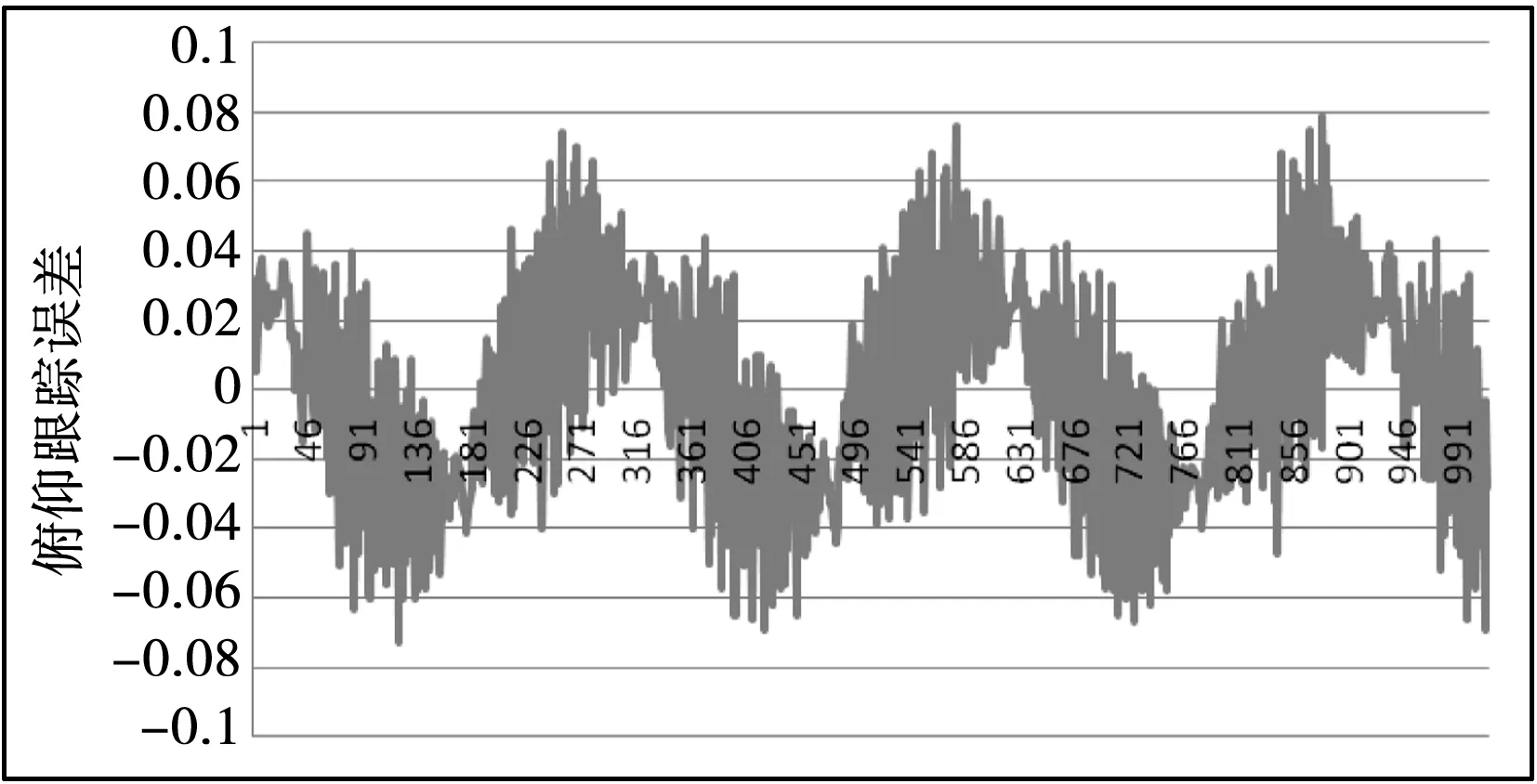
图14 俯仰轴跟踪误差实测曲线
4 结束语
本文对直驱两轴伺服转台结构组成、转台力学仿真、伺服控制系统组成、伺服控制器的设计和伺服仿真几个方面对本伺服转台设计进行了阐述,采用本文描述的方法设计出样机一台,并且进行了详细的静态测试及动态测试。目前,该转台已经交付用户,使用效果良好。
