考虑载荷不确定性的转向节结构优化研究*
2020-12-24陈天赋
刘 莹,晏 洋,陈天赋,庞 秋
(1.武汉理工大学 现代汽车零部件技术湖北省重点实验室,湖北 武汉 430070;2.汽车零部件技术湖北协同创新中心,湖北 武汉 430070;3.湖北三环锻造有限公司湖北 襄阳 441700;4.武汉东湖学院 机电工程学院,湖北 武汉 430212)
0 前 言
转向节是转向系统的执行构件,在工作过程中承受多种载荷,若设计不当会出现断轴等危险,因此对其安全性要求高[1]。
为了得到转向节的静力分析结果,笔者需要建立双叉臂悬架的多体动力学模型,并选取3种典型工况进行轮胎接地力计算,以得到转向节关键点载荷;然后通过有限元分析方法进行强度分析,最后利用拓扑优化进行减重设计。
针对多变量优化中设计变量的选取问题,目前常用的方法有因子筛选法[2]、基于方差的灵敏度分析法[3]、相关系数法[4]、矩独立法[5]等方法。为减少实验次数,提高筛选效率,可在无重复正交饱和试验设计的基础上,利用零效应搜索法进行因子筛选。
在优化设计中,某些不确定性因素不可避免地存在,如材料属性[6]、尺寸公差[7]、边界条件[8]等。对转向节而言,由于其工作条件的复杂性,在优化设计中应考虑载荷不确定性对转向节最大应力的影响。而转向节所受载荷概率分布并不能提前预知,因此需要利用区间不确定性分析优化方法进行转向节的优化。
笔者在建立悬架多体动力学模型的基础上得到转向节关键点的载荷,以此作为边界条件对转向节进行有限元分析,并在结构优化过程中考虑区间不确定性,在保证结构性能的基础上实现转向节的轻量化设计。
1 转向节有限元模型建立
1.1 典型工况载荷获取
笔者在CATIA中对双叉臂悬架模型进行测量,得到悬架运动学参数(硬点坐标等)、动力学参数(质心、转动惯量)等参数,在Adams/car中建立双叉臂悬架的多体动力学模型,同时根据整车相关参数,选取0.4 g转向、越过不平路面、0.6 g紧急制动3种典型工况进行仿真,将计算得到的接地力作为输入,得到转向节硬点处的载荷如表1所示。
1.2 网格划分
笔者将转向节进行简化,去除倒角以及小凸台等特征,从而提高网格划分质量,然后将其导入ANSYS中进行网格划分,采用单元类型为solid92。转向节材料为6 082铝合金,泊松比取0.33,弹性模量为70 GPa,密度为2.7e-9 t/mm3。
1.3 强度分析
笔者利用惯性释放法,在ANSYS中进行有限元模拟,得到的强度分析结果如图1所示。
通过图1的应力云图可知,应力较大区域主要集中在转向节长臂处,0.4 g转向最大应力值为181 MPa,越过不平路面最大应力值为167.3 MPa,0.6 g紧急制动的最大应力108 MPa。
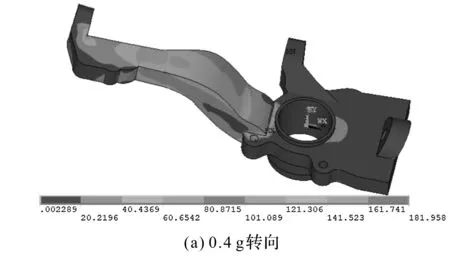

图1 3种工况下应力分布
2 拓扑优化
拓扑优化是在设计区域寻找最佳材料分布,以最少的材料获得最佳结构性能的优化方法[9]。其数学模型如下所示:
(1)
式中:C(ρ)—以密度ρ为设计变量的柔度函数;ωi—3种工况下的权重;Ci(ρ)—迭代次数为i时的柔度值;(V(ρ)-V0)—第i次迭代的体积V(ρ)与初始体积V0之差。
取0.4 g转向、越过不平路面、0.6 g紧急制动3种工况下的权重大小为0.4,0.3,0.3,在ANSYS中进行拓扑优化计算,经过迭代得到的优化结果如图2所示。

图2 拓扑优化结果
由图2可知,主要优化区域位于转向节下半部分。
考虑转向节与其他部件的配合问题,各圆柱孔处应保留原有结构,考虑强度及可制造性因素,转向拉杆处材料保留,最终得到的优化结果如图3所示。

图3 转向节改进后结构
笔者对拓扑优化后结果进行强度分析,优化前后的对比结果如表2所示。

表2 优化前、后各工况下应力大小
由表2可知,由于部分结构的去除导致应力值有所上升,为此笔者选取应力值最大的0.4 g转向工况对转向节进行形状优化。
3 基于零效应搜索法的因子筛选
3.1 设计变量的选取
转向节0.4 g转向的强度分析结果如图4所示。

图4 拓扑优化后0.4 g转向应力分析
由图4的应力云图可知,应力主要集中在转向节长臂处,且文献[10]也指出,转向节疲劳破坏常发生在长臂处。
为此,笔者选取长臂处的11个参数为设计变量,其示意图如图5所示。

图5 转向节控制参数
取各点之间的半径为控制参数,其命名规则,即两点之间的半径,设计变量及初值、上下限如表3所示。

表3 控制参数及其变化范围
重复正交饱和析因设计主要是研究N个因子的N+1次实验的多水平分式析因设计。由于没有多余的试验次数进行误差平方和检验,基于显著因子只占少部分的假设,而提出一系列显著性检验的方法:半正态概率图法[11]、MaxUr法[12]、零效应搜索法[13]等,作为拒活错误小的分析方法[14]。此处笔者选取零效应搜索法进行因子筛选。
3.2 因子筛选
其基本步骤如下:
(1)首先由各因子水平xij及观测值y1,y2,…yn,得到各因子的次序统计量SSj为:
(2)
将SSj从小到大排列得到次序统计量,设m个因子中零因子的个数为s,3≤s≤m,记作:
ξr=SSr,m,r=1,2…s
(3)
(2)当3≤s≤m时,依次计算:
(4)
(5)
(6)
由式(4~6)可得到检验统计量Ws为:
(7)
(3)按照SSj由大到小的顺序比较Ws~Ws,α的值,找出满足Ws>Ws,α的最小smin,则零效应因子的个数为λ=smin-1,显著因子个数为m-λ。
为此,首先根据L12(211)正交饱和试验设计,对11个参数进行12次仿真试验后进行数据处理,根据上述步骤,得到零效应搜索法的相关参数值,如表4所示。
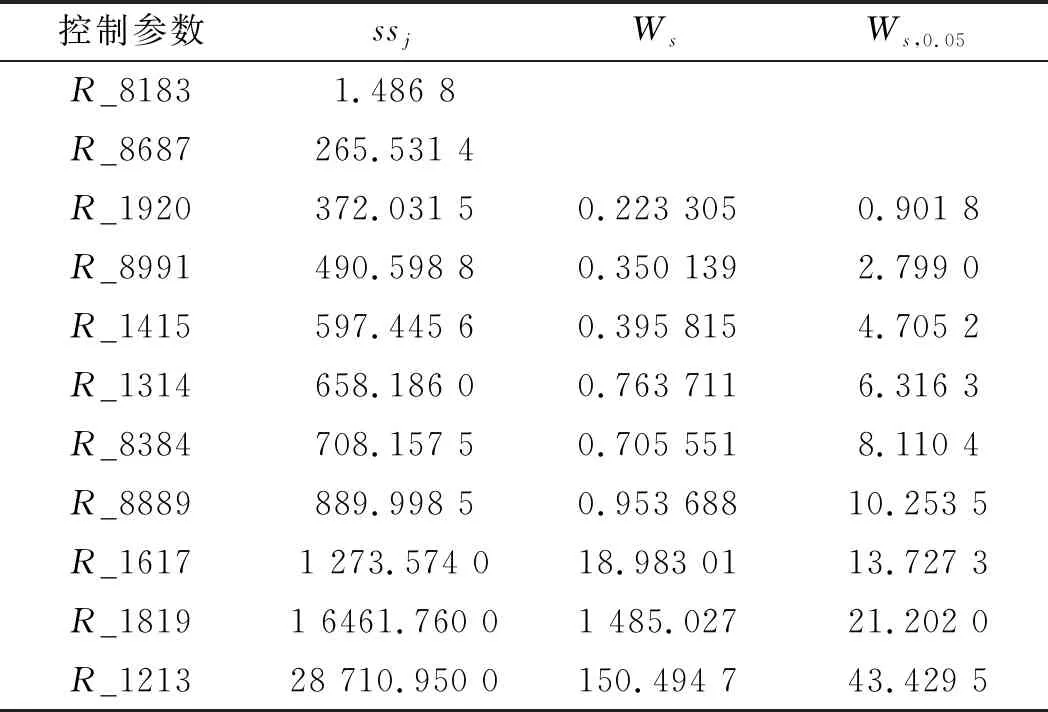
表4 零效应搜索法相关参数值
由表4可知:显著因子为R_1617,R_1819,R_1213,故笔者选取以上述3个因子作为设计变量,以降低应力值。
4 区间不确定性稳健设计
4.1 设计变量的选取
在工作过程中,转向节所受载荷复杂多变,且其变化的概率密度函数不能提前获得,为降低载荷变化对最大应力值得影响,寻求最佳的转向节长臂设计变量,笔者利用区间不确定性稳健设计进行优化。其优化模型为:
(8)
式中:X—设计变量;R—不确定因素;V—体积约束;V0′—拓扑优化后的体积;RI—不确定因素的上下限;RR—不确定因素的上限;RL—不确定因素的下限;Ωn—设计变量的N维空间。
在此处,不确定因素即0.4 g转向时的载荷大小,取载荷值较大的3个载荷为不确定因素,记为F1、F2、F3,以表1所示设计变量数值大小为初值,取其变化范围为±10%,则其初值大小为:F1=4 732.2,F2=8 798,F3=8 485.7。
由于不确定因素的存在,使得每组设计变量都对应一组目标函数值,为比较一个区间函数值是否优于另一个区间函数值,笔者采用区间序转换模型,常用区间的中点Rc及区间半径Rw表示每个区间,其定义为:
(9)
采用对区间中点及宽度偏好的区间序关系,比较不同区间数的优劣关系,即:
min(Rc(X),Rw(X))
(10)
此时,不确定优化问题转换为确定性优化。笔者采用两层嵌套的优化流程完成上述转换,即内层优化用于求得每组设计变量所对应的由于不确定因素导致的区间值,外层优化对设计变量进行优化。
4.2 优化设计
为了提高优化效率,笔者在Isight中建立双层嵌套优化模型,采用拉丁超立方采样得到32组数据,然后建立克里金插值模型[15]进行优化。
优化算法选择方面:对外层优化而言,由内层优化得到的优化区间往往是非连续、不可导的,且外层优化应对全局范围内的设计变量有较好的探索性能,故笔者选择NSGA-Ⅱ优化算法;对内层优化而言,考虑其全局求解能力及计算效率的要求,多岛遗传算法能满足上述要求。
在Isight中迭代240次,在众多可行解中选取迭代次数为180次时为最优解,最终得到设计变量的值为R_1213=114.1 mm,R_1617=47.4mm,R_1819=55.3 mm。
4.3 优化结果验证
将上述结果进行有限元分析后,可得到优化前后对比结果如表5所示。

表5 形状优化前后对比结果
由表5可知,通过拓扑优化可实现减重6.9%,通过形状优化进一步减重,总减重比达7%;另一方面,虽然拓扑优化使得0.4 g转向工况下的最大应力值上升,但通过形状优化,使得0.4 g转向下的最大应力值减小为171 MPa。
为验证优化结果的准确性,笔者对优化后的转向节进行工程化处理,增加倒角、拔模斜度、小孔、凸台等特征,将优化后铝合金转向节进行试制,所用工艺为精密热锻造,得到的转向节实物如图6所示。

图6 优化后转向节实物图
笔者将转向节样品交由某机构进行疲劳耐久性检验,要求试验后转向节、转向节臂均不得出现断裂等损坏现象。
试验结果如表6所示。
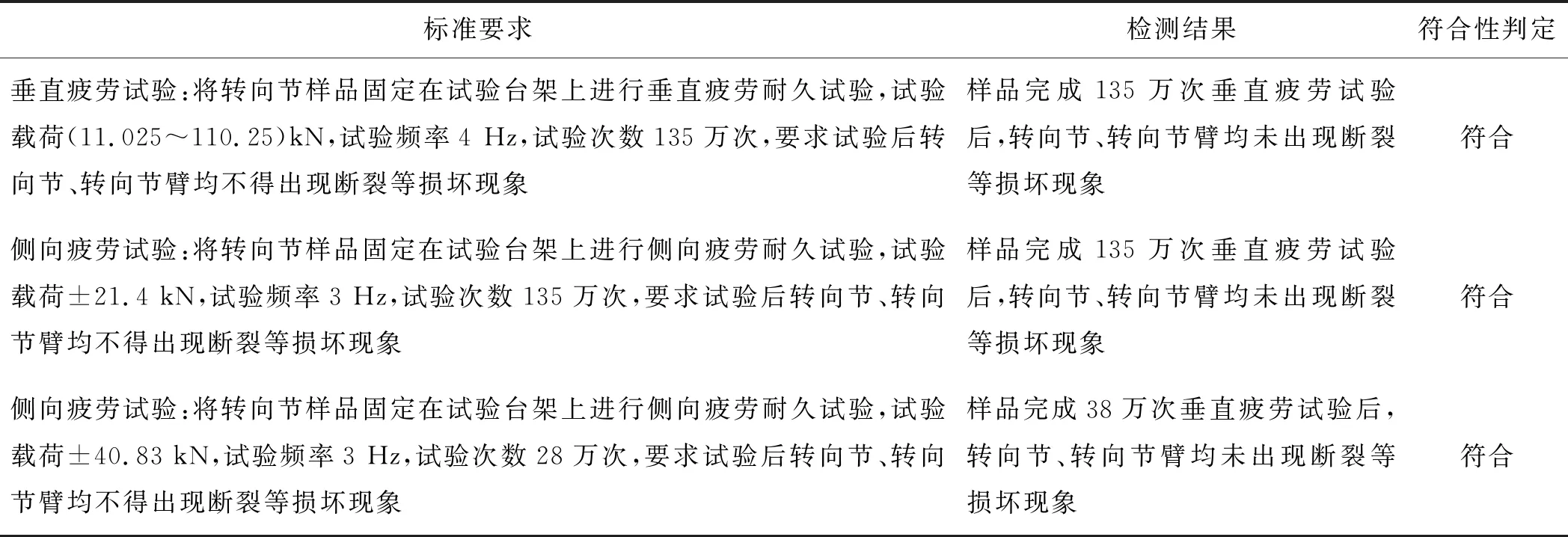
表6 疲劳耐久性试验结果
由表6可知,结构优化后的转向节符合以上性能要求。
5 结束语
针对转向节轻量化设计难度大的问题,笔者以加权柔度为优化目标,同时考虑转向节3种典型工况,得到了较为清晰的材料分布路径;参考拓扑优化的结果,并通过对应力集中区域进行了稳健性形状优化设计,结果表明:
(1)最终得到的铝合金转向节减重达7%,同时降低了转向工况的最大应力值;与拓扑优化结果相比,应力值由185 MPa降为171 MPa;
(2)通过无重复正交饱和试验的方法以减少试验次数,同时通过零效应搜索法实现显著性检验,从11个参数中得到3个显著因子作为设计变量以减少优化工作量,提高了优化效率;
(3)考虑到转向节工作过程中载荷的不确定性,笔者对0.4 g转向工况进行区间不确定性分析,提高了优化结果的安全性与可用性。
