基于神经网络和证据融合的液压泵故障诊断研究*
2020-12-24朱冠霖王兆强王异凡李志峰孙崇智
朱冠霖,王兆强*,王异凡,李志峰,孙崇智
(1.上海工程技术大学 机械与汽车工程学院, 上海 201620;2.国网浙江省电力有限公司 电力科学研究院,浙江 杭州 310007;3.甘肃省特种设备安全技术检查中心,甘肃 兰州 730020;4.甘肃省特种设备检验检测研究院,甘肃 兰州 730050)
0 引 言
随着机械工业的发展,对机械设备故障诊断的要求也进一步提高[1,2]。柱塞泵一类的液压泵是各类机械动力的输出端,由于其位置的重要性,已经有很多专家学者都对其展开了故障诊断方面的研究[3,4],比如基于经验小波分解和卷积神经网络的液压泵故障诊断等。
一般来说,液压泵(柱塞泵)一旦发生故障,故障会反映在某些特征信号上,使用信号增强技术可对故障特征进行提取[5]。故障检测可通过与已知的理论故障特征进行匹配来实现,但不同的故障类型往往具有相似的特征频率。此外,液压泵有些故障机制尚不清楚,很难给出相应的理论特征作为故障模式的标准[6]。
神经网络算法可以有效解决这类问题,在液压故障诊断等领域得到广泛应用。文献[7]使用PNN概率神经网络,实验选取5阶固有频率作为特征值输入到诊断网络中,结果发现可以较好地识别出复杂环境下的液压系统漏油故障。文献[8]使用经验模态分解与神经网络相结合的方法对柱塞泵进行故障诊断,实验发现该方法可以大幅减少诊断时间。本文将基于神经网络算法对液压泵进行故障诊断。
另外,目前关于液压泵的故障诊断大多依赖于单一传感器来诊断,但是现实环境中由于高温、强电磁等复杂环境的影响,传感器并不总是可靠的[9]。因此,可基于D-S证据理论对多源信息进行融合,从而提高诊断效果[10]。
针对证据组合存在的问题[11,12],笔者对原始证据进行修正,并通过类比引力定律定义两证据间的引力,进而提出新的衡量证据冲突程度的系数,最后通过案例验证该方法的有效性,为柱塞泵一类液压泵的故障诊断提供技术借鉴。
1 粒子群神经网络分类理论
目前,基于前馈型(BP)神经网络[13]的故障识别技术在液压故障诊断领域得到了广泛的应用。可通过将粒子群(PSO)融入BP神经网络中[14],以此提高BP网络的全局寻优能力。
设由m个粒子在D维目标搜索空间中组成一个群体,其粒子更新公式为:
xid(t+1)=xid(t)+vid(t+1)
(1)
vid(t+1)=vid(t)+c1r1(pid-xid(t))+c2r2(pgd-xid(t))
(2)
式中:i—粒子序号;d—粒子维度;t—迭代次数;c1—认知因子;c2—社会因子;r1、r2—[0,1]上的随机数;xid(t)—第i个粒子迭代t次后的位置;vid—第i个粒子迭代t次后的速度;pid—第i个粒子当前的最优位置;pgd—粒子群当前的最优位置。
对于c1和c2,加入动态调整参数如下所示:
(3)
(4)
式中:α、β、γ、δ—设定参数值;maxgen、i—粒子群设定的最大进化代数、当前进化代数。
PSO-BP中粒子的适应度函数如下所示:
(5)
式中:P—样本总数;s—输出层个数;yk—实际输出值;tk—期望值。
2 证据理论
2.1 D-S证据理论
在对液压泵中多个传感器信息融合时,由于人为或环境方面的原因导致测量值不准确甚至是出现缺失的情况,而D-S证据理论就可以处理这些信息融合中存在的不确定性。
D-S基本概率分配函数如下所示:
(6)
式中:Ai—概率分配函数焦元;Θ—辨识框架,满足2Θ→[0,1](2Θ是Θ中所有子集组成的集合)。
利用D-S证据理论进行组合的规则公式如下所示:
(7)
式中:m1、m2—概率分配函数;Bj—概率分配函数的焦元;k—冲突系数。
其中:
(8)
2.2 证据融合改进
证据理论对信息进行合成时,往往会出现与事实相悖甚至是融合算法失效的问题[15]。本文在传统的数据融合基础上进行相应的改进,以两条证据融合为例,具体步骤如下:
(1)修正原始故障证据分配值,如下所示:
(9)
式中:n—焦元A对应的事件个数。
然后对各个数据进行权重计算,方法如下所示:
(10)
(2)计算证据体间的距离,如下所示:
(11)
(3)计算两条证据间的熵值H1、H2,如下所示:
(12)
(13)
式中:pi—m1函数对应的各概率分配值;qi—m2函数对应的各概率分配值。
(4)计算两条证据间的引力F,如下所示:
(14)
(5)计算两条故障证据间新的冲突系数F*,即将式(14)中计算得到的作用力映射到区间[0,1]上,计算方法如下式所示:
(15)
(6)对证据体进行融合,公式如下:
(16)
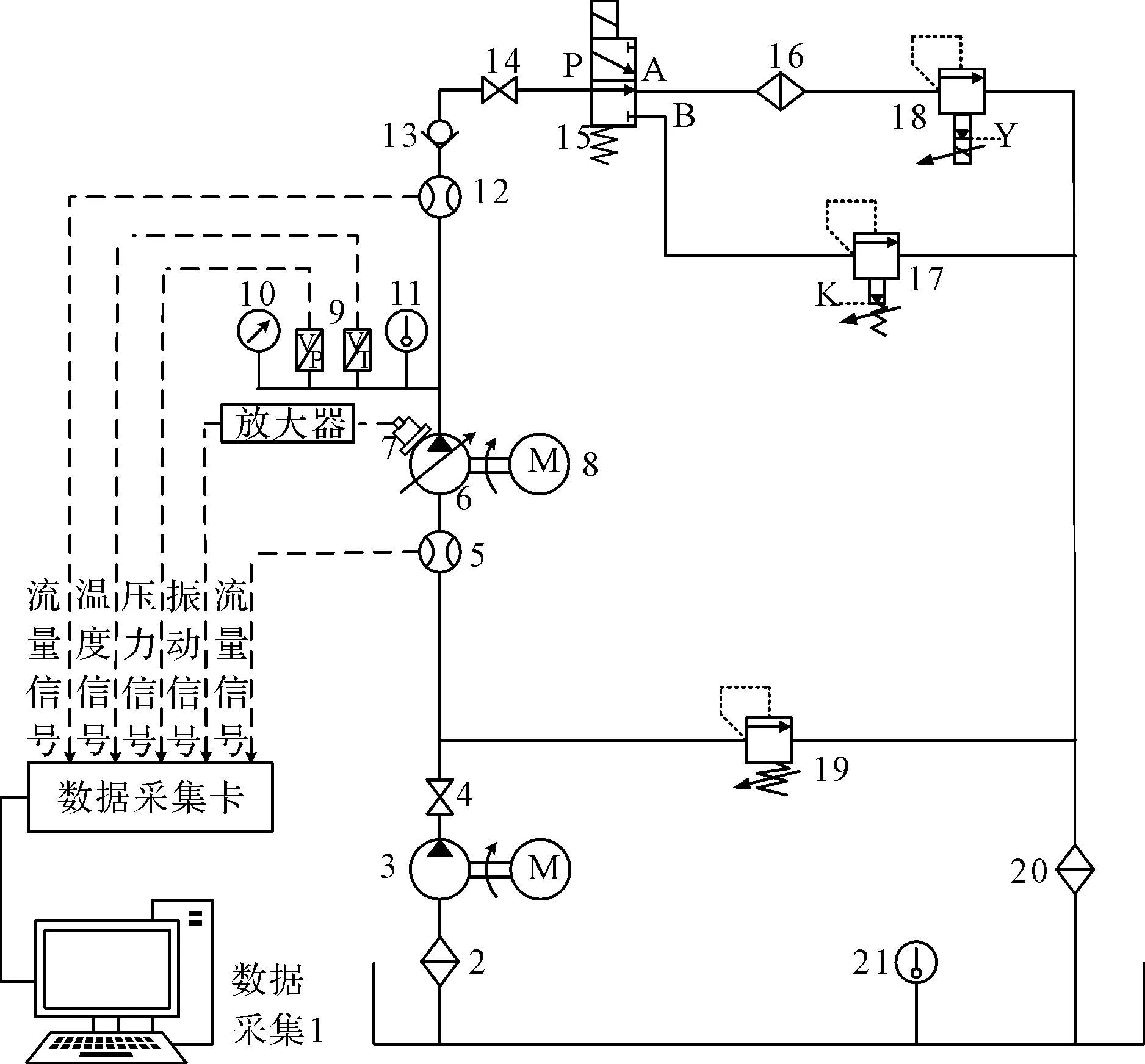
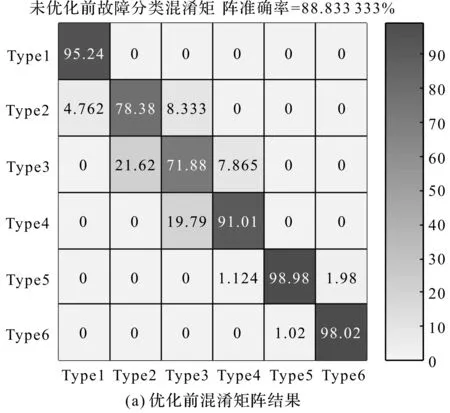
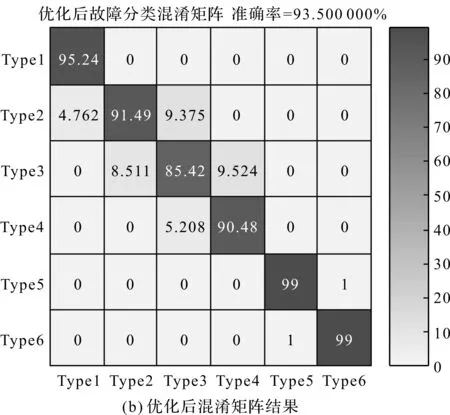
(7)对冲突系数设置阈值T,当F*>T时,直接输出第6步中的融合结果。若F* (8)对初始融合的故障结果设置阈值,当m(A)<λ时,对结果乘以一个衰减系数α,以进一步减小故障支持度较低的权重大小,然后计算各个数据权重,得到最后结果。 笔者设计故障诊断模型,选择出油口的振动信号、外泄口温度以及系统出油口的压力信号作为传感器测试源,以此作为模型的入口。 具体故障诊断融合模型如图1所示。 图1 故障诊断融合模型 笔者将采集的振动和压力信号分别计算出8个特征指标(峰值、波形指标、脉冲、裕度指标、峭度指标、频域方差、功率谱重心指标、相关因子)来构造特征空间,并和温度数据进行归一化处理,分别构造正常及故障状态下的数据训练库。使用三级PSO-BP分类算法、改进的D-S证据理论进行融合诊断。 为了验证故障诊断模型及对应算法的有效性,笔者设计柱塞泵模型诊断实验,通过放置已知故障类型的柱塞泵,或者更换内部故障的滑靴、配流盘等构造故障模型,进行模拟实验。 一般情况下,带有故障的柱塞泵自吸性能差,所以在测试系统油路中加入两个叶片泵进行补油。 实验原理图如图2所示。 分别构造正常状态、失效油封漏油故障、缸体切割深度0.5 mm,宽度0.3 mm、轴承切割深度0.5 mm,宽度0.2 mm、配流盘磨损0.3 mm、活塞间隙0.25 mm的松靴故障这6种状态进行检测,即模式输出Y={f1、f2、f3、f4、f5、f6},每种模式对应的故障输出训练矩阵如表1所示。 图2 实验原理图1-油箱;2,16,20-粗过滤器;3-叶片泵;4,14-截止阀;5,12-流量计;6-被测轴向柱塞泵;7-振动传感器;8-变频电机;9-信号调理模块;10-压力计;11-温度传感器;13-单向阀;15-二位三通电磁换向阀;17-先导式溢流阀;18-先导式比例溢流阀;19-直动式溢流阀;21-油液温度计 表1 故障输出训练矩阵 笔者对每个子网测试提取的指标数据各选取500条作为网络训练集,500条作为故障诊断测试集进行故障类型分析。构造3层子神经网络,输入层对应特征指标的个数为8,输出层对应故障类型数量为6,根据实验经验,这里设置隐含层数为15,粒子群规模20,迭代次数1 000次。两个学习因子中的参数分别取0.5、1、2、1。 由实验得出振动分类混淆矩阵结果如图3所示。 图3 振动分类混淆矩阵结果 对于振动子网诊断结果可知,优化前的故障分类准确率为88.83%,优化后的故障分类准确率为93.5%。其中优化后的混淆矩阵显示:模式2的4.762%被识别为模式1;模式3的8.511%被识别为模式2;模式4的5.208%被识别为模式3;模式5的1%被识别为模式6,错误率较未分类均有所改善。 对于压力子网分类混淆矩阵结果如图4所示。 图4 压力分类混淆矩阵结果 对于压力子网,优化前的故障分类准确率为89.83%,优化后的故障分类准确率为93.67%。其中,优化前的混淆矩阵显示,模式3的12.5%被识别为模式2,模式4的16.94%被识别为模式3,错误率较高,这两者经过优化后结果分别为8.247%和9.184%。同样,对于温度子网来说,优化后的效果要优于优化前的诊断效果,这里不再详细分析。 以f5类故障为例,设置证据融合阈值λ为0.5,衰减系数α取0.2,利用3个独立子网及改进的D-S算法诊断输出结果如表2所示。 表2 各诊断输出结果 由表2可知:三级子网对f5类故障诊断输出结果分别是76.5%、62.5%、78.5%。经过融合算法联合诊断结果输出为99.12%。 各输出结果对比如图5所示。 图5 各输出结果对比 由图5可知:改进的融合算法对f5类轴承磨损故障支持度接近100%,对比其他子网,基本排除了其他故障类型的可能性。 同理,设置证据融合阈值值为0.5,衰减系数取0.2,将f3类故障类型分别使用子网及改进的D-S算法诊断,各诊断输出结果如表3所示。 由表3可知:各诊断子网对f3类缸体磨损故障诊断输出结果分别是78.4%、70.4%、70.5%,经过改进D-S数据融合处理后的诊断输出提高到99.17%。 表3 各诊断输出结果 各输出结果对比如图6所示。 图6 各输出结果对比 由图6可以发现,相比各子网结果,使用改进的融合算法对f3类缸体磨损故障支持度进一步提高,降低了结果的模糊性。 通过以上实验可知:采用自适应调节认知因子、社会因子优化网络分类法,对轴承磨损以及缸体磨损准确度均有一定的提升,但其正确率依赖于相关参数的选取,还需要作进一步的优化,以增强模型的稳定性。 液压泵(柱塞泵)一旦发生故障,故障会反映在某些特征信号上,使用信号增强技术可对故障特征进行提取,但液压元件在工作环境中易受到各类噪声的污染,而且存在传感器自身发生故障的情况。 笔者采用加入调节参数优化的PSO-BP局部诊断网络,发现构建的振动子网诊断正确率由88.83%提高到93.50%,压力子网诊断准确率由89.83%提高到93.67%,进一步使用所提出的改进证据理论步骤进行融合诊断,发现各故障类型诊断支持度均接近于1,有效避免了子网识别的模糊性。由此可见,其对柱塞泵的故障诊断具有一定的工程实用价值。 另外还需要指出的是,本文参数的选取具有一定的经验性,因此,将来还要进一步研究自适应试验工况最优参数选取的问题,这是今后研究的一个方向。3 故障诊断模型搭建
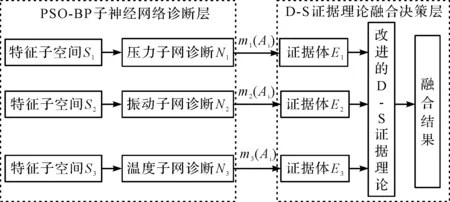
4 液压故障诊断案例
4.1 实验描述

4.2 结果分析

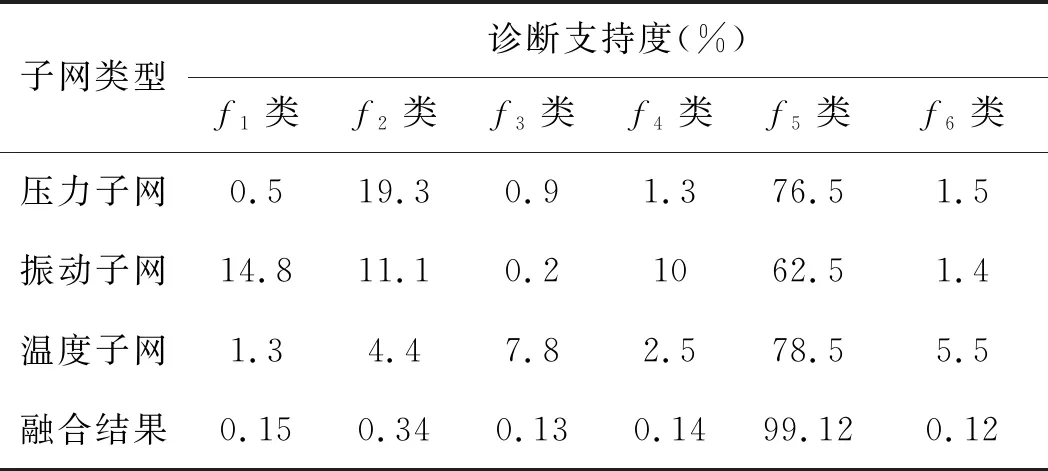
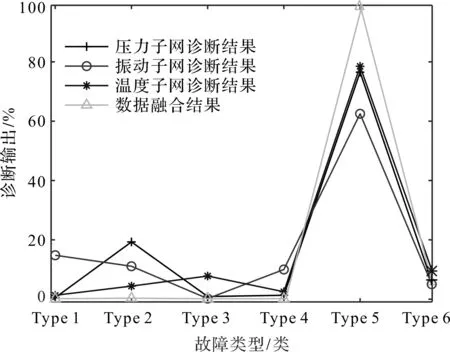
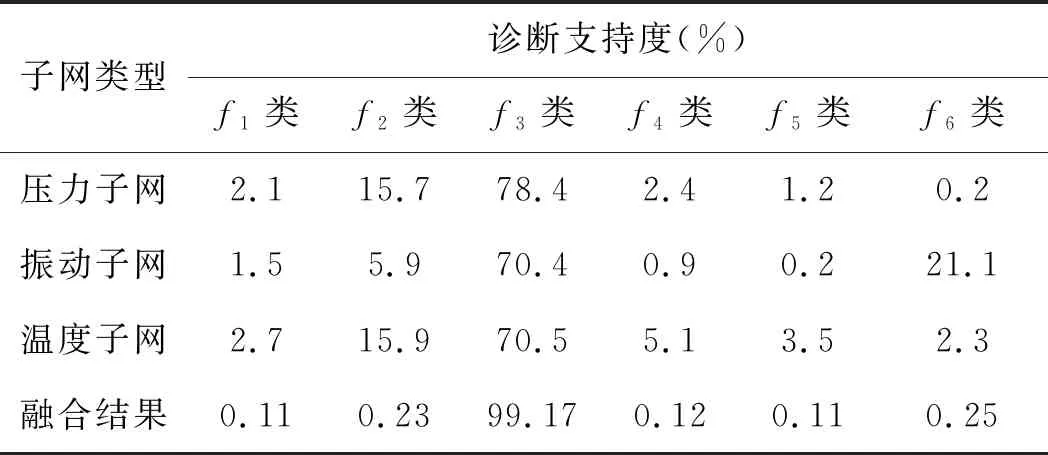

5 结束语
