分段线性复合式振动俘能器的建模与实验*
2020-12-24王浩宇彭利平刘德洋
王浩宇,杨 欢,彭利平,刘德洋
(河海大学 机电工程学院,江苏 常州 213000)
0 引 言
微机电系统和电子技术的快速发展使得微电子设备的能量消耗逐渐变小,但为其供能的传统电池存在寿命短及更换过程复杂的缺点,这促使人们探究新的无源供能方法。振动俘能器已被公认为是解决低功耗设备供电问题最具有发展潜力的技术途径。振动俘能器中最常见的能量转换机制有静电换能[1]、压电换能[2]和电磁换能[3-5]。其中,不需要额外辅助供电的电磁式能量俘能器(EEH)和压电式能量俘能器(PEH)受到了国内外研究者的更多关注。
现实中主要环境振动源在一个比较宽的低频范围内(100 Hz以下),然而大多数的振动俘能器简化为线性弹簧质量阻尼系统,振动的能量俘能器都将单峰振幅限制在窄频带内;外部激励存在与俘能器的谐振频率不匹配产生共振发散的情况[6],这使得线性能量收集器应用受到局限。另外,单一能量转换模式的能量输出往往达不到供能需求。因此,研究多种俘能技术和非线性的耦合输出具有很大意义。复合压电-电磁振动能量俘能器(HPEH)能将两种及以上的能量转换机制进行耦合,能增加耦合来提高输出能量。CHALLA[7]通过实验得出了复合振动俘能器相比任何独立的振动俘能器有更好的能量输出的结论;MAHMOUDI等人[8]开发了一种包含非线性HPEH的多物理模型,非线性磁场的系统比线性系统工作带宽和功率密度分别增加了29%和60%;SOLIMAN等人[9]提出了一种基于分段线性振子的振动俘能器,利用制动器引起梁的碰撞,频率带宽明显拓宽;MIAH等人[10]设计了基于冲击梁的向上变频压电振动俘能器,该振动俘能器与分段线性系统耦合,能够在较宽的工作带宽内产生较高的输出功率。
针对以上问题,本研究利用多个压电悬臂梁和非线性弹簧提升系统的耦合以及带宽;笔者利用欧拉-伯努利梁理论对装置进行分布参数建模;利用Rayleigh-Ritz模态分析法确定力电耦合模型的等效刚度、质量等参数,建立基于集总参数模型的机电耦合模型。该方法考虑梁的振型与轴向应变分布情况,能提高预测精度。通过加工实验装置及搭建实验平台得到实验输出值与理论值对比,验证非线性振动俘能器机电耦合模型的准确性和装置拓宽频带能力。
1 能量收集系统结构及工作原理
振动俘能器有4个压电悬臂梁,梁的自由端均与线圈连接,线圈下方设有固定磁铁和弹簧。
分段线性复合振动俘能器和HPEH的单自由度等效动力学模型如图1所示。
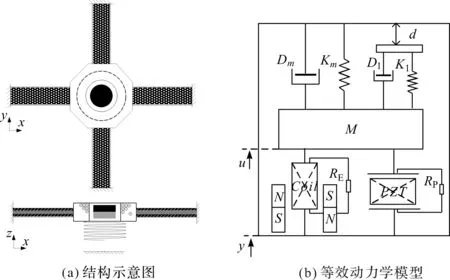
图1 分段线性复合振动俘能器
梁和末端重物会随着激励振动,压电梁产生的简谐横向振动使得压电片厚度方向发生物理变形引起了电荷运动,从而在压电陶瓷片的上下极板集聚了极性相反、等量的电荷。同样,中间的线圈随着梁上下振动,线圈切割磁感线引起磁通量的变化,发生法拉第电磁感应现象使得线圈产生感生电流。当线圈的振幅足够大时,每个周期底部弹簧都与基座碰撞,系统从线性振动转变为非线性振动的一种分段线性状态,拓宽了系统的工作带宽。
2 线性动力学模型及PEH建模
本研究移除电磁耦合和非线性弹簧,将振动俘能器简化为单自由度线性压电振动俘能器。
线性复合式振动俘能器具有良好的对称性,如图2所示。
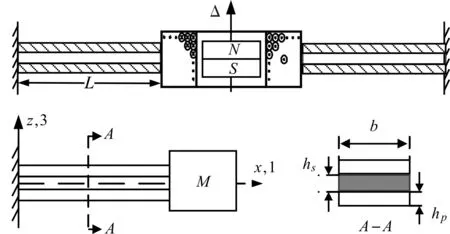
图2 线性复合式振动俘能器示意图
系统动力学特性的研究对象简化为对称的一部分,即带末端质量的固定-导支梁。在只考虑一阶固有频率的情况下,利用欧拉-伯努利梁理论和牛顿力学原理研究末端带质量的压电梁的弯曲振动位移响应,得到压电梁沿z轴无阻尼自由运动方程为:
(1)
式中:EI—压电梁平均抗弯刚度;ρs—压电梁的单位长度质量。
利用模态叠加法求解运动方程,梁上各点相对位移可以表示为:
(2)
式中:i—振型数;φ(x)—模态特征函数;q(t)—模态坐标。
运用分离变量法求解上式,将式(2)代入式(1),利用导支和固支的边界条得到频率方程为:
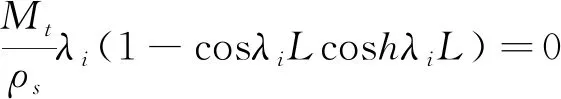
(3)
根据瑞利里兹法,导支端的位移为w(L,t)=φ(L)q(t),将系统参数等效到x=L处的位置,得到系统的等效质量M和等效机械刚度Km为:
(4)
式中:p,s—压电和基底层;S—梁的横截面积;ρ—密度;E—弹性模量;I—惯性矩;Mt—末端质量。
笔者在模态分析和压电本构方程的基础上,利用哈密尔顿原理开展线性PEH系统的机电耦合建模[11,12]。根据Rayleigh-Ritz方法,梁的横向位移可以为N个振动模态函数与模态坐标的乘积,电势函数为N个电势分布函函数和电学坐标的乘积:
(5)
式中:ψ(z,t)—电势函数;φn(x)—振动模态函数;φv(z)—电势分布函数;v(t)—电学坐标。
机电耦合等效方程简化为:
(6)
式中:θp—等效压电耦合系数;Cp—压电等效电容:
(7)
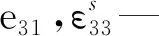
3 电磁耦合系数
电磁发电转换机制基于法拉第电磁感应定律,电磁感应结构如图3所示。
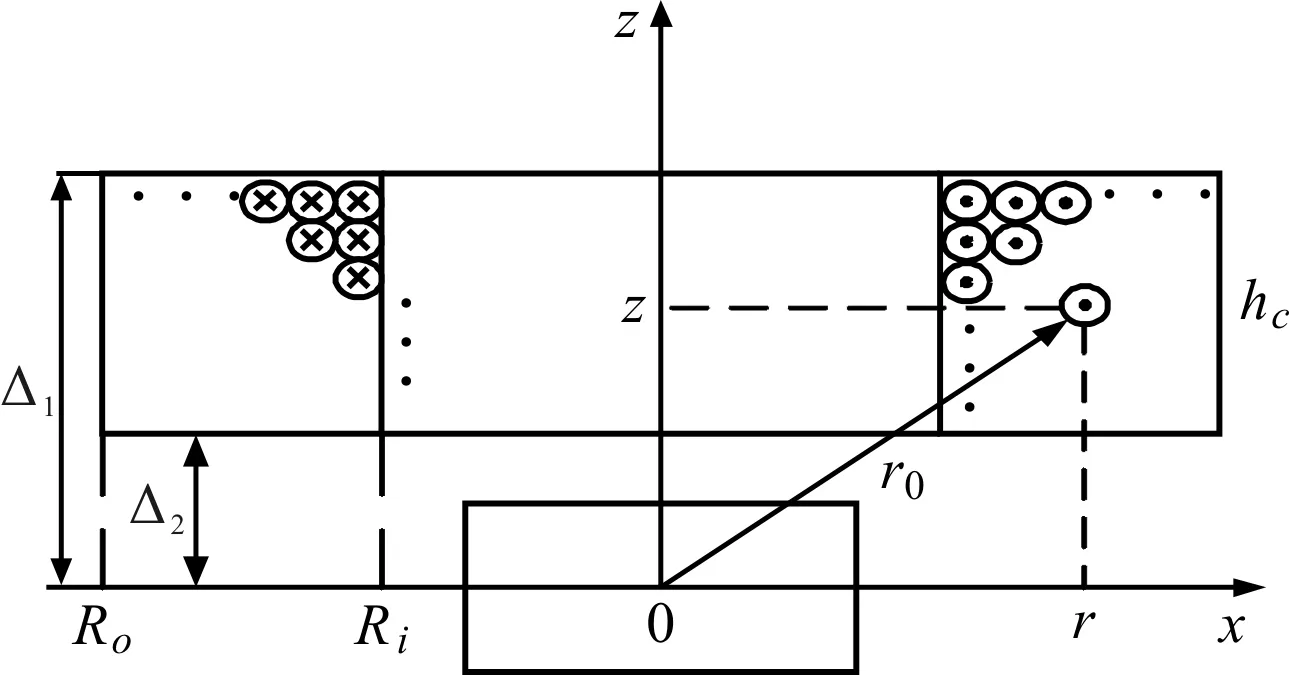
图3 电磁感应原理示意图
无论是面积恒定下变化的磁场引起的磁通量变化,还是恒定磁场下的面积变化引起的磁通量变化,均可以推导出电动势方程。工作过程中线圈振子磁场时刻变化,线圈的面积认为常数。
电动势Ue与通过线圈磁通量的变化率有关[13],表示如下:
(8)
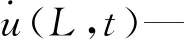
根据磁偶极子模型[14],磁偶极子模型产生的磁场在坐标(r,z)的磁场强度B为:
(9)
式中:Br,Vm—永磁铁剩磁强度和体积;ez—z方向的单位向量。
只有沿着z方向的磁场分量对感应电动势有影响,整个感应线圈内的磁通量为:
(10)
式中:fc—线圈填充率,N—线圈匝数。
将式(9,10)代入式(8)得到电磁耦合系数:

(11)
式中:Δ1,Δ2—静平衡时磁铁中心到线圈上面和下面的垂直距离。
为了便于分析和计算,一般取静平衡位置时的电磁耦合系数。
4 集总参数机电耦合模型
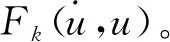
(12)
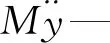
压电梁通常在低频有较好的表现,等效质量和等效机械刚度取一阶振动模态可得:
(13)
(14)
式中:K1,D1—非线性弹簧的等效刚度和阻尼。
考虑到压电和电磁机电耦合作用对系统的影响,系统的线性等效刚度为:
(15)
压电负载Rp和电磁负载Re下系统的输出功率分别为:
(16)
(17)
5 数值仿真与实验分析
为了验证理论模型的合理性,本研究在MATLAB中对机电耦合模型进行数值仿真和实验。
HPEH结构的仿真相关参数如表1所示。
实验模型样机及验证实验平台如图4所示。
实验系统主要包括:信号发生器为DH5922N、功率放大器为DH5872、激振器为DH40200、位移传感器为HG-C1050、加速度传感器1A941E、数字示波器、外接电阻负载。功率放大器根据信号发生器输出的频率可调正弦激励信号控制激振器振动,从而为俘能器提供恒定的激励源,同时采用加速度传感器和位移传感器对振动加速度以及输出位移进行测量。
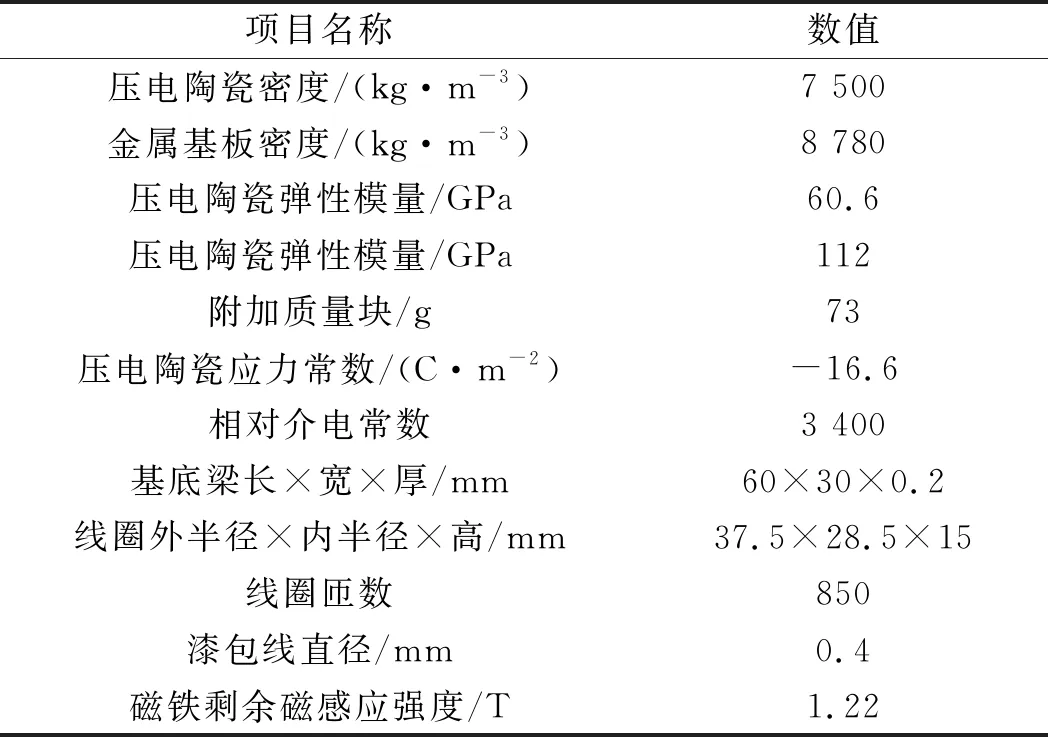
表1 HPEH结构参数相关参数

图4 模型样机及验证实验平台
本研究利用MATLAB对无弹簧复合俘能器系统进行扫频,测试发电能力。在0.2 g加速度激励下研究系统的电压变化情况。
振动俘能器的扫频仿真和实验如图5所示。
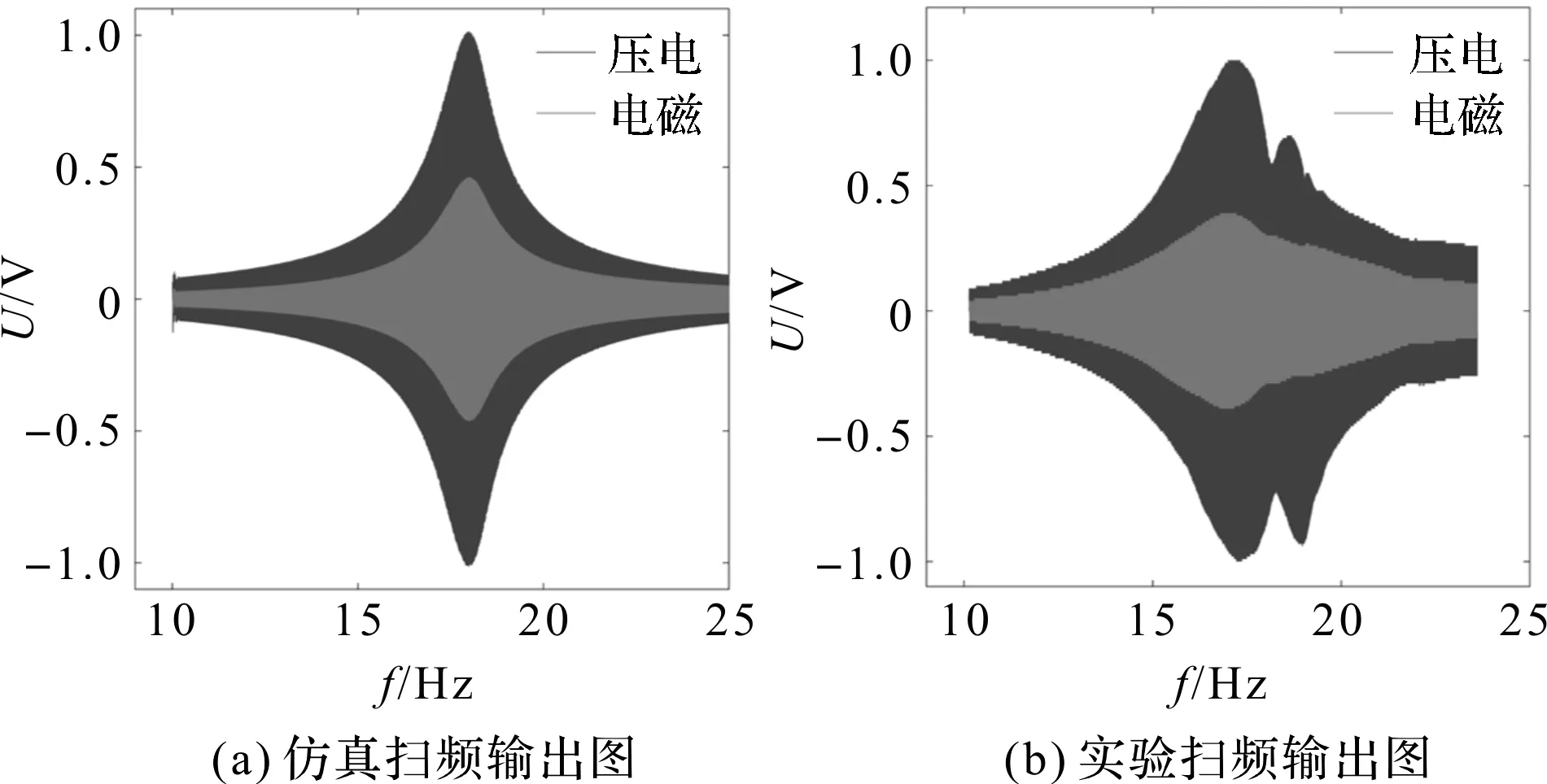
图5 线性HPEH扫频最优负载电压输出图
系统仿真固有频率为17.5 Hz,实验得到一阶固有频率为17.2 Hz,理论与实验较为接近。
为了得到系统的最优负载,分别对PEH和EEH进行功率优化。在17 Hz、0.2 g加速度下分别对PEH和EEH接入不同的负载,获得电压和功率随负载变化情况。
PEH、EEH电压、功率随电阻变化如图6所示。
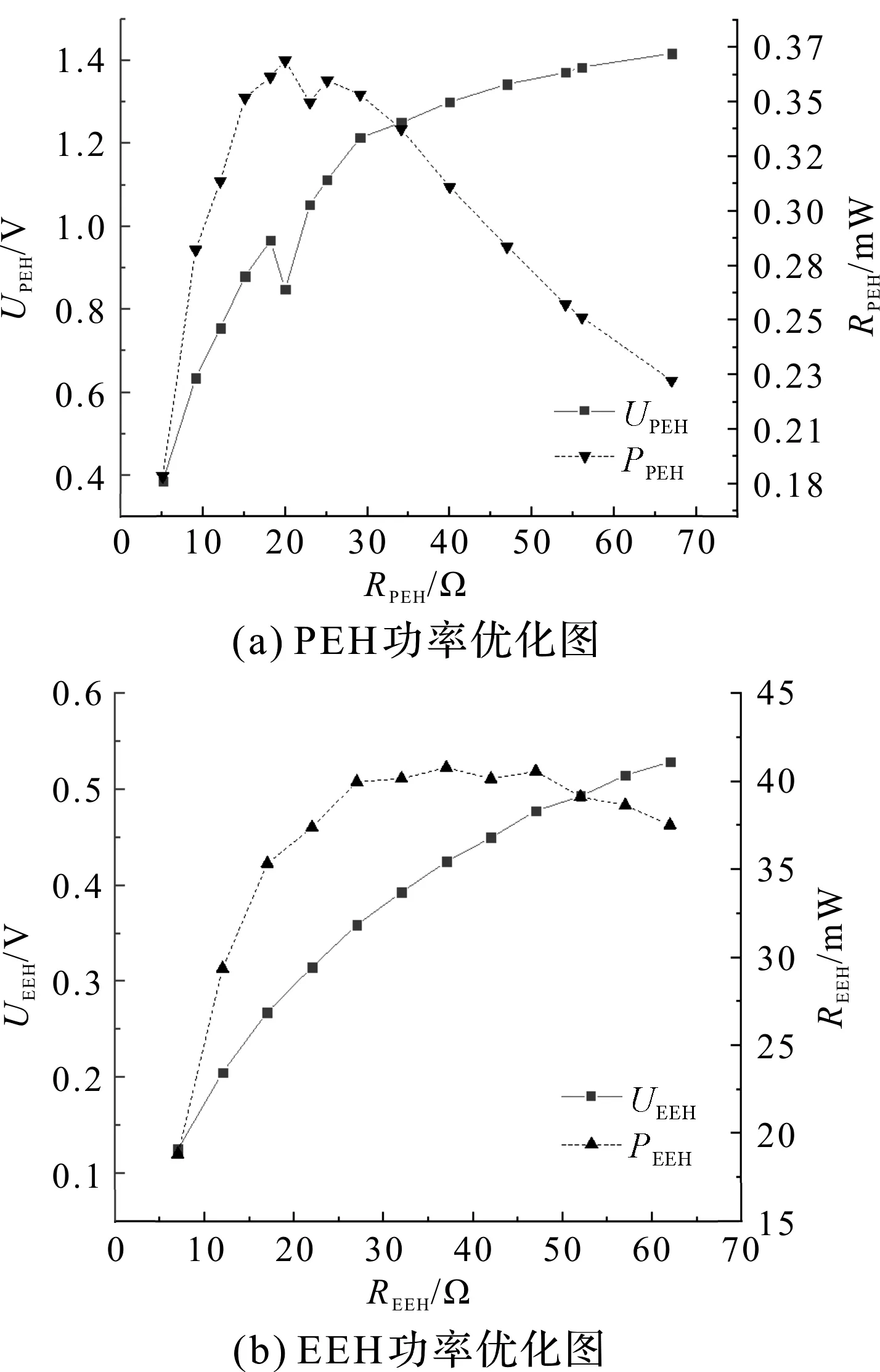
图6 PEH、EEH电压、功率随电阻变化曲线
其电压随着阻值的增加而单调增大,输出功率则先上升到某个值后逐渐下降。实验得到PEH和EEH的最佳负载分别为18.2 kΩ和37 Ω。
单一俘能器最优负载的电压、功率随频率变化如图7所示。
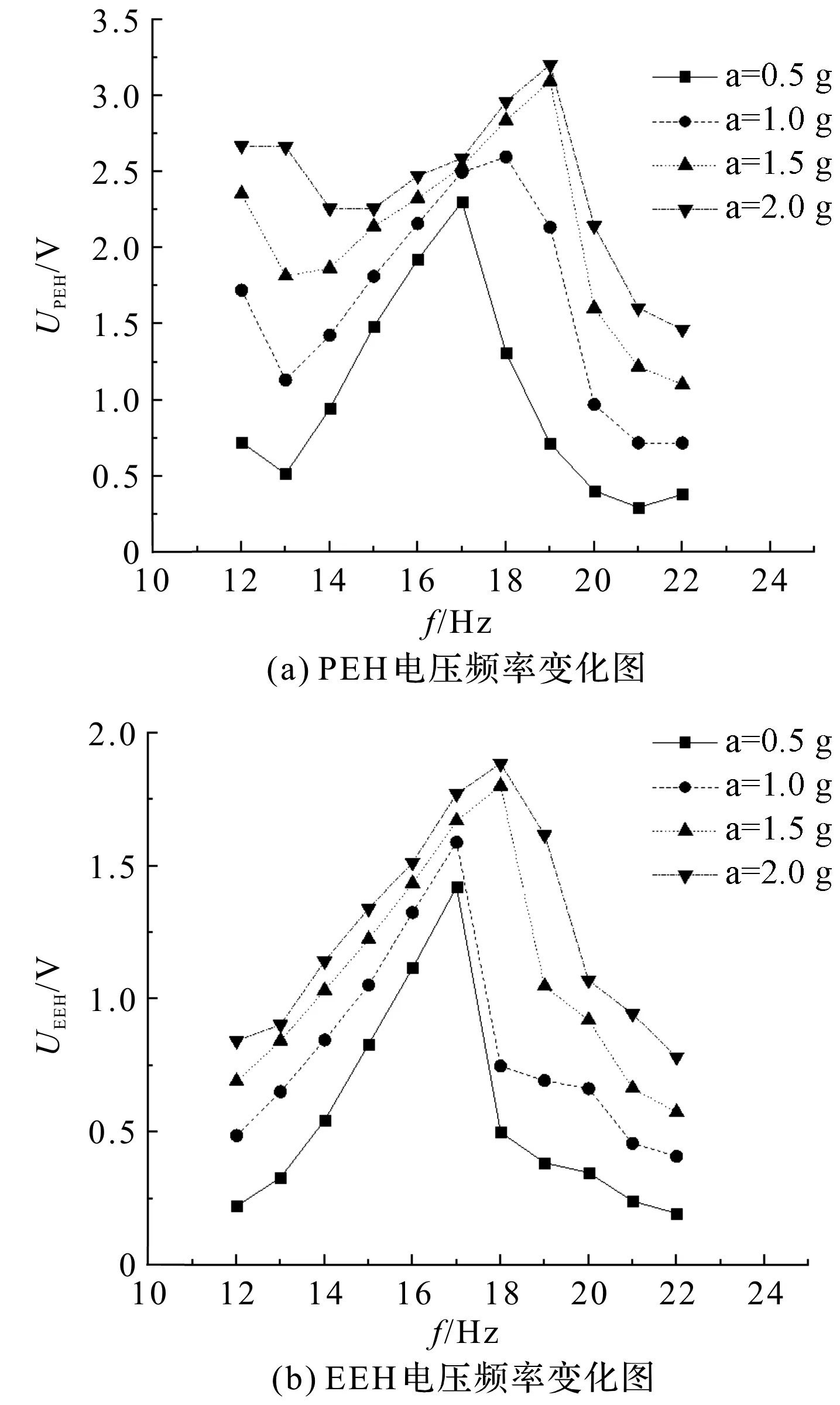
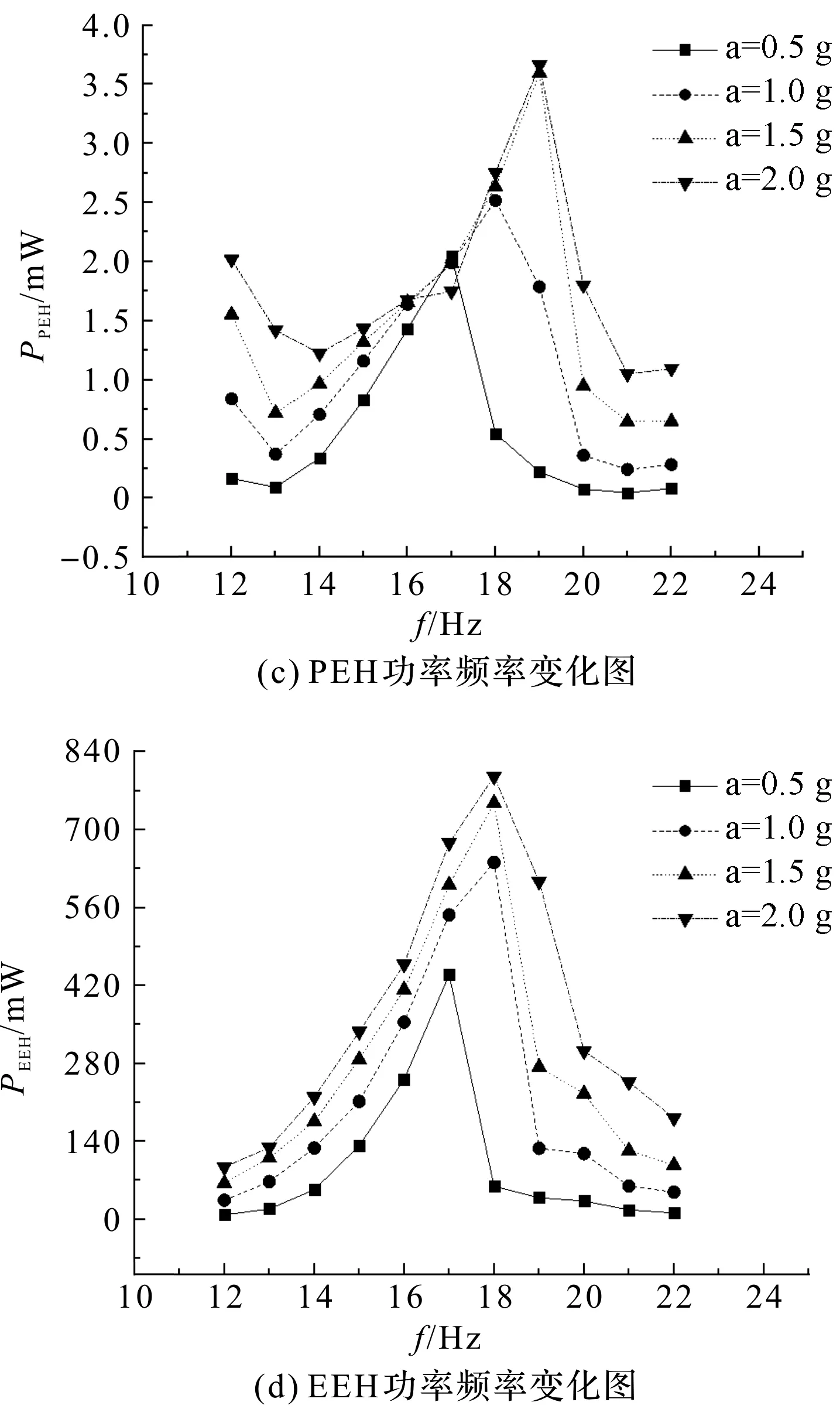
图7 单一俘能器最优负载的电压、功率随频率变化图
PEH、EEH的电压输出和功率输出随着激励的增加而增加,同时他们的峰值随着激励的增大向右产生偏移。产生这种现象的原因是结构具有非线性,较高激励使得梁的刚度增加影响了固有频率。
线性HPEH功率随频率变化如图8(a)所示。对比理论分析结果和实验结果发现,线性HPEH的理论模型与实验结果较为吻合。线性HPEH的复合功率在17.8 Hz处达最大值,最大输出功率为682 mW。
为了探究不同激励对于系统输出的影响,线性HPEH输出随频率、加速度变化如图8(b)所示。系统功率输出的最大值随着激励的增加而偏移,产生这种峰值偏移的原因可能是耦合的增加使得系统向右偏移。
最后对非线性弹簧HPEH的发电性能进行最优负载的仿真和实验。
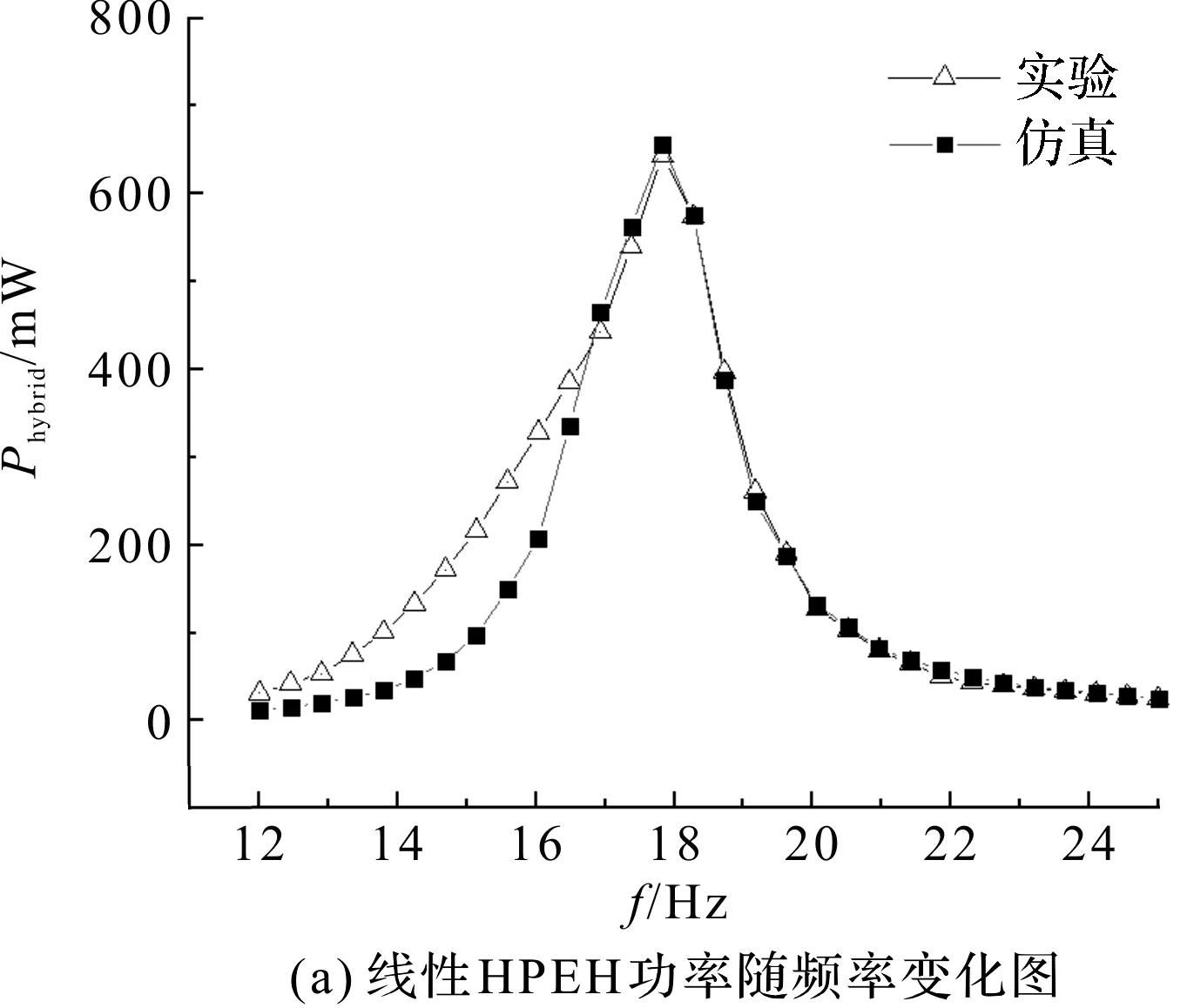
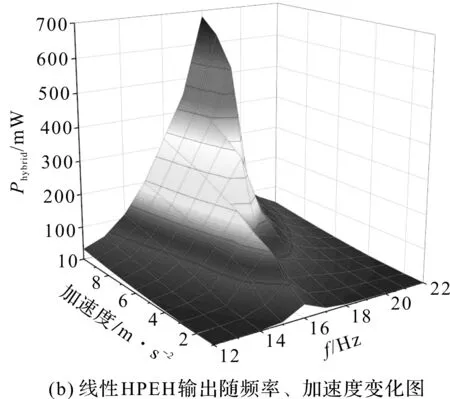
图8 线性HPEH功率随频功率变化关系图
分段线性HPEH不同刚度功率输出随频率变化如图9所示。
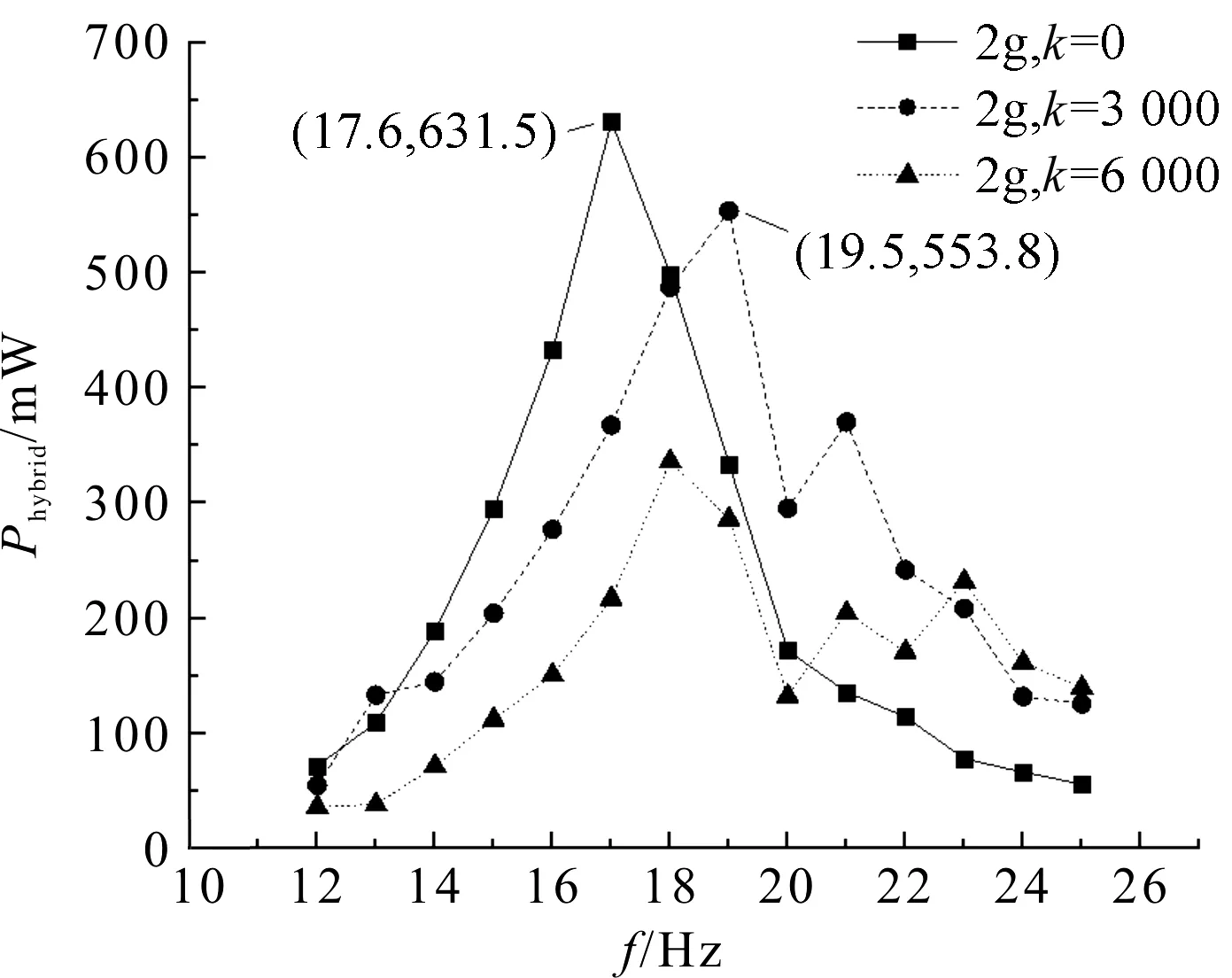
图9 分段线性HPEH不同刚度功率输出随频率变化图
对比发现分段线性HPEH具更宽的带宽。除了在原有一阶共振处有较高的输出,随着弹簧刚度的增加系统会在右侧产生的次共振峰值,且两个峰值功率随着刚度的增加而下降。产生这种现象的原因可能是大刚度的弹簧阻尼也越大,影响了系统的输出。
分段线性HPEH输出功率随加速度激励变化如图10所示。
复合功率的带宽随着系统激励的增大而变宽,并且一阶固有频率有向右偏移的趋势,刚度越大偏移越明。在k=3 000 N/m条件下,优化后的负载输出功率最大值,约为27.6 mW/g2。
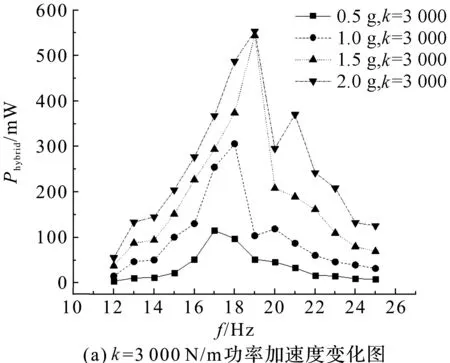
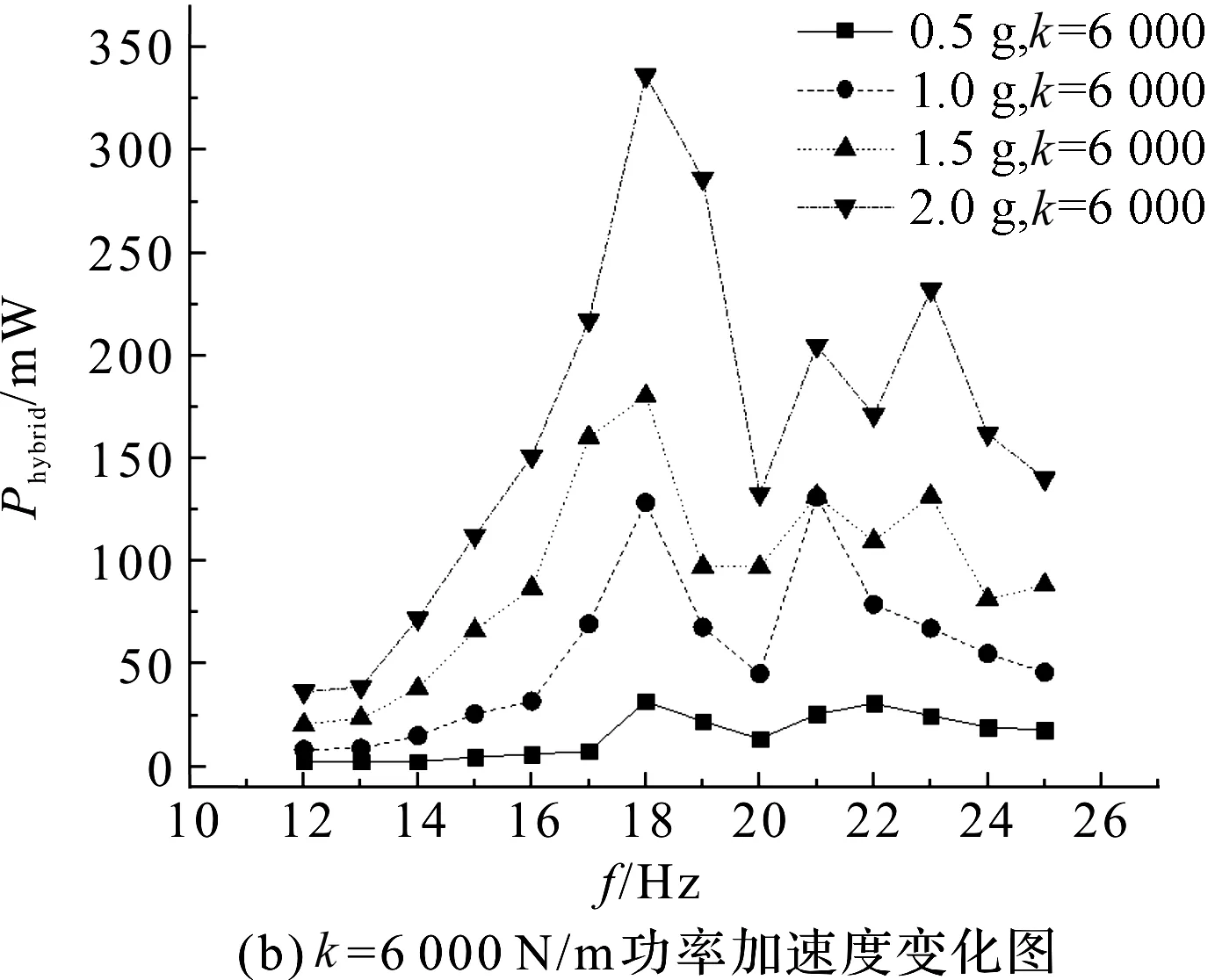
图10 分段线性HPEH输出功率随加速度激励变化图
6 结束语
本研究提出一种分段线性复合式振动俘能器,建立相关机电耦合模型并进行相关实验验证理论。分析了分段线性俘能器能够拓展带宽的原因,探究达到最大输出功率下的最优负载。
研究结果表明:分段线性的复合振动俘能器在原有共振频率的右侧会产生一个次峰值,同时该等效固支-导支梁结构本身具有非线性,这两种现象均能拓展带宽。
通过实验与数值仿真得到:系统输出电压随着负载的增大单调增加,而输出功率随着负载的电阻增加逐渐增大到某个最值后逐渐减小。在最优负载、工作频率为19 Hz时,分段HPEH最大输出功率达到27.6 mW/g2,产生的能量能够满足网络传感器等低耗能微电子产品的供能需求,在工程中具有一定的价值。
