疫情下建立股票投资组合

夏婧 山军

[摘    要] 目前我国经济运行进入一个非常复杂的阶段，受各种因素影响，经济的增速处于稳中下行状态，叠加新冠疫情的全面暴发，如何在此逆境中前行，是每个投资者乃至每个家庭都必须直接面对的问题。本文通过对疫情中各产业深度剖析，选择出四个能抵御风险，发展前景良好的行业进行股票投资，并利用层次分析法赋予权重，从而建立起一个有效应对疫情，能获取一定正收益的股票投资层次分析模型。

[关键词] 层次分析法;新冠疫情;投资组合

doi ： 10 . 3969 / j . issn . 1673 - 0194 . 2020. 21. 054

[中图分类号] F830.9   [文献标识码]  A      [文章编号]  1673 - 0194（2020）21- 0122- 02

1      问题的提出

2019年12月新冠疫情自武汉开始蔓延，短短数月扩散到全国，其传播的规模和范围前所未有，危害性远大于2003年的“非典”，得力于我国政府的强有力防控措施和对疫情的高度重视，短时间内疫情在我国国内即得以有效控制，但对经济造成的影响仍不能低估。从三个产业看，第三产业是首当其冲，其次是第二产业，最后是农林牧渔。先看第三产业，在2020年GDP的总量已超过100万亿元，其增加值占GDP的比重已达54%，分析其构成：批发零售占17.9%，金融占14.4%，房地产占13%，餐馆和住宿占3.4%。批发零售占比最大，但由于网购居多的缘故受疫情影响不大，此行业可作为股票投资选择。房地产行业2020年第一季度的销量回落明显，政府也一再强调“房住不炒”，而金融涉及外汇、股票、期货等市场，疫情会改变参与者预期从而增大波动风险，餐饮等服务消费行业则受疫情负面影响更为直接，故都不列为选择对象。

新冠疫情对第二产业的影响在我国政策对冲下会偏正面。第二产业主要包括工业和建筑业，工业中的出口商品制造业由于国外疫情愈演愈烈，可能存在订单会减少甚至取消的负面影响，但与“新基建”相关的各行各业，尤其是5G、人工智能、工业互联网、物联网等都会受益于政府大力提倡而前景看好，另外，與新能源汽车相关的行业由于政策扶持，加上契合行业发展方向，预测近几年仍会保持年复合45%左右高速增长率，所以“新基建“、新能源汽车两个行业也可列为股票投资选择对象。

疫情对第一产业的影响正面，虽然我国主粮基本维持自给无需担忧粮食安全，但粮食作为刚需，容易成为抗风险和抗通胀的主力资产，价格易涨难跌，国外疫情防控不利也会进一步推动农产品价格，所以农林牧渔行业可作为最后一个股票投资对象列入选择。

综上所述，我们确定了四个能够抵御疫情影响，并仍有良好发展前景的行业进行股票投资：批发零售、新基建、新能源汽车、农林牧渔。那么，下一步的问题是，我们如何对投入的资金在这几个行业中进行合理分配，可以让我们在获取尽量高的收益同时能规避大的风险？

层次分析法为这一类问题提供了一个比较好的解决思路：通过建立层次分析模型计算出四个行业各自的权重，然后按照权重的大小进行资金的合理分配，再运用这些资金买入各行业具有代表性的个股。由于资金的分配更加合理，可保证获取的收益和风险的承担更加优化。

2      建立层次分析模型

2.1   构建层次结构

对于股票投资，有三个基本准则可以考虑：①投资回报时间;②收益率;③投资风险。而通过之前行业剖析，提供了四个前景良好的行业供方案层选择，进而构建层次结构，见表1。

2.2   构建两两比较判断矩阵

2.2.1   构建C层对X层的比较判断矩阵A

（1）根据1-9及倒数作为标度的标度方法，给出下面比较判断矩阵：

A=  1       3    21/3     1   3/21/2   2/3   1

（2）运用matlab软件可求出比较判断矩阵A的最大特征值λmax、特征向量ω（2）：

ω（2）=0.549 90.240 20.209 9，λmax=3

（3）一致性检验。计算A的一致性指标，由于 CI（2）===0，可知A具有完全一致性，因而一致性检验得以通过。 2.2.2   构建方案层P对准则层C的比较判断矩阵Bk（k=1，2，3）

B1=  1      5     3    5/41/5     1   1/2   1/41/3     2     1    1/24/5     4     2     1，B2=  1     1/3  1/5   2/3  3      1    1/2   2/3  5      2     1       33/2   3/2   1/3     1

B3=  1      2      3    6/71/2     1      2   1/21/3   1/2     1   2/77/6     2    7/2    1

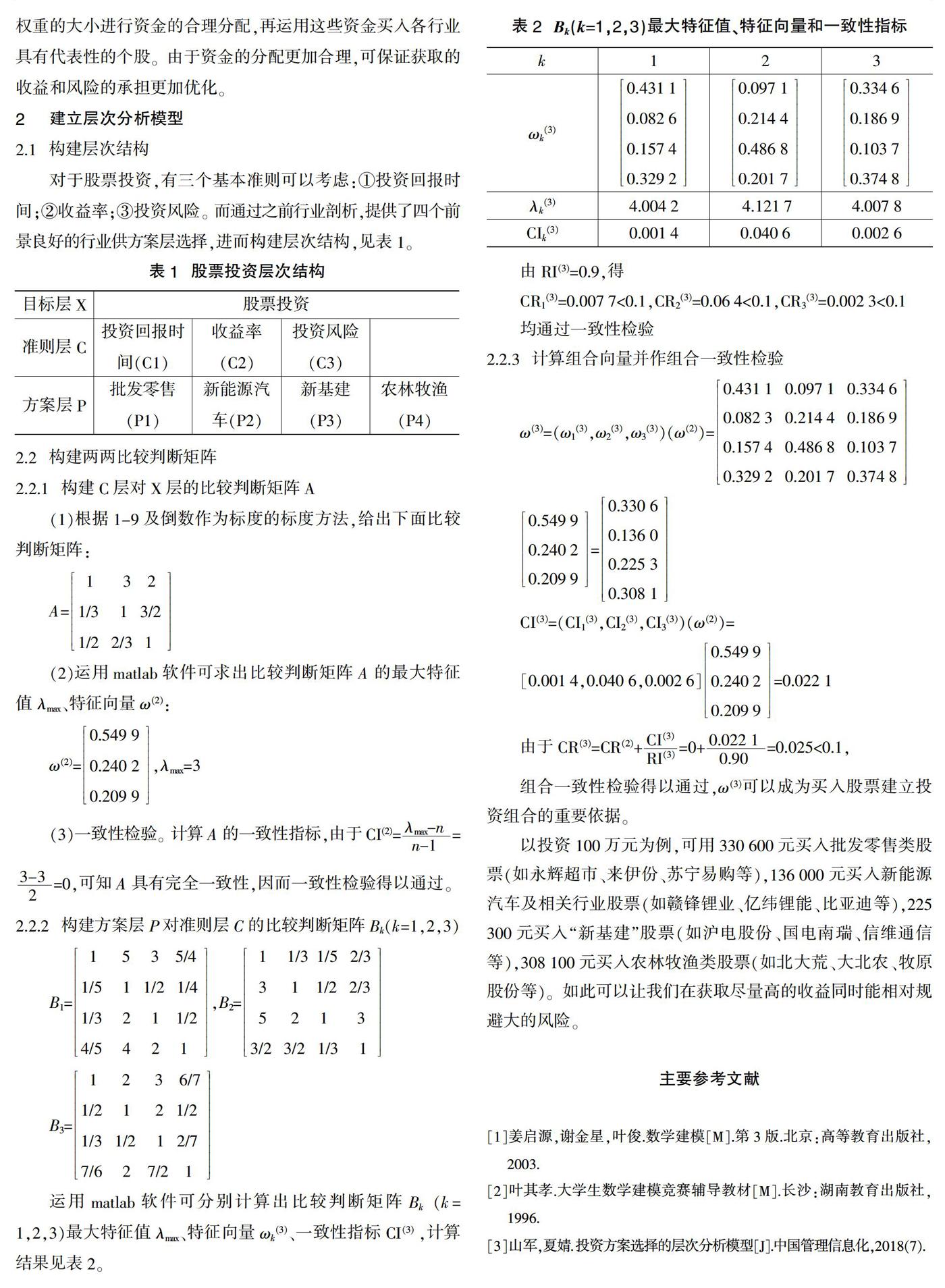
运用matlab软件可分别计算出比较判断矩阵Bk（k=1，2，3）最大特征值λmax、特征向量ωk（3）、一致性指标CI（3） ，计算结果见表2。

由RI（3）=0.9，得

CR1（3）=0.007 7<0.1，CR2（3）=0.06 4<0.1，CR3（3）=0.002 3<0.1

均通过一致性检验

2.2.3   计算组合向量并作组合一致性检验

ω（3）=（ω1（3），ω2（3），ω3（3））（ω（2））=0.431 1   0.097 1   0.334 60.082 3   0.214 4   0.186 90.157 4   0.486 8   0.103 70.329 2   0.201 7   0.374 8

0.549 90.240 20.209 9=0.330 60.136 00.225 30.308 1

CI（3）=（CI1（3），CI2（3），CI3（3））（ω（2））=

[0.001 4，0.040 6，0.002 6]0.549 90.240 20.209 9=0.022 1

由于CR（3）=CR（2）+=0+=0.025<0.1，

組合一致性检验得以通过，ω（3）可以成为买入股票建立投资组合的重要依据。

以投资100万元为例，可用330 600元买入批发零售类股票（如永辉超市、来伊份、苏宁易购等），136 000元买入新能源汽车及相关行业股票（如赣锋锂业、亿纬锂能、比亚迪等），225 300元买入“新基建”股票（如沪电股份、国电南瑞、信维通信等），308 100元买入农林牧渔类股票（如北大荒、大北农、牧原股份等）。如此可以让我们在获取尽量高的收益同时能相对规避大的风险。

主要参考文献

[1]姜启源，谢金星，叶俊.数学建模[M].第3版.北京：高等教育出版社，2003.

[2]叶其孝.大学生数学建模竞赛辅导教材[M].长沙：湖南教育出版社，1996.

[3]山军，夏婧. 投资方案选择的层次分析模型[J].中国管理信息化，2018（7）.