并行系统中排列图的可靠性近似算法

于中宝， 邵方明

（华东理工大学数学系，上海 200237）

并行系统提供了高速的运算潜力，但在高可靠性和容错性方面仍然存在问题，其原因与并行系统的网络拓扑有关，如超立方体，星图和排列图等。系统的可靠性定义为系统没有故障的概率，每个处理器正常运行的概率被记为p。排列图具有高容错性、直径小和低节点度等特点，因此进一步分析排列图的可靠性具有重要意义。

1 排列图的相关性质

1.1 排列图An,k 的定义[2]

n，k 都是整数，其中 1≤k＜n。

（1）点的定义：从{1,2,···, n}中取 k 个不同的整数得到排列 a1a2···ak，其中 ai=aj当且仅当 i=j。

（2）边的定义：排列图中的两点连接成边，当且仅当点（排列）中对应位置只有一个不同，比如节点 a1···ai-1aiai+1···ak和 a1···ai-1biai+1···ak的 第 i 个 位置不同，则这两个节点之间有边，其中1≤i≤k。图1中是以A4,2为例说明了排列图、子图和节点。

1.2 排列图子图的定义

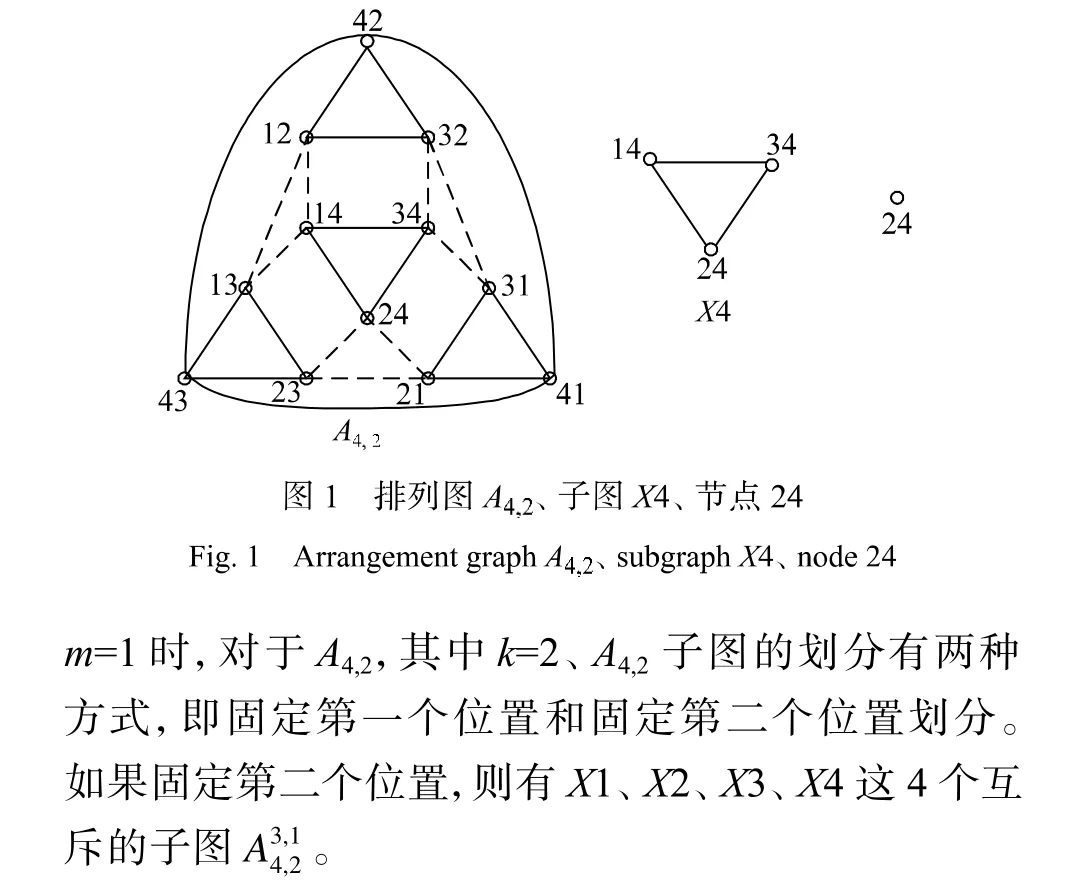
2 排列图子图可靠性的近似计算

排列图子图可靠性的计算是一个NP-hard 问题，所以可以用排列图子图可靠性的界去衡量排列图子图可靠性。

文献[1]已经给出上界的计算

（2）两个位置：因为从四个位置中选择两个位置放置symbol，所以位置的选择有 C42种。因为将4 个symbol 放置在两个位置上，有 3 种分法：(1, 3)、(2,2)和(3, 1)。(1, 3)表示取得的两个位置，第一个位置放 1 个 symbol，第二个位置放 3 个 symbol。(2, 2)表示取得的两个位置，第一个位置放2 个symbol，第二个位置放2 个symbol，(3, 1)表示取得两个位置，第一个位置放 3 个 symbol，第二个位置放 1 个 symbol，其所得结果和(1, 3)情况类似。

（3）三个位置：因为从四个位置中选择三个位置放置symbol，所以位置的选择有种。因为将4 个symbol 放置在三个位置上，有三种分法：(1, 1, 2)、(1,2, 1)和 (2, 1, 1)。(1, 1, 2)表示第一个位置放 1 个symbol，第二个位置放 2 个 symbol，第三个位置放2 个symbol。由排列组合知这三种分法所得结果一样，所以只对(1, 1, 2)讨论。

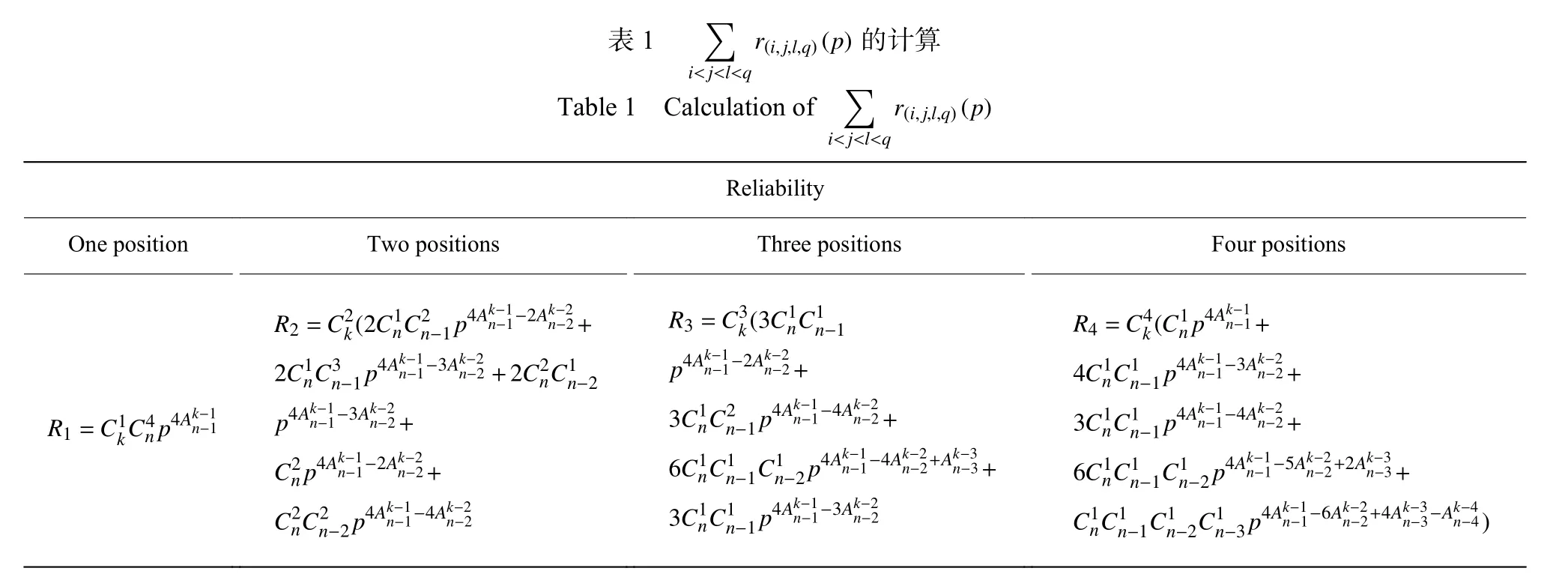
∑Table 1 Calculation of表 1 的计算∑r(i,j,l,q)(p)i＜ j＜l＜q r(i,j,l,q)(p)i＜ j＜l＜q Reliability One position Two positions Three positions Four positions R1=C1kC4n p4Ak-1 n-1 R2=C2k(2C1nC2n-1p4Ak-1 n-1-2Ak-2n-2+2C1nC3n-1p4Ak-1 n-1-3Ak-2n-2+2C2nC1n-2 p4Ak-1 n-1-3Ak-2n-2+C2n p4Ak-1 n-1-2Ak-2n-2+C2nC2n-2p4Ak-1 n-1-4Ak-2n-2 R3=C3k(3C1nC1n-1 p4Ak-1 n-1-2Ak-2n-2+3C1nC2n-1p4Ak-1 n-1-4Ak-2n-2+6C1nC1n-1C1 n-2p4Ak-1 n-1-4Ak-2n-2+Ak-3n-3+3C1nC1n-1p4Ak-1 n-1-3Ak-2n-2 R4=C4k(C1n p4Ak-1 n-1+4C1nC1n-1p4Ak-1 n-1-3Ak-2n-2+3C1nC1n-1p4Ak-1 n-1-4Ak-2n-2+6C1nC1n-1C1n-2p4Ak-1 n-1-5Ak-2n-2+2Ak-3n-3+C1nC1n-1C1n-2C1n-3p4Ak-1 n-1-6Ak-2n-2+4Ak-3n-3-Ak-4n-4)

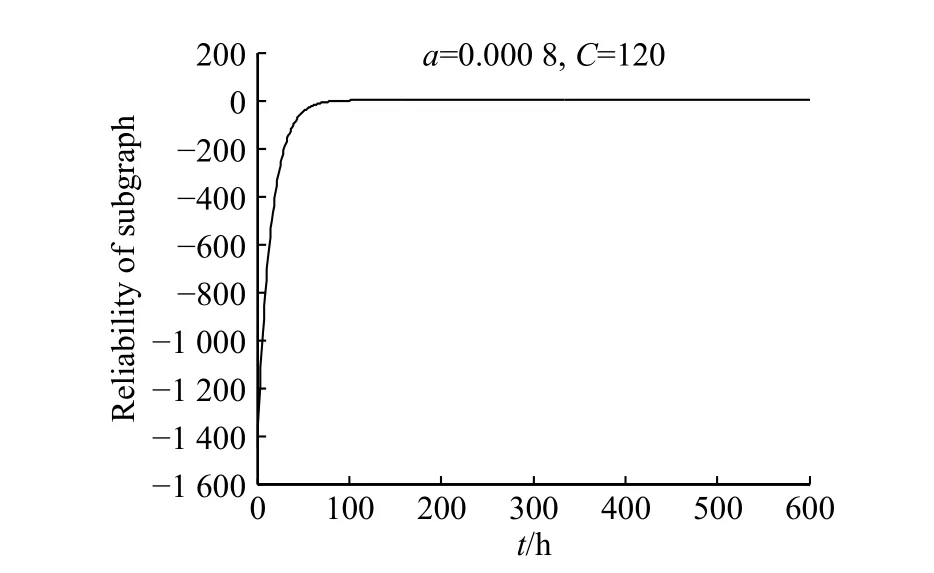
图 3 排列图A5,4 子图可靠性的近似计算Fig. 3 Approximate calculations of subgraph reliability of A5,4

针对鲁棒性的情况，本文提出了基于排列图的子图可靠性的蒙特卡罗算法近似计算排列图的子图可靠性。

3 蒙特卡罗方法计算排列图子图的可靠性

3.1 蒙特卡罗介绍

蒙特卡罗方法是以概率统计理论为指导的一种非常重要的数值方法，它使用随机数解决许多计算问题：

（1）输入最小值、最大值和最可能的估算数据，并为其选择合适的先验分布模型;

（2）根据以上输入，采用一定的规则，快速实施大量的随机抽样;

（3）对随机抽样的数据进行数学计算并处理结果;

（4）基于累积概率的分析，对结果进行概率分析，得出结论。

3.2 排列图子图的可靠性的蒙特卡罗近似计算

对于排列图An,k，排列图子图的可靠性定义为：当系统发生故障时，仍然存在一个正常运行子图的概率。

利用蒙特卡罗方法对排列图子图的可靠性进行计算的一般过程如下：

算法2：

（1）已知排列图An,k，输入循环次数N，节点正常运行概率p，计数器s=0；

（2）对于第i 次循环，生成(0, 1)之间的n!/(n-k)!个随机数，构成一个n!/(n-k)!维的向量γi；

（3）每个节点正常运行的概率为p，则失败的概率为q=1-p；若步骤(2)中向量γi的第j 个随机数大于q，记作对应的节点j 正常运行，状态变量记为1，否则记为0，得到状态向量λi；

（4）根据步骤(3)中λi状态，判断剩下正常运行的节点，是否构成一个排列图子图，如果构成一个排列图子图，则s+=1，否则s=s；

（5）如果 i≤N，i+=1，返步骤 (2)；否则，返步骤 (6)；

（6）可靠性为 s/N。

例2：以A3,2(图4)为例，对蒙特卡罗方法进行说明：

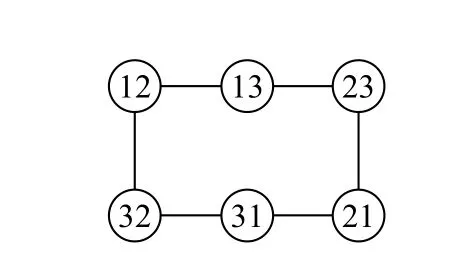
图 4 排列图A3,2Fig. 4 Arrangement graph A3,2

利用容斥原理，得到

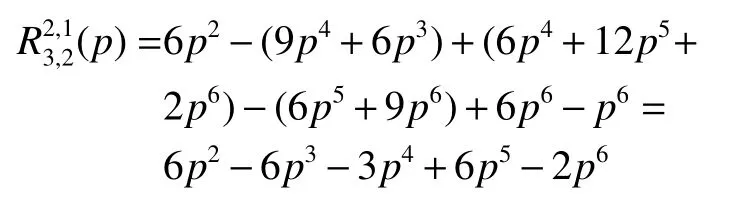
（1）输入循环次数 N=100，计数 s=0，p=0.8，q=0.2；

（2）随机生成一个6 维的向量(0.282 07, 0.136 92,0.438 19, 0.526 09, 0.065 82, 0.207 75)；

（3）生成状态向量 (1,0,1,1,0,1)；

（4）存在正常运行的子图X2(12, 32)和2X(23,21)，则 s+=1；

通过仿真计算，得到表2。

通过表2，发现蒙特卡罗得到的误差不足1%，而且随着循环次数的增多，误差越小。

表 2 A3,2 的子图可靠性蒙特卡罗近似计算Table 2 Approximate calculation of the Monte Carlo Method for A3,2 subgraph

4 实例验证

取p=0.85，N=1 000，得到An,k子图可靠性的界以及近似计算的结果见表3。

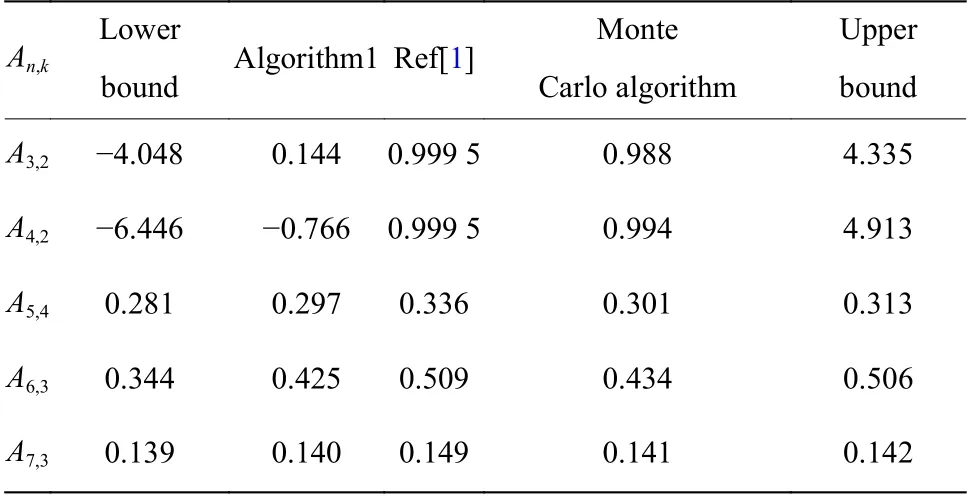
表 3 排列图An,k 子图可靠性的界以及近似计算（n=3,4,5,6,7；k=2,3,4）Table 3 Bounds and the approximate calculation of subgraph reliability for An,k（n=3,4,5,6,7; k=2,3,4）

通过表3 发现，A3,2、A4,2的上、下界出现了异常，这就是鲁棒性问题。对于A5,4、A6,3、A7,3，文献[1]中的近似值都大于上界值，而蒙特卡罗模拟的可靠性都在上、下界之间，可见蒙特卡罗模拟的可靠性结果要优于已知算法。

取p=0.5, 0.6, 0.7, 0.8, 0.9 得到排列图A3,2子图可靠性的近似解如表4 所示，结果表明算法1 的近似计算会出现鲁棒性问题，已有近似计算的结果要大于真实值，利用蒙特卡罗得到近似结果和真实值基本重合。

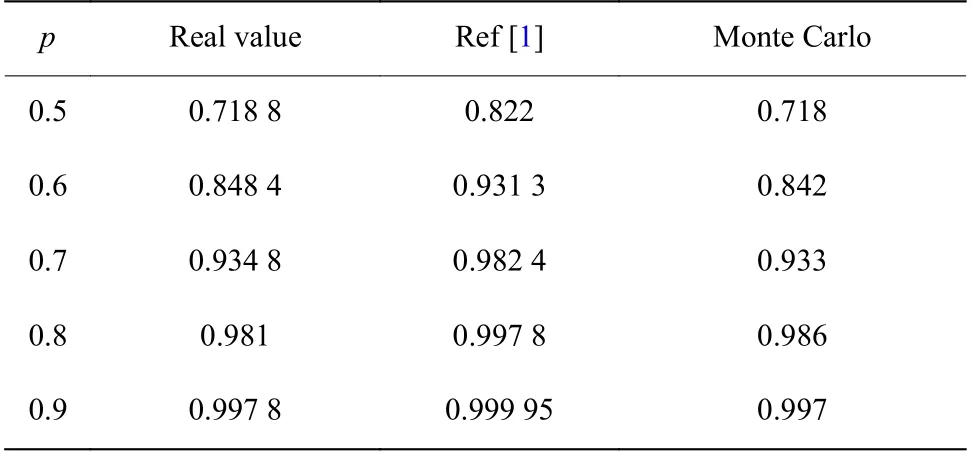
表 4 排列图A3,2 子图可靠性的近似计算Table 4 Approximate calculation of subgraph reliability for A3,2

5 结 论

本文主要研究了排列图子图的可靠性问题，提出了排列图子图的下界，在此基础上提出了算法1：将上、下界的平均值作为排列图子图可靠性的近似值。在算法1 的计算过程中会有鲁棒性问题，针对这一问题，本文提出了基于排列图的蒙特卡罗模拟算法，利用蒙特卡罗去计算A3,2的排列图子图的可靠性，其误差不足1%。对于其他排列图的可靠性，蒙特卡罗算法也优于已知的近似算法。