煤气化装置中的粉煤流量调节阀数值模拟研究

2020-12-23陈美华陆海峰郭晓镭

华东理工大学学报(自然科学版) 2020年6期

陈美华，陆海峰，郭晓镭，龚欣

（华东理工大学上海煤气化工程技术研究中心，上海 200237）

煤气化技术是煤化工中实现煤炭清洁高效利用的重要手段[1-2]。在粉煤气化工艺中，粉煤管线的稳定对工艺指标、气化效率等起到至关重要的作用[3]。为满足气化炉在不同负荷下运转的需求，需要相应地调整入炉煤量和氧量。在国内外粉煤气化工艺上，一般都采用粉煤流量调节阀来调节粉煤流量[4-5]。然而，由于粉煤输送单元中阀门操作条件恶劣、阀门动作频繁，煤化工中阀门极易损坏，制约了煤气化装置的长周期运行[6-7]。人们在对该调节阀的性能及其在粉煤输送系统中的作用等方面的研究、分析还很不够，尤其对调节阀内部气固两相流动特征的研究鲜见报道。

在已有的文献报道中，研究者们大多借助实验的手段开展粉煤流量调节阀特性研究。例如，熊焱军等[8]研究了3 种不同结构阀芯的粉煤调节阀的性能。林雯等[9]对Shell 煤气化装置中粉煤调节阀性能进行研究，发现粉煤调节阀在开度40%左右已达到满负荷。王洁等[5]对失效的粉煤调节阀解体得知该阀出现的主要问题是阀内件易被冲损。实际流动过程中，颗粒、流体、管壁之间的碰撞和摩擦十分剧烈，导致阀内压力和流速剧烈变化[10-11]，然而传统的实验方法只能获得流量和压力信号[8-9]，无法对阀门流动特征进行分析。数值模拟方法是目前研究流体内部流动特征的主流方法，通过数值模拟可以获取大量实验都无法测量的详细信息[12]。因此，本文拟借助数值模拟的手段开展调节阀内部流场特性研究，以了解气固两相流经阀门时的内部情况，为调节阀的结构设计、工艺操作控制等提供借鉴。

气固两相的数值模拟方法主要有欧拉-欧拉模型和欧拉-拉格朗日模型。欧拉-欧拉模型[13]将固相颗粒视为拟流体，用平均颗粒粒径代替粒径分布会导致较大的计算误差；传统的欧拉-拉格朗日模型例如离散元方法(Discrete Element Method，DEM)[14]虽然适合较宽范围颗粒形状、粒径和速度，但其计算效率受计算颗粒数量限制，难以应用于实际操作和连续计算。计算颗粒流体动力学(CPFD)是基于多相质点网格法 (Multiphase Particle-in-Cell Model，MP-PIC)提出[15-16]，本质上属于欧拉-拉格朗日模型。在CPFD 计算中，数值计算的颗粒不是物理意义上的颗粒，而是将具有相同密度、温度、尺寸等属性的颗粒打包为“计算颗粒(Computational Particle)”，从而使得CPFD 能够处理包含数亿个粒子的气固系统[17]。此外，CPFD 方法中采用了实际的颗粒粒径分布，将气固两相间的相互作用描述得更真实[18]。

本文利用CPFD 数值模拟方法对包含数亿个粒子的气固两相系统的工业规模粉煤流量调节阀进行研究，首先探究了CPFD 方法在该三维气固两相模拟中的适用性；然后基于CPFD 方法预测不同开度下粉煤流量，获得阀门流量特性曲线；最后着重分析了不同开度下阀门的流动特性参数。

1 实验及模拟条件

1.1 实验装置

气化炉运行时，煤粉输送系统的总压降约为0.9 MPa，粉煤调节阀压降占输送系统总压降的70%～80%，是该输送系统的重要阻力部件[19]。粉煤流量调节阀为角式调节阀，如图1(a)所示。进口垂直向下，进出口夹角为120°。阀芯是粉煤调节阀的关键部位，如图1(b)所示。阀芯为杯口状，侧壁开槽。粉煤颗粒进入阀门后垂直落入阀芯杯口，然后通过侧壁的斜槽流出阀门，阀芯上下移动改变节流面积，从而改变粉煤流量[20]。

1.2 实验工况及实验物料

表1 给出了气化炉在满负荷和60%负荷条件下运行的工况数据。满负荷状态是指气化炉的煤粉处理能力达到设计值的状态。本文研究的粉煤气化装置的气化压力大约为4.0 MPa，气化炉的煤粉处理能力为2 000 t/d，需要4 路煤粉输送管线同时输送，因此在气化炉满负荷状态下单路管线的煤粉输送量约为20 t/h。由表1 见，在粉煤气化装置上40%开度下调节阀基本达到满负荷状态，16%开度为调节阀受供氧量制约而保持的常开状态，对应约70%(质量分数)气化炉负荷[19]。

煤气化装置的气化用煤为混配煤，添加质量分数4%石灰石作为助熔剂。通过真密度分析仪(Accupyc 1330 pycnometer, Micromeritics Instrument Corporation 公司)测得颗粒密度为1 400 kg/m3。通过粉体特性测试仪(PT-X, Hosokawa Micron Corporation公司)测得粉煤松装密度为525 kg/m3，振实密度为982 kg/m3，通过马尔文激光粒度仪(Malvern 2000 MU,Malvern Panalytical 公司)测得粉煤的体积平均粒径为48 μm，粉煤粒径的分布曲线见图2。

1.3 模拟设置

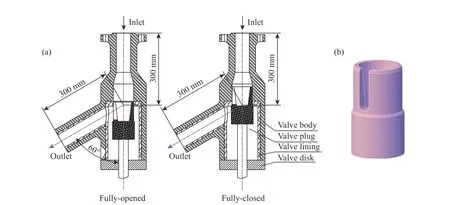
图 1 (a) 粉煤流量调节阀结构；(b) 阀芯的几何模型Fig. 1 (a) Structure of regulating valve for pulverized coal; (b) Geometric model of the valve plug

表 1 气化炉在满负荷和60%负荷条件下的工况条件Table 1 Operation conditions gasifier under full load and 60% (mass fraction) load

图 2 粒径分布曲线Fig. 2 Curve of particle size distribution

依据图1 给出的调节阀结构建立如图3 所示的三维流道模型，用于粉煤调节阀的气固流动特性数值模拟研究。定义阀门全关时的行程为0 mm，阀门开启后阀芯向下运动，16%和40%的开度分别对应的阀芯下移距离为10.2 mm 和25.6 mm。粉煤流量调节阀出口设置了1 000 mm 的直管段，用于研究粉煤流经调节阀后的气固流动特性。调节阀模型的主要结构参数和材料参数设置分别见表2 和表3。经无关性验证后选取6×105网格用于数值计算。数值计算的初始和边界条件如下：(1)初始条件：输送前给料罐的出料阀关闭，管道内部均匀充满高压氮气，其表压约为4.60 MPa。(2)边界条件：阀门入口定义为入口流动边界，进口粉煤输送量见表1；直管末端定义为出口压力边界，出口压力由发料罐压力和调节阀压降的差值得到。计算时间步长为0.000 1 s。

2 结果与讨论

2.1 模型验证

图 3 粉煤流量控制阀的几何模型Fig. 3 Geometric model of regulating valve for pulverized coal

表 2 粉煤调节阀模型的主要结构参数Table 2 Main structural parameters of regulating valve model for pulverized coal

表 3 模拟材料参数设置Table 3 Material parameters setting for simulation

为了验证CPFD 数值模拟对粉煤调节阀气固两相流动过程的有效性，本研究对表1 所给出的工况展开数值模拟研究，并对调节阀压降、粉煤速度和粉煤质量浓度与表1 给出的相应工业数据进行对比，结果见图4。首先在宏观上对调节阀压降结果进行对比，模拟所得调节阀压降与实验的最大误差为17.5%。图4 同时也给出了稳定输送时调节阀出口处粉煤速度和粉煤质量浓度的对比结果。由图可知在模拟达到稳定输送时，粉煤速度和粉煤质量浓度模拟结果偏差在±5.0%误差范围内，说明通过CPFD 数值模拟可以获取粉煤颗粒流经调节阀过程的微观流动信息。综上，CPFD 数值模拟适用于模拟粉煤流经流量调节阀的气固两相流动过程，并且能有效预测管内的颗粒流速和粉煤质量浓度，但是对压降的预测结果误差相对较大，进一步说明调节阀内部流动研究的重要性。

图 4 模拟值与实验值比较Fig. 4 Comparison between simulated and experimental values

2.2 流量预测

调节阀的流量特性是调节阀的重要参数之一，为了对粉煤流量调节阀的流量特性进行预测，建立了图5 所示的计算框图，具体计算步骤为：

(1) 计算开始时，给定开度、进口压力Pi(即给料罐压力)，并基于文献[19]实验中获得的调节阀压降特性曲线(调节阀的压降与开度的关系为ΔP=4.17e-0.078x，其中 ΔP 为调节阀的压降 (MPa)，x 为阀门开度(%))得到调节阀压降ΔP；

(2) 假定粉煤的初始质量流量为mi，利用验证后的CPFD 模型展开数值模拟，获得调节阀的出口压力Po和调节阀压降|Pi-Po|；

利用图5 所示的计算框图对10%～40%开度的调节阀展开流量预测，预测结果见图6。由图6 可知，随着调节阀开度的增大，粉煤输送量也随之增大。这是因为调节阀开度增大对应着流动通道增大，流动阻力减小。CPFD 数值模拟的粉煤流量预测结果随开度变化趋势与实际工业中调节阀随开度的变化趋势相同，但粉煤流量预测值略小于实验值，误差范围在10%以内。预测偏差的缘由可能是：(1)实际过程中阀门压降与开度、气体流量之间存在一定的关联性，调节阀压降ΔP 并不能简单处理；(2)气固两相介质的调节阀对固体流量的调控作用较为复杂，在模拟中做了一些简化(阀门的三维模型简化、边界条件的简化等)。

图 5 流量预测计算框图Fig. 5 Calculation block diagram of mass flow rate prediction

图 6 粉煤流量调节阀流量特性Fig. 6 Flow rate characteristics of regulating valve for pulverized coal

2.3 阀门内部流动特征

图 7 阀门的沿程压力图Fig. 7 Pressure diagram along the valve

图7 示出了16%和40%开度下阀门内部的沿程压力信号。图中Distance 表示颗粒在阀门内经过的距离，0 mm 表示阀门入口截面，600 mm 表示阀门出口截面，1 600 mm 表示阀门下游管道出口截面。由图可知：不同开度下阀门沿程压力变化趋势大致相同：在入口段压力较大，压力的波动主要与管道截面相关，随着流体进入阀芯区域，压力逐渐降低；在阀芯出口处，压力骤减，随后逐渐回升，压力骤减是因为经过阀芯节流面时，粉煤速度变化和因颗粒撞击阀芯内壁导致的巨大能量损耗由压力提供。

图8 出了16%和40%开度下阀门的沿程粉煤速度和颗粒体积分数分布。对比其粉煤速度信号可知：16%开度下粉煤速度的最高值为49.7 m/s，其速度变化量最大的区域宽度S1约为262.4 mm，40%开度下粉煤速度的最高值为29.1 m/s，其速度变化量最大的区域宽度S2约为383.3 mm。这说明低开度下速度变化率较大、区域集中，易对局部区域产生较大的应力。对比其颗粒体积分数可知：16%开度下在阀门出口段距离（300～600 mm）出现两处间隔距离较远的颗粒体积分数高峰值，而在稳流管段中颗粒体积分数一直在逐渐减小；而40%开度下在阀门出口段距离（300～600 mm）存在一段颗粒体积分数较高位置，在稳流管段中颗粒体积分数先减小，随后逐渐达到稳定。在低开度下，颗粒体积分数有两处达到高峰值原因是：靠近阀芯出口处是因为速度较大造成的颗粒挤压效果，而远离阀芯出口处是因为粉煤速度减小，颗粒在管道上壁形成堆积效应。对比调节阀下游直管段内沿程粉煤速度信号和颗粒体积分数分布可以发现，低开度下颗粒在下游直管段出口附近达到稳定，高开度下颗粒在下游直管段中心位置左右达到稳定。

图 8 阀门的沿程粉煤速度、颗粒体积分数图Fig. 8 Coal velocity and particle volume fraction along the valve

图9 示出了16%和40%开度下阀门内部流动特征云图。由图9(a)可知，粉煤速度变化较大的主要集中在阀芯节流口位置，低开度下节流口处粉煤速度明显较高，且在很大的区域范围内，粉煤速度在30.0 m/s 以上，而高开度下阀芯节流口位置粉煤速度基本上在30.0 m/s 以下，这说明调节阀发生磨损的位置在阀芯出口和斜管交界处位置，磨损原因是调节阀长期处于低开度下受高速粉煤颗粒撞击磨蚀。颗粒在阀芯节流口后方有明显的回流现象；在低开度下颗粒的回流较为集中，回流的粉煤速度较高，而在高开度下颗粒的回流较为发散，回流的粉煤速度较低；低开度下的下游直管内粉煤速度变化情况较为复杂，需要更长的距离才能使管道粉煤速度分布达到较为稳定的状态。由图9(b)可知：回流区域中的颗粒体积分数较低，说明仅有少部分颗粒发生回流；低开度下的下游直管内颗粒的流动较为复杂，需要较长的距离才能使管道粉煤速度分布达到较为稳定的状态，综合考虑平均时间段内的粉煤速度和颗粒体积分数分布，为使下游管道颗粒达到较为稳定流动，其下游管段至少为800 mm。