全断面岩石掘进机刀间距研究方法的发展与分析

华北电力大学能源动力与机械工程学院 北京 102206

刀盘作为全断面岩石掘进机 (Full Face Rock Tunnel Boring Machine，TBM)的关键部件，其上一般安装数十把甚至上百把破岩盘形滚刀。盘形滚刀在刀盘上的布置参数——刀间距和相位角是影响 TBM作业效率的关键参数，尤其是刀间距[1]。自 Teale[2]于1965 年提出刀具切割单位体积岩石所消耗的能量为比能的概念起，便一直为学者广泛关注。L.Ozdemir 等人在其研究报告[3-4]中曾发现刀间距与比能的关系，并提出刀间距从某一值减小时，会使岩石碎片尺寸变小，从而比能增大；而当刀间距从此值逐渐增大时，破岩刀具间的相关性减弱直至消失，比能也随之增大，此刀间距即为最佳刀间距Sopt，其对应的比能为最小。对于如何确定最佳刀间距，国内外学者进行了盘形滚刀的压痕试验、盘形滚刀线性滚压破碎 (切割)岩石试验和盘形滚刀圆形滚压破碎岩石试验。随着计算机技术的应用和发展，为盘形滚刀最佳刀间距的研究提供了新选择——数值模拟，但其基本依据仍然是盘形滚刀的压痕、线性滚压和圆形滚压破碎岩石试验的基本方法。该研究方法与 TBM 实际作业间存在何种关系，哪种研究方法更合理，其合理性如何度量，这些问题尚未有明确结论。

在TBM 在我国规模化发展和应用的今天，通过对盘形滚刀在 TBM 刀盘上布置的关键参数——刀间距S的确定方法进行梳理，发现刀间距不同确定方法的优缺点，尤其与盘形滚刀实际破岩间的关系，进而改进或更客观、更全面地确定 TBM 刀盘上盘形滚刀布置的最佳刀间距，必将为 TBM 设计理论的发展和完善提供重要参考。

1 盘形滚刀破岩分析

TBM 刀盘上盘形滚刀的滚动破岩是在刀盘推力作用下，盘形滚刀侵 (贯)入岩石一定深度h，在随刀盘旋转的同时自转并滚压破碎岩石的过程。因此，就TBM 刀盘上盘形滚刀的破岩运动而言，所有盘形滚刀都作同心圆形轨迹滚压破岩。就刀盘上安装半径为Ri的第i把盘形滚刀而言，其破岩过程如图 1 所示[5]。图 1 中E为破岩前锋点，F为最大贯入度点，弧EF为盘形滚刀破岩刃，P为盘形滚刀贯入度，ωi为第i把盘形滚刀旋转角速度，FN为法向推力。

图1 盘形滚刀破岩示意Fig.1 Sketch of rock breaking with disc cutter

就盘形滚刀刃上的点E而言，在盘形滚刀转过 1圈的过程中完成了 1 次破岩，亦即，盘形滚刀刃上任一点都具有此特点——间歇性周期破岩。E点与F点之间接岩弧段EF称为破岩刃，则该刃段也具有间隙破岩特点。在盘形滚刀破岩力作用下，其破岩刃作用于岩石上并引起岩石变形、传递应力，进而引起岩石内部的裂纹产生、失稳扩展等变化。一般而言，该过程极其复杂，很难定量描述 (见图 1(b))。由于盘形滚刀随刀盘的公转，其破岩点 (如E点)至最大贯入度的过程中还发生垂直于盘形滚刀刃所在平面的运动 (如E点运动到E′)——侧滑 (见图 1(c))。

由于 TBM 刀盘上一般安装数十把甚至上百把破岩盘形滚刀，这些盘形滚刀在刀盘上的布置一般要考虑其综合破岩效果好，即破碎单位体积岩石所消耗的能量最小。实现此破岩效果的关键就是使 TBM 刀盘上布置的盘形滚刀作用下的岩石内部便于产生裂纹并失稳扩展，相邻盘形滚刀间的裂纹便于贯通，从而产生尽可能多的块状 (大块)岩碴，如图 2 所示。显然，影响产生此种结果的重要参数就是相邻盘形滚刀间的距离，即相邻盘形滚刀轨迹圆在刀盘半径上的距离——刀间距S。如图 2(a)所示，刀间距SL过大，刀盘旋转 1 周，相邻盘形滚刀间的岩石内部产生的裂纹不能贯通，从而在这 2 个盘形滚刀间形成岩脊，致使后续掘进抗力增加，破岩效果下降；如图 2(b)所示，刀间距SS过小，刀盘旋转 1 周，相邻盘形滚刀间的岩石内部产生的裂纹多次贯通，生成的岩碴较小，岩石发生过度破碎现象，能量消耗较大；如图 2(c)所示，刀盘旋转 1 周，在 2 个相邻盘形滚刀最大贯入度点产生的裂纹刚好贯通，形成整块碎断体 (大块)岩碴，盘形滚刀破岩能量充分发挥，产生了极佳破岩效果，此刀间距就是最佳刀间距Sopt。

图2 盘形滚刀刀间距与破岩效果Fig.2 Disc cutter spacing and rock breaking effects

2 刀间距的确定方法

通过盘形滚刀的破岩分析发现，盘形滚刀破岩的直接作用就是使其能够贯入岩石，而实现这一效果的直接方式就是压痕试验，因此，研究盘形滚刀破岩的最早试验方法就是盘形滚刀的压痕试验。盘形滚刀连续破岩的直接方式是盘形滚刀线性 (平面运动)滚压破碎岩石，而盘形滚刀的连续循环破岩则是其圆形滚压破碎岩石，这也是 TBM 盘形滚刀实际破岩采用的方式。上述研究方法所对应的盘形滚刀与岩石的相互作用关系如图 3 所示。

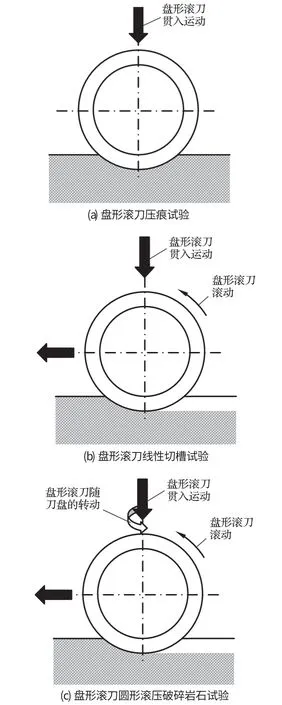
图3 试验方法及盘形滚刀与岩石的作用关系Fig.3 Relationship among test method,disc cutter and rock

由图 3(a)可以看出，压痕试验盘形滚刀只有贯入岩石的运动。若以盘形滚刀刃所在平面进行分析，则盘形滚刀与岩石的相互作用关于此平面依概率 (考虑岩石性能的离散性和不均匀性)对称；若以通过盘形滚刀最大贯入度点且垂直于盘形滚刀刃所在平面的平面进行分析，同样可得出盘形滚刀与岩石的相互作用关于此面仍依概率 (考虑岩石性能的离散性和不均匀性)对称的结论。因此，当对盘形滚刀的破岩上升到理论分析的时候，其压痕试验所对应的盘形滚刀具有一维运动属性，亦即用此方法研究盘形滚刀刀间距称为刀间距的一维确定方法。

图3(b)给出了线性滚压破碎岩石过程中盘形滚刀与岩石的作用关系，仍以盘形滚刀刃所在平面进行分析，则盘形滚刀与岩石的相互作用关于此平面依概率 (考虑岩石性能的离散性和不均匀性)对称；若以通过盘形滚刀最大贯入度点且垂直于盘形滚刀刃所在平面的平面进行分析，则盘形滚刀与岩石的相互作用关于此面不具有概率对称性。因此，当对盘形滚刀的破岩上升到理论分析的时候，其线性滚压破碎岩石的试验所对应的盘形滚刀具有二维运动属性，用这种方法研究盘形滚刀刀间距称为刀间距的二维确定方法。

图3(c)给出了圆形滚压破碎岩石过程盘形滚刀与岩石的作用关系，无论以盘形滚刀刃所在平面，还是以通过盘形滚刀最大贯入度点且垂直于盘形滚刀刃所在平面的平面进行分析，盘形滚刀与岩石的相互作用均不具有概率对称性。因此，当对盘形滚刀的破岩上升到理论分析的时候，其圆形滚压破碎岩石的试验所对应的盘形滚刀具有三维运动属性，以这种方法研究盘形滚刀刀间距称为刀间距的三维确定方法。进一步对比还可发现，盘形滚刀线性滚压 (二维)破碎岩石相当于安装半径为无穷大的盘形滚刀的圆形滚压 (三维)破碎岩石。这样就可方便看出盘形滚刀的压痕试验、线性切槽试验和圆形滚压破碎岩石试验间的区别和联系。

当然，TBM 最优刀间距的确定也可根据其来源不同分为室内试验、工程经验和软件模拟。其中室内试验确定最优刀间距的方法已如前述，即盘形滚刀的压痕、线性切槽 (滚动)和圆形滚压破碎岩石的试验；而工程经验则是根据大量 TBM 施工工程数据的统计分析，推测不同地质条件下的最优刀间距；软件模拟则是计算机技术在最优刀间距确定领域的应用。目前，室内试验仍是确定 TBM 最优刀间距的常用方法。而将 TBM 刀间距区分为一维、二维和三维确定方法，既是根据室内试验确定盘形滚刀与岩石的相互作用关系，也为将盘形滚刀的安装参数 (安装半径和相位角)引入最优刀间距的确定奠定了理论基础，将进一步推进最优刀间距确定方法的发展。

2.1 刀间距一维确定方法

2.1.1 历史背景

人们最早破碎岩石的方法就是凿岩、钻眼等，先将工具侵入岩石，然后使其周围的岩石大块崩落。考虑到岩石的硬度和抗压强度一般都很大 (俗语说“硬如顽石”)，因此，TBM 盘形滚刀破岩，首要且关键的问题也是让其贯入岩石一定深度。20 世纪中叶，研究者们也是认为将盘形滚刀垂直贯入岩石是盘形滚刀破碎岩石最主要和最直接的方法，这就是刀间距一维确定方法产生的历史背景。由于岩石的多样性、内部结构的复杂性和性能的离散性，刀间距一维确定方法基本是盘形滚刀的室内压痕试验。

2.1.2 室内压痕试验

室内压痕试验是 20 世纪 70、80 年代研究 TBM刀盘上刀间距的基本方法，属于刀间距的一维确定方法，又称为压头贯入试验，即在盘形滚刀刃上截取一小段作为压头侵入岩体进行试验，试验原理[6]如图 4 所示。当时应用的盘形滚刀刃一般为楔形刃[7](见图 5)，因此，试验用压头一般也为楔形刃压头，即从盘形滚刀楔形刃上截取一段焊接在压头座上[8](见图 6)。室内压痕试验装置相对简单，主要设备为一台万能材料试验机，试件一般为放入圆形钢模中的正四棱柱体，正四棱柱体与圆形钢模之间的间隙用高标号水泥按一定配比制成的混凝土填充，以模拟无限大岩面[8]，如图 7 所示。图 7 中，①、② 和 ③为压痕顺次，则第 1 次压痕，压头两侧的刀间距皆为无穷大；第 2 次压痕一侧为无穷大，另一侧为 2 倍刀间距；第3 次压痕，压头两侧皆为刀间距。

图4 盘形滚刀压痕试验原理Fig.4 Principle of disc cutter indentation test

图5 盘形滚刀楔形刃Fig.5 Wedge edge of disc cutter

图6 压头及应变片布置Fig.6 Layout of indenter and foil gauge

图7 压痕试验试件Fig.7 Specimen of indentation test

因此，压痕试验对设备要求低，并且在一定范围内有效，尤其是预测盘形滚刀推力与其贯入度间的关系方面具有一定优越性能，故目前该试验方法仍在使用。

2.1.3 软件模拟

计算机技术的发展，使得盘形滚刀与岩石相互作用关系的研究进入了数字时代。在刀间距一维确定方法中，有学者采用离散元方法建模，模拟盘形滚刀作用下岩石裂纹的扩展和连通情况[9](见图 8)。数值模拟可直观研究最优刀间距，即当且仅当 2 把滚刀下的裂纹恰好连通，盘形滚刀破岩能耗最小，TBM 的破岩效率最高，此时的刀间距为最优刀间距。

图8 滚刀侵入模型Fig.8 Disc cutter penetrating model

起初，文献 [9]和 [10]只是应用软件探讨最优刀间距和贯入度之间的关系；之后发现，工程实际中刀盘上盘形滚刀破碎岩石通常是多把滚刀顺次作用的过程。因此，文献 [11]和 [12]开始研究盘形滚刀作业顺次对破岩效果的影响，并发现盘形滚刀的顺次作业能提高其破岩效率，但基本不影响最优刀间距。再之后，学者认识到了岩体的复杂性，模拟开始考虑岩性[13]、节理倾角及间距[14]、围压[15-16]等对最优刀间距的影响，并取得了一定成果。其中，文献 [16]使用颗粒流分析软件 PFC2D 建立双滚刀侵入破岩模型，滚刀模型的刃宽为 10 mm，刀刃角为 20°，刀刃上的过渡圆弧半径为 4 mm，破岩对象定义为花岗岩，选用接触粘结模型来模拟颗粒之间的接触关系。根据TBM 真实掘进地层中可能出现的围压值，设定岩石两侧的围压分别为 1、5、10、15、20、25 MPa，刀间距分别为 60、70、80、90、100 mm，设定侵深为10 mm，模拟双刃中心滚刀在不同围压与刀间距下的侵入破岩过程。通过计算分析不同工况下的比能，发现当围压为 1～10 MPa 时，最优刀间距约为 70 mm；当围压增加到 15～20 MPa 时，最优刀间距约为 80 mm；当围压为 25 MPa 时，最优刀间距约为 85 mm。

2.2 刀间距二维确定方法

2.2.1 历史背景

随着 TBM 的应用和普及，尤其是 20 世纪 60 年代至 80 年代，西方发达国家基础建设进入高潮，如交通隧道、引输水隧洞等岩石质地层广泛采用 TBM 施工，曾一度出现研制 TBM 的公司，如美国的 Robbins、Jarva 和德国的 Demag、Wirth 四强并列的局面。期间也是 TBM 在西方发达国家大发展并逐渐完善的时期。TBM 工程应用中出现的盘形滚刀寿命低，尤其是磨损后的盘形滚刀破岩效能急剧降低的现象，使人们认识到了盘形滚刀破岩一维研究的局限性，这就是盘形滚刀线性滚压破碎岩石试验装置的研发背景。

2.2.2 室内试验

二维确定刀间距的典型试验是盘形滚刀线性滚压破碎岩石试验，也是目前国内外多数研究机构采用的室内盘形滚刀破碎岩石试验，其试验原理和试验装置[17]如图 9 所示。在该领域，最早进行盘形滚刀线性滚压破碎岩石的试验由美国 Colorado School of Mines 的学者 L.Ozdemir 等人于 1979 年完成，所建立的模型被称为 CSM 模型，其后进行过多次完善，并于 2007 年进行的盘形滚刀线性滚压破碎 Colorado Red Granite 试验中发现最优刀间距为 76 mm。

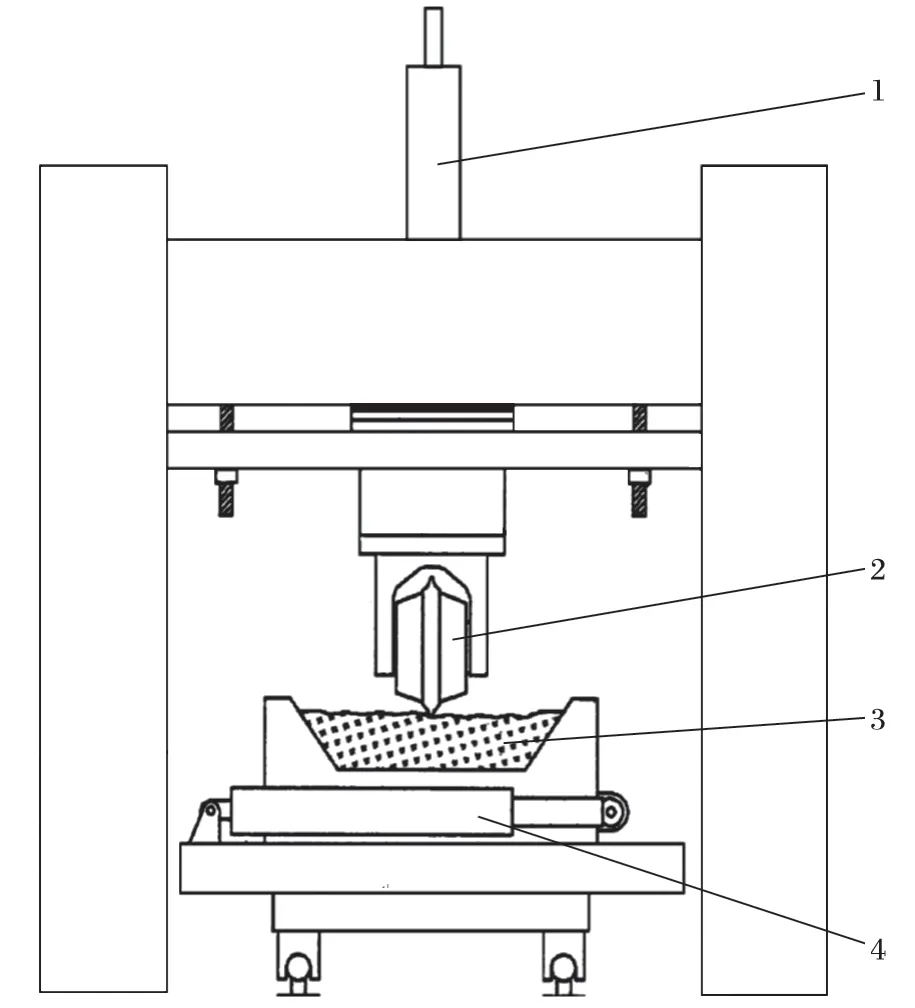
图9 盘形滚刀线性滚压破岩试验装置Fig.9 Disc cutter linearly rolling and breaking rock test device

由于场地、成本等的限制，难以实现对刀盘上多把盘形滚刀的室内滚压破碎岩石的试验，因此在室内进行单把盘形滚刀线性滚压破碎岩石的试验成为主流。其中，全尺寸盘形滚刀线性破岩试验由于在试验中采用大体积岩石，可以避免尺寸效应的影响而被广泛应用。起初，国内外学者采用盘形滚刀线性滚压破碎不同的岩石来进行全尺寸盘形滚刀线性破岩试验，以此来研究最优刀间距和贯入度之间的关系[18-19]，发现贯入度对最优刀间距有着很大的影响。随着人们对最优刀间距认识的不断加深，学者们把研究方向集中在外界环境参数及刀具自身参数对最优刀间距的影响上，如盘形滚刀刃宽[20]、载荷特点[21](静载、动静组合加载)、干燥和饱水条件[22]等，尽管这些因素对盘形滚刀的破岩效率有一定影响，但对最优刀间距影响不大，甚至可以忽略。而岩石温度会对最优刀间距产生影响，最优刀间距会随着岩石温度的升高而增加[23]。

2.2.3 软件模拟

因为刀间距的二维确定方法必须用三维模型实现，而三维离散元软件计算量非常大，所以在建模过程中，经常采用的方法为有限元，所用软件以ABAQUS 和 ANSYS 为主，也有部分学者采用离散元方法。

国内外学者建模大都只保留盘形滚刀的刀圈和刀体，并以此模拟盘形滚刀线性滚压破碎岩石的过程[24]，如图 10 所示。文献 [25]采用三维颗粒离散元方法分析不同断面形态下岩石裂缝扩展的范围，以及不同刀间距下破岩比能与贯入度的关系，发现刀间距与贯入度的比值为 10 时比能为最小值，此时破岩效率最高。文献 [26]采用三维接触算法的离散元软件 MatDEM 建立了 TBM 双滚刀线性顺次切割模型，发现当S/P(刀间距/贯入度)=20～25 时，破岩比能最小。文献 [18]和 [27]应用盘形滚刀线性滚压破碎岩石的试验数据，采用三维有限元方法的 ANSYS 平台研究了如何确定盘形滚刀最优刀间距。其中，文献[27]使用有限元仿真分析软件 ANSYS AUTODYN 建立单把滚刀线性破岩模型，滚刀直径为 432 mm 的 V形刀具。在给定贯入度下，该 V 形刀具与作业对象的接触宽度与直径为 432 mm 等截面盘形滚刀的接触宽度相同。线性滚压破碎和模拟岩石类别及性能如表 1所列。模拟采用 Drucker-Prage 岩石本构模型，模拟贯入度为 4 mm，发现线性滚压破碎上述岩石，当比能最小时的S/P分别为 11、13、10、10、10、14、10、15。

图10 线性滚压破岩模拟Fig.10 Simulation of linear rolling and breaking rock

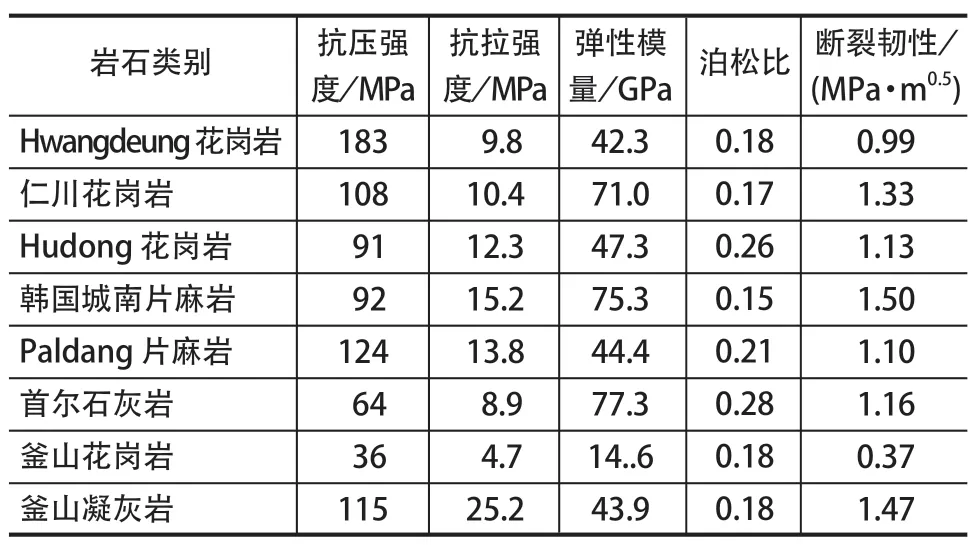
表1 线性滚压破碎和模拟岩石的类别及性能Tab.1 Classification and properties of rocks used for linear rolling and breaking rock simulation

文献 [28]通过建立 2 把盘形滚刀线性滚压破碎岩石的模型，并将模型得到的切向力和比能值与其线性滚压破碎岩石的试验数据进行对比，发现两者误差在合理范围内，证明了 ABAQUS 仿真模型的可行性和正确性。目前，学者们应用分析软件研究一些参数组合，如滚动长度、复合岩层等对最优刀间距的影响，并发现最优刀间距与围压[29]和贯入度有关，与滚动长度无关[30]。

2.3 刀间距三维确定方法

2.3.1 历史背景

自TBM 产生以来，经历了 20 世纪 50 年代以盘形滚刀压痕试验为基础的第 1 代设计理论，和 20 世纪 70 年代至 80 年代以盘形滚刀线性滚压破碎岩石试验为基础的第 2 代设计理论的发展[31]。20 世纪末，世界上发达国家的地下隧道 (洞)建设基本告一段落，而我国则进入了快速发展阶段，从而使得国际上著名的TBM 制造商一度因我国对 TBM 的进口而复活或兴旺，如 Wirth、Robbins 等，甚至国际上以生产盾构为主的制造商，如 Herrenknecht 等也一度研制 TBM 出口我国。TBM 在我国的应用和发展，使国内学者更全面、客观地认识到了 TBM 盘形滚刀破岩作业的三维属性[32]，促进了 TBM 设计理论[33]和应用技术[34]的发展。

2.3.2 室内试验

TBM 在岩石质隧道 (洞)施工中的优越性能及我国隧道 (洞)工程的发展，引起了我国政府相关部门和相关企业的高度重视，先后建起了“盾构及掘进技术国家重点实验室”(主要试验设备如图 11 所示)和“全断面掘进机国家重点实验室”等国家级实验室，为 TBM 刀间距的三维确定提供了试验手段。目前，研究人员大多先用其他方法确定最优刀间距，再采用盘形滚刀圆形滚压破碎岩石试验去验证所得结论的科学性和准确性[35-36]。文献 [37]通过盘形滚刀圆形滚压破碎岩石试验，发现砂岩、花岗岩形成的复合试样的最优S/P约为 14。

图11 回转切割试验台Fig.11 Circular cutting test bench

2.3.3 软件模拟

刀间距三维确定方法所用的数值模型与刀间距二维确定方法所用的数值模型基本一样，常用ABAQUS 有限元软件建模，同为三维空间模型[38]，如图 12 所示。两者不同之处在于，刀间距的二维确定方法是用盘形滚刀线性滚压破碎岩石的数值模型模拟盘形滚刀破岩过程，而刀间距的三维确定方法是用盘形滚刀圆形滚压破碎岩石的数值模型模拟盘形滚刀破岩过程。文献 [28]使用有限元仿真分析软件ABAQUS 建立了双滚刀回转模型，滚刀为直径 432 mm 的等截面盘形滚刀，破岩对象为 Hwangdeung 花岗岩，岩石本构模型采用 Drucker-Prage，1 号盘形滚刀的轨迹圆半径R=0.836 m，贯入度分别为 4、6、8、10 mm。通过改变 2 号盘形滚刀的轨迹圆半径，模拟刀间距分别为 28、40、48、60、72 和 80 mm。结果发现，破岩比能在刀间距为 60 mm 时为最小值，同时还发现，盘形滚刀圆形滚压破碎岩石的最优刀间距一般介于 60～80 mm[38-40]。

图12 回转切割模型Fig.12 Circular cutting model

3 对比与分析

由上所述可以看出，TBM 刀盘上盘形滚刀刀间距的一维、二维和三维确定方法都是与当时的认知和生产技术水平相适应的，都为 TBM 的技术进步做出了历史性贡献。通过数值模拟发现，针对花岗岩，文献 [16]采用一维确定方法得出最优刀间距约为 70 mm (围压为 1～10 MPa)；文献 [29]采用二维确定方法得出贯入度为 4 mm 时，最优刀间距为 44 mm；文献 [26]采用三维确定方法，得出最优刀间距约为 60 mm。其中文献 [29]与文献 [30]所用刀具、花岗岩岩石参数完全一样，与文献 [18]所用刀具、岩石参数有细微差别，但 3 种方法针对同一种工况得到的最优刀间距并不相同。

目前，研究人员进行盘形滚刀破岩研究的手段已经以盘形滚刀线性滚压破岩和盘形滚刀圆形滚压破岩为主。为分析这 2 种破岩研究的差异，将文献[27](线性破岩模拟仿真)与文献 [28](回转破岩模拟仿真，模拟 1 号盘形滚刀的轨迹圆半径R=0.836 m，通过改变 2 号盘形滚刀的轨迹圆半径，实现刀间距变化)关于 Hwangdeung 花岗岩所得数据进行对比，如表 2 所列。由表 2 可以看出，回转破岩与线性破岩相比，其滚刀所受切向力更大，比能更大。为直观对比2 种模拟方法的差异，以刀间距为横坐标、回转破岩模拟值为真值，给出了盘形滚刀线性滚压相对于圆形滚压破碎 Hwangdeung 花岗岩所产生的平均切向力和破岩比能减小量的百分比，如图 13 所示。从图 13 可以看出，减小量的百分比较大的比能发生在刀间距40～72 mm 之间，而减小量的百分比较大的平均切向力发生在刀间距 40 mm 以下。

此外，文献 [41]在刀间距为 80 mm，破岩刀具和岩石完全一样的情况下进行线性全尺寸切割试验 (贯入度分别为 0.5、1.0、1.5、2.0、2.5、3.0、3.5 mm)和回转全尺寸切割试验 (贯入度分别为 0.5、1.0、1.5、2.0、2.5 mm，回转切割半径分别为 70、150、230、310、390 mm)。通过对比，不仅同样发现回转破岩与线性破岩相比，其滚刀所受切向力更大，比能更大，还发现回转破岩与线性破岩相比，其滚刀所受法向力较小，并且回转破岩过程中滚刀会受到某一个方向的较大侧向力，而线性切割过程中侧向力平均值大体为零。

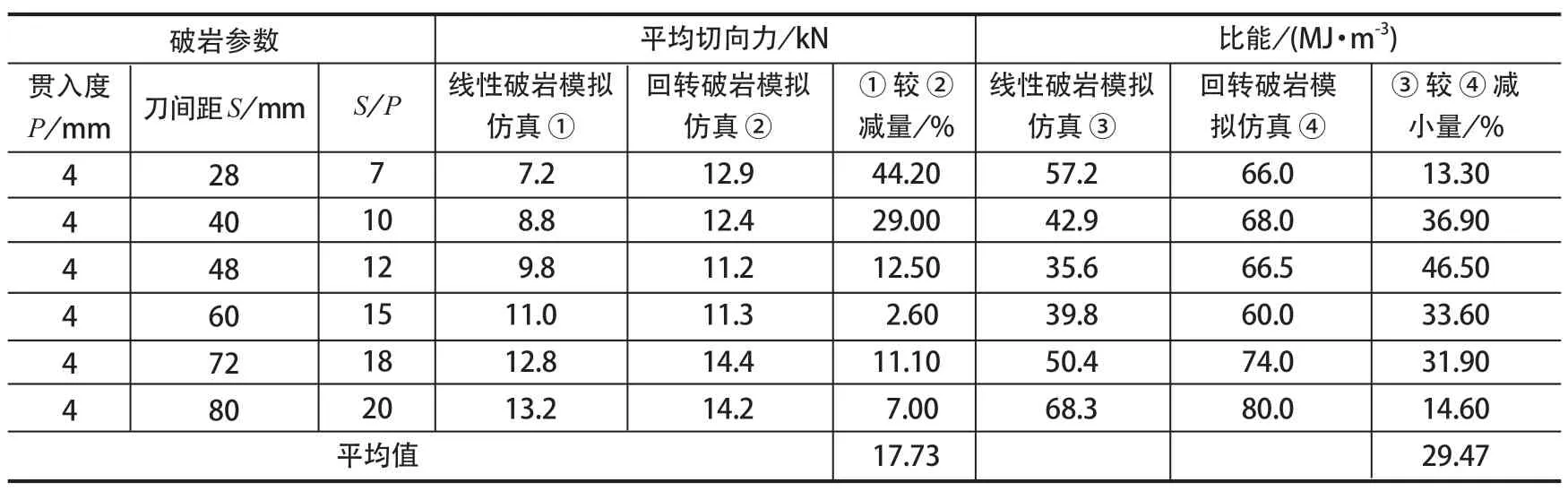
表2 线性破岩模拟仿真与回转破岩模拟仿真数据对比Tab.2 Comparison of linear breaking rock simulation and circular breaking rock simulation in simulation data

图13 盘形滚刀线性比圆形模拟滚压破碎 Hwangdeung 花岗岩的平均切向力和破岩比能的减小百分比Fig.13 Reduction percentage of average tangential force and specific rock-breaking energy consumption of linear rolling and breaking rock with disc cutter compared with circular rolling and breaking rock

4 结论

通过研究盘形滚刀最优刀间距的确定方法发现，目前基本以二维确定方法为主，忽略了盘形滚刀安装半径对最优刀间距的影响。还发现影响最优刀间距的因素确实众多，如岩石种类及其参数、节理、裂隙、不均质程度及其参数等；盘形滚刀安装参数，如安装半径、相位角；切削参数——贯入度等，都对最优刀间距有不同程度的影响。为提高 TBM 利用率、降低TBM 施工成本，在 TBM 发展中心已转入我国的大背景下，客观、科学地确定 TBM 最优刀间距已成为国内科技人员面临的重大挑战。基于这样考虑，得出以下结论：

(1)将 TBM 最优刀间距的确定方法区分为室内试验、工程经验和软件模拟。其中室内试验确定最优刀间距的方法——盘形滚刀压痕、线性切槽 (滚动)和圆形滚压破碎岩石的试验模糊了试验方法与盘形滚刀群实际破岩间的关系。

(2)根据室内试验确定最优刀间距过程中盘形滚刀与岩石的作用关系，理论上可概括为 TBM 刀间距的一维确定方法、二维确定方法和三维确定方法，揭示了 TBM 刀间距的发展、发展趋势和应该深入研究的内容。

(3)目前研究 TBM 最优刀间距所用的盘形滚刀直径大都为 17 英寸，盘形滚刀几何形状及参数对最优刀间距的影响也应深入进行研究。

(4)从对 Hwangdeung 花岗岩采用 Drucker-Prage岩石本构模型的模拟试验发现，盘形滚刀线性滚压破碎岩石的平均切向力和比能都较其圆形滚压破碎岩石的平均切向力和比能为小，分别平均减小 17.73% 和29.47%，揭示了盘形滚刀二维破岩和三维破岩机理的差异，即揭示了安装半径为无穷大盘形滚刀的破岩与有限安装半径条件下盘形滚刀破岩机理的差异。