反映原理作为大基数内在辩护的不可行性

寇亮

1 引言

大基数1一个序数κ 是基数当且仅当|κ|= κ。并非所有的序数都是基数，例如ω+1 不是基数，因为|ω+1|= ω。是集合论中的一个主要研究领域。所谓大基数公理2以可测基数为例，一个基数κ 是可测基数当且仅当存在κ 完全的非主超滤。加入可测基数的大基数公理即：存在可测基数。有时，大基数公理并不是断言某个很大的基数存在，而指它的一致性强度很强，例如“0♯存在”是一个大基数公理，但它断言的是某种非平凡初等嵌入的存在。我们说大基数公理A 比B 强，若在ZFC+A 中能证明ZFC+B 一致。所有大基数公理+ZFC 都能证明ZFC 一致。本文既强调大基数的客观存在性方面，也强调它作为备选公理的一致性一面，因此有时使用大基数一词，有时使用大基数公理一词。，是一些无法在ZFC 中证明的、但和序数的本质紧密相关的命题。

自然的问题是：既然ZFC 无法证明大基数的存在，那么为什么对它的研究会成为集合论的一个重要分支？为什么有集合论学家相信它的一致性，甚至相信它存在？3有些大基数公理断言某个集合存在，而有些大基数公理仅仅是一个强度较强的断言。一致性与存在性也并不总是相同，例如，我们可以相信PA 是一致的，但并不接受自然数作为客观对象存在。

以上问题涉及如何对集合论公理进行辩护（justification）。哥德尔在其《什么是康托尔的连续统问题》（见[5]）一文中最早引入了两种对集合论公理辩护的方式：内在辩护和外在辩护。尽管在讨论集合论公理的文献（可见[4,8,12,13]）中多有对内在辩护和外在辩护二词的提及，但仍有诸多不清晰之处有待研究。例如：什么是内在辩护？目前有什么样的内在辩护？内在辩护能为新公理做何种程度的辩护？

本文之中，笔者将新公理局限在大基数公理。针对上述三个问题，本文将对内在辩护的含义做出一些界定，并基于此考察典型的大基数公理内在辩护——反映原理。面对诸多形式的反映原理，笔者将逐一讨论它们为大基数公理所作内在辩护的成功程度。

2 什么是内在辩护

哥德尔在其《什么是康托尔的连续统问题》一文中认为，如果公理具有数学上的成功性，那么其能够获得外在辩护。其中，“成功性”指：“其成果的丰富性，特别是‘能证实的’成果（的丰富性），即，不使用新公理能证的那些成果，却在新公理的帮助下能异常简洁且容易发现，还能把许多不同的证明压缩成一个”（[5]，第521 页）。

与外在辩护对应的是同时引入的内在辩护。哥德尔认为，有一些公理是内在必要的（intrinsically necessary），我们要引入的新公理可以“仅仅展开了……集合概念的内容”（[5]，第519 页）就得到辩护。更具体一点，哥德尔指出，我们应该寻找那些“断言‘……的集合’运算的更远迭代存在的新公理”（[5]，第519 页），集合就是“那些从整数（或其它良定义的对象）通过迭代应用‘……的集合’运算得到的东西”（[5]，第519 页）。更具体地，哥德尔在未发表的《数学基础的现状》中指出，“假设集合的公理系统（ZF）达到了终点……是错误的。因为，在系统中所有出现的类可以被看作一个新的对象的域，且被用来作为一个新的起点，来创造出更高的类型（type）”（[6]，第47 页）。

P.Koellner 在其《集合论基础——寻找新公理》中总结道，“简单地讲，对新公理的基于集合迭代观念的内在辩护指表明新公理只是展现了集合这个观念的内涵。相反，对集合的外在辩护则着眼于别的特征，诸如丰富成果或与其它公理的结构性关系。”（[10]，第10 页）P.Maddy 在其《为公理辩护》中，将内在辩护总结为自明的、直观的，是“集合这个概念”的一部分，而外在辩护是有效的（effective），丰富的（fruitful）和富有成果的（productive）（[13]，第47 页）。

根据上文提到的哥德尔本人的陈述与Koellner、Maddy 对内在辩护的粗略概括，不难发现，所谓内在辩护，是基于集合这个概念本质的辩护。

然而，什么是集合这个概念的本质？我们如何知道集合这个概念的本质？

讨论集合概念的本质有特别的困难，因为：实在论4这里指数学哲学中的实在论。简单来说，实在论是一种认为抽象的数学对象客观存在的哲学观点。者容易接受有确定不变的集合概念5这不意味着实在论者的集合概念是不变的，而意味着集合概念是客观的，但我们对它的认识是变化的。，因而我们可以讨论它不变的那个本质；而对非实在论者而言，也许根本没有所谓集合概念的本质，因为集合概念并不是一个固定不变的对象。但是，我们可以将讨论的范围限制在广泛接受的范围内，即只讨论ZFC 所确定下来的、我们共同认可的集合。在这种前提下，基于对数学实践的尊重，自然的追求集合概念本质的方法似乎不外乎两种：

1.寻找ZFC 之中的一些定理，论证这些定理向我们传达了我们共同信任的集合概念应该具有的性质。

2.从ZFC 本身中寻找我们共同认可的集合概念应该具有的性质。

以上的第二种方法已经被王浩（见[19]）、C.Parsons（见[14]）和G.Boolos（见[2]）用于讨论集合这个概念的本质，他们从G.Cantor 对于集合概念的理解出发，分别寻找了一些我们共同认可的对集合概念本质的“直观”，并对其进行了一定程度的严格刻画，来说明ZFC 的公理已经满足哥德尔所谓的“……的集合的迭代”。而Koellner 则基于哥德尔相关论述的分析刻画了集合这个概念的特点（见[8]）。

其中值得提到的是王浩、Boolos、Koellner 和Sy D.Friedman 与N.Barton 对集合这个概念的解读。王浩和P.Koellner 明确提到了“V的两个特点”（[19]，第310 页）和“集合这个概念的最关键特征”（[8]，第29 页），他们的总结均基于对ZFC 中V的观察；Boolos 对集合概念的讨论则主要为了表明什么是“……的集合的迭代”（见[2]）；Barton 与Friedman 在2017 年的一篇文章（见[1]）中则考察了极大化原则。

2.1 集合概念的不可穷尽性与不可定义性

王浩在其《大集合》（Large Sets）一文中（[19]，第309-333 页）认为，对一个集合而言，我们只需要保证集合中的元素作为对象存在，而无需保证我们对这些元素有所知。例如，若X是集合，那么P(X)也是集合，尽管我们并不完全清楚每一个X的子集的性质。因此，元素的存在是为了整体（集合）的存在；为了整体存在，这些对象必须存在。而V则没有这个特点：它之中的元素——集合——的存在，反而使得V不能作为集合存在。因此，V是一种比单个的集合更为“高层次”的存在。因此，不能把这样的一个对象作为完成了的对象。这符合Cantor面对V时的态度：“对于那种在由其元素的‘共同存在’组成的这个假设下会产生矛盾的复多而言，不可能接受它们是一个整体，一个‘已经完成之物’。”（[3]，第443 页）

由此可见，王浩与Cantor 同时认为，集合概念不应该是一个像具体集合那样的、已经完成的对象；换言之，作为研究对象而言，集合这个概念是不可穷尽的。这与哥德尔对集合概念的认知是一致的。在哥德尔文集第三卷（[6]）中的《数学基础的一些基本定理和它们的推论》（Some basics theorems on the foundations of mathematics and their implications）一文中指出（[6]，第305 页）：

这些元数学结果都是围绕着一个基本事实展开的，甚至可以说，它们仅仅是其不同侧面，这个事实或可称作数学的不可完全性（incompletability）或不可穷尽性（inexhaustibility）。

即，哥德尔对于数学的理解（亦即是哥德尔对于集合论或者说集合这个概念的理解）是不可完全性和不可穷尽性。

其次，王浩还提到，集合这个概念具有不可定义性（undefinable）。特别地，他指集合概念不能通过任何结构性的性质（structural property）定义（[19]，第318页）。假设A是集合，则其子集也是集合。注意到，这一点与我们是否能用一个性质来刻画这些A中的元素无关，即与可定义性无关。

性质P是结构性质，当：如果仅集合能有性质P，那么所有具有性质P的x组成的复多亦为集合。这个定义的等价于：或者不仅集合能有性质P，或者所有具有性质P的x组成的复多是集合。因此对任意结构性质P有两种情况：

1.一些集合和一些非集合对象都有性质P（析取前件成立）；

2.有性质P的x组成了一个集合，因此有性质P的必须也是集合，故而性质P决定了一个集合（析取后件成立）。

由于V不是集合，因此不可能有结构性质P刻画V：因为第一条表明P还对一些集合也成立；第二条表明P只能刻画集合。因此王浩声称，V是不可使用结构性质定义的。因此能刻画V都不是结构性质，而且我们要非常清楚地意识到这个性质不是结构性质。目前已知的刻画V的非结构性质都几乎不给我们提供信息：例如“……是集合”这个性质不是结构性质，又例如x=x也可以刻画V。在这个意义上，王浩认为集合概念是（使用结构性质）不可定义的。

2.2 集合概念与序数的本质

Boolos（见[2]）和P.Keollner（见[8]）则分别从另外的角度刻画了集合概念的本质。

Boolos 对集合概念的讨论则主要为了表明什么是“……的集合的迭代”，并且基于Cantor 和哥德尔的集合概念论证ZFC 的公理都满足由“……的集合的迭代”推理而来。他刻画了一种阶段理论，它的语言包括变元符号x,y,z···是所有的集合和r,s,t是所有的阶段（[2]，第220-224 页）。所谓阶段，是如下的直观：假设一开始没有任何对象，在第零阶段则将这个空无一物收集起来，即空集；第一阶段则将前面所有阶段形成的所有对象收集起来，即空集和空集的集合；以此类推。语言中还包括两个关系符号E,F，分别为“在……之前”和“在……形成”。Boolos 引入了几条公理，包括断言ω阶段存在的公理：存在一个阶段，不是最早的阶段，也不紧接任何阶段之后。这个阶段理论能推出所有的ZFC 公理，且避免了无穷下降链、避免了断言V是集合。

这一理论是对哥德尔陈述的“……的集合的迭代”的一种精确化。正如Koellner 在其《集合论基础——寻找新公理》中分析的那样，哥德尔的这种方法事实上是从空集出发，顺着有穷类型向上，事实上会得到V0,V1,...,Vn,...，而Vω的构造则完全是将已有的有穷类型作为起点，创造更高的类型Vω，即取前面所有集合的并集。这样的过程无穷无尽进行。这样的方法，实际上将集合概念的无限性转移到了序数的无限性上。

Koellner 在其博士论文中明确指出了集合这个概念的关键特征，即不可定义性。他首先比较了两种哲学立场，一种是潜在主义者（potentialist），一种是实现主义者（actualist）。前者认为V不是形成了一个确定的（determinated）复多，后者认为V是一个完成了的、确定的复多（[8]，第48 页）。他基于对集合观念辩护的实用性6事实上，Koellner 发现不将V 看作完全实现的对象时，反映原理能对大基数做出更强的辩护。而这种方法论自然主义的做法与前面王浩的分析不谋而合。，首先假定V是一个并未完成的对象。因此，与自然数集相比，V满足某种闭包规则。如果无法“自下而上”来刻画V，那么可能其与自然数集类似，是某种闭包。比如，自然数集是对后继运算封闭的最小集合，任意自然数，其后继也是自然数。容易观察到，任意集合的幂集也是集合。尽管V满足在幂集运算下封闭这一闭包规则，但我们发现没有任何闭包规则可以刻画V：因为那样会生成一个新的集合。因此，V拒绝被任何确定的闭包规则所刻画。因此，V是不可定义的。

与王浩的不可定义性相比，Koellner 的不可定义性偏重于强调V不可被“由上而下”，即不可通过对序数进行不断地限制进行定义，而王浩的不可定义性则偏重于强调V不可被描述地定义。

2.3 极大化原则

另一种基于哥德尔“……的集合的迭代”的观察是极大化原则。例如，Barton与Friedman 在2017 年的一篇文章（见[1]）中指出，基于集合的迭代：

集合论语句的真值由宇宙的“宽度”和“高度”决定7“高度”指什么样的序数存在，使得其能成为Vα 的下标α，“宽度”指的是Vα 的哪些子集在Vα+1 之中。见[1]。，因此，集合概念的一个特征是极大性。从不同的哲学观点出发，对极大性的理解也各不相同。例如，有的人会认为集合宇宙应当包含非可构成的集合以满足极大性，因此根据极大性；有些人会认为序数应该在某个运算下封闭以达到极大性（不难指出不可达基数即符合这种极大性）。尽管集合论学家对极大化原则有不同侧面的理解，但他们对这一策略整体上持正面态度。王浩也曾评论：“我们相信所有序数的类是非常‘长’的，并且每一个无穷集合的子集是非常“厚”的。因此，任意达到这个效果的公理都满足了我们直观。”（[19]，第315 页）

2.4 集合概念的本质

基于上述的分析，我们可以将模糊的内在辩护这一概念进行具体化。内在辩护是根据集合概念的本质进行的辩护，而集合概念的本质包含以下几个方面：

1.可以从ZFC 的定理出发，刻画集合概念的特质并以此对公理进行辩护；

2.集合概念是非完成的、不可穷尽的；

3.集合这个概念要满足极大化原则；

4.集合概念是不可定义的，包括不可通过限制进行定义和通过描述进行定义；

5.集合这个概念的本质主要体现在序数的本质上。

由此，我们可以依据上述特性，论证反映原理可以是大基数公理的一种内在辩护。

3 反映原理及其限度

反映原理是基于ZFC 中的反映定理提出的若干条假想公理。反映定理说，对任意有穷的公式集而言，存在一个整个宇宙的“初等子模型”。即，使用有穷多语句描述的集合宇宙的性质，都能在集合宇宙的一部分中找到一个对应，这个更小的宇宙足以反映集合的宇宙所拥有的那些性质。

定理1(反映定理).给定任意公式φ1,...,φn，（[11]，第136 页）

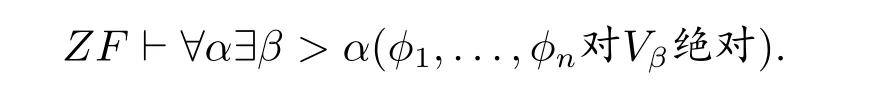
反映原理被普遍接受为一种有力的内在辩护方式。因为，反映定理暗示我们，也许整个集合宇宙V的任意性质都会反映到其一个片段Vα之中。这样，ON的性质也会反映到Vα中。特别地，ON的无限性特征也会被分别反映到不同的Vα之中。正如我们在哥德尔方法一节中所讲，哥德尔的方法实际上是将数学的无限性转化到序数类ON的无限性上，因此，不同的反映原理实际上表达了我们对集合这个概念能认识到何种不同的程度。而对不同反映原理的辩护能到什么程度，我们对ON无限性的刻画就能到什么程度，对大基数的辩护亦相应能到不同程度。

我们期待的反映原理是如下的形式：

即，任意的集合宇宙V中的性质φ，都会在V的一个片段Vα中成立。

可以将RP1 具体化为RP2 中的多种形式。我们能在ZFC 中证明的反映定理只是RP1 的一阶形式，即我们限定φ是一个一阶公式，有：

我们将φ为更高阶的公式时的反映原理分别称为RP2.1，RP2.2，……这样形式的反映原理能被广为接受，是因为反映定理是ZFC 的一个定理，并且，基于迭代方法，我们知道了集合宇宙的无限性体现在序数类的无限性上，集合宇宙的每个性质体现为某个序数κ的性质，即Vκ的性质。

Reinhardt 在他的文章中（见[15-17]），基于一种“合理候选人”理论，提出了加入二阶参数的反映原理：(Vα0,X)≺(Vα1,j(X))8我们这里同样使用≺符号表示二阶形式的初等嵌入。将语言扩张到含二阶对象，则除一般初等嵌入的定义外，带二阶参数的初等嵌入还要求保持二阶对象。在下一节还将会有说明。。这种形式的反映原理是一种不同层间的反射，能证明存在可扩张基数。

P.Welch 则于其2012 年的文章中（见[20]）提出了一种片段与V之间的、全局的（Global）的反映原理。令V下所有类为C。Welch 的反映原理断言，(V,∈,C)会被反映到(Vκ,∈,Vκ+1)之中。准确地讲：

存在一个非平凡的初等嵌入j和一个序数κ满足crt(j)=κ，使得：

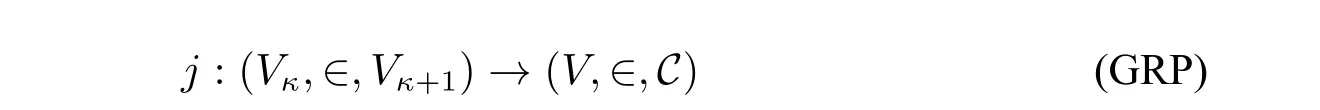
上面我粗略介绍了反映原理的几种形式，下面我将详细介绍几种反映原理的强度和面临的困难。

3.1 RP2 的极限

Koellner 在他的博士论文之中考察了RP2 的二阶形式和高阶形式能达到的极限。二阶形式的反映原理允许类作为参数和量词限制的对象：

定义1.令Lα,β是有≤α阶量词和≤β阶参数的集合论语言。我们用x,y,z...表示一阶对象，用X(α),Y(β),Z(β)表示β阶对象，用ON表示全体序数的类。（[8]，第30 页）

首先我们考虑二阶对象的相对化。类似一阶对象的相对化，我们令二阶对象A(2)对Vα的相对化A(2)α=A(2)∩Vα，即Vα看A(2)时会省略那些不在其世界中的部分。对公式相对化到Vα，则将二阶量词约束的对象限制在Vα-1，即这些对象属于Vα。

二阶形式的RP2 能为较小的二阶大基数做辩护。事实上这些二阶形式的大基数无非在重复我们对于集合宇宙不可定义的直观。L2,2中，ON本身是不可达的，且ON下有任意大的不可达基数：因为，（在V中）ON是不可达基数的一个极限，根据二阶反映原理存在某一层Vα(2)中ON也是不可达基数的一个极限，且下面除ON外还有真类β(2)多个不可达基数。类似地，ON也是马洛的：因为令C是任意ON中的club9本文用club 指代闭无界集（closed unbounded set）。，可知（在V中）C在不可达的ON中无界，因此在某一层Vα(2)中，C ∩α(2)在不可达的ON ∩α(2)中无界，且是一个club。由于C是ON中的club，因此C中小于ON的极限点都在C中，因此不可达的ON ∩α(2)也在C中，因此C与这些ON下的不可达基数全体总是相交，故在ON下的不可达基数构成了平稳集。类似地，还可以证明ON是弱紧致的、不可描述的10需要注意的一个细节是，Koellner 的证明中所使用的相关大基数的定义与通常定义不尽相同。例如，对一集公式Γ，他定义κ 是Γ-不可描述的当且仅当Vκ |=Γ-反映原理，这里的Γ 反映原理以Levy 层谱为标准，例如反映原理。具体可见[8]。。可得到如下事实：

定理2.假设ZF+L2,2-反映原理，则存在二阶的不可达基数、马洛基数、弱紧基数、不可描述基数。（[8]，第45 页）

而含高阶参数的高阶形式反映原理则不适用于为大基数做辩护，因为它们蕴涵矛盾。以三阶形式为例，它是不一致的。出现矛盾的地方则是三阶对象的相对化。我们如何相对化三阶对象？或者说，Vα将如何看这些三阶对象？一个自然的考虑是三阶对象包含的是二阶对象，因此相对化三阶对象只需相对化二阶对象，再取这些二阶对象的类。即Y(3)α={X(2)α|X(2)∈Y(3)}。这种相对化方法和一阶、二阶对象的相对化是一致的。

考虑三阶类A(3)，它包含所有具有如下性质的二阶类：包含有界序数的所有前段。如果将所有包含小于α序数的二阶类记为[0...α)11它们对Vα 而言都是二阶对象。，则A(3)={[0...α]|α ∈ON}。

此时会出现违背三阶反映原理的结果：令Φ(X)为X的每一元素都有界。则显然，Φ(A(3))每个元素有界，它们的高度都在ON之下，即Φ(A(3))成立。那么根据三阶反映原理，存在某个β使得Φ(A(3))的任意元素在Vβ中有界。但，我们将A(3)相对化到Vβ，现在考虑那些在β之上的A(3)中的元素（因为Vβ中的元素秩都小于β），把它们全部切掉。我们会发现上部被切掉的部分在β中无界。因此Φ(A(3)β)在Vβ中不成立，矛盾。因此：

定理3.三阶反映原理不一致。（[8]，第50 页）

因此，RP2 无法很好地为大基数做辩护。

3.2 Reinhardt 的反映原理及其问题

W.Reinhardt 所使用的集合论以及他对集合概念的理解均来源于Ackermann（见[15]）。Ackermann 声称，对集合的良好定义不能包含“……的集合在V中”这样的陈述，即集合x的定义不能使用形如y ∈V的表述。同时，他允许使用V并将其看作已经完成的对象，因此我们还可以谈论或者想象{V}这样的对象。这种观念来源于Cantor，他使用VΩ这样的记号，并声称我们可以想象VΩ之外的“似集合的对象”。

假设我们有V的多个候选解释Vα0,Vα1,Vα2....，则根据Reinhardt 的结论，以前两个解释为例，对任意语句σ，都有：Vα0|=σ当且仅当Vα1|=σ。这意味着它们初等等价。对有参数的公式φ(x)，则有：

注意，这意味着Vα0≺Vα1，并且这个初等嵌入j0是在α0之下是平凡的。这就是Reinhardt 的一阶形式反映原理，它是一种固定片段之间的相互反映。

此时，我们再将语言中加入二阶参数。先看一种情况：假设X ⊆Vα0是对Vα0而言的二阶对象，则Reinhardt 要求，(Vα0,X)也应该反射到某一层，因此初等嵌入j也会重新解释X，使得j(X)是Vα1之中的类，并且(Vα0,X)≺(Vα1,j(X))。此时，则存在初等嵌入j使得：

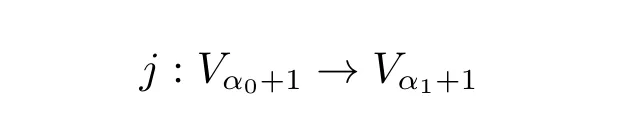
注意到，在α0之下的那些序数β，显然由于见证Vα0≺Vα1的j0在α0下是平凡的，因此j(β)=β。反之，由于j(X)显然是不同于X的一个解释，必有j(α0)≠α0，故而crt(j)=α0。这意味着α0是1-可扩张基数。

更一般地，由于Reinhardt 允许VON,ON作为对象出现，那么对于VON的二阶对象ON而言，(VON,ON)也会相应地有一个(Vj(ON),j(ON))使得crt(j)=ON。这意味着VON+1≺Vj(ON)+1。对任意大于ON的λ亦如此。这意味着ON是可扩张的，因此根据反映原理，存在可扩张基数。继而存在超紧基数。

但是Maddy 和Koellner 同时指出了Reinhardt 反映原理的不可靠之处。

第一个问题是，一系列的解释Vα是没有尽头的：

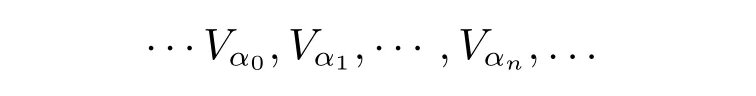
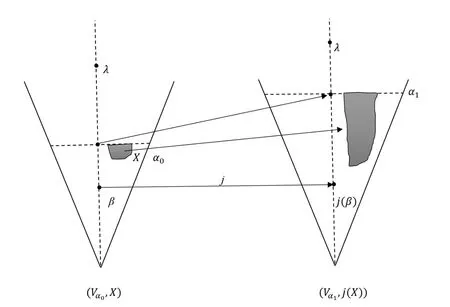
图1 :带二阶参数的Reinhardt 反映原理

Reinhardt 的一个重要前提是，这些V的解释之间初等嵌入总是存在，这才使得我们能够得到后面的非平凡初等嵌入。但Kunen 告诉我们12可见集合论教材[7]，第323 页。，V到V之间不存在非平凡的初等嵌入，并且L到L之间存在非平凡初等嵌入需要0♯这样的大基数来保证。因此，很难保证假设总是存在非平凡的初等嵌入不会导致矛盾。

并且，由于这些Vα全部都是V的前段，Reinhardt 很难解释为什么不选用最高的某一层作为V的最有力的解释，而要将所有的Vα视为平行的对V的解释。例如，比较Vω和Vn，显然Vω有更强的闭包性质，因为它对自然数的后继运算封闭。

即便忽略上述问题，仍然有其它问题。其一则是Maddy 和Koellner 都提及的追踪问题（Tracking Problem）（见[9,12]）。以上文的Vα0和Vα1为例，我们不知道这个j是什么样的初等嵌入，当问j(X)是一个什么样对象的时候，则难以追踪X在Vα1中的性质，只能非常模糊地讲是某个对象j(X)。对可定义的子集X ⊆Vα0这一点容易办到，可以通过定义X的参数和公式追踪j(X)，但对于j(X)而言，很难知晓这是个什么样的对象，因为这个初等嵌入j对我们而言是模糊的。而这个Vα的序列无穷进行，将有数量庞大的模糊的对象出现。这是不可接受的。

再次，即便允许V、ON这样的对象是完成的对象，可以使用，但让人难以理解的是“ON+1”、“VON之外”这样的概念。毕竟，除了它们没有良好的定义之外，我们还很难想象V之外的所谓“类似集合的对象”是什么样。

最后，Reinhardt 的反映原理是固定层数的反映原理，甚至某种意义上讲，他的反映原理就是可扩张基数本身的定义。如果他的反映原理可以被当作反映原理合理地使用，那为什么我们不可以直接使用可测基数、超紧基数的定义作为反映原理？因此这种“反映原理”对大基数的辩护显然是不成立的。

3.3 Welch 的GRP 及其问题

尽管RP2 和它的修改版本、Reinhardt 带有哲学背景的反映原理都不能很好地为大基数的存在性或者一致性做出辩护，但是，仍然有集合论学家和哲学家尝试找出超出V=L的反映原理。RP2 看起来太弱：它试图超出0♯，却无法达到ω-Erdös 之上；而Reinhardt 的反映原理看起来太强：它能证明存在可扩张基数，但却同时也无法完全避免出现V到V的非平凡初等嵌入。那么，是否可以寻找一种反映原理，证明存在Woodin 基数的真类？

前文中的反映原理尝试了在语言中加入高阶参数、允许高阶量词，也尝试了在不同层数之间使用高阶参数进行反射。而Welch 则引入了某些特定高阶对象的类进行反射（见[20]）。V的“部分”既包括了一些集合，也包括了一些类，例如序数类ON。我们令所有V的“部分”为C。则GRP 断言，任意(V,∈,C)的性质都会在某个(Vκ,∈,D)中已经成立。其中，D是Vκ的某些“部分”，即其中有一阶对象：Vκ中的集合，也有二阶对象：秩为κ的集合。因此，D ⊆Vκ+1。

定义2.定义GRP 如下：存在非平凡初等嵌入j满足crt(j)=κ，使得：（[21]，第9 页）

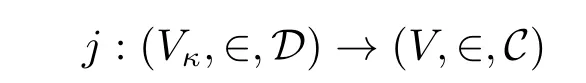
可知此反映原理的强度与D的宽度相关。若D极端“窄”，则j表达的东西极少。例如D=∅时，则是前面讨论过的RP2。如果D取到合适的宽度，则可以获得足够强的大基数。首先，它可以达到我们的最低目标。

定理4.假设P(κ)L ⊆D ⊆Vκ+1。若存在j使得crt(j)=κ满足j:(Vκ,∈,D)→(V,∈,C)，那么0♯存在。

证明.由于P(κ)L ⊆D ⊆Vκ+1，可知κL ∈D，且可知j(κ)=ON ∈V。我们定义κ上的L-滤（即U ⊆P(κ)∩L）如下：

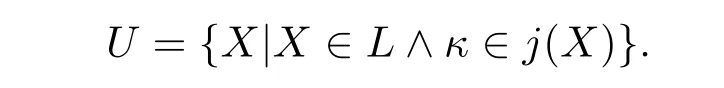
容易验证这是一个κ完全的非主超滤。令Ult(L,U)为L在U下生成的超幂模型。令j0见证L是Ult(L,U)初等子模型的初等嵌入。由莫斯托夫斯基坍塌和哥德尔凝聚引理，可知存在π见证Ult(L,U)与L同构，因此j′=j0◦π是L到L的非平凡初等嵌入。因此0♯存在。

我们引入Shelah 基数和Woodin 基数的几种等价刻画。

定义3.κ是Shelah 基数当且仅当对任意f:κ →κ，存在传递的M使得j:V →M满足

1.crt(j)=κ；

2.Vj(f)(κ)⊆M。（[18]，第3390 页）

Woodin 基数有如下的等价定义（[7]，第384 页）：

1.κ是Woodin 基数；

2.对任意f:κ →κ，存在α ＜κ使得存在传递的M，j:V →M满足：

(a)crt(j)=α；

(b)f[α]⊆α；

(c)Vj(f)(α)⊆M。

3.对任意f:κ →κ，存在α ＜κ使得：

(a)f[α]⊆α；

(b)存在扩张（extender）E ∈Vκ且jE(f)(α)=f(α)，Vf(α)⊆UltE。

可证明，任意的Shelah 基数都是Woodin 基数。现在，考虑D=Vκ+1这种极端情况。可以利用D=Vκ+1时的GRP 证明存在Shelah 基数。

定理5.假设GRP且D=Vκ+1，那么κ是Shelah基数。（[21]，第10 页）

因此可以有如下证明存在Woodin 基数的真类：

因此，我们有：

定理6.GRP可以证明V中存在Woodin基数的真类。（[21]，第10 页）

GRP 看似是一种强大的反映原理，或者说，它似乎是前面各类反映原理的一个推广。Welch 同样引入了二阶参数来为大基数做辩护，但他的二阶参数并不是允许在语言中使用高阶量词和高阶对象，他似乎明确地指出了C是哪些二阶对象，即V的所有“子集”。那么，GRP 是本文语境讨论下的可用于内在辩护的反映原理吗？

首先需要考察GRP 是否是本文语境中讨论的反映原理。我们先看哥德尔心中的反映原理是什么样的：

“所有确立集合论公理的原则都应该能归约到阿克曼的原则：绝对（无穷）是不可知（unknowable）的。这一原则的强度随着我们获得越来越强的集合论系统而增强。其他的原则都是（这一原则）派生的原则。因此，核心的原则是反映原则，它可能将随者我们经验的增加被更好地理解。同时，它还帮助我们分离出更多的具体原则，这些原则或者给我们更多信息，或者我们尚未从现在理解的反映原理中推理出来。”（[22]，第七章）

GRP 类似Reinhardt 所介绍的Ackermann 反映原理（见[15]）。这是一种“语法”的反映原理，即它是与具体的每条公式F(y,x1,...,xn)和具体的集合y,x1,...,xn相关。相反，GRP 的形式不是如此，甚至存在(Vκ,∈,Vκ+1)是(V,∈,C)的子结构，这件事是无法在一般的一阶逻辑中表达的，因此在一般的意义下，它当然不是可以通过(V,∈,C)定义的。如果说一般的反映原理是试图刻画“我们的语言无法固定集合宇宙”，那么GRP 相比之下则是断言存在一个D和j，以至于有一个刻画(V,∈,C)的子结构。从这个意义上来看，显然GRP 不是我们所认可的具有内在辩护合法性的反映原理。

其次，GRP 显然总是依赖一个不可定义的j和D来进行论证。它不仅不是一阶的，更是不可定义的对象。考虑如下命题，假设V=HOD，令X={A:A在V中不使用参数可定义}。那么我们有X是HOD 的初等子模型：假设对任意φ(x,和任意∈X，若HOD|=∃xφ(x,，则存在一个集合a使得HOD|=φ(a,。由选择公理，令a0是最小的见证这一点的a，可知a0可定义且HOD|=φ(a0,。由于X是HOD 的初等子模型，在V=HOD 下，V中的元素都应该是可定义的。V=HOD 是一个有诸多证据的命题。由此，使用不可定义的对象对V中大基数进行辩护的论证都不可靠。

最后，尽管GRP 体现了“集合概念的不可穷尽”特性，但蕴含集合概念不可穷尽特性的命题很多，这些命题并不都能看成是对大基数的内在辩护。例如，对可测基数，我们令“原则U”定义如下：存在可测基数的平稳类13S 是一个平稳集当且仅当其与任意闭无界集相交非空。。则可知14原则U 和下列结果来自笔者与H.Woodin 教授的讨论。：

定理7(ZFC).下列等价：

1.原则U；

2.任意可定义的序数闭无界类C，存在κ ∈C是可测基数；

3.对任意n，存在无界多κ使得Vκ ≺Σn V且κ是可测基数。

证明.我们证明2 与3 等价。

2 推3：对任意序数闭无界类，都可以取κ为可测基数，此时存在传递模型M使得M ≺V且crt(j)=κ。易知，因此对任意Σn语句，有Vκ ≺Σn M ≺V。

3 推2：由于“存在闭无界类C”是Σn+1的，因此若κ满足Vκ ≺Σn V，则Vκ也满足“存在闭无界类C”，因此在κ下有无界多C中的点。而由于C是一个闭无界类，故κ ∈C。

因此，若令定理7的第三条为RP*，那么对原则U 的断言实际上等价于某种形式的反映原理RP*。并且，我们有一些ZFC 的定理支持我们接受RP*：

定理8.1.若κ是不可达的，那么Vκ ≺Σ1V。

2.若κ是超紧基数，那么Vκ ≺Σ2V。

3.若κ是可扩张基数，那么Vκ ≺Σ3V。（[7]，第384-385 页）

因此，按照Welch 的做法，我们完全可以认为RP*是一种反映原理。若假设RP*成立，则从ZFC+RP* 可得原则U，即可获得可测基数的平稳类。并且，这种反映原理强度强于可测基数，其强度在o(κ)=1 和o(κ)=2 之间15o(κ)指κ 的Mitchell 秩。。对许多大基数公理，我们都能构造类似原则U 的命题。这些命题从表面上看刻画了V的不可定义性，并且可以从一些定理得到形式上的支持；可以证明，这些命题能够使我们获得比可测基数更强的大基数。但是，这种反映原理并不给我们某些特定大基数存在的证据。因为这些反映原理事实上等价于断言存在某些大基数的平稳类。换言之，对于断言这些大基数存在，我们需要一个解释（explanation），尤其是需要集合论内部的一个解释。如果这个解释实际上等价于断言大基数的存在，那么显然它不是对大基数存在的合法解释。

在以上两种意义上，笔者认为GRP 不能作为大基数的合理内在辩护。

4 总结

基于哥德尔所提出内在辩护的涵义，不难发现内在辩护就是基于集合概念本质的辩护。然而什么是集合概念的本质？在考察了王浩等人的工作后，笔者简单总结了集合概念的几个特点，即不可完全性、不可定义性、需要满足极大化原则和与序数概念紧密相关。如果我们这样界定集合概念的本质，那么反映原理的确是一种内在辩护。利用反映原理的几个变种：RP2、Reinhardt 的反映原理和Welch的GRP，我们的确可以获得不同强度的大基数，甚至可以获得Woodin 基数的真类。但是正如前文所述，笔者认为这些反映原理或者强度不够，或者存在哲学上的困难。因此目前我们无法使用反映原理对大基数进行内在辩护。

那么，这是否意味着对大基数的内在辩护是失败的？笔者认为，反映原理对大基数公理辩护的失败，很可能源自于我们对于“集合概念的本质”的界定是过于简单的16例如，从我们对“集合概念的本质”的界定来看，甚至很难说明为什么反映原理的确比大基数公理本身更加“内在”。。不仅如此，笔者认为，尽管目前我们对集合概念在数学上有了一些理解，但对这些数学结果的利用是远远不够的17我们在前文对“集合概念的本质”的界定几乎没有使用到任何当代集合论发展的成果，例如力迫。，这是我们对“集合概念的本质”缺乏认知的重要原因。因此，本文的结果并不意味着对大基数的内在辩护是不可能的，而仅仅意味着反映原理无法很好地为大基数公理进行内在辩护。同时，这也意味着对集合概念的本质的探索将是一个有广阔前景的问题。