模态版中文屋论证研究——兼对某种模态论证模式的探究

冯书怡

“中文屋论证”（the Chinese Room Argument）是上世纪八十年代著名哲学家塞尔（J.Searle）提出的思想实验，用以反击强人工智能的观点。1为了简化行文，下文在大多数情况下将“中文屋论证”简称为“CRA”。在随后的几十年里，哲学家们对CRA 的讨论汗牛充栋。基本上，学界一致认为CRA 是错的。2这也是笔者的立场。但是至于它为何是错的，学界众说纷纭。（[3]，第163 页）这是因为，CRA 虽然名义上是一个“论证（argument）”，但实际上仅仅是一个思想实验。如果要判断它是否以及为何（不）成立，我们首先必须把它重构成一个论证的形式。然后我们才能检验这个论证形式上是不是有效的，以及其各个前提是不是为真。如果我们采用不同的方式对其加以重构，那么我们对CRA 错在哪里的诊断或许就不同。3导致纷争的另外一点是，有些重构方式也许牺牲掉了中文屋思想实验中的重要直觉。如果我们对于中文屋思想实验的批评是由于我们树立了一个很弱的靶子，即一个稻草人，那么这种批评无疑是没有说服力的。所以任何一个值得被认真对待的重构版本必须在最大程度上保留中文屋思想实验的原始直觉，至少要保留它的核心直觉。许多学者都试图对CRA 提供了重构论证，从不同的角度论证了CRA 的错误。但正如沙非（M.Shaffer）所说，鲜有学者从逻辑层面挑战CRA。4关于CRA 不同的重构形式，参见[3,5]。

沙非（[12]）提供了一个模态版本的重构，试图从逻辑的角度论证CRA 的错误之处。沙非认为该模态论证存在逻辑漏洞，因而是不可靠的。努特（D.Nute）随即对沙非的批评提出了反驳。（[8]）努特认为，其一，沙非的批评源自其对该模态论证某个关键前提的论域的误读；其二，该模态论证因此并不存在沙非所说的逻辑漏洞。笔者将论证，努特对沙非的第一点反驳是正确的；但第二点反驳缺乏证据。笔者将进一步论证，沙非对该模态论证的批评也缺乏证据。所以，笔者认为：仅凭沙非和努特的论证，我们并不能证明该模态论证是不是具有逻辑漏洞，从而无法以其为媒介证明CRA 本身是不是具有逻辑漏洞。5请读者注意，此处笔者并不是认为CRA 本身没有问题。笔者仅仅是指出，我们无法凭借沙非构造的这个模态论证为中介来证明CRA 本身的错误之处。更进一步，笔者从沙非和努特的论辩中总结出模态讨论中常见的论辩模式。笔者指出该模式涉及的模态前提难以得到辩护，因此这种模态论辩模式缺乏实用性。

1 强人工智能和中文屋论证

塞尔提出CRA，旨在反驳强人工智能。6根据塞尔的观点，强人工智能指的是：计算机本身等同于心灵。与强人工智能相对的是弱人工智能，其主要观点是：计算机是用以模拟心灵的工具。参见[13]。后者的核心观点是：“计算机不仅仅是研究心灵的工具。一旦给定了正确的程序，计算机就可以说是具有理解能力并且拥有其它的心灵状态。在这个意义上，被恰当编程的计算机实际就是心灵。”（[13]，第417 页）如果强人工智能的观点是正确的，那么一台被恰当编程的计算机就能够像我们母语者一样理解自然语言。

但问题是，计算机对于自然语言的处理都是通过识别语法（syntax）实现的，也就是说，计算机的输入和输出都是通过识别字符串的形状来实现的。然而，作为心灵的拥有者，我们人类母语者对于自然语言的理解要求我们掌握字符串的语义（semantics）。如果对于语法的操作并不能充分保证对语义的理解，那么计算机就不能被看作是心灵。在塞尔看来，语法确实不是产生语义的充分条件。因此，塞尔认为计算机不是心灵。塞尔对于强人工智能的反驳思路可以被整理为以下论证：

P1:计算机程序的运行是通过语法实现的。

P2:心灵对于语言的理解是通过语义实现的。

P3:语法不能独自成为语义的充分条件。7在塞尔的原文里，塞尔的第三个前提是一个合取式：“语法既不能独自成为语义的充分条件也不能独自成为语义的构成性条件”。（参见[14]，第27 页）。为了简化论证，也为了对应后文将要介绍的沙非的论证，本文只讨论这个合取式的一支：语法不能独自成为语义的充分条件。

结论：计算机程序不是心灵的充分条件。

由此可见，塞尔的观点和强人工智能的观点针锋相对。后者认为计算机程序等同于心灵。这就意味着，后者认为计算机程序就是心灵的充分条件。而前者持相反观点。在塞尔上述反强人工智能的论证中，P1和P2都是毋庸置疑的。因此，分歧的关键在于P3，也就是语法是否能独自成为语义的充分条件。塞尔认为答案是否定的。为了给P3提供辩护，塞尔提出了CRA。

塞尔让我们想象如下场景：被试被锁在一个房间里。他只懂英文，但从未学过中文。在这个房间里，被试有：(1)一堆海量的印有中文字符串的纸条；(2)一本用英语书写的规则书。这本规则书书写了任何两个中文纸条，如Cj和Ci的对应关系。比如，这本规则书会说明纸条“人固有一死吗？”和纸条“是”是相对应的。测试者和被试通过传递纸条进行提问和回答。比如，测试者向屋内传递一张写着“人固有一死吗？”的纸条。被试通过查找英文规则书，发现应将写着“是”的纸条递出去。这本英文规则书给出了所有中文纸条间的对应规则，也就是说，对于测试者递进房间的任何一个中文纸条，被试都能通过阅读英文规则书知道哪张纸条才是合适的回答。那么，通过反复地递进和递出纸条，测试者并不能发现被试实际上不懂中文。然而，被试似乎确实不在我们母语者理解中文的意义上懂中文：他并不知道“人固有一死吗？”意味着“Are all human beings mortal？”，他也不知道“是”意味着“yes”。在和测试者进行中文交流的过程中，被试完全是通过识别汉字的形状而不是通过识别汉字的意思来进行的。

CRA 给反强人工智能论证中的P3，即，语法不能独自成为语义的充分条件，提供了强烈的直觉上的支持。那么，CRA 是否真的能为P3提供论证上的支持呢？这取决于CRA 是否是一个可靠的（sound）论证。然而，CRA 虽然名为“论证”，实际上只是一个思想实验。CRA 的可靠性依赖于它如何被重构成一个论证的形式和重构版本的可靠性。在下文中，笔者将以沙非提供的模态版的重构论证为讨论对象，并以此为基础来探讨CRA 的可靠性问题以及其引发的关于模态讨论中关于模态辩护的问题。

2 关于CRA 的模态论证

2.1 沙非的模态论证

沙非（[12]）为CRA 提供了一个模态版本的重构：

1 屋中人不懂中文。

2 屋中人懂英文。

3 屋中人有一堆印有中文的纸条{Ci,Cj,…,Cn}。

4 屋中人有一本用英文书写的规则书，书上说明了任何一对中文纸条〈Ci,Cj〉的对应关系。

5 对“如果给定Cj，那么输出Ci”的操作指导也是用英文写的。

6 屋中人对于中文纸条的操作和一个中文母语者在行为上是无法区分的。

7 如果前提1-6 的合取是可能的，那么语法不是语义的充分条件。8从此处开始，如无额外的限定，本文所有的“可能”以及“可能性”的出现都指的是形而上学可能性。当然，为了与其它可能性，如逻辑可能性相区分，笔者也会用“形而上学可能性”来指称形而上学可能性。

8 前提1-6 的合取是可能的。结论：语法不是语义的充分条件。9沙非原文写的是“语法不是心灵内容（mental content）的充分条件。”（参见[12]，第231 页）为了使得他的论证和塞尔的原始文本保持一致，以避免不必要的误解，本文将沙非论证中的“心灵内容”修改为“语义”。

2.2 沙非对塞尔的反驳

在沙非提供的模态论证中，前提1-6 都是原原本本的对CRA 思想实验场景的描述，因此它们为真不存在争议。那么，这个模态论证的可靠性（soundness）就完全取决于前提7 是否为真。沙非认为，如果塞尔认为前提7 为真，那么他不得不接受下述论题：

论题1：不存在任何可能世界，在其中前提1—6 为真，且在其中屋中人懂中文。10沙非原文写的是“不存在任何可能世界，在其中前提1-6 为真，且屋中人在以下意义上懂中文：屋中人有跟中文母语者一样的大脑状态。”为了简化行文，本文作了缩略处理。（参见[12]，第234 页）并请读者注意，后文所谈论的“是否懂中文”也是在“是否有跟中文母语者有一样的大脑状态”这个意义上谈论的。

沙非认为论题1 不成立，因而前提7 为假。为了反驳论题1，沙非设想了一个可能世界w1。在w1中，前提1-6 都为真，而且w1和我们的现实世界其它方面都是相同的。但唯一与现实世界不同的是，w1上有一个突现的属性（emergent property）：足够丰富的语法体系恰好是语义的充分条件。所以在w1上，屋中人是懂中文的。既然存在一个可能世界，在其中前提1-6 为真且屋中人懂中文，那么论题1 就被驳倒了，从而前提7 也被驳倒了。11在此我们暂时搁置可设想性和可能性的关系问题，并假设沙非是对的：一个可设想的世界就是一个真正的形而上学的可能世界。概括地说：沙非对于模态版CRA 的反驳分为两步：一、重新解读前提7；二、通过设想一个可能世界来反驳前提7。

2.3 努特对沙非的反驳

努特在[8]中对沙非的批评作出了反驳。其反驳的核心有两点：首先，沙非对前提7 的解读过强，因而是错误的。然而，在没有追加任何其它论证的情况下，努特直接断言：沙非对于前提7 的反驳也是错误的，因而模态版CRA 不具有沙非所指出的逻辑漏洞。

努特认为：“语法不是语义的充分条件”意思是说“语义并不总能（not always）从语法中产生”。然而，沙非却将这个命题理解为“语义从不（never）从语法中产生”。（[8]，第432 页）如果用可能世界语义学的工具来解释，努特认为前提7 迫使塞尔接受的是一个比论题1 弱得多的承诺，即论题2：

论题2：存在一个可能世界，在其中前提1-6 为真，且在其中屋中人不懂中文。

沙非和努特所讨论的可能世界都有一个共同的特点，即，在其中前提1-6 为真。因此我们不妨将论域缩小至所有在其中前提1-6 为真的可能世界集，以便更直观地看出沙非和努特对前提7 解读的差异。12在其中前提1-6 为真的可能世界集决不会是空集，这一点由模态论证的前提8 来保证。沙非认为前提7 蕴涵的是：

对于任何可能世界，在其中屋中人不懂中文。而努特认为前提7 蕴涵的是：存在一个可能世界，在其中屋中人不懂中文。13当我们谈论“屋中人是否懂中文”的时候，我们实际上谈论的是在塞尔所设想的可能世界中是否存在语义。

不难看出，努特对于前提7 的解读使用的是存在量词，只关乎一个可能世界。而沙非使用的是全称量词，关乎所有可能世界。后者是一个非常强的宣称。如果要击败后者，只需提供一个很弱的证据（即，关乎一个可能世界的描述）即可。在沙非的文章里，他就诉诸于“语法是语义的充分条件”之可能性这个证据来击倒前者。然而，在努特看来，沙非对于前提7 的解读是错误的。更进一步，他认为沙非提供的模态论证并不存在沙非所说的逻辑漏洞。

3 对双方的回应

接下来，我们将分两部分来探讨努特对沙非的批判是否正确：一、沙非对于前提7 的解读是否是错误的；二、该模态论证是否不存在沙非所说的逻辑漏洞。

3.1 关于前提7 的解读

首先，我们必须弄清当我们说“p是q的充分条件”时，我们到底在说什么。“p是q的充分条件”表达的并不是一个实质蕴涵（material conditional）：

如果p，那么q。

而是一个严格蕴涵（strict conditional）：

必然地，如果p，那么q。

如果利用可能世界语义学这个语言工具来进行“翻译”，说“p是q的充分条件”就等同于说“在所有可能世界，‘如果p，那么q’都为真”。所以，正如努特所说：“说‘p不是q的充分条件’无非是说‘至少有一个可能世界，在其中p为真且q为假’。”（[8]，第432 页）那么，当我们说“语法是语义的充分条件”时，我们实际上说的是：

论题3：对于所有的可能世界，在其中如果有（足够丰富的）语法，那么有语义。14下文将“如果有（足够丰富的）语法，那么有语义”缩略为“如果有语法，那么有语义”。

那么，当我们说“语法不是语义的充分条件”，我们说的是：

论题4：存在一个可能世界，在其中有语法，但是缺乏语义。

在对上述说法进行“翻译”之后，我们不妨重新审视前提7。不难发现，前提7 说的是：对于所有在其中前提1-6 为真的可能世界集而言，存在一个可能世界，在其中有语法但是缺乏语义。所以，确如努特所说，沙非对于前提7 的解读过强。前提7 只蕴涵了一个关于某个可能世界的宣称，而并未像沙非所理解的那样，蕴涵一个关于所有可能世界的宣称。

然而，对于前提7 的解读错误是否意味着沙非对于前提7 的反驳就是错误的？或者说，对于前提7 的解读错误是否就意味着该模态论证不具有沙非所认为的逻辑漏洞？恐怕未必。该模态论证是否具有逻辑漏洞依赖于前提7 是否为假。前提7是否为假是一个形而上学问题，它和我们如何解读这个前提没有关系。即便沙非对于前提7 的解读是错误的，这并不蕴涵他对前提7 的反驳就一定是错误的。也就是说，前提7 仍然有为假的空间。所以，努特的结论下得太早：“沙非对于前提7 的解读是错误的”与“沙非对于前提7 的反驳是错误的”之间存在的鸿沟。从前者并不能推出后者。要判断后者是不是正确，努特需要提供额外的论证才行。然而，在努特的论文中，他并没有做到这一点。所以，单凭努特对沙非关于前提7解读方面的反驳，我们并没有充分的证据证明这个模态论证不具有沙非所说的逻辑漏洞。

既然努特没有给出任何证据来证明前提7 并非为假，那么，我们不妨考察沙非对于前提7 的反驳。如果我们能提供证据证明沙非对前提7 的反驳是正确的，那么我们就有证据证明前提7 为假，从而证明该模态论证确实存在沙非所说的逻辑漏洞。接下来，我们考察沙非是如何反驳前提7 的。

3.2 模态论证的逻辑漏洞

仍然按照前文的处理，我们把论域局限于在其中前提1-6 为真的可能世界集。那么，前提7 等同于：

存在一个可能世界，在其中有语法，但是缺乏语义。如果我们用SY代表“有语法”这个命题；用SE代表“有语义”这个命题，那么前提7 可以被表达为：◇(SY ∨¬SE)。沙非对于前提7 的反驳基于他对某个可能世界w1的构想。在w1上，语法恰好是语义的充分条件，即□(SY →SE)在w1上为真。换句话说，□(SY →SE)可能为真。假如沙非对于w1的构想是正确的，那么沙非实际上构造了如下反前提7 的论证：

前提9：□(SY →SE)可能为真。

前提10：如果□(SY →SE)可能为真，那么□(SY →SE)为真。（S5:◇□p →□p）

结论：□(SY →SE)为真。

这个论证的结论与前提7 针锋相对：后者宣称SY →SE可能为假；而前者宣称SY →SE必然为真。显而易见，两者之中只能有一个为真。但两者之中到底哪个为真哪个为假？这个问题的答案取决于前提9——□(SY →SE)的可能为真——是否成立。如果前提9 为真，那么CRA 模态论证确实存在逻辑漏洞。如果前提9 为假，那么CRA 模态论证不存在逻辑漏洞。所以，关键的问题是：沙非有理由证明前提9 为真吗？接下来，我们首先考察沙非是如何为前提9 作辩护的。

在其论文的两处，沙非似乎尝试为前提9 提供辩护。第一处，他说：“让我们考虑（consider）以下可能世界，w1：w1上所有其它属性和现实世界相同。我们假设（assume）w1 上有一个突现属性……。”（[12]，第234 页）在这个段落里，沙非所用的动词，如“考虑”，“假设”等都反映的是我们认知主体的思维活动。而认知主体的思维活动往往受制于其认知局限。我们所能考虑或假设的所谓的“可能性”并不一定是真正可能的。正如同我们对“哥德巴赫猜想可能为真”的考虑或假设不能证明哥德巴赫猜想可能为真一样，我们对于w1这个世界的考虑或假设并不能保证w1就是一个真正的可能世界。

第二处，沙非说：“这个属性（即，语法是语义的充分条件）的存在没有任何矛盾。”（[12]，第235 页）首先，我们必须区分“X没有矛盾”和“我们找不到X的矛盾”两种说法。对于前者的宣称需要我们提供正面证据来证明为何X无矛盾，而对于后者的宣称并不能提供这样的证据。还是以哥德巴赫猜想为例。我们不能找到“哥德巴赫猜想为真”这个命题的矛盾并不能说明哥德巴赫猜想没有矛盾；我们不能找到“哥德巴赫猜想为假”这个命题的矛盾也不能说明哥德巴赫猜想的否命题没有矛盾。作为一个数学命题，“哥德巴赫猜想为真”和“哥德巴赫猜想为假”两个命题之中必有一个是矛盾的。所以，我们不能发现它们的矛盾并不能证明这两个命题都是无矛盾的。而在沙非的论文中，要么他只是宣称“语法是语义的充分条件”没有矛盾而未能提供任何证据，要么他是把“我们找不到X的矛盾”当成了“X无矛盾”的证据。如果是前者，那么沙非的辩护是不充分的；如果是后者，那么沙非的做法是错误的。无论是哪种情况，沙非都没有为前提9提供充分的辩护。

其次，也是更为重要的一点，笔者将论证：沙非无法为前提9 提供辩护。我们仍然回到沙非的说辞。在提到“语法是语义的充分条件”的可能性时，沙非说：“这个属性（即，语法是语义的充分条件）的存在没有任何矛盾。”（[12]，第235 页）在这里，沙非似乎把形而上学可能性与逻辑的不矛盾性（也就是逻辑可能性）当成是同外延的。在其论文另外一处，沙非更为明显地将两者的外延等同起来。沙非说：“这一点要求证明SM逻辑为真……，但塞尔并没有给出任何理由证明SM必然为真。”15SM 是沙非论文中关于中文屋论证的某个论题。（参见[12]，第235 页）本文此处的讨论和SM 的内容无关，仅和沙非如何看待关于SM 的逻辑必然性和形而上学必然性有关。另外需要注意两点：一、沙非在此处似乎只谈了“逻辑为真”，但没有谈“逻辑必然真”。所以读者或许有如下反驳：沙非是将逻辑真与形而上学必然真的外延等同起来，而没有将逻辑必然真与形而上学必然真的外延等同起来。但是，对于任何命题而言，如果其逻辑为真，它一定是逻辑必然为真的。所以，如果沙非将逻辑真与形而上学必然真的外延等同起来，他也必须将逻辑必然真和形而上学必然真的外延等同起来。二、沙非将逻辑必然性和形而上学必然性等同起来，也就意味着他将逻辑可能性和形而上学可能性等同起来，因为同一意义上的可能性和必然性是相互定义的。所以在沙非那里，他实际上暗自引入了下述预设：

预设1

对于任一命题p，p是逻辑可能的（或必然的）当且仅当p是形而上学可能的（或必然的）。16请读者注意：这里所说的逻辑的不矛盾性（也就是逻辑的可能性）和逻辑的必然性并不是狭义的相对于某个模态逻辑系统而言的。相反，这里的逻辑可能性/必然性应当是指广义的，包括语义的、概念的、数学的等先天意义上的可能性/必然性。

此外，一般而言，逻辑可能性/必然性都是可以用先天性来刻画的。（[6]）说“p是逻辑可能的”即是说“p并非先天为假”；说“p是逻辑必然的”即是说“p先天为真”。所以说，沙非将形而上学可能性/必然性和逻辑可能性/必然性等同起来也就意味着他将形而上学可能性/必然性与先天性等同起来。换句话说，如果沙非暗自假设了预设1，那么他也就假设了预设1 的等价命题预设2：

预设2

对于任一命题p，p是形而上学必然为真的或形而上学必然为假的，当且仅当p的真值是先天可知的。17说“一个命题的真值先天可知（a priori knowable）”不等于说“一个命题的真值先天已知（a priori known）”。另，下文将把“真值先天可知的命题”简称为“先天命题”。

我们暂且不论这两个预设是否成立，而仅仅探讨在引入这两个预设的基础上，沙非必须要承担怎样的后果。18先天性和形而上学必然性外延等同的观点（即模态理性论的观点）是个争议较大的问题。康德以降，直至克里普克(S.Kripke)，模态理性论一直是广为接受的立场。但克里普克提出存在后天必然性以及先天偶然性的反例，用以反驳这个立场。然而，查莫斯(D.Chalmers)利用二维语义学试图消除克里普克式的反例，并重新恢复模态理性论。当然，克里普克反例本身有没有问题、查莫斯语义学是不是成功又是非常复杂的问题。本文无意在此讨论这些问题。本文的主要目的是挑战沙非的论证。本文的策略是接受沙非的所有预设，然后论证从这些预设出发并不能得到沙非想要的结论。笔者将论证，引入这两个预设将使得沙非无法为前提9 作出任何辩护，也就是说，他无法为“语法是语义的充分条件”的可能性提供辩护。

在模态系统S5 中，◇□p →□p和◇¬□p →¬□p都是公理或者定理。所以，“语法是语义的充分条件”，即，□(SY →SE)是一个若可能为真，则为真；若可能为假，则为假的命题。不难证明，任一若可能为真，则为真；若可能为假，则为假的命题也是一个要么必然真，要么必然假的命题。19说“p 可能为真，则为真；若可能为假，则为假”即是说“(◇p →p)∧(◇¬p →¬p)成立”；说“p 要么必然真要么必然假”即是说“□p ∧□¬p”成立。(◇p →p)∧(◇¬p →¬p)与□p ∨□¬p 等价关系的证明如下：首先，我们证明，为何(◇p →p)∧(◇¬p →¬p)蕴涵□p ∨□¬p。(◇p →p)∧(◇¬p →¬p)等价于(¬p →□¬p)∧(p →□p)。且□¬p →¬p 和□p →p 对于任意p 成立。因此，如果(¬p →□¬p)∧(p →□p)为真，¬p ↔□¬p 和p ↔□p 分别成立。又因为p ∨¬p 对于任意p 成立，因此，□p ∨□¬p 成立。所以，(◇p →p)∧(◇¬p →¬p)蕴涵□p∨□¬p。接下来，我们证明，为何□p∨□¬p 蕴涵(◇p →p)(◇¬p →¬p)。□p∨□¬p 等价于¬□p →□¬p。又因为¬□p 等价于◇¬p，且□¬p →¬p 对于任意p 成立，因此，¬□p →□¬p蕴涵◇¬p →¬p。同样，□p∨□¬p 又等价于¬□¬p →□p。¬□¬p 等价于◇p，且□p →p 对于任意p 成立，因此，¬□¬p →□p 蕴涵◇p →p。由此，□p∨□¬p 蕴涵(◇p →p)∧(◇¬p →¬p)。综上，(◇p →p)∧(◇¬p →¬p)与□p ∨□¬p 等价。又因为沙非引入了预设2，那么，沙非不得不承认□(SY →SE)是一个先天命题。

对于任一先天命题而言，其形而上学可能真当且仅当其逻辑可能真。所以，如果我们能为一个先天命题的可能性作出辩护，我们必须为其逻辑可能性作出辩护。此外，对于任何一个先天命题，其逻辑可能为真当且仅当其为真。所以，如果我们我们能为其逻辑可能性作出辩护，我们必须为其为真作出辩护。举例来说，哥德巴赫猜想就是一个先天命题，其形而上学可能为真当且仅当其逻辑可能为真；其逻辑可能为真当且仅当其为真。所以，如果我们有证据说明哥德巴赫猜想可能为真，我们必须有证据说明其为真。换句话说，如果我们无法判断哥德巴赫猜想的真值，我们就无法判断它是否可能为真。

□(SY →SE)这个命题也面临同样的情况：由于沙非设定了预设2，所以沙非不得不承认□(SY →SE)是一个先天命题。那么问题就出现了：如果要为其形而上学可能性提供辩护，我们必须有证据为其逻辑可能性作出辩护；而要为其逻辑可能性作出辩护，我们必须有证据证明其为真。所以，如果我们无法判断其真值，我们就无法判断其是否是逻辑可能的，也无法藉由其逻辑可能性为其形而上学可能性作出辩护。沙非显然没有证据证明□(SY →SE)为真，否则他就能利用该命题为真的证据直接驳斥模态论证的前提7，从而证明该论证不可靠。他又何必转而诉诸该命题为真的可能性来达到目的呢？所以，在这种情况下，由于他缺乏□(SY →SE)为真的证据，他无法这个命题的可能性提供任何辩护。

最后，我们做个小结。关于对前提7 的解读，沙非确实犯错了。但是，关于对前提7 的反驳，沙非和努特都过早地下了结论。一方面，努特并没有给出证据说明前提7 为真。另一方面，沙非试图通过证明前提9 为真来反驳前提7。但他没有，甚至也不能提供充分的证据来前提9 为真。所以说，仅凭沙非和努特的论证，我们既没有关于前提7 为真的证据，也没有关于前提7 为假的证据。因此，我们无法判断沙非提供的模态论证是不是有逻辑漏洞，也无法借助于这个模态论证来证明CRA 错在何处。

4 对沙非模态论证模式的诊断

在这一部分中，笔者将以沙非对CRA 模态论证的反驳为例，提取出哲学论辩过程中一种常见的模态论证模式。笔者认为这种论证模式由于其模态前提难以得到辩护，因此在实际过程中并无实用价值。这种论辩过程往往以以下模式进行：论辩者A提出一个模态宣称：必然p为真（□p）。A的反对者B宣称：p可能为假（◇¬p）。为了反驳B（或者支持A），论辩者C（也有可能是A自己）往往诉诸“□p为真”的可能性，从而提出以下模态前提：□p可能为真（◇□p）。由于在模态系统S5 中，◇□p →□p是系统公理，所以论辩者C可以得出“□p为真（□p）”的结论。其各自观点和论证形式如表1 所示：

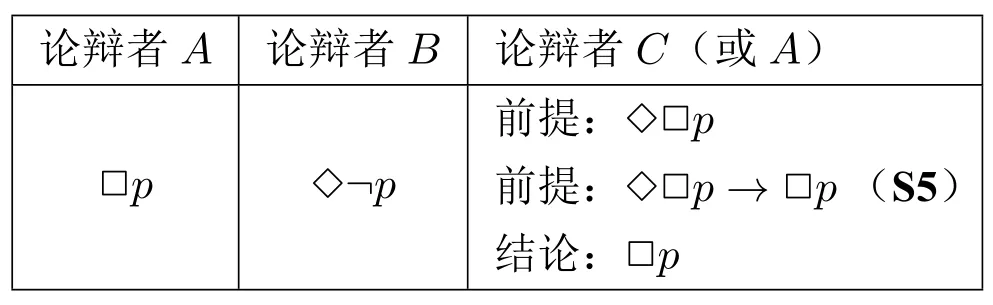
表1

以强人工智能的支持者（对应上表论辩者A）和塞尔（对应上表论辩者B）的论辩过程为例，前者认为，在每一个可能世界里，一旦屋中人按中文语法进行输入和输出，那么他是理解中文语义的（即□(SY →SE)）。20这里所说的可能世界仍然如本文第二部分所声明的那样，是在其中前提1-6 为真的可能世界。而后者认为，存在一个可能世界，在其中屋中人按语法操作，但实际上他并不理解语义（即◇(SY ∧¬SE)）。为了反驳塞尔，沙非（对应上表论辩者C）提出：存在一个可能世界，对语法的操作必然引发对语义的理解（即◇□(SY →SE)），并由该前提出发得出□(SY →SE)的结论。

类似的模态论证模式在其他领域并不鲜见。在心灵哲学领域关于现象属性是否是物理属性的论辩中，物理主义者和二元论者往往采用这样的论证模式。21本文所说的“物理主义”指的是随附性物理主义。该版本的物理主义所有物理主义类型中最弱的一类。物理主义者（对应上表论辩者A）坚持：一旦这个世界的微观物理事实被固定住，那么这个世界的现象事实也被固定住（如果用P和Q分别表示现实世界的微观物理事实和现象事实，那么物理主义者认为□(P →Q)）。而二元论者（对应上表论辩者B）认为存在这种可能性：即便微观物理事实和现实世界相同，某些现象事实仍然和现实世界是不同的（即，二元论者认为◇(P ∧¬Q)），比如说在某个可能世界上存在僵尸或者感受性质反转的情况。为了反驳二元论者的观点，一部分物理主义者（对应上表论辩者C）试图利用□(P →Q)的可能性来击败二元论者。他们采用了如下的论证：

前提1：□(P →Q)可能为真。

前提2：对于任一命题p，◇□p →□p为真。

结论：□(P →Q)为真。22采用该论证形式的反二元论论证参见[4,7,10,15]。

形而上学中，有神论者（对应上表论辩者A）认为：必然地，存在完美物。无神论者（对应上表论辩者B）认为：可能地，不存在完美物。于是部分有神论者认为（对应上表论辩者C）试图诉诸一个必然完美物的可能性击败对手。（参见[9]）我们可以把这些例子列举在表2 中：

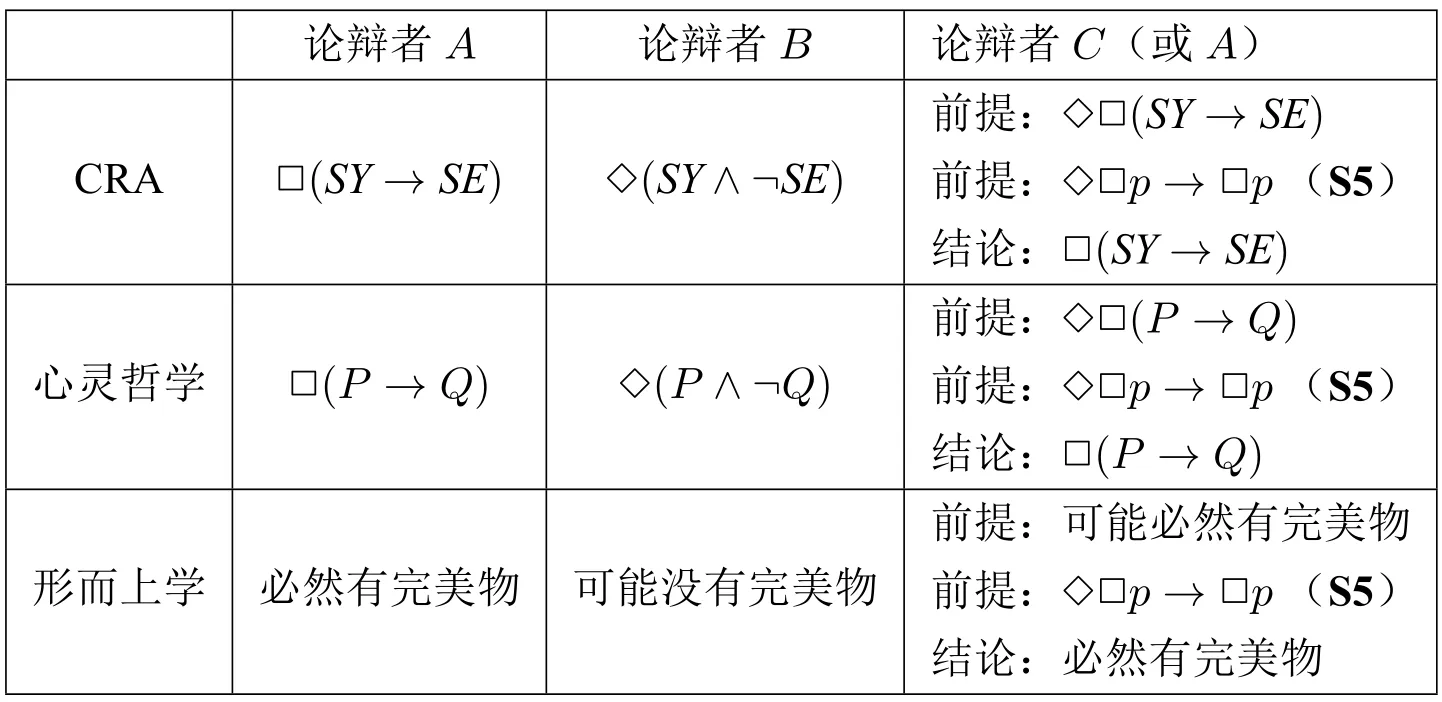
表2

这些论辩过程的核心在于论辩的双方都诉诸于一个模态宣称：论辩者B诉诸于◇¬p；论辩者C诉诸于◇□p。那么，一个自然而然的问题就是，论辩双方如何为其模态宣称提供辩护？尤其是论辩者C，如何能为□p的可能性提供辩护？自然地，如果要提供模态辩护，我们必须诉诸某个模态认知理论。在模态知识论领域，比较成熟的模态认知理论有理性论路线下的可设想性理论；经验论路线下的相似性理论；反事实理论等。23关于可设想性理论，参见[2]；关于相似性理论，参见[11]；关于反事实理论，参见[16]。其中查莫斯的可设想性理论的应用最为广泛。24这个理论的核心观点其实也是沙非为前提9 提供辩护时所暗自使用的，即便他没有明确表示他使用的是可设想性理论。该理论也是表2 中所列举的几个模态论辩中学者们试图提供模态辩护时所使用的工具。

可设想性理论的核心观点是：可设想性蕴涵可能性。那么，什么叫作可设想性？查莫斯抛弃了传统的将其定义成“可想象性”的做法，而将其定义为“逻辑可能性”（也就是逻辑上的无矛盾性，或者说，并非先天为假）。所以，查式可设想性理论的核心观点实际是前文提及的预设1 中从左到右的蕴涵关系：逻辑可能性蕴涵形而上学可能性（或者说，对于任一命题p，如果p是逻辑可能的，那么p是形而上学可能的）。值得一提的是，查式可设想性理论的核心观点仅仅是一个形而上学的宣称：它仅仅陈述了两种可能性之间存在蕴涵关系。它并未宣称也无须承诺我们认知主体和逻辑可能性在认知上具有什么关系。然而，当查式可设想性理论被当作一套模态认知理论被用于模态辩护时，它就对我们关于逻辑可能性的认知状况提出了要求：只有我们在具有一定的关于逻辑可能性的知识时，才有使用这个理论的条件。也就是说，当我们试图利用可设想性理论为宣称◇p提供辩护时，我们必须有证据证明p是逻辑可能的；当我们试图利用可设想性理论为宣称◇□p提供辩护时，我们必须有证据证明□p是逻辑可能的。反过来说，如果我们不具备关于□p的逻辑可能性的辩护，我们就无法利用可设想性理论为□p的可能性提供辩护。然而，可设想性理论的使用者，比如表2 中的论辩者C往往忽略了这个认知条件。由于对这个条件的忽略，论辩者C误以为他们能为□p的可能性提供辩护，但实际上并不能做到这一点。

前文已经提及，在模态系统S5 中，任一命题□p都满足◇□p →□p和◇¬□p →¬□p。所以，任一命题□p都是要么必然真要么假的命题。根据预设2，我们可以得出，任一命题□p都是一个先天命题。对于任何一个先天命题，我们对于其逻辑可能性的辩护要求我们有证据证明其为真。所以，对于任一命题□p，如果我们有证据证明其是逻辑可能的，我们必须有证据证明其为真。但是，在论辩过程中，正是因为我们没有证据证明□p为真，我们才转而诉诸于□p的逻辑可能性；我们才希望以□p的逻辑可能性为中介，帮助我们获知□p的形而上学可能性以及其真值。如果我们已有证据证明□p为真，我们何必还需要知道□p的逻辑可能性以及形而上学可能性呢？所以说，在不具有关于□p为真的证据的情况下，我们是不具备使用查式可设想性理论的认知条件的，也无法利用该理论为□p的可能性提供任何辩护。回到表2 中的例子，沙非无法为◇□(SY →SE)提供辩护；物理主义者无法为◇□(P →Q)提供辩护；有神论者无法为“可能必然有完美物”提供辩护。这些模态论证在论辩过程中无法为哲学讨论作出任何推进。

某些模态前提难以通过查式可设想性理论得到辩护并不是新鲜的观点。布鲁克内（A.Brueckner）和沃利（S.Worley）就提出，存在一些命题，由于我们缺乏关于其逻辑可能性的证据，我们就无法利用查式可设想性理论为这些命题的形而上学可能性提供任何辩护。（参见[1,17]）但他们并没有具体指出，究竟哪些模态命题的逻辑可能性无法得到辩护，以及为何这些命题的逻辑可能性无法得到辩护。由于这方面工作的缺乏，面对一个具体的模态前提，我们就无从判断我们是否具有为其逻辑可能性以及形而上学可能性提供辩护的能力。在本文中，笔者从CRA 的模态论证出发，以哲学各分支领域的模态论证为例，指出究竟是哪些模态前提难以得到辩护，并解释了其难以被辩护的原因。25当然，笔者在本文中做了一个非常重要的预设：模态辩护需要使用查式可设想性理论。此处，笔者简要说明为何要做这个预设。第一，查式可设想性理论是沙非在其论文中暗自使用的理论。笔者的目的是要反驳沙非的结论，那么比较好的策略是承认他的所有预设，从其中推出让人难以接受的结论；而不是从他的预设开始就提出反对意见。第二，查式可设想性理论是哲学分支各领域的学者们试图为模态前提提供辩护时使用得最多的理论，所以预设这个理论可以得出一个具有普遍性的结论。

5 结语

本文选取了沙非模态版CRA 作为讨论对象，并分别评价了沙非对该论证的反驳以及努特对沙非的回应。本文指出，恰如努特所说，沙非对于该论证前提7的解读是错误的。但是，关于前提7 是否为假的讨论，沙非和努特都没有给出充分的证据。进一步，笔者讨论了沙非反驳前提7 所采用的模态论证。笔者指出沙非无法为这个论证的模态前提作出辩护。最后，笔者以沙非对模态版CRA 对所采用的反驳论证为例，提炼出一种一般化的在哲学论辩中常见的模态论证模式。笔者指出，我们难以为这种论辩模式中涉及的模态前提提供辩护。因此，这种论证模式在论辩中并无实用价值。