紧致性与拉姆塞定理*

杨跃

1 引言：谈谈紧致性

语言及其指称的讨论在哲学中甚至在生活中都屡见不鲜。为了不离题太远，我们只考察一个比较容易刻画的问题：能不能用语言精确地描述一个数学结构？这样说有些模糊，因为“语言”和“精确地描述”都可能有不同的解读。我们必须引进数理逻辑的术语把问题更准确地叙述成：

问题：是否存在一个（一阶）语句集S，使得任何两个满足S的数学结构都是同构的？

答案不难，只需对数理逻辑稍有了解，但有意思的是结论依赖于所讨论结构（或“世界”）的大小。

断言1如果一个数学结构A中只有有穷多个元素，则满足上述问题条件的语句集S存在；甚至只要一个语句就够了，即，存在单个语句σ，使得A满足σ，且任何满足σ的结构B都同构于A。

证明思路很自然：先考虑结构涉及的关系和函数是有穷的情形。我们只需把A里面元素之间的关系和函数列成一张大表，可以证明这张表是有穷的。σ基本上就是把这张表的所有信息记录下来。如果结构涉及的关系和函数是无穷的，则需要先论证其中存在一个有穷子集，只要在子集中的关系和函数上表现相同，则在所有关系和函数上都表现相同，这样就归约到了第一种情形。

那么无穷的结构呢？

断言2如果一个数学结构A中有无穷多个元素，则不存在一个的语句集S（这里S可以是无穷集合），使得A满足S，且任何满足S的结构B都同构于A。

断言2 的证明要用到数理逻辑中的紧致性定理（Compactness），也就引出了我们的主题。

数理逻辑中的紧致性定理：如果一个（一阶）语句集S的任何有穷子集都是可满足的，则S本身也是可满足的。

利用紧致性定理，可以证明：如果结构A有无穷多个元素，则存在结构B，B的基数大于A（因而不同构于A），且和A满足同样的语句集。细心的读者可能会问，难道不能把结构的基数也叙述出来，例如要求A是可数无穷的吗？问题就在这里，在“一阶”语言中，我们只能谈论结构里的个体，而无法断言是否存在结构的子集或定义在结构上的函数，因而也无法谈论结构的基数。

让我们简单回顾一下上述紧致性定理的历史。最早的版本来自哥德尔的1929年的博士论文。哥德尔在论文中证明了一阶逻辑的完全性，而紧致性定理是完全性定理的推论。但哥德尔只论证了紧致性定理的可数情形，因为他不需要更一般的情形。哥德尔完全性定理的证明用到了一个“人们熟知的论证”，他没有说是什么，后人猜测为类似于弱柯尼西引理（Weak König Lemma）式的论证。弱柯尼西引理叙述为任何无穷的二叉树必有无穷支。显然它对有穷分叉的树都成立。后来人们发现，弱柯尼西引理也是紧致性的一种表现形式。

下面我们小结一下紧致性几种形式，顺便进一步解释一下弱柯尼西引理。

· 很多人第一次接触到“紧致性”是在数学分析中学Heine-Borel 定理的时候，该定理说实数上[0,1]区间上任一开覆盖必有有穷子覆盖。

· 上文提到的数理逻辑中的紧致性定理：如果一个语句集S的任何有穷子集都是可满足的，则S本身也是可满足的。

· 还有弱柯尼西引理：任何无穷的二叉树必有无穷支。

这几种形式表面上看完全不同，但背后都涉及“有穷-无穷”之间的联系。粗略地说，Heine-Borel 定理把无穷覆盖归约到某个有穷覆盖；逻辑中的紧致性定理把无穷语句集是否能被满足的问题归约为某个有穷集上的问题。而最后提到的弱柯尼西引理则需要解释一下。

首先，我们只考察可数的二叉树，从而可以把二叉树T视为有穷0-1 串{0,1}＜ω的子集，且满足下述封闭性：如果σ ∈T且τ是σ的前节，则τ ∈T。T里的元素称为节点。我们称一棵树T是无穷的，如果T作为节点的集合是无穷的。T上的一“支”就是它的一个子集B使得对任何σ,τ ∈B，或者σ是τ的前节，或者τ是σ的前节。弱柯尼西引理看上去太显然了，几乎不用证明大家也会相信。难怪有本学术著作给出了下面类似童话的“证明”：从前，有一只老虎和一个猎人，他们最开始都在树T的根节点上，老虎的背后就是T上无穷多的节点。T是二叉的，所以老虎后面有两条路，它该选那一条呢？如果左边的路通向无穷多节点（聪明的老虎当然能辨别有穷和无穷），它就向左跑；如果T的左一半只有有穷多节点，那它右一半就必有无穷多节点，那么老虎就向右跑。老虎跑一步，猎人当然就追一步。但每次老虎后面都有无穷多节点，所以猎人总追不上它。最后，他们跑过的节点就是我们要找的无穷支。

回到前面的紧致性。一般来说（这里我们有些模糊，因为略过了对背景语言的讨论），描述一个集合是无穷的需要两个无界量词，即，对任意n个点的子集，都存在一个不在该子集中的新点。但如果我们想知道一个二叉树T是否是无穷的，我们只要说，对任意n，在第n层上都存在一个T节点。但二叉树第n层至多只有2n个节点，所以第二个存在量词是有界量词。这样，紧致性体现在帮我们省掉了一个量词。也许有人会说这是树对前节封闭性造成的，不需要紧致性。但假如我们考察一下无穷分支的树，它也有对前节的封闭性，但是无穷树却可以没有无穷支！

2 紧致性与数学哲学

众所周知，数学哲学的基本问题之一是：既然数学对象不存在于物理世界（时空）中，那么数学知识是关于什么的知识？按照对数学对象本体论上的定位，数学哲学家大概归属于以下两大阵营：实在论（或柏拉图主义）和反实在论（或虚构主义）。

在一些反实在论者看来，整个数学知识应该被划分成两部分，一部分是关于有穷世界的知识（特别是在物理世界中有实例的部分），这部分知识是有意义的，也有真假；而关于无穷世界的部分（特别是实无穷的那部分），都是“虚构”的，这部分知识或许有用，但它们没有意义，也谈不上真假。

然而，如果人们认可紧致性定理这类“人们熟知的论证”，反实在论者在有穷与无穷之间画的这条线就显得过于人为，画这条线的动机不是出于数学的内在需要，而是为了贯彻哲学上的某种世界观。如果我们承认紧致性定理，则也要承认有穷世界和无穷世界是有联系的。紧致性定理有如下的推论

紧致性定理推论

如果一个（一阶）语句集有任意大的有穷模型，则它必有一个无穷模型。

例如，我们考察代数里群的结构，令σ为∀x∀y(x·y=y·x)，即满足σ的都是交换群。由于有任意有穷阶的交换群存在，紧致性定理告诉我们一定会有无穷的交换群存在。当然这个例子数学上过于简单，我们不需要通过紧致性定理也知道有无穷的交换群存在。数理逻辑里面有很多更自然的类似例子，但由于涉及更多的背景知识（如算术的非标准模型），我们这里不想多谈。我们想强调的是：如果一个人承认关于有穷世界的陈述是有意义的，不能虚构。那他或她也必须承认，我们也不能任意地去“虚构”无穷世界的事实。例如，你不可能让一个在有穷世界里都真的语句σ，在所有的无穷世界里都假。在这个意义上，σ在有穷世界中的意义会赋予它在某些无穷世界中的意义。

当然反实在论者几乎肯定不接受紧致性定理，因为紧致性定理表述中（至少在我们提到的这三个版本里）都涉及了无穷本身。那么有没有不接受紧致性定理理由呢？没有紧致性的数学会是什么样子呢？这就引出了我们下一个话题——反推数学（Reverse Mathematics）。反推数学可以告诉我们哪些数学定理是不需要紧致性定理的，哪些是必需要紧致性定理的。

最后再评论一句，对我来说，实在论与反实在论的根本分歧不在于什么是实在的什么是虚构的，而是在于承认不承认“整个世界”（无论是物理的还是数学的）背后有没有一个统一的规律。（大多数的）实在论者会认为有一套贯穿“整个世界”的理性规律（或逻辑），这些规律是客观的，不是我们虚构的。而且我们没有必要去区分满足这些规律的对象是否在时空中存在。以牛顿定律（或其他物理定律和方程）为例，我们没有必要去在日月星辰和物理课本上的质点滑块之间画线。而（多数的）反实在论者会强调规律无非是感官经验的总结，像无穷集合这样的对象由于不能被我们经验到，所以不可能存在关于它们的所谓规律。

3 反推数学简介

反推数学创立于20 世纪70 年代，到现在接近半个世纪了。但恐怕对大多数读者来说，反推数学依然是一个陌生的名词。因此有必要做一些简单的介绍。

反推数学关心的是数学定理的“相对强度”。例如，我们比较如下两个代数里的命题：P:“任意交换环都有极大理想”和Q:“任意交换环都有素理想”。由于极大理想都是素理想，所以P ⇒Q。事实上，在大学本科教材里，素理想的存在往往就是通过极大理想的存在来论证的。那Q是否真比P弱呢？即，有没有呢？或者说，有没有可能一个交换环里只有素理想而没有极大理想呢？

当然，如果我们每次都比较一对数学定理P和Q，那效率是非常低下的。事实上，反推数学做的往往不是直接比较P和Q，而是建立严格的逻辑公理系统分层Γ0＜Γ1＜...，来论证Γi能证Q但不能证P。这里每个Γi都代表一个逻辑系统，通常是某个数学基础研究中常见系统（如，一阶算术、二阶算术或集合论）的子系统，其中的＜一般表示左边的系统的逻辑后承是右边系统逻辑后承的真子集。而论证Γi不能证P的方法常常是找到某个j ＞i然后用P证Γj；通俗地说，就是在逻辑公理系统里建立一把尺子，用它去量数学中的定理，如果P的刻度是3 而Q的刻度是2，则这样做的好处一是逻辑系统的强弱相对来说更容易用数理逻辑中的工具（如对角线法，或用不完全性定理）来论证；二是逻辑往往为各个不同的学科提供了一个共同的舞台，直接比较两个不同领域里的（如图论的和概率的）定理恐怕要花很大的功夫先去统一语言和符号，因而较为困难，但我们却可以通过把它们分别和逻辑系统比较来间接达到我们的目的。

注意：上面的讨论包括两个方向，我们一方面论证Γi能证Q，即用公理去证定理，这是大家所熟悉的“正推”；另一方面，我们也论证P可以证Γj，即用定理去证公理。这是反推（reverse）二字的由来。在反推数学的文献里，常常会把反推数学的目标定为：对经典（可数）数学中的定理，找出其证明所需的公理。这样说没有错，反推数学的确是想为定理找出精确的公理“量度”。但这种说法也引来一些诘难：数学贵在创新，而反推数学在定理之间或定理与公理之间搞来搞去，有悖于数学的创新原则。这些诘难实际上源于一种典型的误解。“典型”是因为同样的诘难也经常被用在机器证明和构造性数学等学科头上。为什么说它是误解，原因是为了实现反推的目标，常常需要找到新的证明，这恰恰是创新。在反推数学研究中，循规蹈矩地把经典证明分析一遍就完成任务的论文是不受关注的；大家欣赏的依旧是那些“匪夷所思”的创新证明。

那么是不是每一对P和Q都可以比较呢？或者说是不是所有的数学定理的强度都能被“量”出来呢？这在反推数学发展史上是个很有意思的问题。让我们先对反推数学多一些了解，然后再回到这个问题。

反推数学使用的是二阶算术的子系统（也称为片段fragments)来作为衡量定理的尺度。这里一方面有历史原因，因为二阶算术是希尔伯特比较关注的系统之一。另一方面的原因是在数学基础里常见的三个系统当中，一阶算术只谈论初等数论命题，逻辑中形式系统能够被编码为自然数，所以逻辑学与一阶算术关系紧密。但如果把数学里一般的内容都换成自然数来讨论是既费力又不自然；集合论由于涵盖了几乎所有数学，它的子系统通常跨度非常大，容易漏掉细微的差别；而二阶算术介于两者之间，其中可以比较自然地讨论组合和代数的问题，通过编码也可以讨论数学分析和微分方程中的问题，正好用来衡量经典数学中的定理。

在二阶算术中，人们不仅可以谈论个别的自然数，也可以谈论自然数的集合。让我们稍微多解释几句：在二阶算术中有两组不同的变元和量词，一组是用来谈论自然数的，例如，∀m∃n(m ＜n)中的量词都是管辖自然数m和n的，它是一个“一阶”语句；另一组则是谈论集合的，当然这两组变元和量词可以在同一语句内出现，例如，所谓“良序原则”（所有非空集都有最小元）就可以用二阶算术语句表示为：

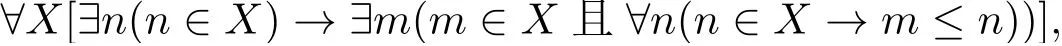
其中∀X是二阶的，X代表的是自然数的子集，而中括号内的除了二阶参数X之外都是一阶的，m和n代表的是个体自然数。反推数学中最常用的尺度是如下五大子系统：

（第一层或基本层）RCA0（只承认可计算的集合或函数存在）

（第二层）WKL0:RCA0加上“弱柯尼西引理”。即，承认紧致性定理。

（第三层）ACA0（承认一阶算术可定义的集合存在）。

（第四、五层）ATR0和-CA0。

由于篇幅关系我们不解释英文缩写的涵义，而是简略说一下分层的思想。利用二阶存在量词，我们可以直接断言某类自然数的子集存在。系统越强，它（的模型）里面的集合就越多。比如，第一层的系统里只有可计算的集合存在；而第三层则包括了所有在一阶算术内可定义的集合；第五层就更多了；这三层是借助可定义性来描述的。而第二层和第四层则是借助数学工具来间接描述的，例如，第二层就是断言像二叉树上无穷支那样的集合是存在的。在第一层RCA0的世界里，只有可计算的集合存在。而递归论中有定理表明，存在一个递归的二叉树T没有无穷的递归支。这样，生活在第一层上的人会看到这棵树T，但却看不到它的任何无穷支。在下文中，我们只涉及前三层，重点围绕着第二层。所以第四、第五层就不提了。

反推数学自从1970 年代创立以来，直到2000 年，主要结果都是把数学定理归类到这五大子系统中去。反推数学的标准参考书，辛普森的专著（[6]）就是对这些成果的一个全面总结。例如，Heine-Borel 定理，哥德尔完全性定理，素理想存在定理等等都等价于第二层的WKL0。大学本科里所涉及的数学内容，几乎都能被这五大子系统度量出来。有人开玩笑说：“人们惊奇地发现，从古到今数学家只证了五个定理”。这就向反推数学家提出了挑战，要么给出一个哲学上的解释，为什么数学上定理的强度会排得这么整齐；要么发现不在这五大系统里的重要的数学定理。这就引出了我们下一节——拉姆塞定理。

4 拉姆塞定理

拉姆塞（F.P.Ramsey），是英国的数学家、哲学家兼经济学家。虽然英年早逝，但却在很多领域都做出了杰出的贡献。拉姆塞定理是他在论文[4]（《形式逻辑上的一个问题》）中证明的。论文提交于1928 年，发表于1930 年。拉姆塞文章的主旨是逻辑中的判定性问题，只是为了技术上的需要他才先证了拉姆塞定理；而如今该定理已成为组合数学中的一个重要分支，称为拉姆塞理论。

拉姆塞定理：对任一f:[N]n →{0,1,...,k-1}，都存在一个无穷的齐性（或称同色homogeneous set）H ⊆N，即，f限制在[H]n是常数。（这里，对A ⊆N,符号[A]n表示A的n-元子集的集合。）

通常称f为“一个k-染色”。上述版本记为，我们主要关心——格点上的拉姆塞定理。看一个简单的例子，对自然数x ＜y，我们定义如下的染色f：

则所有素数的集合是一个无穷的染0 的同色集，因为任意一对素数显然互素；而由2 的各次幂组成的集合{2,4,8,16,...}则是一个无穷的染1 的同色集，因为任意一对都有公因子2。

考察自然数二元子集上的一个红蓝染色f。首先我们先“捋顺尾巴”：取a0=0。固定住a0。先选一个无穷集B0，使得对所有b ∈B0，f(a0,b)同色。这样的B0总是有的（想想上面老虎背后的森林，道理是一样的）。无妨设对任一b ∈B0，f(a0,b)都是红色。此时，让我们称a0为“红点”。从现在起只考虑B0里的元素。令a1为B0的最小元，再选无穷集B1⊂B0使得对所有b ∈B1，f(a1,b)同色，让我们假设他们都是蓝色，我们就称a1为一个“蓝点”。这样一直做下去，我们每次都把“尾巴”（即，集合B0,B1,...等等）缩小，使得“尾巴”里的元素与前面的点（即a0,a1,...等等）都分别地染同一种颜色，与此同时，得到一个红蓝点的无穷序列（即序列(a0,a1,...)）。红点和蓝点组成的子序列至少有一个是无穷的。那就是我们要的H。

顺带评论一下：以上的证明直观上很简单，但同色集H的复杂度会很高。为什么呢？因为，在拿B0的时候，我们需要知道和a0配起来是红的有无穷多还是蓝的有无穷多，这样B0就比染色f“多了两个量词”（见前面对弱柯尼西引理的讨论）。接下来，B1又比B0“多两个量词”，这样一直做下去，拿到的红蓝点的序列就涉及了“无穷多量词”。这还没完，在红蓝点序列中，我们还要再分一次，挑出一个无穷集来，这又（在无穷个量词之上）“多两个量词”。总之，从可定义的角度看，这样拿到的同色集H是非常复杂的。

拉姆塞定理是组合数学里带有哲学意义的重要定理之一。我们可以把它解读成：任何混乱（即染色）中都有某种秩序（即同色集）。有数学家评论说：拉姆塞定理表明“绝对混乱的系统是不存在的”。这样的解读多少带一些理性乐观主义的味道。

反推数学中对拉姆塞定理的研究起始于加库什1972 年的文章[2]。加库什是从递归数学的角度来研究拉姆塞定理的，但他的结果可以直接“翻译”成反推数学的结果。下面我们给出用反推数学语言表达的加库什结果：

加库什定理

·对n,k ＞2,等价于ACA0。换句话说，除了，其他版本的拉姆塞定理都恰好处在第三层。

·ACA0蕴涵；但WKL0不蕴涵。换句话说，在第三层或在第三层之下，但不在第二层更不在第二层之下。

对熟悉数理逻辑的读者来说，加库什定理的原版也非常有意思。加库什证明了：对来说（1）任何递归的染色都有的同色集；（2）存在一个递归染色没有的同色集。我们前面说过，语句大致对应无穷集合的表述。因此，加库什定理说明，虽然同色集存在，但如果想要把它“找到”则非要借助无穷这一概念不可。结合拉姆塞定理的意义，我们可以进一步引申一下：加库什定理告诉我们，尽管混乱中有秩序，但只有站在更高的水平上才看得到。

加库什之后，这一领域沉寂了20 多年，直到1995 年，西塔潘和斯莱曼（[5]）才把它重新唤醒：

西塔潘-斯莱曼定理

西塔潘-斯莱曼定理的证明巧妙利用了树的性质，于是西塔潘提出了后来以他命名的“西塔潘猜想”：蕴涵WKL0。即要想证明格点拉姆塞定理，非得用弱柯尼西引理不可，换句话说，紧致性定理是格点拉姆塞定理的必要条件。从反推数学的尺度上看，西塔潘猜想叙述为：的强度严格介于第二层和第三层之间。虽然格点拉姆塞定理不对应五大子系统中的任何一个，但西塔潘猜想意味着只需在尺子上多添一个刻度就可以了。

从此，西塔潘猜想成为反推数学里人人关心的问题，几乎所有做反推数学的人都尝试过。为了它还不止一次专门召开国际研讨会，参会人员除了递归论和反推数学之外，还包括集合论、证明论、组合数学和计算机科学等领域的研究人员。大家尝试过各种各样的方法，如力迫法、非标准模型和概率等等。各种尝试中有一个共同点：分而治之；也就是说把分解成一些比它还弱的组合原理，通过搞清楚这些弱的组合原理来解决西塔潘猜想。于是便产生了下面的图1，大家把这张图称为反推数学“动物园”1这张图也包括了一些强于 的组合原理。另外，这张图也已过时，有兴趣的读者可以浏览网页https://rmzoo.math.uconn.edu/。。图里面的节点都是组合原理或逻辑子系统。对拉姆塞定理和反推数学有兴趣的读者可以阅读赫施菲尔德的讲义（[1]）。

西塔潘猜想最终是由我国年轻数学家刘路2文章是用“笔名”刘嘉忆发表的。否证的（[3]）。

刘路定理

刘路结果的意义一方面是技术上有重大创新，他的证明方法已被很多学者用来解决了很多的疑难问题；另一方面，刘路的结果确认了存在与五大子系统不可比的重要定理。这样，连同其他种种“动物学”的成果，说明反推数学旧有的“范式”已经不适用了。数学定理强度的分类肯定不会像一把直尺那样简单，而应该是一个偏序结构。这一偏序结构到底是什么样子呢，有没有它的内在规律呢？它至少不应该像动物园那样混乱吧。有没有一个自然的、合理的分类法是目前的对反推数学和数学哲学的挑战之一。

图1：反推数学“动物园”