Correlating common breakage modes with impact breakage and ball milling of cement clinker and chromite

Mahmut Camalan

Mining Engineering Department,Middle East Technical University,Ankara 06800,Turkey

ABSTRACT Understanding the mechanisms of the breakage of ore particles is important to predict the particle size distribution in size reduction operations.This paper aims to show the presence of common breakage modes in impact breakage and ball milling of the cement clinker and chromite samples.For that purpose,narrow size fractions of the two samples were broken in a drop-weight tester or ball mill by changing the degree of applied energy.Then the resultant size distributions were evaluated to seek evidence for the common breakage modes.The results showed that increasing the breakage energy will produce a systematic change in the shapes of the size distributions,suggesting a sequential set of breakage modes.The breakage is initially due to tensile stresses at low breakage energies and compressive stresses at high breakage energies.Further studies should be done to assess if these breakage modes occur at sizereduction of different ores.

Keywords:Progeny distribution Impact breakage Ball mill Self-similarity Breakage modes Cone of fines

1.Introduction

One important objective for mineral engineers is to predict product size spectra as a function of the applied energy in sizereduction equipment.For that purpose,energy-based models were initially developed to predict only a single size index of the breakage product as a function of the energy input [1].The population balance model (PBM),on the other hand,is used to predict the overall product size spectra by incorporating the semi-empirical selection function and breakage function in rigorous models[2,3].As the PBM is a semi-empirical method,its predictive power is limited to the feed size spectra and feed composition as well as the mill environment.Most importantly,neither energy-based models nor the PBM can fully explain how the particle breaks after applying a given amount of breakage energy.A testable hypothesis will be quite useful to develop fundamental relations between the product size spectra and the applied energy.

The breakage of a particle in a grinding mill can be accomplished through (1) impact loading,(2) abrading or (3) chipping the particle with a steel ball [3].These breakage mechanisms mimic either the collinear or non-collinear(eccentric)impact configurations that are defined for analysing the mechanics of two body impacts [4].The collinear impact configuration is quite similar to the impact loading.It will prevail if the center of mass of each colliding body lies on the normal line of the common plane that is tangent to the colliding bodies at the contact point.The collinear collision generates a force or impulse inside the particle,causing the disintegration of the particle.On the other hand,abrasion and chipping can be regarded as an eccentric impact configuration where at least the center of mass of one colliding body does not lie on the normal line of the common tangent plane at the contact point.This configuration causes a fraction of the impulse to go inside the particle; therefore,it causes less damage than the collinear impact.Abrasion and chipping,in other words,may be equivalent to impact with low impulse.

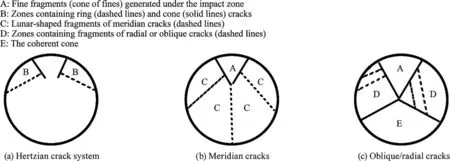
Fig.1.Simple illustrations for the Hertzian crack system,meridian cracks,and oblique/radial cracks.

Four common breakage modes are observed to develop successively with increasing strain rate (or congruently the applied energy) in single-or double-sided impact or compression:(1)Hertzian cracking [5–7]; (2) meridian/secondary cracking [5,6,8–14]; (3) oblique/radial cracking [5,6,12]; and (4) shattering[5,6,15].These modes successively proceed to generate more progeny particles with an increasingly wider size distribution[16,17].Hertzian cracking is the brittle-elastic response of the material at very low strain rates,which will generate ring and cone cracks under the contact area(Fig.1a).However,Hertzian cracking does not contribute to the complete failure of a particle [5].Additional increases in the strain rate will result in the formation of a small mass of fine fragments under the contact zone,named as the cone of fines.The formation of this volume is linked to the intensified compressive stresses initiating at the contact zone[5,8,14].The higher strain rates will enlarge the cone of fines while resulting in the evolution of tensile stresses around this cone[18].These tensile stresses form meridian cracks(Fig.1b),which generate fragments like the shapes of orange slices or lunes having similar dimensions.Meanwhile,secondary cracks perpendicular to the meridian cracks may evolve after the latter cracks are completely formed [9,10,19].If the strain rate is increased further,the cone of fines will enlarge while the oblique/radial cracks(Fig.1c)replace the meridian/secondary cracks.The oblique/radial cracking will result in the formation of fine particles and a large coherent cone,which cannot easily disappear with the increasing strain rate[5].If the strain rate is very high,the particle will be shattered to very fine fragments [15].To the best of the author’s knowledge,no explicit definition of the shattering mechanism is given in the literature.However,it may be physically similar to the failure of brittle solids observed under very high compressive loads that reduce the spall(tensile)and shear strength of brittle materials[20–22].King,on the other hand,defines ‘‘shattering” as repetitive breakage (rebreakage) events of daughter (progeny) fragments until all the available strain energy is consumed [23].However,the available strain energy may be insufficient to re-break too many daughter fragments that even become stronger than the parent particle.For example,the experimental findings of Camalan & Hosten suggest that clinker particles may yield a limiting progeny size distribution because of the particle-bed conditions emerging at excess specific impact energies (>12 J/g) [17].Also,there is a powerful empirical function,called Ecs-t10 model,which can well describe the correlation between impact energy and progeny fineness[24].This function predicts a limiting progeny fineness at excess impact energies,indicating that re-breakage events are unlikely at shattering.On the other hand,there is strong evidence suggesting the presence of re-breakage events at secondary cracking:The evolution of secondary cracks is related either to (1) the unbalanced stresses in single-particle impact or to (2) the continued loading on lunar-shaped fragments [5,9,10,13].In fact,rebreakage is likely to occur at low strain-rates on few fragments whose strength is comparable to the strength of the parent particle.

All the above evidence on the breakage modes (from meridian cracks to oblique/radial cracks and shattering)supports the formation of two different progeny populations originating from compressive and tensile stress waves:The compressive waves initially propagate in a much smaller volume (cone of fines) than tensile waves at low inputs of breakage energy.Then,the relative volume fragmented by the compressive waves will enlarge with increasing breakage energy.Eventually,all the volume should be fragmented by the compressive stress waves at the shattering stage.So,it is likely that the progeny size distribution will evolve from a mixture of two distributions of the compressive and tensile failures to a single distribution of compressive failure.Papadopoulos,for example,showed the occurrence of such a transformation for the impact breakage of polymethyl methacrylate(PMMA) particles such that the distribution plot became linear on the log–log scale when the strain rate increased[6].Some literature studies also provide supporting evidence for the distinct progeny distributions generated by compressive/shear and tensile stresses at breakage.Santurbano,for example,showed that the progeny size distributions of impacted limestone particles were well fitted to the sum of the power functions of two different progeny families[14].These families were(1)the cone of fines generated by compression-induced shear and tension at the impact zone,and (2) the coarse fragments generated by tension.Wu showed that the compression-induced shear and tension waves originated at the impact breakage of plaster particles resulted in the generation of finer and coarser progenies,respectively [25].The glass compression tests by Gilvarry&Bergstrom demonstrated the generation of fine fragments under the contact zone and the remainder coarse lune-shaped fragments,which yielded nonlinear size distributions at the log–log scale [26].Grady & Kipp observed that the compression of fused silica resulted in intense fragmentation at the contact zone coupled with the diverging fracture rays [27].Their study concluded that the overall progeny size distribution could be well fitted to a bilinear exponential distribution (Poisson mixture) as a sum of two exponential distributions.

This paper aims to find supporting evidence for the common breakage modes in impact breakage and ball milling,which result from the compressive and tensile stresses at the instant of breakage.For the purpose of this study,single particle impact tests were performed on different size fractions of a cement clinker and a chromite sample at different specific energies.Batch ball mill grinding tests were conducted on the narrow size fractions of cement clinker only.The progeny products of each test were dryscreened with a series of sieves in2-order.Then,the weights in the screen intervals were further measured to obtain progeny size distributions and breakage probabilities for evaluation.The breakage probability (BP) for a narrow size fraction is defined as the cumulative mass fraction of that size class passed to the finer sieves after breakage [28–34].

2.Experimental and material

2.1.Materials tested

Narrow size fractions of a Portland cement clinker and a chromite sample were used as the experimental materials.The size fractions of both samples coarser than 3.35 mm were used in the single-particle impact loading tests.Ball mill grinding tests were performed with the narrow size fractions of the clinker sample finer than 2.36 mm.

2.2.Test work

2.2.1.Impact loading tests

Each drop-weight test was conducted by dropping a steel weight to sample particles one by one.The generated impact energy was equal to the potential energy loss by complete fall of the steel weight,assuming no frictional losses.Then,the specific impact energy applied to sample particles was estimated through the following equation.

where Esis the specific impact energy in J/g(i.e.energy applied per unit mass of sample particles); M the mass of the steel drop-head in kg;h0the drop-height measured from the anvil to the bottom of the steel weight in m; and ˙m the average mass of a particle in the sample in g.There was also an offset height (hf) from the anvil to the bottom of the steel weight after impact.Before each drop-weight test,a few single particle breakage tests were conducted to estimate an average value for hf.When the estimated hfwas comparable to its corresponding h0value,the former term was added to the latter in Eq.(1) to reach a closer input value for the desired specific energy.

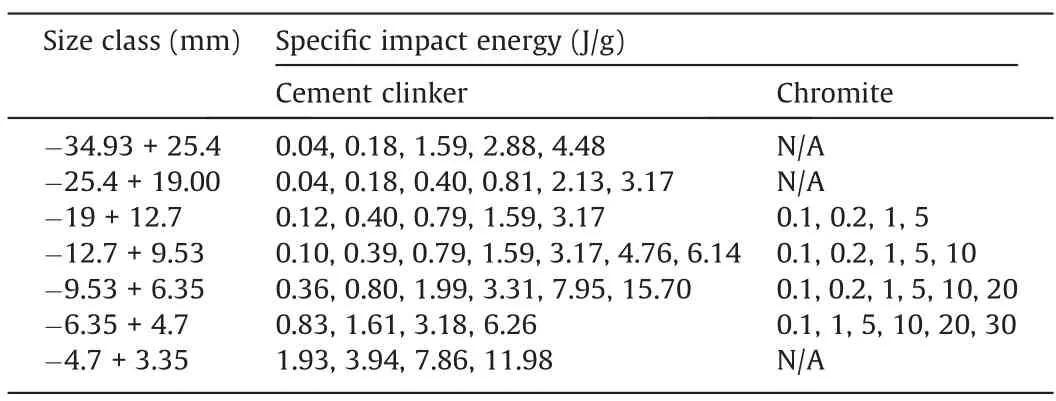
Table 1Specific impact energy levels for the narrow-size fractions of the cement clinker and chromite ore samples.

Impact loading tests were performed with a drop-weight tester on seven size fractions of the Portland cement clinker,and four size fractions of the chromite ore.Four drop-weights (0.4,1,2,and 20 kg) were used with a range of drop-heights (0.03–1 m) to generate a wide range of specific impact energy for each size fraction.The specific impact energies applied to each size fraction are given in Table 1.The product size distributions were obtained by dry sieving using a Retsch AS200 sieve shaker.

2.2.2.Grinding tests

Grinding tests were conducted on four size fractions of cement clinker (–2.36+1.7,–1.7+1.18,-1.18+0.85,and -0.85+0.60 m m)in a batch ball mill having 18.8 cm inner diameter and 17.7 cm length.Approximately 35%of the mill volume,including the interstices within the ball bed,was loaded with 25.4 mm steel balls weighing 8 kg.Each grinding test was performed with 0.63 kg of the chromite ore or clinker for various grinding times from 0.25 min up to 16 min.Mill product size distributions were obtained by dry sieving.

3.Results and discussion

3.1.Evaluating the impact breakage modes through progeny size distributions

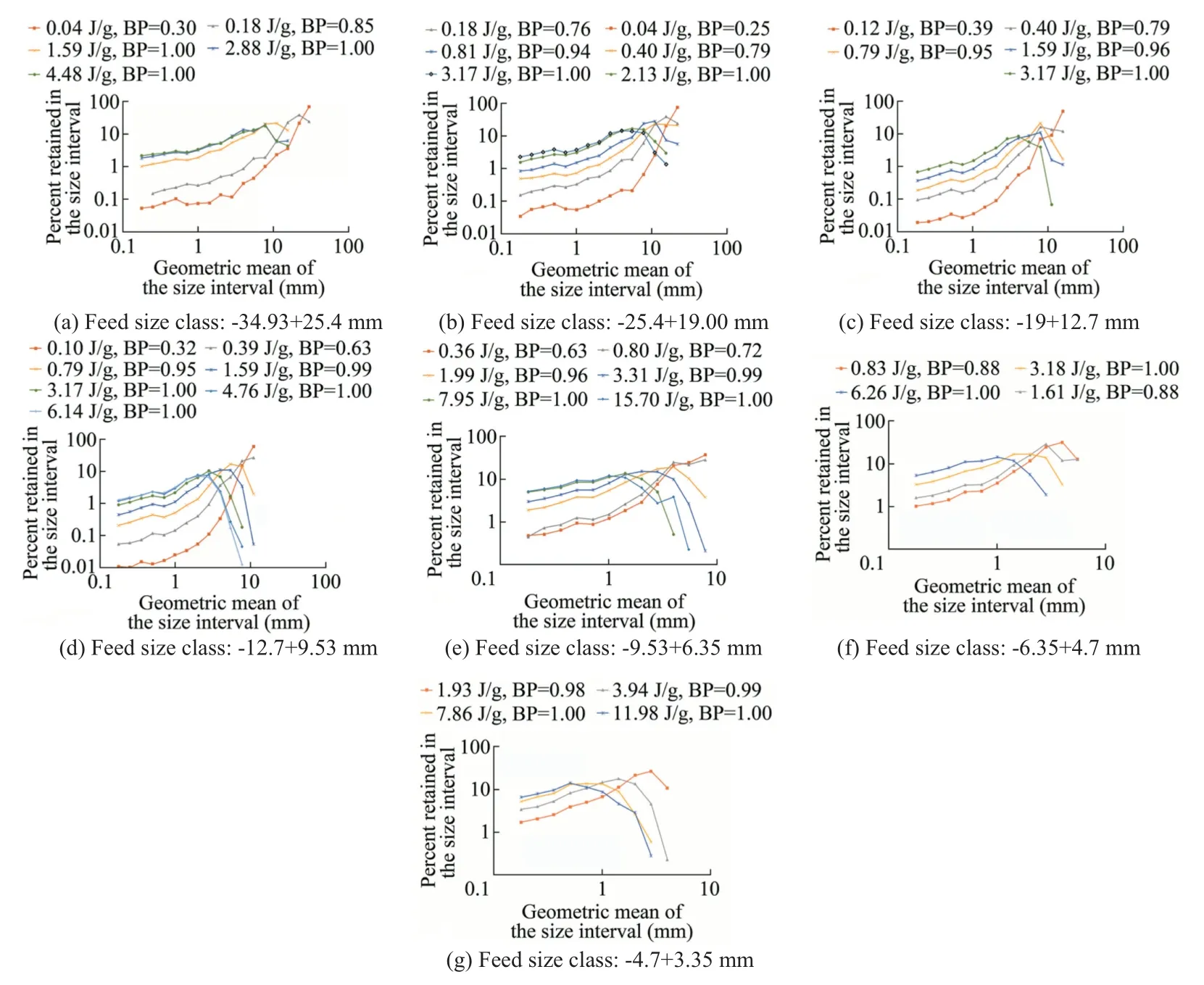
Fig.2.Discrete progeny size distributions of the narrow-size fractions of the cement clinker broken at different specific impact energies (BP=breakage probability).

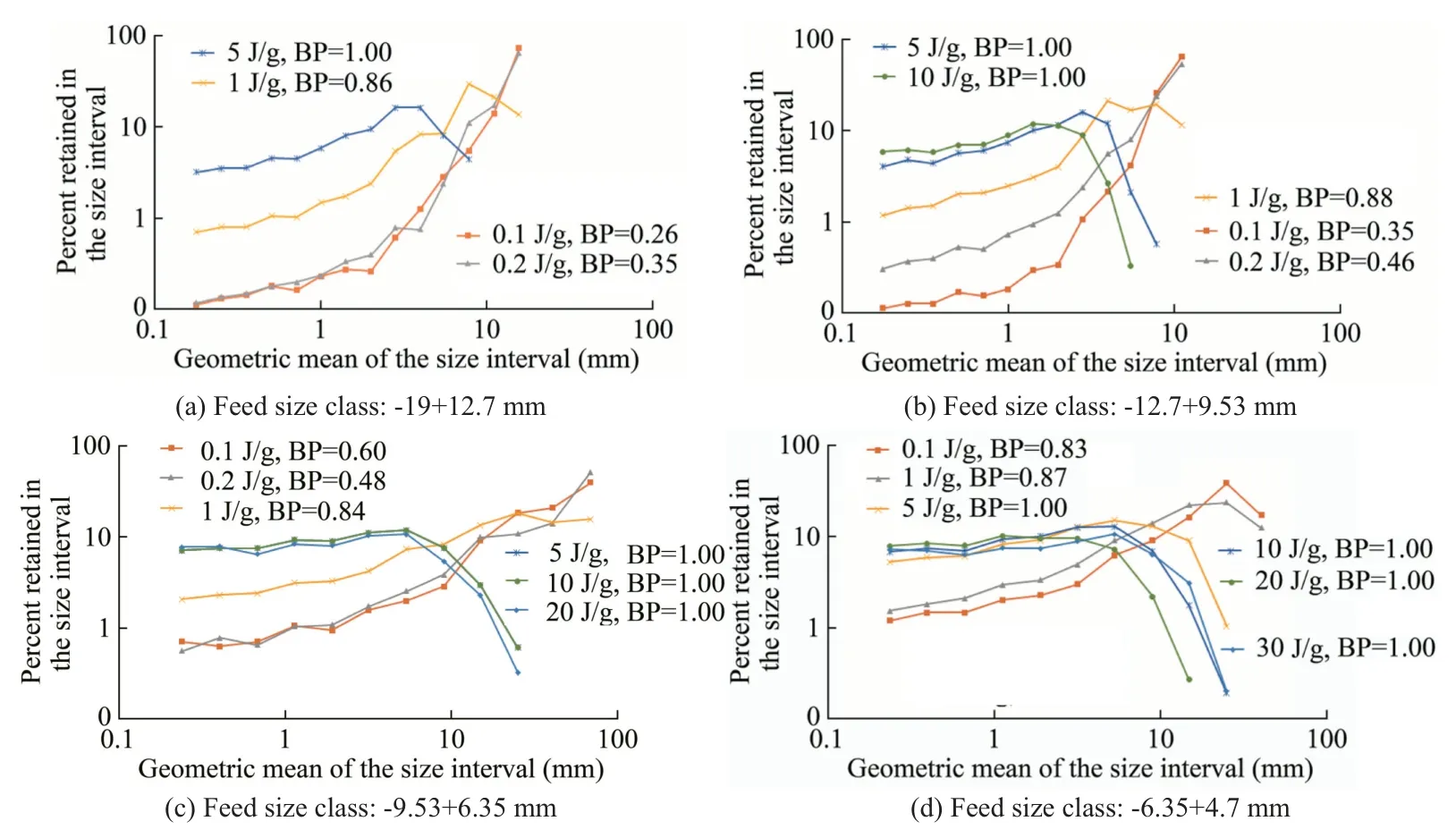
Fig.3.Discrete size distributions of the narrow-size fractions of the chromite ore broken at different specific impact energies.

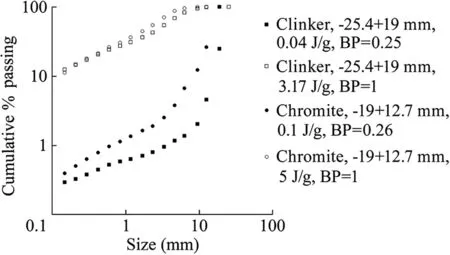
Fig.4.Cumulative progeny size distributions of some narrow-size fractions of cement clinker and chromite ore broken at the lowest and highest impact energies.

Fig.5.Extraction of the size distribution of the cone of fines from an overall progeny distribution obtained at a low breakage probability.

Figs.2 and 3 show the progeny size distributions after impact loading of the size fractions of cement clinker and chromite ore,respectively,at different specific energies.Figs.2 and 3 suggest two distinct peaks that appear at the fine and coarse ends of the size scale (x-axis) but behave differently with increasing specific energy.The major peak at the coarse end of the scale approaches to finer sizes by becoming shorter and wider.However,the peak at the fine end of the scale grows constantly without changing its position.

As discussed in Section 3.1,progeny particles originated at the lowest breakage mode will be the mixture of the cone of fines and the fragments of meridian cracking (Fig.1b) in which the former will occupy a significantly smaller volume than the latter.Therefore,the minute peak at the fine end of the size scale should represent the cone of fines.As the specific impact energy increases,the intensified compressive stresses will expand the cone of fines[9,10,35–37].This explains why the minute peak grows constantly at the fine-scale(Figs.2 and 3).On the other hand,the large narrow peak that appears at the coarse size scale should represent the fragments of meridian cracking that are comparable to each other in size.The increasing impact energy should cause the sequential formation of secondary and oblique/radial cracking that can generate more progeny particles with a wider distribution [16].Therefore,the peak at the coarse-scale (Figs.2 and 3) shifts to the finer sizes and becomes wider with increasing specific energy.Furthermore,this peak seems to shift to the finer sizes more slowly at excessive specific energies.The current author suspects that the slow-shifting peak may represent the large coherent cone given that this fragment cannot disappear easily with the increasing strain-rate [5].The presence of the cone of fines can be seen through the overall cumulative progeny distributions after low breakage probabilities (Fig.4).Fig.4 suggests that the progeny size distribution of chromite or clinker is initially a sum of two linear plots on the log–log scale[6].However,the corresponding plot will evolve into a linear shape with increasing specific energy.The expansion of the cone of fines indicates that compressive stress waves propagate more inside the particle as the specific energy increases.This brings out the question if shattering or catastrophic failure is dominated by the compressive waves.If this is correct,the size distribution of shattered fragments should be similar to the size distribution of the cone of fines.To further test this hypothesis,the size distribution of the cone of fines of the desired size fraction was extracted at the lowest specific energy.Then,the estimated distribution of the cone of fines was compared with the size distribution obtained at the highest specific energy,which was most likely to yield shattering.The approximate size distribution of the cone of fines was obtained from the desired progeny distribution at low breakage probabilities(0.25–0.35),by recalculating the size spectra of the progeny particles below the cut-off point(Fig.5).Then,these plots were fitted to the well-known Gates-Gaudin-Schumann (GGS) equation [38],by using Minitab’s linear regression tool on transformed variables.The corresponding GGS equation is provided below.

Table 2The GGS slopes and their confidence intervals estimated for(1)the cone of fines and(2)the shattered particles after the impact breakage of some size fractions of chromite and clinker.

where Y is the mass smaller than the screen size x,in %; k the top size of the material; and n the distribution slope.As shown in Table 2,the distribution slopes of the cone of fines and the shattered fragments are comparable for each size class.This suggests that compressive failure developed and propagated from the impact zone is largely responsible for shattering.Table 2 also contains 95% confidence intervals of the slopes of the cone of fines and the shattered fragments of each size class.The confidence intervals of the slopes of each size class overlap to a certain degree,suggesting that the slopes of the cone of fines and shattered fragments cannot be different.

3.2.Evaluating the impact breakage modes through normalized cumulative distributions

The abovementioned results support the view that the particles,regardless of their size and composition,pass through the same sequential modes of breakage as the impact energy increases.A graphical way for the detection of similar breakage modes could be obtained by plotting the cumulative progeny distributions on a reduced size scale with respect to the median of the progeny distribution,termed as d50[39].If a set of normalized curves fall onto a single curve or a narrow band,then the corresponding progeny distributions should originate from similar breakage patterns.When the normalized progeny distributions of the clinker and the chromite ore are plotted in groups of similar breakage probabilities(Fig.6),self-similar distributions are obtained except if the breakage probability is equal to one.Despite the lack of evidence,non-self-similar distributions occurring after the complete failure(at the breakage probability of one) may largely correspond to the shattering events at excessive energy levels.Therefore,these non-self-similar curves indicate that excessive impact may shatter the chromite ore and the clinker particles differently.

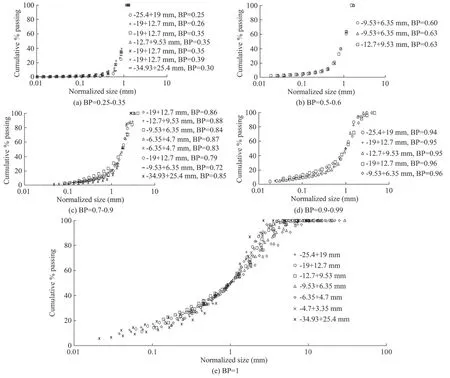
Fig.6.Normalized cumulative progeny distributions of clinker and chromite ore regrouped into similar breakage probabilities.

3.3.Correlating the progeny size distributions after impact breakage and ball milling

As discussed in Section 3.1,all types of steel ball-particle collisions in ball milling (impact,abrasion and chipping) should either mimic the low-or high-impulse impact.Therefore,the impact breakage modes (Section 3.1)are likely to occur at ball mill grinding.It is not easy to assess these modes from the progeny size distributions if the impact events break the parent and progeny particles chaotically.However,this is avoided at short grinding times such that the steel balls are forced to make a few impacts on the parent particles.Therefore,the short grinding activity may be equivalent to a group of drop-weight tests applied to the parent particles.If the normalized size distributions of the grinding products are drawn with the normalized plots of the drop-weight products (Fig.7),a self-similarity between ball mill and impact breakage products can be achieved at a breakage probability range of 0.25–0.4.This suggests that the dominant breakage mode at short-time grinding is meridian/secondary cracking.Then,the non-linear progeny distributions after short-time grinding should represent the mixture of the cone of fines and the fragments generated by tensile failure (Section 3.1).Furthermore,it is hypothesized that the dominant breakage mode in prolonged grinding should be the same as the formation of the cone of fines observed at short-time grinding.This hypothesis was justified through the experimental approach in Section 3.1:The size distribution of the cone of fines was separated from the overall distribution of the short-time (0.25 min) grinding product.Then,the distribution slope of the cone of fines was compared with the distribution slope of the prolonged (16 min) grinding product.Results show that the distribution slopes of the cone of fines and prolonged grinding are similar for each feed size fraction (Table 3),suggesting that the expansion of the cone of fines (shattering) is dominant in prolonged grinding.Also,Table 3 contains 95% confidence intervals for the slopes of the cone of fines and the shattered fragments of each feed size fraction,which are overlapping to a certain degree.Therefore,the slopes of the cone of the fines and shattered fragments cannot be significantly different.

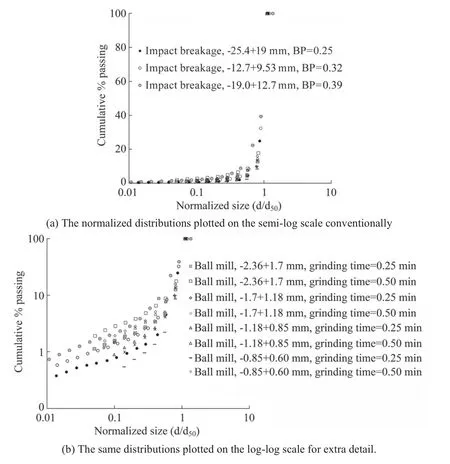
Fig.7.Normalized progeny size distributions of cement clinker after impact loading at low breakage probabilities and short-time ball milling.

Table 3The GGS slopes and their confidence intervals for (1) the cone of fines at short-time grinding and (2) the product at prolonged grinding of cement clinker samples.

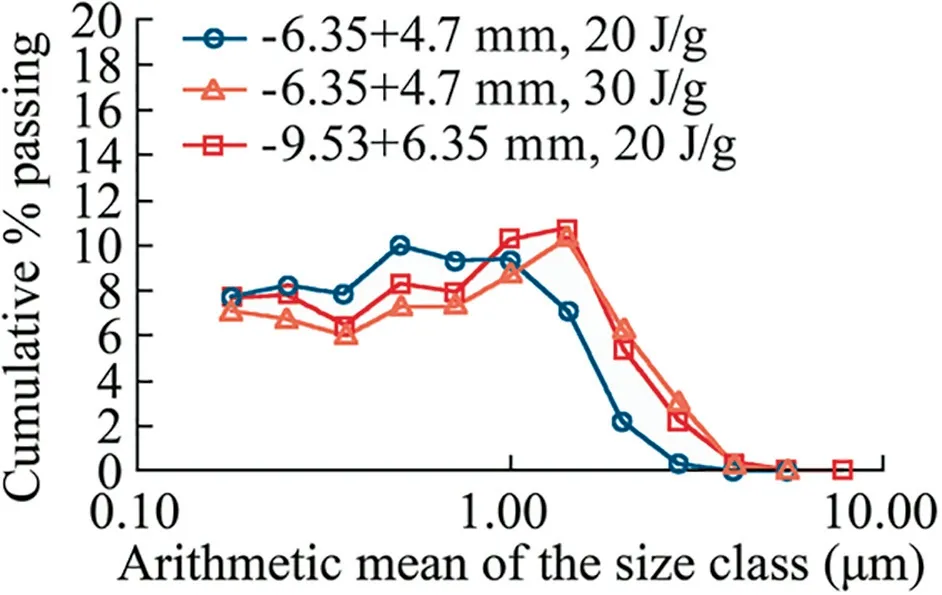
Fig.8.The discrete progeny size distribution of chromite particles broken at specific impact energies higher than or equal to 20 kJ/kg.

The abovementioned results clearly show the formation of meridian/secondary cracking and the cone of fines in ball milling.Besides,these results suggest a transition from meridian/secondary cracking to shattering with increasing grinding time.Therefore,the author concludes that the impact breakage modes(Section 3.1) should occur at ball milling.These breakage modes will ensure that the breakage is governed by (1) tensile stresses at short-time grinding and (2) compressive stresses at prolonged grinding.

3.4.Further remarks on shattering mechanism

The results of this study suggest that shattering should be dominated by the expansion of the cone of fines at excess degrees of breakage energy.Then,the underlying reason for shattering should be the same as the reason that causes the cone of fines.Some studies provide insights into the formation of the cone of fines.Ma et al.,for example,used a combined approach of DEM,FEM,and a cohesive crack model to describe the fracture modes in a single-sided impact [40].Their study concluded that the cone of fines occurs by the propagation of ring cracks to the contact zone.Schönert stated that the formation of the cone of fines resembles the material flow in an ideal-plastic infinite semi-space by a strip load,resulting in the indentation of a cone-shaped section[8].Santurbano discussed that the cone of fines might be formed by a high deviatoric stress field under the contact zone that could be predicted from the Hertz theory of contact [14,41,42].The results of all these studies can be used to assess the underlying reason for shattering.

As introduced in Section 3.1,the experimental findings of Camalan & Hosten suggested that the progeny size distributions of clinker particles approach a limiting shape when the parent particles are stressed with excess impact energies(>12 kJ/kg)[17].The current author is interested if there is a similar threshold impact energy level for chromite particles.As shown in Fig.8,chromite particles may yield a limiting progeny distribution if they are broken at specific impact energies higher than or equal to 20 J/g.

4.Conclusions and recommendations

The impact breakage of brittle materials and rocks resulted in a successive series of breakage modes (from meridian/cracking to oblique/radial cracking to shattering).This study investigated whether these modes are common at impact breakage and ball milling of clinker and chromite samples.Results show that the corresponding impact breakage modes occur at impact breakage and ball milling of the two samples.Further studies should be conducted to assess if these impact breakage modes occur at the size-reduction of different ore types.

The results suggest that the breakage of clinker and chromite samples is dominated by tensile stresses at low breakage energies and compressive stresses at high breakage energies.The underlying reason for shattering should be the same as the reason for the formation of the cone of fines.Non-self-similar size distribution curves indicate that shattering patterns may depend on the particle composition.However,the other breakage modes (meridian/secondary and oblique/radial cracking) produce similar breakage patterns for the clinker and chromite samples.