基于基本活动经验的教学设计研究
——以“双曲线的渐近线方程”为例
2020-12-17王思俭江苏省苏州中学215007
王思俭 (江苏省苏州中学 215007)
1 问题提出
1.1 现状分析
笔者近两年就“双曲线的几何性质——渐近线方程”的教学情况进行了调研,先后随堂听课36节.其中,只有一位教师从具体的双曲线方程利用几何画板演示渐近线的形成,再进行例题讲解;12位教师将此性质并入其他几何性质,并且带领学生阅读课本内容,然后进行反复强化训练;23位教师直接将双曲线的渐近线方程告诉学生,再结合其他性质做一系列的综合题.不但没有系统讲解知识的形成过程,而且没有具体的课时安排,而是与其他知识混搭,更没有立足学生已有的基本活动经验去进行教学设计,仍然是关注题海战术,有的一节课讲解25~30个题目,学生机械模仿,没有自己的思想,更没有思考与交流的机会.
新一轮课程改革的宗旨是让学生学会思考,进而学会终身学习.鉴于此,笔者受苏州大学数学科学院的邀请,于2019年11月15日为2016级本科生和2017级研究生以及苏州中学数学组青年教师执教了“双曲线的渐近线方程”,旨在希望他们将来在自己的教学实践中要关注学生的学习、交流和思考,提高学生的思维能力和学科素养.
1.2 教材分析
双曲线的渐近线方程是其几何性质之一,苏教版高中数学教材选修2-1第41页详细阐述了渐近线方程的由来,并从极限思想出发作了理性说明,但学生仍无法接受这种粗略的描述性说明.能否从学生的基本活动经验出发,利用从特殊到一般的数学思维方法,寻求新的教学思路?
1.3 学情分析
教学对象是本校高二15班31名学生,该班是本校与中国科学技术大学联合创办的首届少预班,学生是从初二直接选拔读高中的,年龄都是15~16岁.他们思维活跃,反应较快,接受能力、自学能力和理解能力较强,但数学书写往往不到位,特别是逻辑推理方面欠缺.选择这节内容开设公开课,旨在引导学生会用数学语言表述事件.
2 教学实录
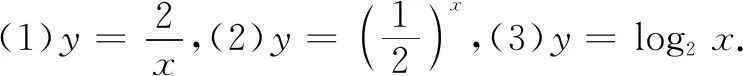
师:第(1)个函数的图象叫做什么?在第一象限内随着x趋近正无穷,函数图象变化如何?
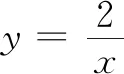
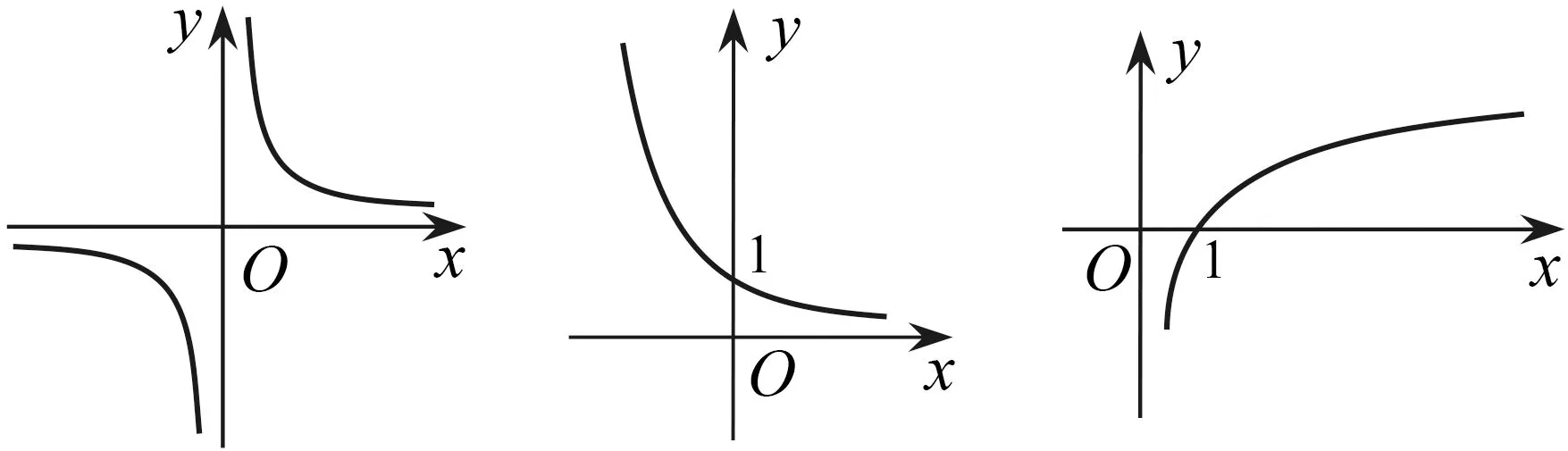
图1 图2 图3
师:正确!这时我们把x轴、y轴叫做它的渐近线.后两个函数的图象情况怎样?
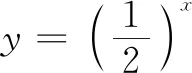
生3:函数y=log2x的图象随着x无限趋近于0+,图象无限接近y轴,但不能越过y轴(图3).
师:很好!你们从直观想象层面上理解渐近线,那么你们能从逻辑推理层面再给出解释吗?
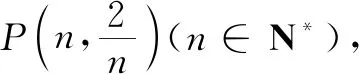
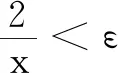
师:很好!你能找出x0吗?
师:非常好!生6从离散量到连续的量进行严格推理证明,对于后两个函数图象的渐近线又如何推理研究呢?
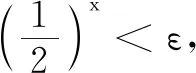
师:很好!
设计意图基本活动经验1——初等函数从图象上研究曲线的形状、特征,从几何直观上理解渐近线,体现直观想象核心素养,再从数据分析上理解渐近线.
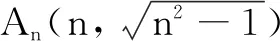

An(1,0)(2,3)(3,22)…(n,n2-1)…dn

设计意图基本活动经验2——利用点到直线距离公式,体现数据分析核心素养.
师:正确!请研究点An满足的规律是什么?
生10:点An在曲线x2-y2=1(x>0,y>0)上,即双曲线的第一象限内的一部分.
师:请作出点An所在曲线的图形及直线y=x的图形.
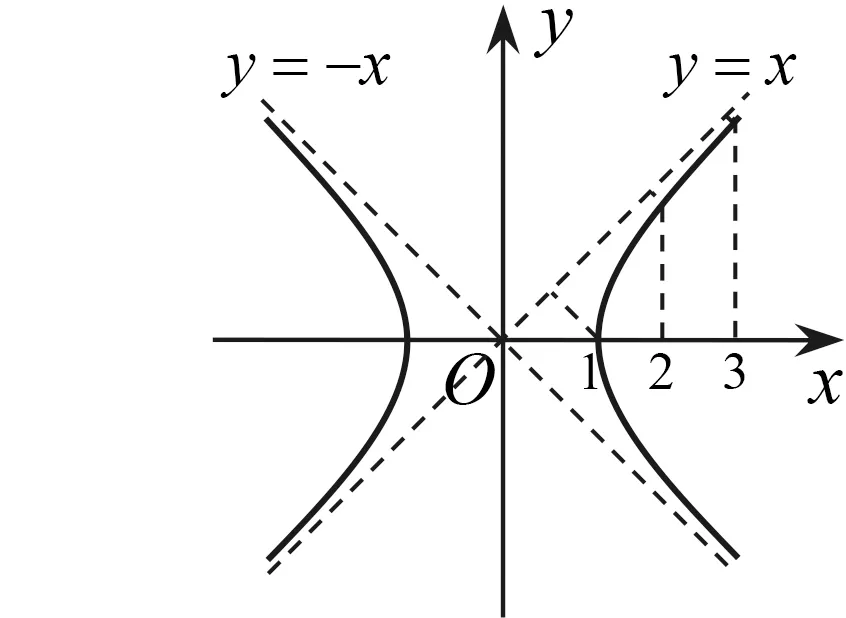
图4
生众:(在自己座位上画图,教师走到学生中间巡视)利用对称性可以拓展得到曲线x2-y2=1与y=±x的图形.
师:当n趋近正无穷,dn的变化趋势如何?
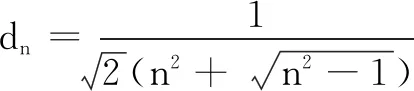
生众:不严谨,需要证明.
师:哪位同学来证明?
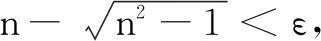
生13:这里n应该是任意正实数x,当x→+∞时,d→0.
师:非常好!你们从哪里学到的?
生13:我在高等数学书上看到的,自学了一点,这样讨论我更加清楚了.
师:通过证明,运用类比思想,把直线y=±x叫做双曲线x2-y2=1的渐近线.
设计意图体现数据分析、逻辑推理、数学运算、数学抽象等核心素养.
生众:能否将上述问题推广?
师:很好!请填写下表(点An到直线l:bx-ay=0(a>0,b>0)的距离dn),并回答问题:

An(a,0)(2a,3b)(3a,22b)…(na,n2-1b)…dn
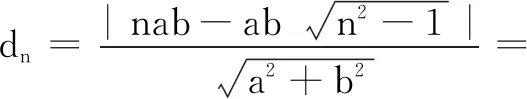
问题1 观察An的特征.(或所在曲线是什么?)
问题2 观察点An到直线l距离dn的特征.
问题3 你能发现什么规律?
与国内的工作环境相比 ,境外工作将面对的是一个完全不同的工作环境 (其中包括社会、政治、经济、法律、风俗习惯、地理气候、施工工艺等方面),所以对所有参与海外项目的工作人员提出了高标准、高水平、高素质的严格要求。
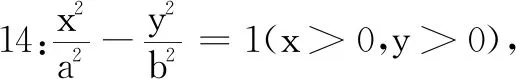
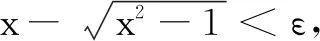
师:很好!实质就是刚才的特例.
问题4 你能改进计算距离的算法吗?
设计意图培养学生从特殊到一般的思维方法,训练数学抽象、逻辑推理等核心素养.
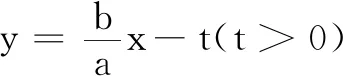
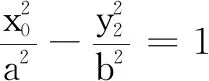
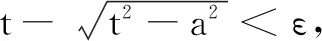
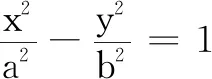
生21:如同椭圆对应矩形MNPQ(其中M(a,b),N(-a,b),P(-a,-b),Q(a,-b))的两条对角线.
师:这也是作双曲线图象草图时常用的方法,生21是利用类比的方法得出,很好!
师:这种记忆方法与双曲线方程形成统一美、对称美、和谐美,数学之美无处不在!请你们探究——渐近线的斜率与离心率的关系是什么?
设计意图利用类比思想研究双曲线的几何性质,训练学生的数学抽象、直观想象能力,让学生发现并欣赏数学的美,传播数学文化.
师:很好!同学们也总结出双曲线渐近线方程两种不同的记忆方法,反映出同学们有较强的直观想象、类比推理和逻辑推理能力.希望大家继续努力,要有探索和创新的精神!现在看两道小题(略).
3 教学反思
教师是教学的主导.主导在很大程度上可以理解为教学导向,即在教学过程中进行启发、暗示、引导.在新课标的核心素养导向下,教师的主导地位体现在:提供学习的方向和目标、提供交流的情景和机会、提供思考的问题和动力,即学生能做的就让学生做,教师把握一个大的方向.正如杜威所说:“他掌着舵,学生们用力把船划向前去.”[1]
教学反思是教师进行教学活动的重要思维活动,是教师发展的重要途径,也是课堂教学的原动力.因此,教师应该努力对每节课进行教学反思,以提升自己的专业素养.
3.1 教学生学会学习
要使学生获得可持续发展,还要让学生学会学习,教给他们学习的方法,使他们学会独立地获取知识;学会研究问题的方法,学会从不知开始,一步一步地达到问题的核心,直至最终的问题得以解决.
自主学习、探究学习是一种学生主动获取知识、发展能力的学习方式.[2]新课标强调学生要学会学习,倡导学生在经历新知识的产生过程中获取科学研究的一般方法,提高以后解决新问题的能力.因此,在教学过程中教师要努力为学生创设宽松愉悦的探究氛围、提供平等对话的机会.这样能调动学生个人经验的参与,激发学生丰富的想象力,加深对知识的理解.
3.2 教学生学会交流
“数学是思维的科学,数学教学是思维的教学.”[3]在课堂教学过程中,及时追问是提高学生思维参与、加速知识领悟的重要策略.面对学生简单短小的回答,教师需要及时追问,在追问过程中了解学生的理解程度,捕捉可能的问题,补救可能的不足.
对话、沟通、合作、交流已经成为现代教学方法突出的特点.传统教学中教学活动的单向性、师生交流的匮乏对教学效果的不良影响已经逐渐得到重视,课堂越来越被看成是合作、交流的融洽的学术交流场所.概念型课作为合作交流学习的一种方式,如“双曲线的渐近线方程”,给学生提供更多展现自我的机会.因此,在教学中努力暴露学生的思维过程,本节课上教师不满足于学生答对问题,而是通过追问检查学生的思考状况,明确每一个环节的意义,让学生加深对知识的理解.对于教师的追问,学生未必能一次就回答到位,教师应该给予积极的鼓励,增强他们直面挑战并战胜困难的勇气、毅力和信心,给他们创造体验成功的机会.
3.3 教学生学会思考
教学生学思考是数学教学的首要任务,数学教学就是“教会学生去思考”[2],注重科学研究一般方法的渗透是有效教学的必要条件.本课以问题驱动学生思考,在问题情境和问题解决中感悟数学原理,有提出猜想、有制定方案、有实施方案、有概括总结、有反思提升,学生会在这样的教学情境中自然而然地感受了科学研究的过程,实践了科学研究方法.
波利亚曾说过:“令人讨厌的艺术就是把什么都说出来.”[3]新课标提倡学生自主探究、学会思考.这要求教师尊重学生的主体性,提供充分的思考空间,让学生在问题探究中表达自己的想法,修正自己的发现,完善自己的知识结构.本节课上,教师鼓励学生不断探索、完善用数学语言刻画“距离越来越趋近于0”“你是怎么想到的?请把你的想法告诉大家”“想一想,这两种距离哪个更好?”“大家还有什么想法?”这些引导语把学生的积极性调动起来,让学生大胆地说出自己的想法.课堂上学生思维活跃,畅所欲言,成了课堂的真正主人.
