发展直观想象能力 促进初高中教学衔接
2020-12-17庄志红江苏省镇江市教育科学研究中心212008
庄志红 (江苏省镇江市教育科学研究中心 212008)
学科核心素养附着在知识本体上,在问题的解决中显现,但归根结底是直接指向数学的本质,所以说发展学科核心素养不仅不会受到各个学段的知识的限制,而且还将成为实现学段间有效衔接的关键.作为初中教师,我们应立足《义务教育数学课程标准(2011年版)》,着力发展学科核心素养,使之成为学生后续发展的衔接点和推进力.直观想象是指借助几何直观和空间想象感知事物的形态与变化,利用空间形式特别是图形,理解和解决数学问题的素养.[1]本文想谈一谈通过发展学生的直观想象能力促进初高中教学衔接.
1 着力打好“直观养成”的基石
直观想象是《普通高中数学课程标准(实验)》中“空间想象”和《义务教育数学课程标准(2011年版)》中所提及的空间观念、几何直观的融合与凝练,是从几何学的视角——几何直观、空间想象、空间形式、图形等进行的描述,凸显了直观想象的几何特征.在教学时,应当给学生足够的时空进行观察、阅读和数学实验等数学活动,为“直观养成”奠定基石.
1.1 观察现实世界,增强直观感悟
数学来源于现实世界,也是对现实世界的抽象,教学中应借助现实情境和实物等帮助学生理解数学.比如,七年级学习“数轴”时,教学中可呈现一支温度计(图1),使学生能直观感受到用一条带有刻度和“临界点”的直线就可以表示数值,当规定了方向后就抽象出了数轴.同时,也引导学生发现数轴不仅可以水平放置,还可以竖直放置,单支数轴上的点可以表示一个数值,为后续平面直角坐标系以及高中阶段空间直角坐标系的学习打下感性基础.又比如,方程是数学中的天平(图2),是对互为等量关系的一类数学表达;从加油站的仪表盘中能直观看到加入的油量和金额这两个互相依存的变量(图3),函数就是这两个量之间依存关系的一类数学表达.这些情境的创设,旨在培养学生的直观感受,为今后的学习预埋了伏笔.
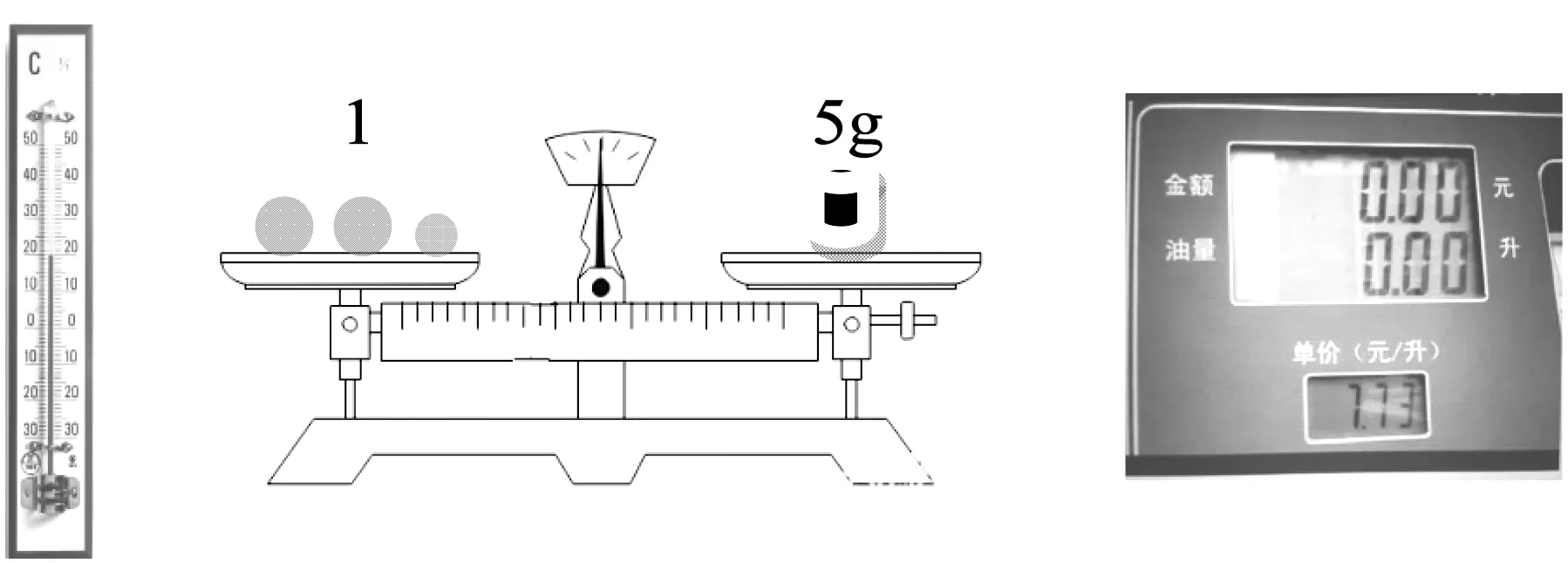
图1 图2 图3
1.2 加强几何作图,培养直观想象
初中学生在学习平面几何时,接触的多是现成的具体图形,这些标准的图形虽直观却也会固化想象.因而适当增加几何作图,有助于学生从运动变化的维度看问题.
例如,在学习了“如果两个三角形全等,那么它们的对应边相等、对应角相等”后,可以设置各种作图任务探索三角形全等的条件.如用三角板作△ABC,使AB=4 cm,∠B=60°,然后请同座位的两位学生对比他们所作的三角形是否全等.学生从作图很直观地发现点C的不确定性带来了不一样的三角形.要保证全班学生作出的三角形都一模一样(也就是三角形是全等的,是唯一确定的),就是要确定C点的位置,很自然地就得到“边角边”“角角边”“角边角”.特别地,点C在运动的过程中还会出现两个特殊的位置(∠C=90°,∠A=90°,图5).再进一步提出问题思考:给定边长AC的取值分别为2 cm,3.5 cm,5 cm,能否作出全等的三角形?
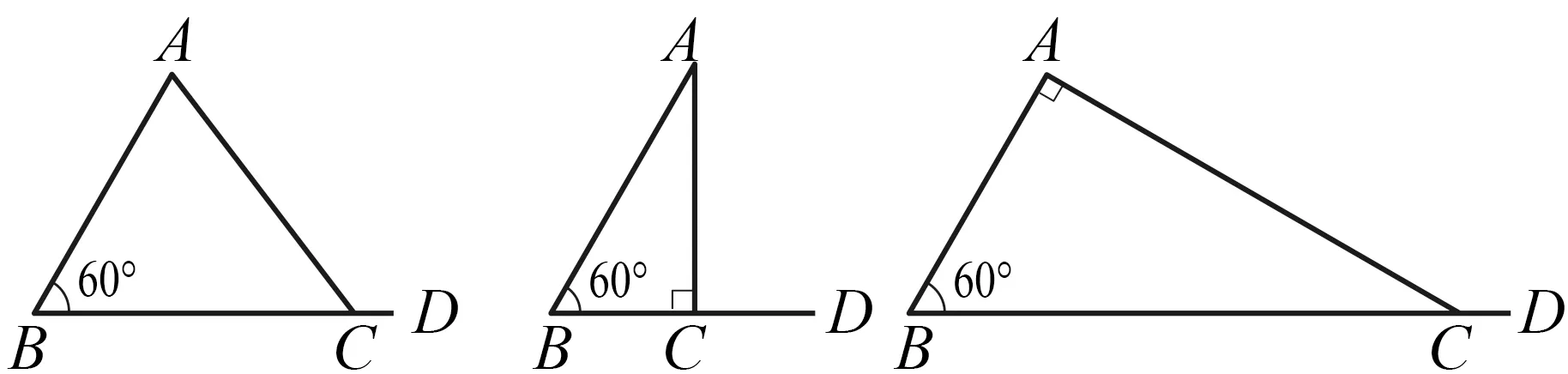
图4 图5
学生通过画图(图6~图8)操作,不难想象并得出:如果两个三角形的两边和其中一边的对角分别对应相等,那么这两个三角形不一定全等.这个“操作性反应”在高中阶段正弦定理的学习中还会自然产生.
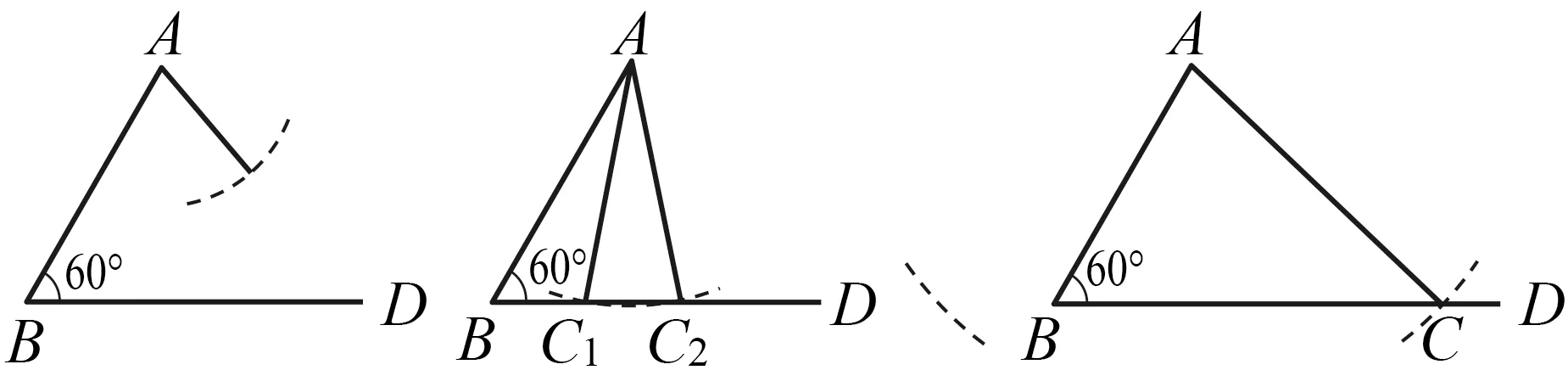
图6 图7 图8
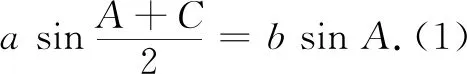
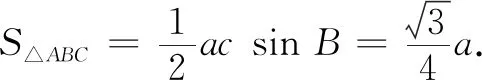
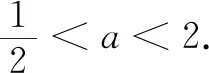
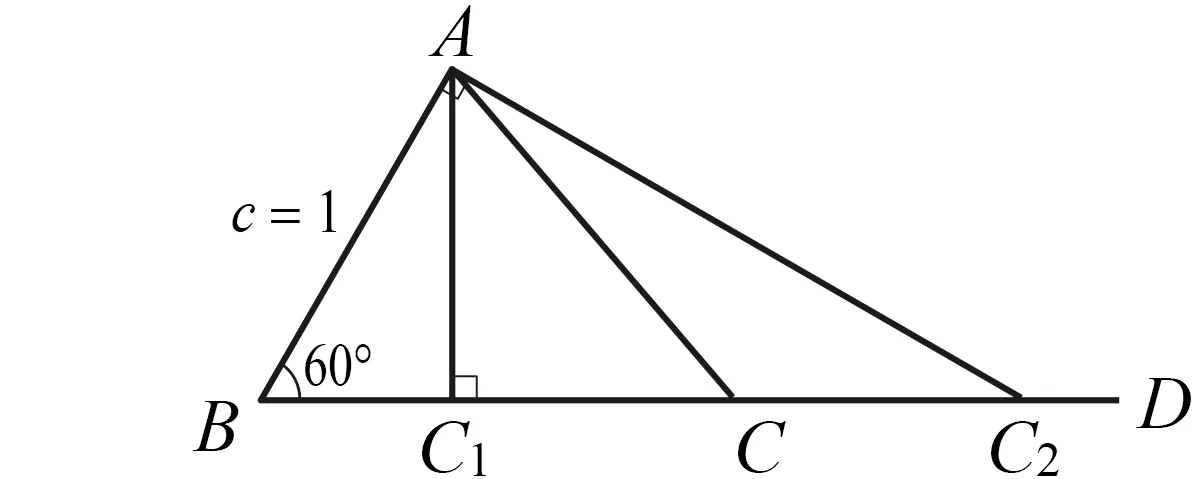
图9
1.3 动手操作实验,发展想象能力
数学实验是通过动手动脑“做”数学的一种数学学习活动,是学生运用有关工具(如纸张、剪刀、模型、测量工具、作图工具以及计算机等),在数学思维活动的参与下进行的一种以人人参与的实际操作作为特征的数学验证或探究活动.[2]从发展学生想象能力的角度看,数学实验有着非常好的“操作性反应”的刺激效果,这是因为当学生在设计或完成一项实验任务时,往往需要在现实与数学中切换思维,一般而言是先有了想象后的结果,再将“思考”转化为“操作”,达到“思行合一”.因此,在初中数学教学中要充分挖掘学科实验的育人价值.
例如,实验主题“拼图”.
操作与思考1 如图10,能否用5张这样的三角形纸片ABC拼成一个内外都是正五边形的图形?
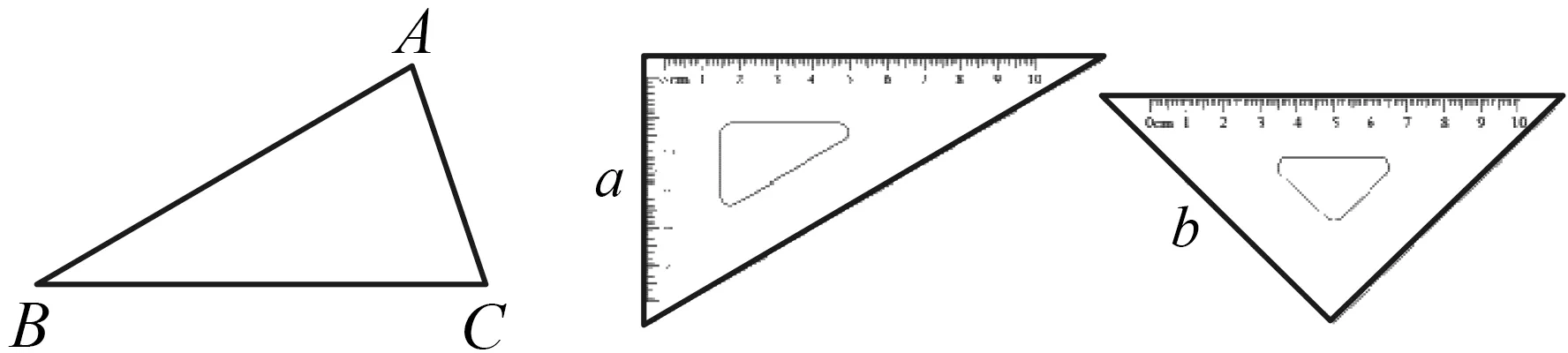
图10 图11
操作与思考2 图11是我们日常熟悉的三角尺,用两副这样的三角尺拼成一个含有75°角的平行四边形.
在活动1中,学生通过想象画出正五边形ABDEF(图12),并根据图形的几何特征得到:只有当三角形纸片的两个内角满足和为108°时,可以拼成正五边形.
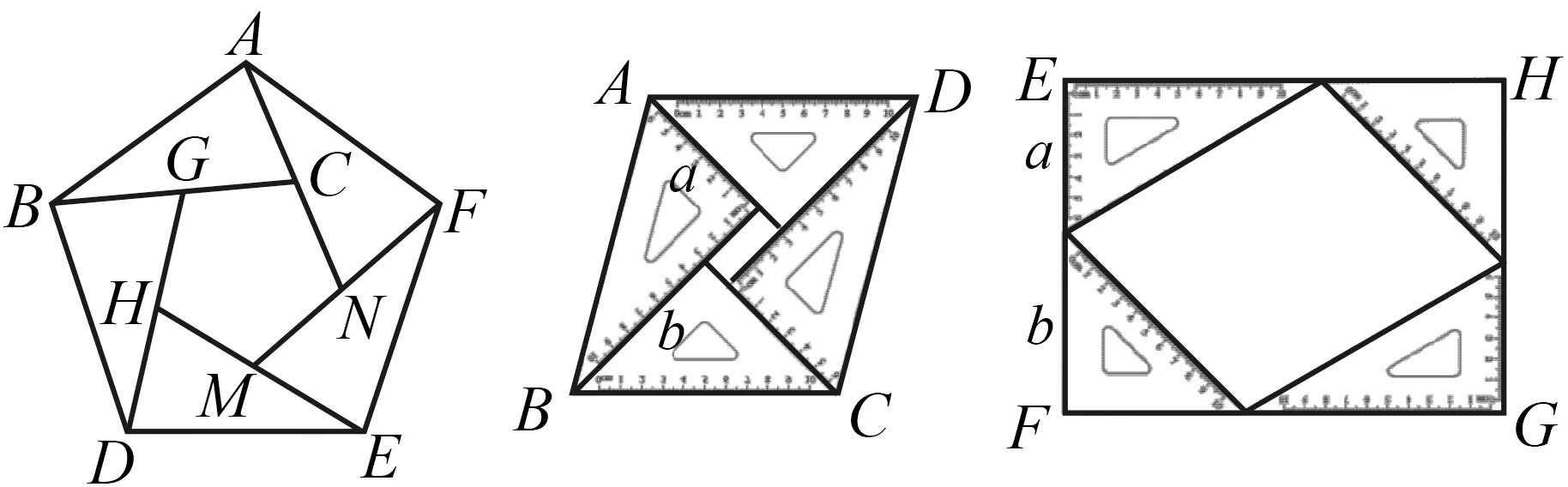
图12 图13
这样的实验操作正是利用了工具的直观性完成对未知结果的想象,并产生新的认识和方法.
2 强化拓展“直观思维”的路径
提升学生的直观想象能力,重要的依托就是几何,也就是图形化的表达方式.借助几何的表达方式,可以直观地进行数学思考与想象,将抽象的概念内涵形象化、具体化,引导学生更好地理解概念,构建知识体系,促进学生从“不自觉”的直观走向“自觉”的直观,从而拓展“直观思维”的路径.
2.1 强化螺旋上升的单向思维能力
螺旋上升不是机械重复的训练,更多的是遵循知识发生发展的逻辑顺序和学生认知水平的发展规律不断提升.例如角是初中阶段最常见的一个基本图形,可以通过对教材进行梳理,形成若干条单向思维的训练主题.
第一次操作是用量角器度量角度,将∠AOB的顶点放在中心位置,一边与0刻度线OC重合(图14),观察到点D与点C在量角器的边缘弧上,帮助学生直观形成了尺规作∠A′O′B′=∠AOB的方法.
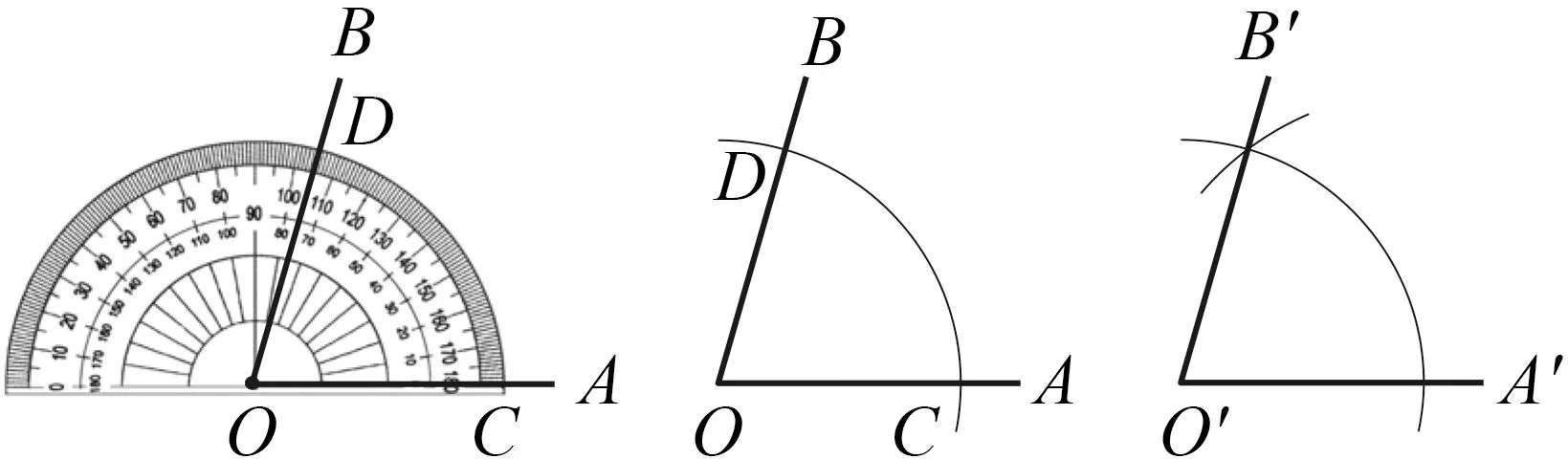
图14
第二次操作可以安排在锐角三角函数的学习中.我们知道函数有两个本质属性:一个变量随另一个变量的确定而确定,随它的变化而变化.此时可借助量角器的直观,随着锐角θ的值增大,tanθ的值随之而增大(图15);同样,利用图16中的量角器,可直观理解锐角的正弦函数和余弦函数.这其中蕴含了三角函数线的雏形(图17).
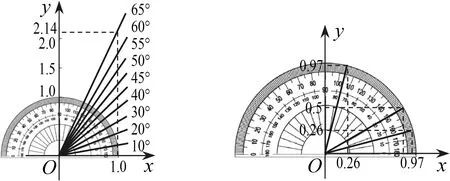
图15 图16
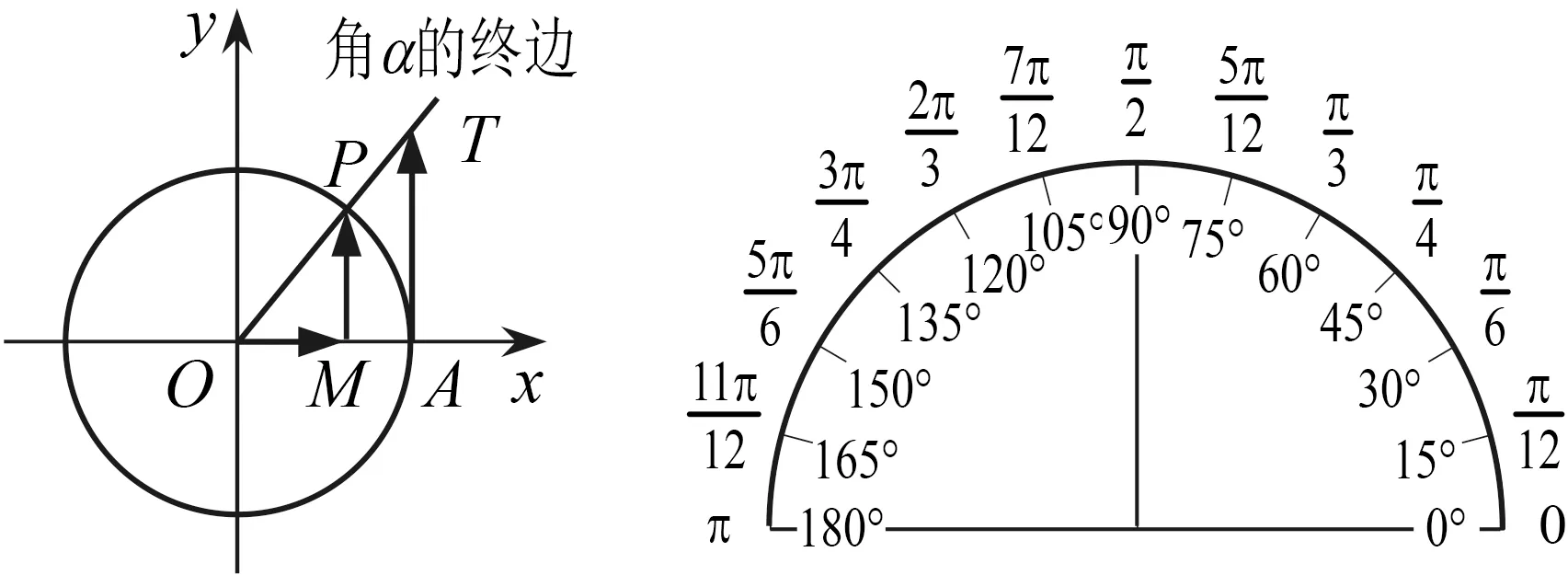
图17 图18
第三次操作是高中阶段学习弧度制时,将量角器的平角(π)十二等分(图18),增强学生对一些特殊角的弧度数与角度数关系的直观感受.
通过对量角器的直观的不断认识和运用,在今后高中相关知识的学习中将量角器抽象为一个单位圆时,对学生而言就会觉得自然亲切、印象深刻.教学中应梳理教材,围绕“主线”逐步强化,促进学生对直观形成深刻的“条件反射”.
2.2 培养数形结合的双向思维能力
数学是研究数量关系和空间形式的科学,因此数学里的直观多来自于数量关系的结构特征或图形的位置特征.对学生不断强化关注数与形的相互转化,形成“由数想形、以形助数”的条件反射.
(1)借助数式的结构特征展开形的想象
学生的数感和符号意识都是操作性反应,因此在学习“数与代数”的主干内容中要不断强化,促进学生自觉地“由数想形”.
学生在初中阶段接触的函数,它们的表达式蕴含了丰富的信息,像二次函数的三种常见的表达式y=ax2+bx+c(a≠0),y=a(x-x1)(x-x2) (a≠0),y=a(x-h)2+k(a≠0)中的数值a,b,c,x1,x2,h,k都有着特定的几何意义,教师应不断提醒学生,做到能根据数量的结构特征想象并画出形的“概貌”,使得研究对象变得直观、具体而全面.例如“抛物线y=ax2+4ax+4a+1(a≠0)过点A(m,3),B(n,3)两点”,这样的语境中含有函数表达式的结构特征,将其转化为y=ax2+4ax+4a+1=a(x+2)2+1,并结合A(m,3),B(n,3)两点纵坐标的数值特征,可以想象并画出抛物线的大致形状(图19).进一步还能从图象的位置特征直观看出线段CD的长为4.一旦有了“形”,这个抛物线的所有性状都变得具体而直观.
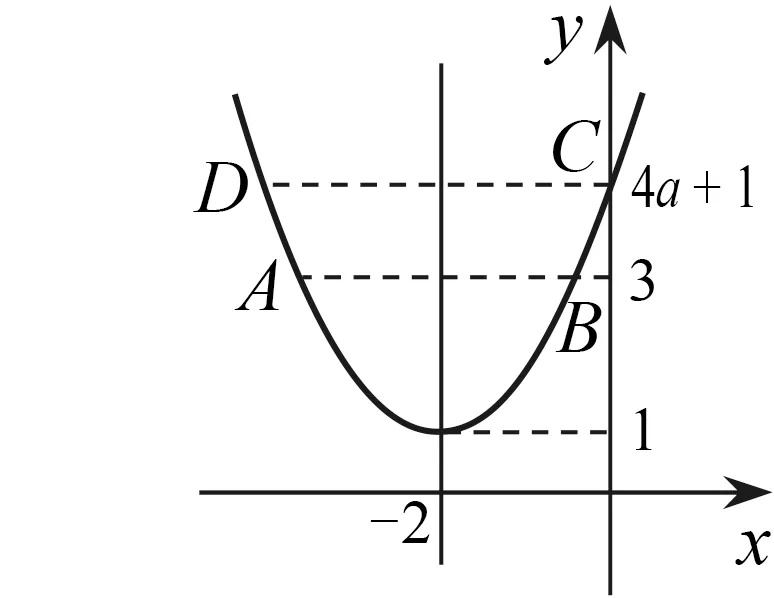
图19
这种“由数想形”的直观思维在问题解决中很常见.如2020年山东卷第10题题干“若定义在R的奇函数f(x)在(-∞,0)上单调递减,且f(2)=0”中,若能根据“数”的语言迅速转化并描绘出函数的大致图象,问题便迎刃而解.
事实上,“数与代数”中的数、式、方程、不等式、函数,原本就是客观世界的抽象和直观表达,教学中应对学生反复强化,发展学生的数感和符号意识,生成“由数想形”的直观思维.
(2)借助图形的直观特征生成数的表达
帮助学生理解算理、掌握算法是培养运算能力的关键.代数中的很多公式和结论并没有通过逻辑推理得到,但是可以借助图形的几何直观帮助理解,体现“以形助数”的价值.
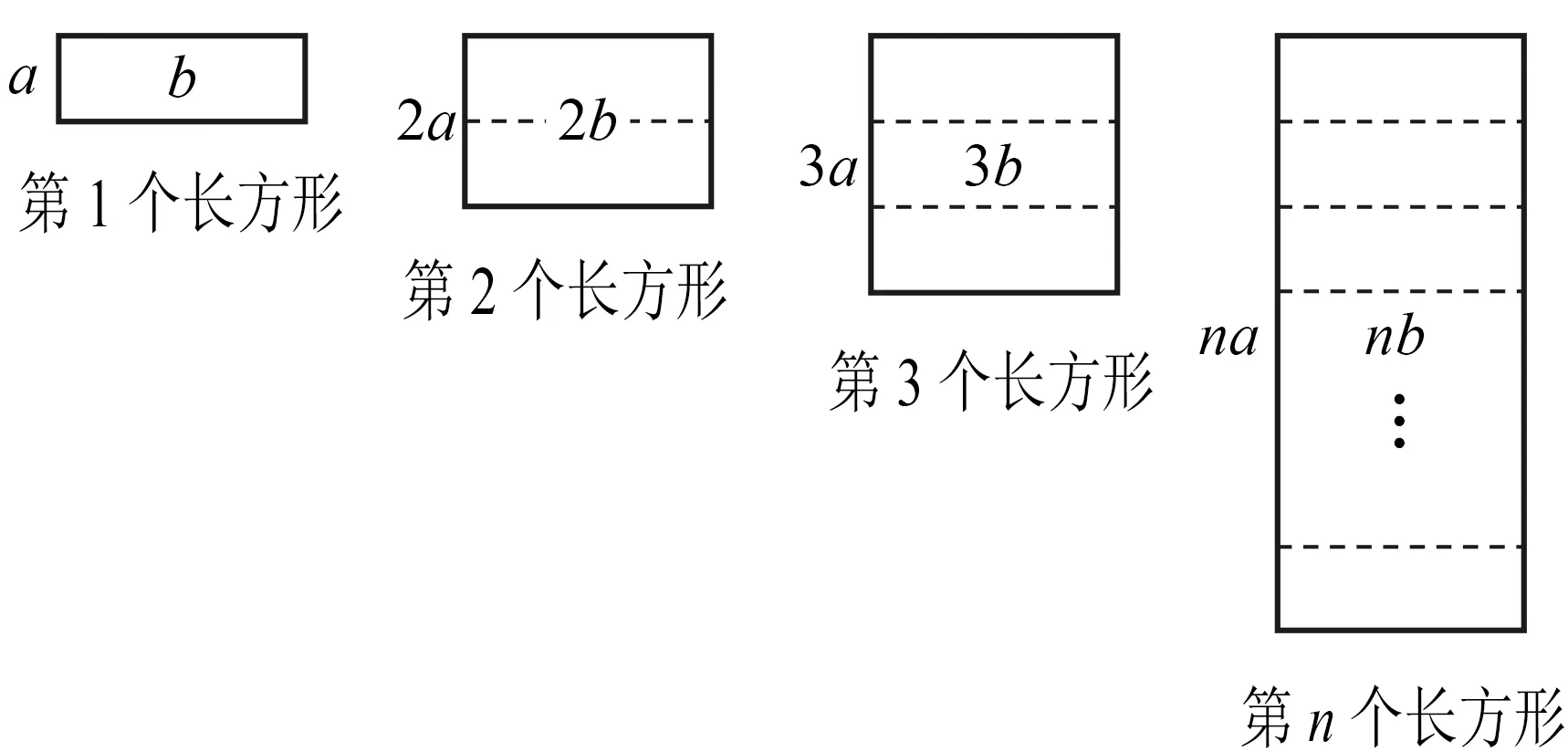
图20
3 结语
初高中的知识模块看似独立,却有着密切的关联性,这种关联归根结底是能力的关联、素养的关联.应让学科素养在我们的教与学中落地生根,焕发出旺盛的生命力,使学习成为一种“有机”的生长.
