素养导向下的高考应用题分析研究及教学建议
2020-12-17江苏省南京市教师培训中心210002
蔡 欣 (江苏省南京市教师培训中心 210002)
文[1]指出,高考正在实现由能力立意向素养导向的历史性转变,所谓素养导向下的高考命题,更注重科学思维的考查,更注重科学探究能力的考查,更注重情境化试题的考查.这些考查无疑都是指向数学核心素养的,更强调分析和解决实际问题的关键能力,更凸显数学的应用意识[2],而考查核心素养和关键能力的较好载体就是应用题.环顾高考数学全国卷和其他省市试卷,大多数应用题都以概率统计知识为背景,而江苏这么多年来都是基于三角、函数(导数)、不等式、数列、立体几何等知识为背景命制应用题,这无疑是江苏卷的一大特色.本文以2019年江苏卷应用题为例,结合2020年新高考I卷应用性试题,分析研究核心素养导向下的高考应用题,并试图给出一些教学策略和建议,以期与同行探讨.
试题如图1,一个湖的边界是圆心为O的圆,湖的一侧有一条直线型公路l,湖上有桥AB(AB是圆O的直径).规划在公路l上选两个点P,Q,并修建两段直线型道路PB,QA.规划要求:线段PB,QA上的所有点到点O的距离均不小于圆O的半径.已知点A,B到直线l的距离分别为AC和BD(C,D为垂足),测得AB=10,AC=6,BD=12(单位:百米).
(1)若道路P1B与桥AB垂直,求道路P1B的长;
(2)在规划要求下,P和Q中能否有一个点选在D处?并说明理由;
(3)在规划要求下,若道路PB和QA的长度均为d(单位:百米),求当d最小时,P,Q两点间的距离.
1 特点分析
本题是一个典型的真实情境化问题,问题背景涉及路桥问题,切合生产实际,贴近学生生活,与苏教版《数学5》(必修)第14页例2有异曲同工之妙,故可认为是教材的改编题,可谓源自教材,背景公平.本题给出配图,图形帮助学生快速读懂题意[3],但没有给数学模型,属于有图无“模”型.
2 策略研究
图2是应用性问题的一般操作流程,可以看到,这是从实际问题原型到数学模型再回到实际问题原型的认识过程,它的核心环节是数学建模.
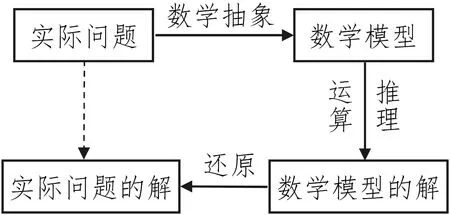
图2
2.1 研读题目
要特别注意本题中“所有点”“不小于”“当d最小时”等关键信息.
2.2 数学建模
对实际问题进行数学抽象,并用数学语言予以表征,构建数学模型(如函数、方程、不等式模型),确定参数,运算求解,对计算结果进行检验,必要时还需改进优化数学模型并再次求解检验,直至解决问题.可以看到,数学建模至少包括三部分——将实际问题抽象为数学问题,确定参数构建数学模型,数学运算求解数学模型.
·数学抽象
数学抽象搭建了数学与外部世界的桥梁,它是数学核心素养之一.这一过程中,需要剥去题中无关解题的背景和表象,保留对象中的数量关系和空间形式.本题的数学表述如下:
如图3,已知AB是圆O的直径,点A,B到圆O外直线l的距离分别为AC和BD(C,D为垂足),其中AB=10,AC=6,BD=12,P,Q两点在直线l上,且PB,QA上的所有点到点O的距离均不小于圆O的半径.
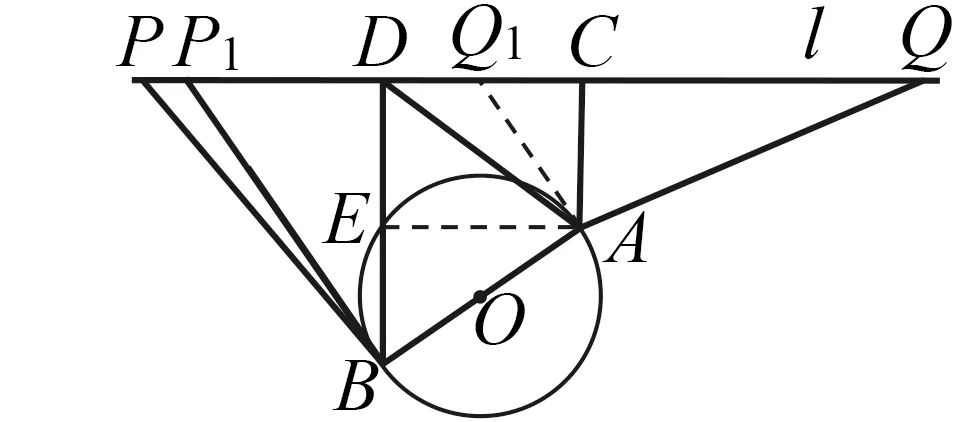
图3
(1)若P1B⊥AB,求P1B;
(2)P和Q中能否有一个点落在D处?并说明理由;
(3)若PB=QA=d,当d取最小值时,求P,Q两点间的距离.
·建构模型
问题的解决关键在于构建适切的数学模型.本题中,对“线段PB,QA上的所有点到点O的距离均不小于圆O的半径”这一关键语句的刻画显得尤为重要.
一种直白的刻画:对点P而言,若线段PB上任意一点P′,都有P′O≥r,则点P满足规划要求.这是用关于距离的不等式模型刻画点P.在这样的数学模型下,很难确定满足条件的点P所在的区域,后续的工作也就更困难.
另一种刻画:通过作图观察分析,发现当∠OBP<90°时,点P不满足规划要求,只有当∠OBP≥90°时,点P满足规划要求.这是用关于角度的不等式模型刻画点P.在这种数学模型下,不难确定直线l上满足条件的动点P只能在点P1的左侧(含点P1),满足条件的点Q只能在点Q1的右侧(含点Q1)(其中Q1A⊥AB).因此,问题(2)转化为:分别判断∠OBD和∠OAD与90°的大小关系.问题(3)转化为:点P在P1的左侧运动,点Q在点Q1的右侧运动,且PB=QA=d,当d最小时,求P,Q两点间的距离.
从高考阅卷情况来看,此题得分不高的很大部分原因是数学模型选择得不合适.由此可见,构建合理、适切、优化的数学模型是至关重要的.当然,要做到选择适切,必然要对数学模型进行分析、比较、评估和调整,这恰恰意味着选择能力的重要性.
·求解模型
此题入口较宽,关于问题(1),可以选择用平面几何法、三角函数法或者解析几何法.关于问题(2),实质就是分别判断∠ABP和∠BAD与90°的大小关系,可以用余弦定理,也可以用向量数量积来处理.关于问题(3),要说明d的最小值,不能仅仅是静态几何图形下的计算,而应着眼于其中的“变化”,即构建关于PB的目标函数模型,确定自变量的取值范围,然后求该函数的最小值.选择刻画动点P的参数,既可以是线段长度也可以是角度.限于篇幅,以下仅给出部分略解.
问题(2)中点Q能否落在点D处?
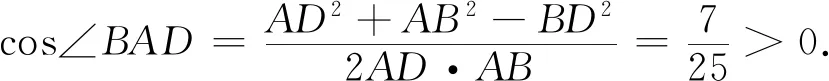
两种方法都能得到∠BAD为锐角,故点Q不能落在点D处.
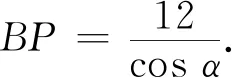
3 思考
本题就知识目标而言,考查了三角函数的应用、解方程、余弦定理、向量数量积、直线与圆等基础知识;就能力目标而言,考查了独立探究、数学阅读和表达、分析和解决实际问题等关键能力;就素养目标而言,考查了数学抽象、直观想象、逻辑推理、数学建模、数学运算等核心素养;因需要“创造”新的数学对象,故又考查了学生的创新意识、应用意识和实践能力.另外,前几年江苏卷的应用题都统一设定参数,这种函数模型的构建实质上就是“静态”地建立数学关系式,一定程度上降低了数学建模的“含金量”,而本题的参数不止一种选择,给了学生更多的选择空间.
高考数学江苏卷试题从能力立意到素养导向的转变有以下突出表现:其一,考查情境从学科知识化到真实情境化;其二,考查目标从常规性问题到探究性要求,如本题中第(2)问是方案的可行性判断,或者说是探究性说明,而不是求解论证;其三,试题要素从单一到多元,如本题是两个动点,因素就复杂了,也给学生心理造成一定的陌生感和畏惧感.
4 教学建议
2021年将有江苏、辽宁等8个省份进行新高考,数学高考都将使用全国卷.2020年高考第一次出现的全国新高考卷,无疑具有“先行一步”的示范引领意义,研究全国新高考卷,也就有重要而积极的意义.以新高考I卷为例,该卷应用性试题选择当前重大公共卫生问题、环境保护、劳动、体育、古代科学等现实生活情境、科学情境,具体见表1.

表1 2020年新高考I卷应用性试题分析
一定意义下,这些题目属于传统意义下的应用题,要解决以上问题,就要将非数学情境的问题抽象为数学问题,再用数学知识去解决.解题过程充满着抽象、判断、选择、评估、优化等一系列过程,
着力考查了数学抽象、数学建模、数学推理、数据分析等核心素养,更为重要的是,考生在解决过程中,受到德、智、体、美、劳的全面教育.可以看到,应用题考查的力度加大了,这是新高考改革的重要趋势.基于以上分析,就应用题教学给出如下建议.
4.1 关注新情境题,注重背景研究
为更好地区分和选拔人才,新高考更追求实践性,会用好的情境来考查.教学中,要经常给学生一些新颖的、紧扣时代气息的问题情境;要更多关注数学与自然科学、人文社科等其他领域的融合,注重数学与社会的紧密联系;要充分利用教材上的一些背景编拟一些应用问题,像苏教版上“阅读材料”“探究拓展”“链接”等栏目,都是较好的背景资源;要注重引导学生将实际问题抽象概括为数学问题,引领学生以数学的视角观察世界,以数学的思维思考世界,以数学的语言表达世界.
4.2 加强审题教学,提高阅读能力
应用题阅读量(文字、图形、符号)的增加是高考的大势所趋,对学生的阅读能力提出了较高要求.而这一环节往往被很多学生所忽略,他们读题时一目十行,只了解大概题意就匆忙下笔,最后导致问题百出.教学中,要提升学生的审题意识,培养学生严谨品质;在审题、阅读环节加强指导与练习,提高学生的信息提取和加工能力,必要时要求学生逐字逐句阅读,边阅读边记录,如数据可以列成表格形式,一些重要关系直接标记出来.另外,要让学生特别注意加着重号的部分或括号内的信息,这样能迅速掌握有效信息,大大提高阅读效率.
4.3 突出学生主体,留足时间空间
教学中,要让学生自主观察、探究、分析、归纳、反思、整合,让学生学会思考,在解决问题中提高能力;要留足学生“自己整理订正”的时间,让学生再发现、再提出问题,把数学探究活动推向深入;帮助学生克服对应用题的心理障碍,增强解应用题的信心.高考数学会“多考想,少考算”,在思维层次上区分考生,教学更应突出思维能力的培养,发展学生的核心素养,培养学生的理性精神,进而促进人的发展[4].
4.4 加强模型教学,固化建模程序
一般有如下的数学建模程序:(1)阅读材料,分析、筛选、处理信息,并用图形或者表格的形式呈现出来,即弄懂题意并梳理出关键信息,这是第一关——文理关;(2)对实际问题进行数学抽象,并用数学语言进行表征,这是第二关——事理关;(3)构建合适的数学模型,这是关键一环,过程中需要找到关键变量,以恰当的量(如角度或者长度)去刻画这一关键变量,建立相关诸要素之间的关系(相等关系或者不等关系),这是第三关——数理关;(4)对数学模型进行计算求解,这是第四关——算数关;(5)对计算结果进行回归检验,考查评估是否满足实际情况,若与实际相去甚远,还需改进优化数学模型并再次求解.
