“轴对称图形”教学:制作、使用“多功能角平分器”*
2020-12-17李明树江苏省苏州工业园区东沙湖实验中学215021
李明树 (江苏省苏州工业园区东沙湖实验中学 215021)
好的学具在数学教学尤其是几何教学中有着重要的作用,能够帮助学生认识问题的本质,实现思维的突破.教学苏科版初中数学八年级上册第二章“轴对称图形”时,笔者引导学生创新制作、使用“多功能角平分器”,不仅加强了学生对线段、角、等腰三角形的轴对称性的理解,而且培养了学生用数学眼光和数学思维欣赏世界、探秘世界的意识和能力.
1 “多功能角平分器”的制作
1.1 材料准备
准备吸管、工字钉若干,2 mm宽彩色细纸条一根,20 cm长细线一根,刻度尺一把,胶水一瓶,剪刀一把,记号笔一支(图1).

图1
1.2 制作步骤
(1)取吸管两根,用刻度尺量出15 cm,用记号笔在两端做好标记(图2);

图2 图3
(2)用一枚工字钉把两根吸管的一组标记点钉在一起(图3);
(3)取吸管两根,用刻度尺量出10 cm,用记号笔在两端做好标记(图4);

图4 图5
(4)用一枚工字钉把两根吸管的一组标记点钉在一起(图5);
(5)用两枚工字钉把四根吸管的剩余两组标记点分别钉在一起(图6、图7);

图6 图7
(6)用胶水和2 mm的彩色纸条在四根吸管上标记相等刻度(图8);

图8 图9
(7)调整相关彩色纸条位置,得到多功能分角器(图9).
2 “多功能角平分器”的使用案例
案例1作线段的垂直平分线
操作 已知线段AB(图10),可以利用多功能角平分器作线段AB的垂直平分线.调整多功能角平分器,使连接不相等两边的工字钉分别与点A,B重合(图11),用记号笔分别在另外两个工字钉的位置作标记C,D,作直线CD,就是线段AB的垂直平分线.
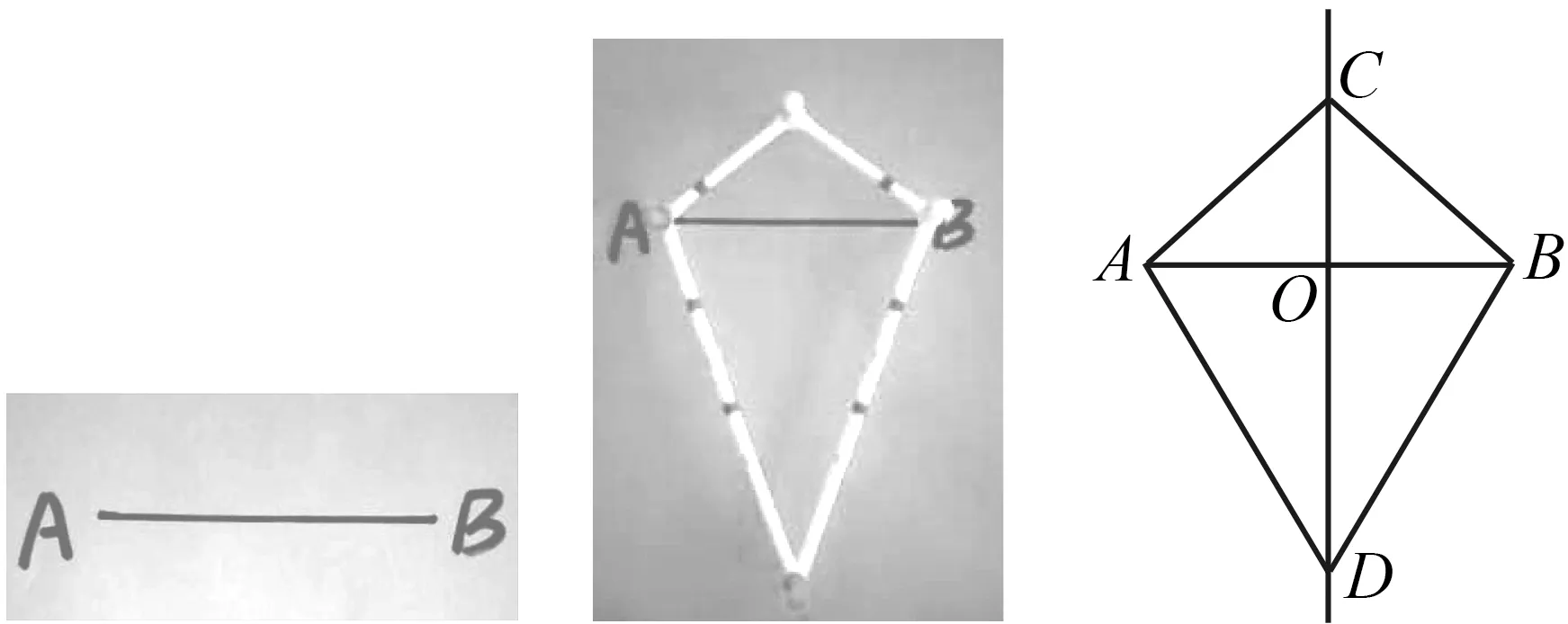
图10 图11 图12
其数学模型和简要证明如下:如图12,CA=CB,DA=DB,则直线CD是线段AB的垂直平分线.先证△ACD≌△BCD(SSS),再证△ACO≌△BCO(SAS)或者△ADO≌△BDO(SAS).
这样操作其实是基于一个命题:如果一个点到线段两端的距离相等,那么这个点在这条线段的垂直平分线上.这个命题的条件是什么,结论是什么?如何找寻到已知线段AB两端距离相等的点?找几个这样的点可以画出线段的垂直平分线?一系列的问题给学生带来了疑惑.教学中发现,部分学生用刻度尺先作出线段AB的中点D,再利用圆规作以线段AB为底边的等腰三角形的顶点C,C1,C2,C3,…(图13).然后过C,C1,C2,C3其中任意两点作直线,即得到线段AB的垂直平分线.学生作图的依据是“经过两点有且只有一条直线,即两点确定一条直线”的基本事实.那么找哪两个点最具有代表性?笔者引导学生对苏科版数学八年级上册第53页“操作”进行了再探究.教材安排环节如下:
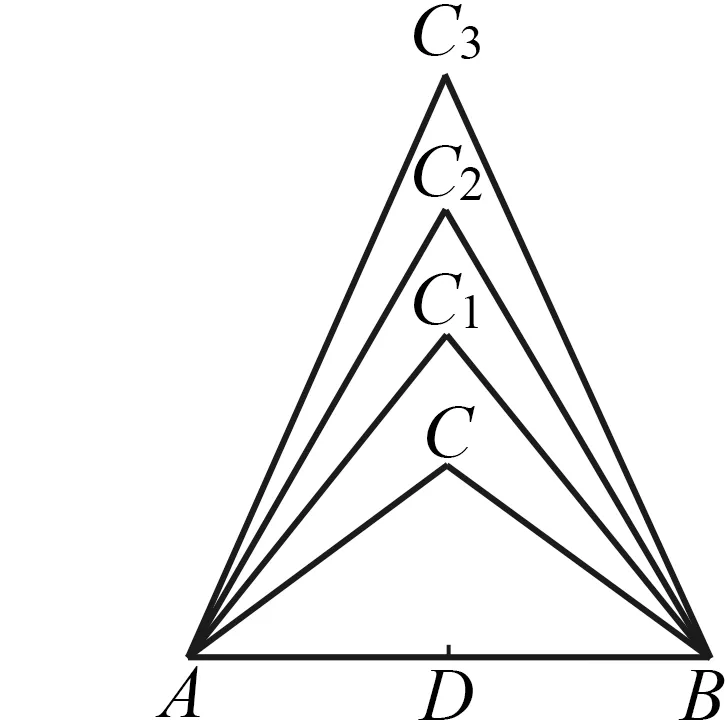
图13

作法图形1.分别以A,B为圆心,大于12AB的长为半径画弧,两弧相交于C,D.2.过C,D两点作直线.直线CD就是线段AB的垂直平分线.
教材的意图是让学生通过思考和操作找到线段两端距离相等的点,既发现到线段两端距离相等的点在线段的垂直平分线上,又能够主动利用尺规作图的方法画出图14.联系作法的步骤可发现:图14中AC=CB=BD=DA,即四边形ACBD是菱形,易证直线CD为线段AB的垂直平分线.
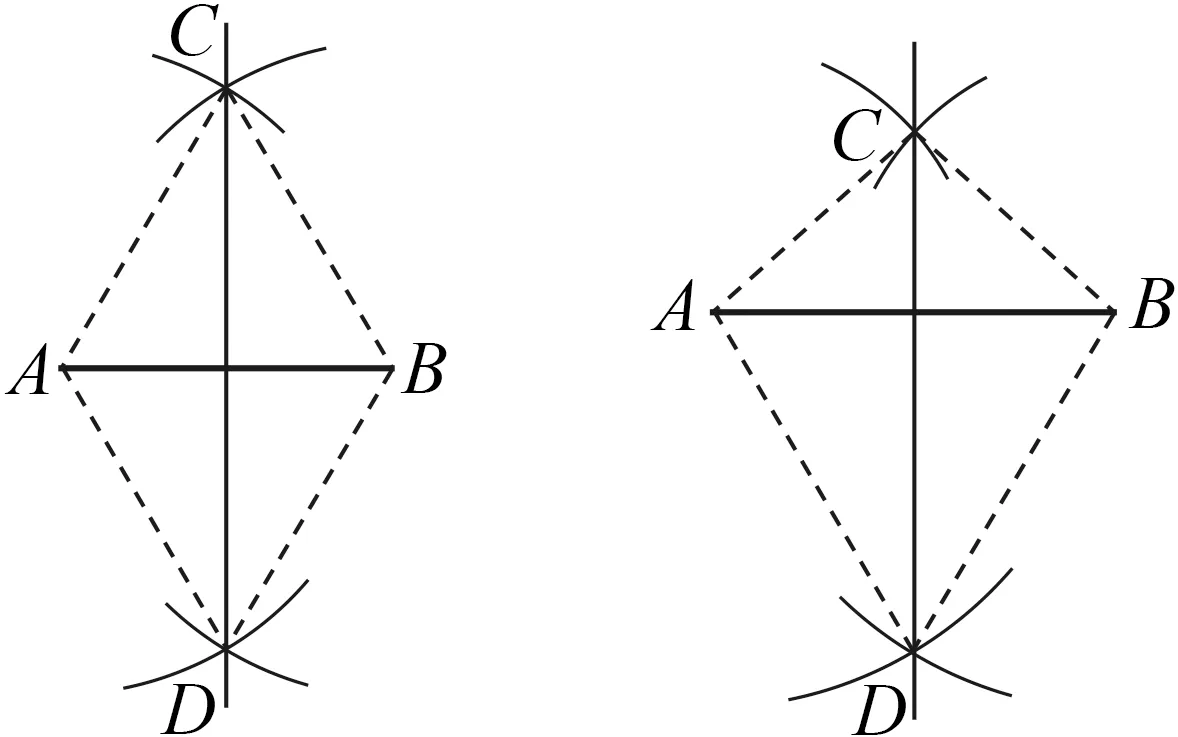
图14 图15
为了防止学生的思考偏向某种模式、帮助学生克服思维定势,教学中笔者引导学生更改作法步骤,利用案例1的操作方式:利用多功能角平分器画已知线段的垂直平分线,可以找到“线段垂直平分线上的任意两点”,帮助学生充分理解线段垂直平分线的判定定理.之后学生的作图发生了变化,不再拘泥于教材固定的作图顺序:如图15,AC=BC,AD=BD,即四边形ACBD是筝形,图中直线CD即为线段AB的垂直平分线.
案例2作已知角的角平分线.
方法1 如图16,已知∠AOB,利用多功能角平分器作∠AOB的平分线.使多功能角平分器上连接较短两边的工字钉与点O重合,较短的两边上的另外两只工字钉分别落在角的两边OA,OB上,第四个工字钉在角的内部落点记为点P(图17),则OP为∠AOB的角平分线(图18).

图16 图17
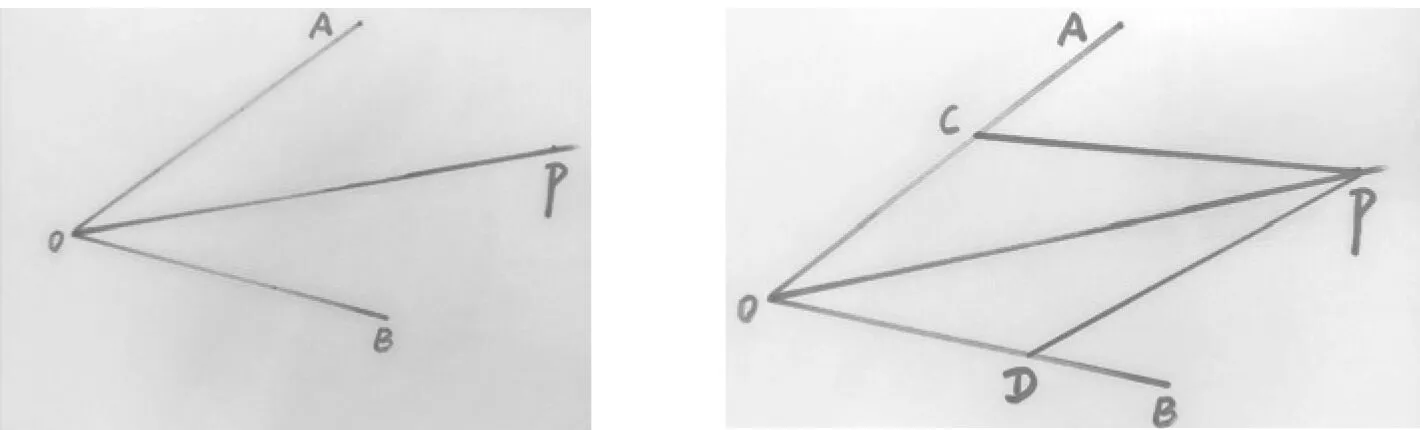
图18 图19
数学建模如图19,已知在∠AOB中,点C,D分别在边OA,OB上,且OC=OD,连结CP,DP,请说明射线OP是∠AOB的角平分线.
简证:由多功能角平分器作图步骤可知OC=OD,PC=PD,由图可得OP=OP,即可证△OCP≌△ODP(SSS),从而说明∠COP=∠DOP.
方法2 如图16,已知∠AOB,使多功能角平分器上连接较短两边的工字钉与点O重合,较短的两边分别与角的两边OA,OB重合,用记号笔分别在两边OA,OB上标记C,D两点(即OC=OD)(图20),利用多功能角平分器的较长的两边重复上述操作,并标记点E,F(即OE=OF)(图21),连结ED,CF交于点P,则OP为∠AOB的角平分线(图22).

图20 图21

图22 图23
数学建模如图23,已知∠AOB中,点E,C在边OA上,点F,D在边OB上,线段ED,FC交于点P,请说明射线OP是∠AOB的角平分线.
简证:先证△ODE≌△OCF(SAS),然后证△EPC≌△FPD(ASA),最后证△OPC≌△OPD(SSS)或者△OPE≌△OPF(SSS).
在教授苏科版数学八年级上册第55页的角平分线的判定定理时,笔者引领学生利用多功能角平分器使用上述两个方法作角平分线,既强化了全等三角形条件的应用,又探究了角的轴对称性,学生掌握了多种方法作已知角的角平分线.若继续探究下去,还可以有很多新的发现:连结EF或CD可以得出OP垂直平分线段EF或CD;甚至可以得出△EPF∽△CPD,点E,F,D,C共圆等结论.传统的数学教育重视基础知识、基本技能,这是学生打好基础的非常重要的两个方面,但只有知识技能是不够的,学生还要学会思考,还要去经历、去体验.学生在使用多功能角平分器的过程中感悟了基本思想、积累了基本活动经验,在知识技能这个基础上得到发展,这个发展其实就是让学生学会进行数学的思考.
案例3探索等腰三角形的轴对称性
操作 调整多功能角平分器,使较短的两根吸管上的三枚工字钉在同一直线上(图24),在连接较长两根吸管的工字钉上固定一根细线,用记号笔在纸上描出四个工字钉的位置,拉直细线,画出等腰△ABC及点D,则直线AD为等腰△ABC底边上的中线.这个等腰三角形是轴对称图形吗?它的对称轴是什么?线段AD是底边上的高、顶角平分线吗?

图24 图25
数学建模如图25,已知在△ABC中,AB=AC,BD=CD,请说明∠B=∠C,AD⊥BC,∠BAD=∠CAD.
简答:证明△ABD≌△ACD(SSS)即可得到∠B=∠C,∠BAD=∠CAD,易得∠BDA=∠CDA,而∠BDA+∠CDA=180°,所以∠BDA=∠CDA=90°,即AD⊥BC,而线段AD所在的直线即为等腰三角形的对称轴.
3 “多功能角平分器”的其他应用案例
既然“多功能角平分器”可以画三角形三条边的垂直平分线,三条垂直平分线的交点即为三角形的“外心”.当然还可以轻松画出任意三角形三边的中点,从而画出三角形的三条中线,三角形的“重心”就自然凸显出来了.利用“多功能角平分器”画已知角的角平分线的功能可以画出任意三角形三个内(外)角的角平分线,内(外)角平分线的交点即为三角形的“内(旁)心”.那么如何画出任意三角形的三条高线呢?笔者带领学生做了尝试:如图26,在△ABC中,利用案例1的方法画出线段AB的垂直平分线MN,延长线段AB,利用平移的方法过点C作AB的垂线,垂足为点D,则线段CD为AB边上的高.同样地,可以画出AC,BC边的高,三角形三条高所在的直线交于一点,而此交点即为三角形的“垂心”.
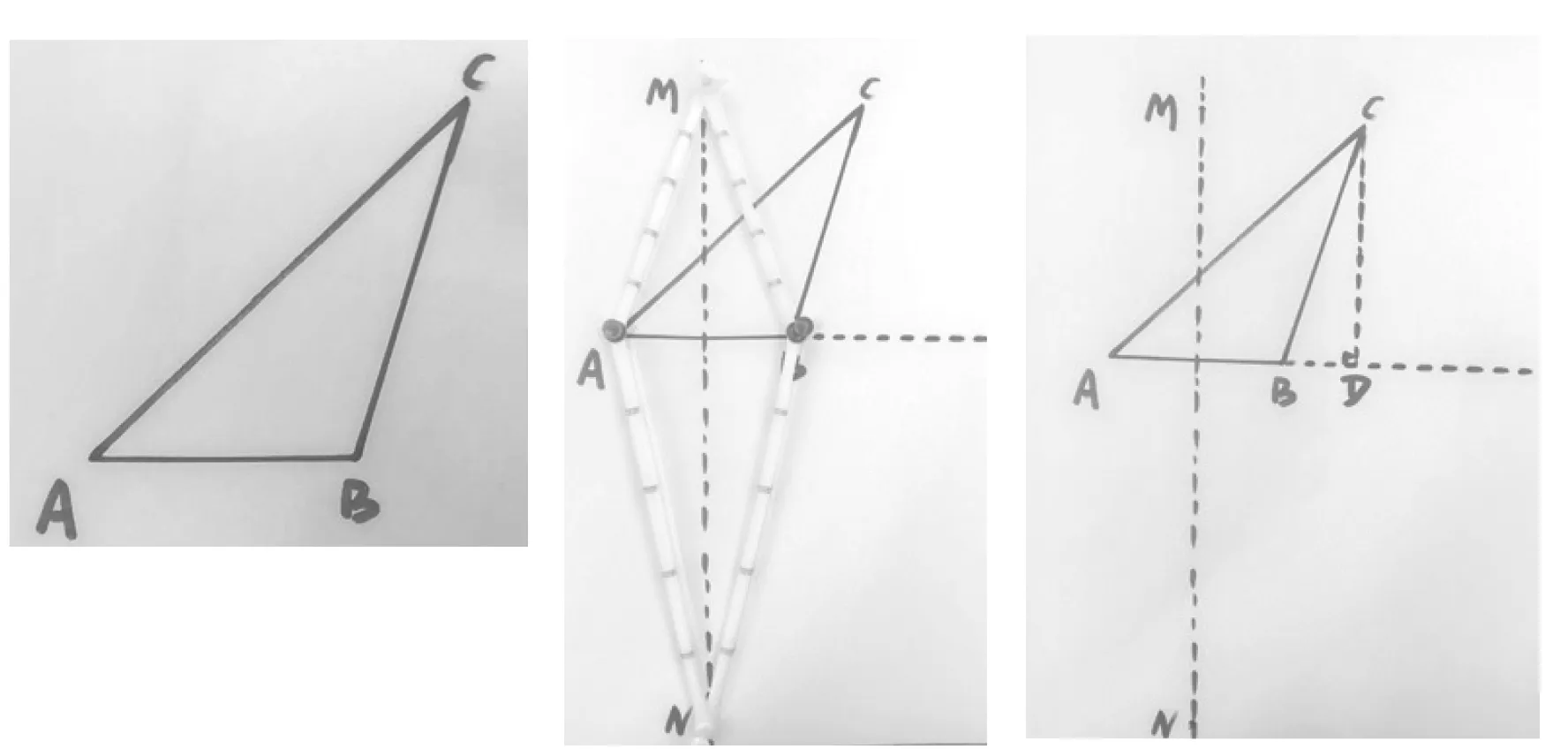
图26 图27 图28
4 学具的教学价值
“动手实践、自主探究”作为数学学习的重要方式,要求教师组织学生亲历“操作实验、观察现象、提出猜想、推理论证”等活动,从而让他们获得知识、积累活动经验、感悟数学思想.如何有效地开展操作活动,使学生养成良好的数学操作习惯,在动手实践中又能动脑思考?多功能角平分器不失为一个突破口.多功能角平分器作为教学活动的重要载体,发挥着从形象走向直观的桥梁作用.首先,学具结构的巧变促使学生在操作中进行思考.动手操作的目的在于让学生借助直观的活动来实现和反映其思维活动,若没有思维的参与,动手操作就失去了价值.借助多功能角平分器画线段的垂直平分线、画角平分线、探索等腰三角形的轴对称性及其他应用均可促进学生主动思考.其次,学具功能的隐蔽促进学生在操作中想象.动手实践不能停留于实际操作的表象,目标需指向实现活动的内化,活动内化的方式之一就是想象.如果能在直观操作的同时展开数学想象,往往能更好地培养学生的空间想象能力,发展空间观念.
教师在教学中要重视学生解决问题的创造性,通过学具的制作与使用给学生提供更多的实践机会、更大的思维空间,引导学生把操作与思维联系起来.
编者按:为密切编辑部与中学的联系,本刊编委第22次“走进课堂”,于2020年10月21日赴江苏省扬中市第二高级中学听课交流.扬中市第二高级中学是一所年轻的江苏省四星级普通高中.学校秉承“一切为了师生的发展”的办学理念,恪守“守正创新”的校训,强化党建统领,加快课程改革,完善3Z3F课程体系,致力于打造生态课堂、诗意课堂和高效课堂;实施“三化德育”,注重走特色化、多样化办学之路,积极探索“适合的教育”.近年来,学校着力提升办学层次和水平,走出了一条“低进优出”的育人之路.学校先后被评为“江苏省教育系统先进集体”“全国青少年校园足球特色学校”“江苏省校园诗教先进单位”“江苏省青少年特色科学工作室”“江苏省智慧校园”“镇江市教育现代化先进学校”“扬中市人民满意学校”“扬中市高质量发展先进集体”等150多项荣誉称号.
