谈图形运动产生的图象问题
2020-12-17黄思佳江苏省苏州工业园区星海实验中学215021
黄思佳 (江苏省苏州工业园区星海实验中学 215021)
图形在运动过程中会有很多变量,取两个相关联的变量就会产生函数,进而可以生成函数图象.有一类图形运动产生的图象问题,已成为近几年中考的热点问题.很多学生认为这类问题较难,是因为没有搞清楚图形与图象的关联,“形”与“象”分离来看,自然难以解决.如果搞清楚这类问题的解题思路技巧,其实是较容易解决的.
这节课主要让学生对问题的产生、发展和解决有一些初步的认识.
1 问题产生
如图1,四边形ABCD是边长为30 cm的正方形,等腰直角△EFG的直角边长为20 cm,边FG与BC在同一条直线上,点G与点B重合,△EFG沿BC方向向右移动,速度是2 cm/s,时间为t,点F与点C重合时运动停止,S表示三角形与正方形重叠面积,求S与t的函数关系式,并画出函数图象.
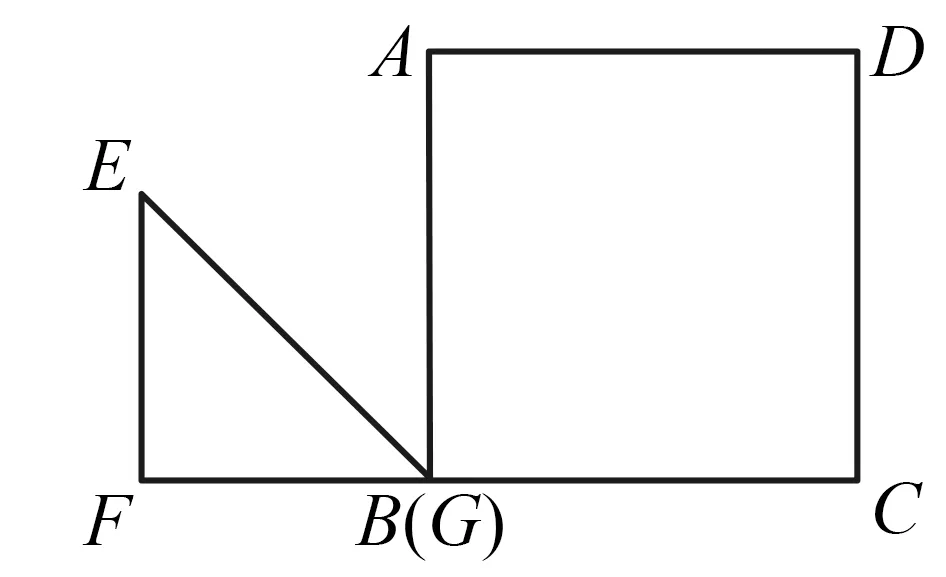
图1

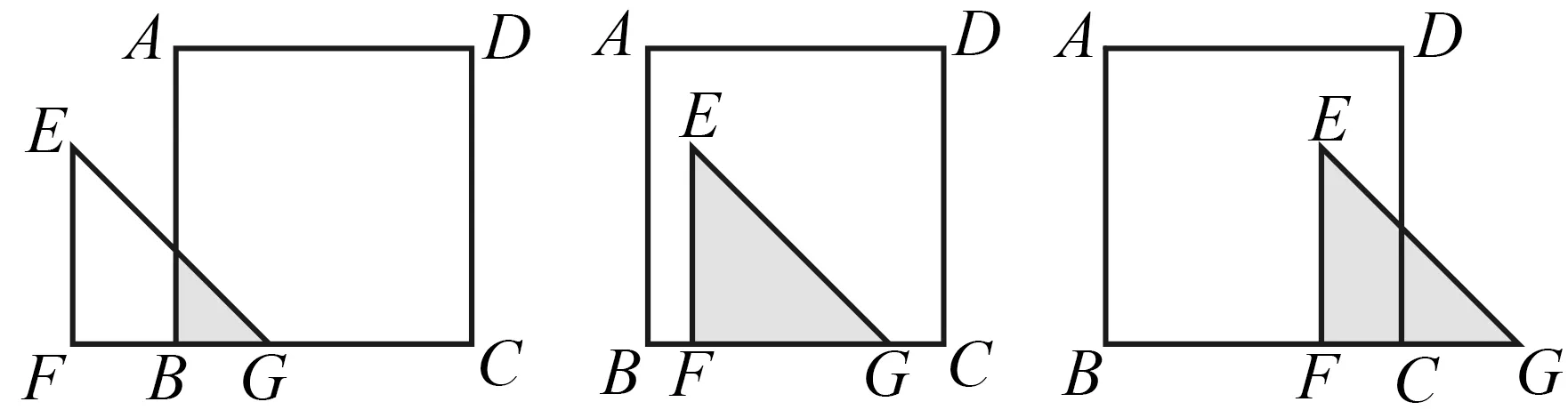
图2 图3 图4
图5
设计意图用这样一个问题引入,让学生感受图形运动,经历运动过程中两个变量之间函数关系的建立、函数图象的绘制,体会图形运动产生函数图象的关联性,理解图象的信息与图形的条件密切相关.因此,在接下来解决由图象信息探索图形运动过程的问题中,要将图形与图象对照、联系起来观察.
2 问题发展与探究
2.1 动点产生一次函数图象
问题1如图6,在矩形ABCD中,动点P从A出发,以相同的速度沿A-B-C-D-A方向运动到点A处停止.设点P运动的路程为x,△PAB面积为y,y与x的函数图象如图7所示.
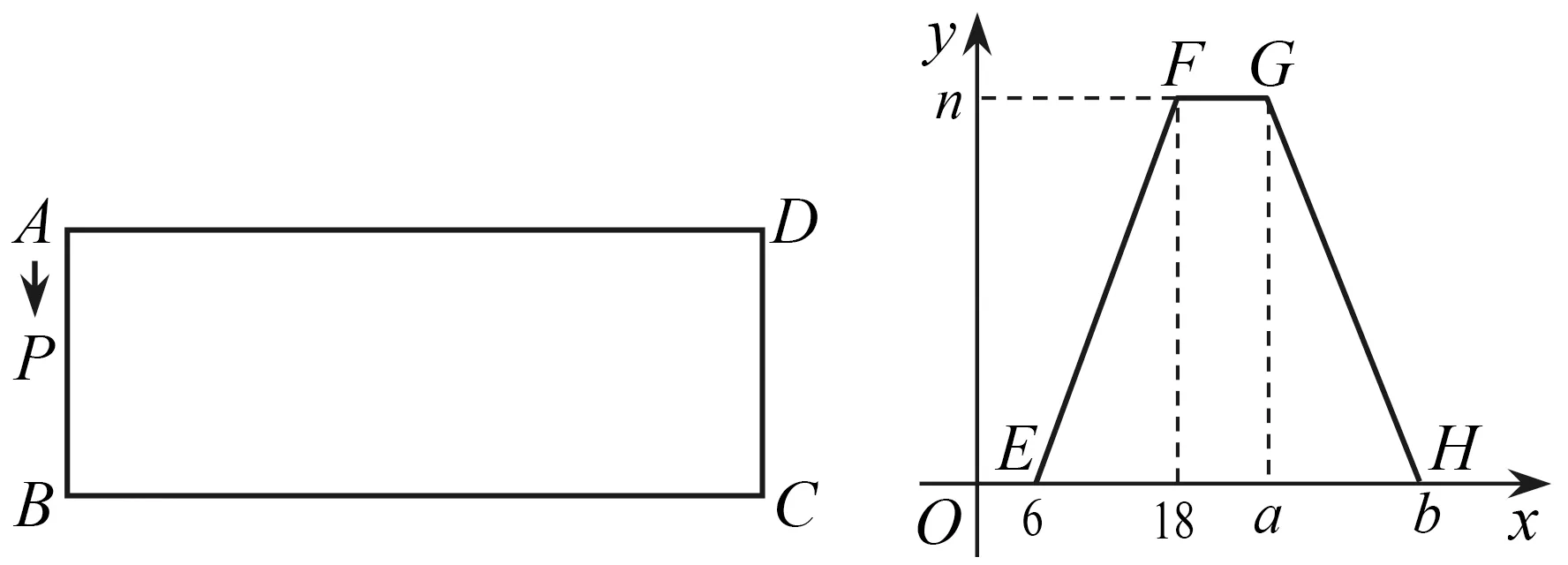
图6 图7
(1)矩形ABCD的面积为;
(2)a=,b=,n=;
(3)求x为何值时,△PAB的面积等于12?
思路分析 先整体感受图形运动,定性分析,将图形上点的运动过程与图象上的分段函数一一对应.动点在图形上运动路线发生转折时,函数图象也会随之发生转折,因此,定量研究解决问题时,需抓住图象的“拐点”,画出对应的图形,从而化动为静,将问题转化为一般的图形问题,利用拐点的信息即可求解.
图象中点E坐标(6,0),对应图形中为点P运动至点B,由此可得AB=6.图象中点F横坐标18,对应图形中点P运动至点C,因此BC=12,进而可得a,b,n的值.
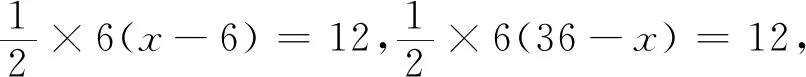
从图象来看,图象的函数解析式就是△PAB的面积与x的关系,求出EF的解析式y=3x-18和GH的解析式y=-3x+108,将y=12代入,即可求得x=10或32.
设计意图通过问题1,让学生体会解决这类问题的一般方法,明白图形和图象密不可分,认识到“拐点”的重要性和画图的必要性.
问题2如图8,A,D分别在x轴和y轴上,CD∥x轴,BC∥y轴.点P从D点出发,以1 cm/s的速度沿五边形OABCD的边匀速运动一周.记顺次连结P,O,D三点所围成图形的面积为Scm2,点P运动的时间为ts.已知S与t之间的函数关系如图9中折线段OEFGHI所示.
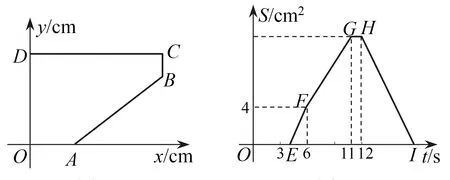
图8 图9
思路分析 与问题1进行比较,点P都是沿多边形的边运动一周,函数图象都是三角形面积与运动路程的关系,都是线性关系.两个图象极其相似,有一点区别在于动点P在五边形上运动比在矩形上运动多了一次转折,因此函数图象多了一个“拐点”.
此题作为开放题,让学生提出问题并解决.有学生提出可以利用图象上“拐点”的信息求出五边形的各边长.
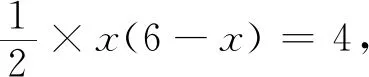
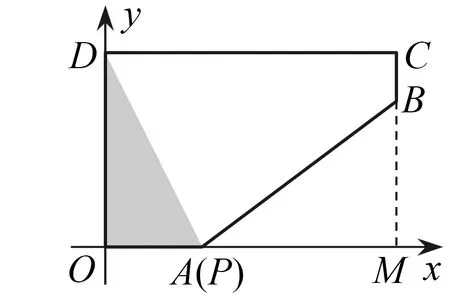
图10
还有学生提出和面积有关的问题,如求五边形的面积、求△POD面积的最大值、模仿问题1提出“t为何值时,△POD的面积为8”.此题利用图象解析式求解更为简洁.
设计意图通过问题2,让学生学会观察比较,更加深刻理解图形运动与函数图象的关系,充分利用图象中“拐点”信息求出未知.
2.2 动点产生二次函数图象
问题3如图11,菱形ABCD中,∠A=60°,点P从A点出发,以2 cm/s的速度沿边AB,BC,CD匀速运动到D终止,点Q从A与点P同时出发,沿边AD匀速运动到D终止,设点P运动的时间为t(s).△APQ的面积S(cm2)与t(s)之间函数关系的图象由图12中的曲线段OE与线段EF,FG给出.
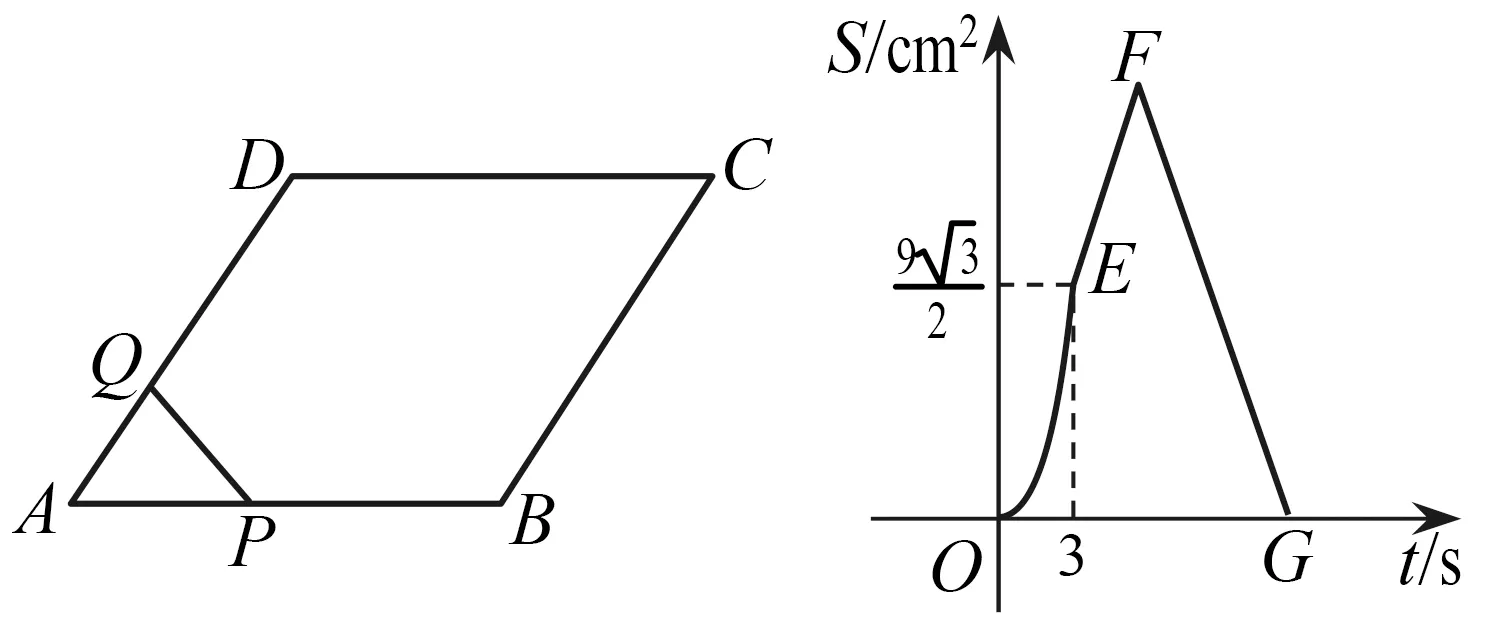
图11 图12
(1)AB=,点Q运动的速度为;
(2) 求图12中线段FG的函数关系式;
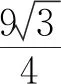
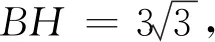
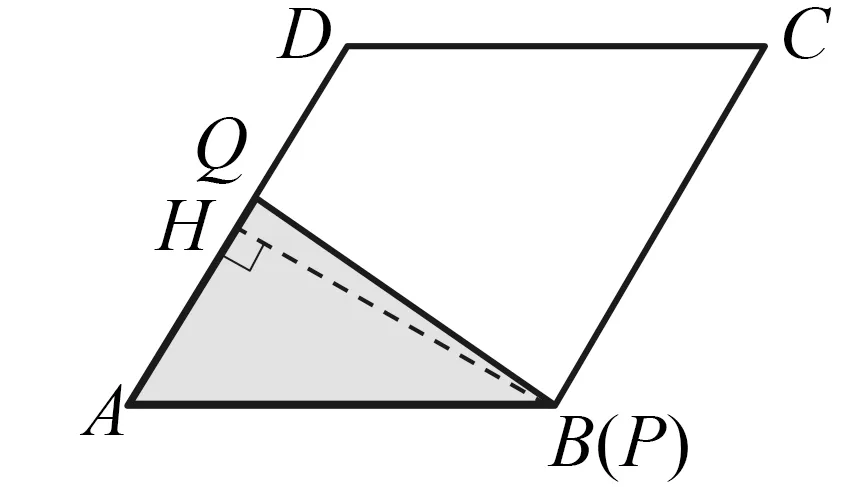
图13
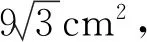
设计意图问题1和问题2的运动过程中,三角形的底是定值,高与自变量成一次函数关系,因此产生的函数图象都是一次函数;问题3中出现了底、高与自变量都是一次函数关系,则三角形面积与自变量为二次函数关系,因此图象中有一段为抛物线.让学生了解函数图象形式多种多样,它由运动中变量的关系式决定.
2.3 动点产生反比例函数图象
问题4(1)如图14,在矩形ABCD中,动点P从B点出发,沿B-C-D方向运动到点D处停止.设BP长度为xcm,点A到直线BP的距离为ycm,y与x的函数图象如图15所示.
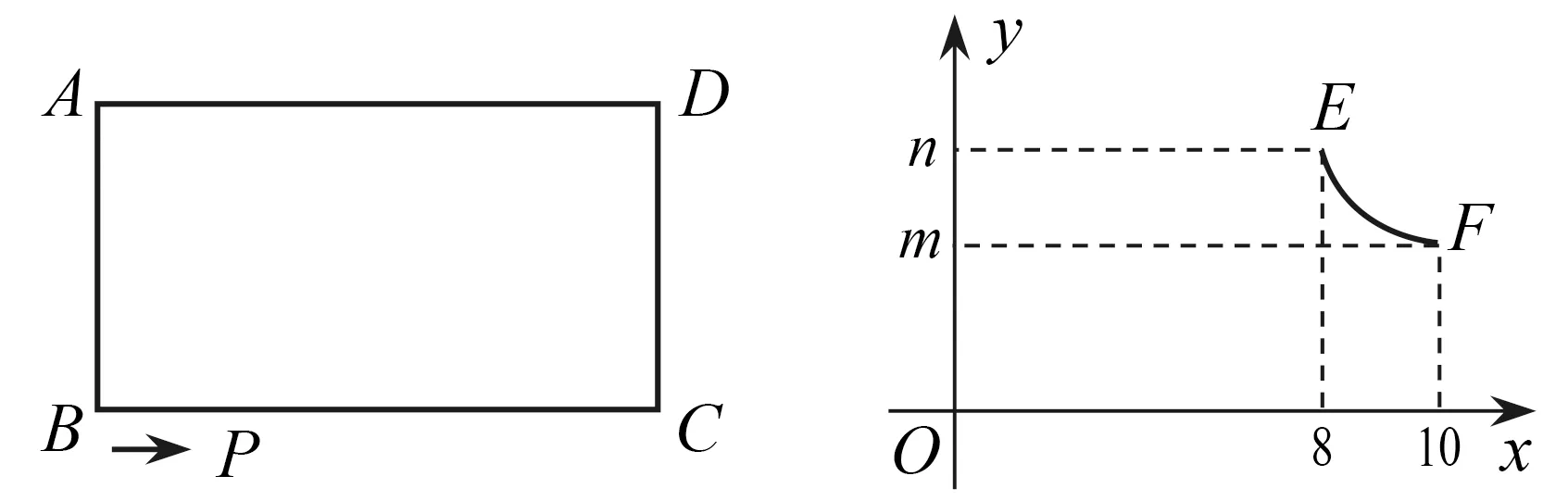
图14 图15
问:m=,n=.
思路分析 图形上点P由B运动到点C的过程中,点A到BP的距离始终为线段AB的长,所以AB=n,由图象上点E对应图形上点P运动到点C处,因此BC=8 cm.点F对应图形上点P运动到终点D处,因此BD=10 cm,从而由勾股定理得n=6,m的值为点A到BD的距离AQ,如图16.由等积法或相似可求得AQ=4.8 cm,即m=4.8,其实AB,AD,BD,AQ四条线段任意知道两条,另外两条即可求.
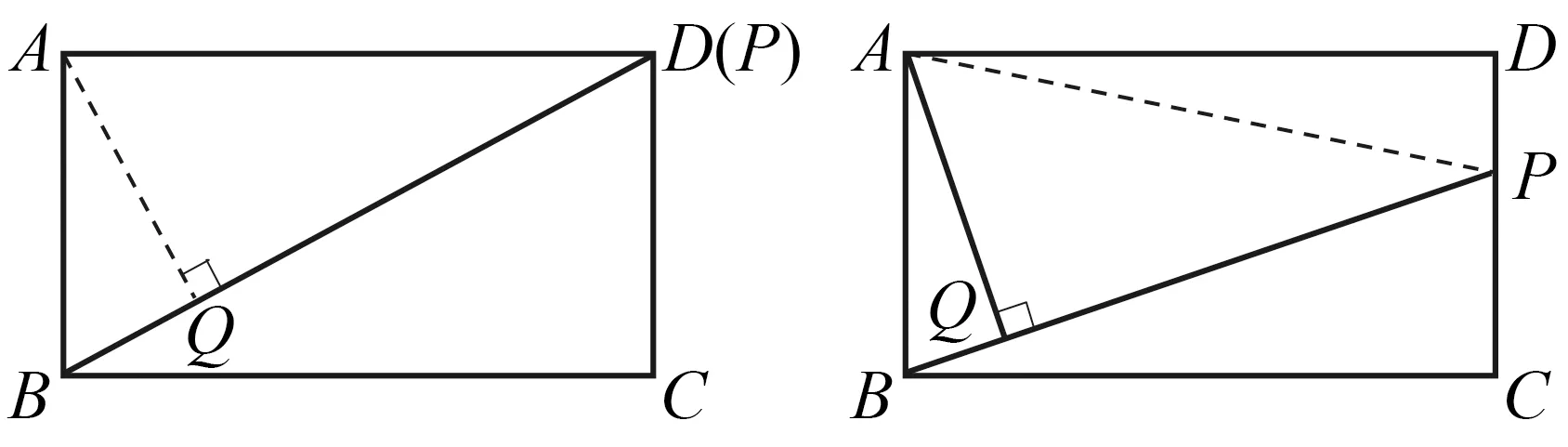
图16 图17
另外,此题需引导学生说明图象上EF段为何是反比例曲线,这样学生对图形运动产生的图象认识才更加深刻.求EF段解析式,如图17.
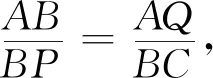
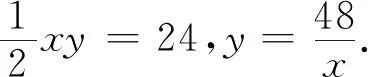
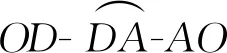
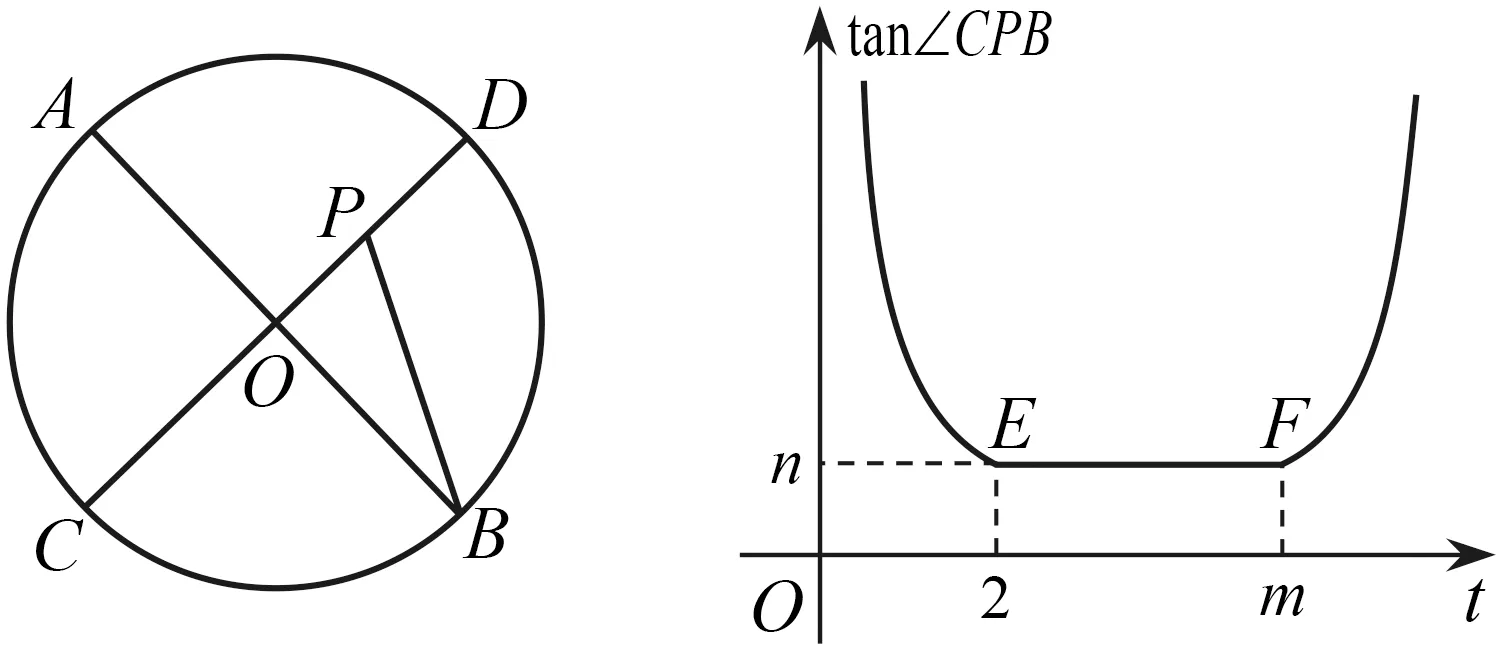
图18 图19
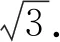
思路分析 ①图象上点E对应图形上点P运动到点D处,所以半径OD=2 cm,n=tan 45°=1,点F对应点P运动到点A处,因此m=2+π.
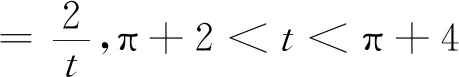
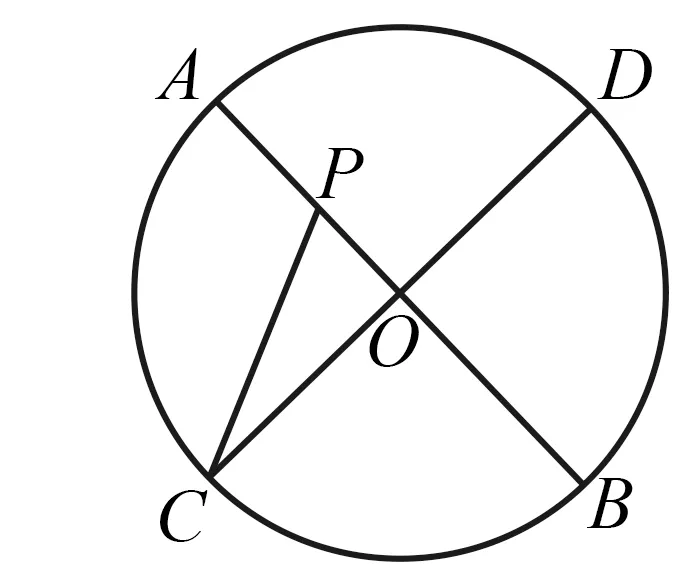
图20
设计意图如果选择的两个关联变量在运动过程中满足乘积不变,图象中就会出现反比例曲线.让学生进一步理解图象是由运动产生的,运动产生了函数,函数决定了图象;了解问题的产生和发展,掌握问题的解决策略,锻炼学生的读图能力、分析问题能力、提取信息的能力.
3 教学启示
以函数图象为背景的动态几何问题是对学生综合能力的考查.教学时,要注重问题的生成、发展和延伸,让学生经历问题的产生、体会运动的过程、培养分析的能力、掌握解题的思路方法,感受化动为静、数形结合、分类讨论等数学思想.在解决具体问题时,要培养学生画图的习惯,以这种专题探究的形式锻炼思维,提高能力,培养学生的数学素养.
