混合梁刚构桥体外预应力钢束设置与优化

林志平

（福建省高速公路集团有限公司，福州350001）

0 引 言

混合梁刚构桥是在主跨跨中处采用一段钢梁代替混凝土梁，能够有效增大传统混凝土刚构桥的跨径，并在一定程度上缓解其跨中梁体易开裂与跨中挠度过大等问题［1-2］。目前，混合梁刚构桥在国内的应用仍处于发展阶段，工程实例较少，已建成通车的仅有重庆石板坡长江大桥复线桥、温州瓯江大桥、中山小榄水道大桥、舟山鱼山大桥等，在建的福建泉州安海湾大桥预计2020年12月建成通车。

在大跨径预应力混凝土刚构桥中，为了减小混凝土拉应力，增大桥梁跨径，需要配置一定数量的预应力钢束，包括顶板钢束、底板钢束和腹板钢束等大量体内预应力钢束［3］。随着体外预应力技术的发展，体内外混合配束成为大跨径混凝土连续刚构桥的主流配束方式，它的最大优点在于体外预应力便于后期补张与更换，从而能提供更为可靠的竖向和纵向预应力，有效抑制混凝土腹板的开裂和跨中下挠［4］。马振栋等研究发现体外预应力能够有效控制大跨径连续刚构桥的跨中挠度［5］。徐栋等分析了体外预应力在大跨径连续刚构桥抗剪设计中所发挥的作用［6］。艾军等介绍了利用体外预应力对公路桥梁进行加固设计的方法［7］。皮萨尼研究了设置体外预应力的混凝土梁在长期效应作用下的力学性能［8］。邓文中等讨论了重庆石板坡长江大桥复线桥总体设计中采取的预应力钢束布置方案［9］。谢燕梅基于温州瓯江大桥对混合梁刚构桥的体外预应力线形进行了优化［10］。陈群等介绍了中山小榄水道混合梁刚构桥中体外预应力的设计思路［11］。

以往研究主要分析了体外预应力在传统大跨径混凝土刚构桥中所发挥的作用，以及现有混合梁刚构桥中体外预应力的布置方式，但对体外预应力钢束的具体作用效果与设置方法研究不多。为此，本文依托福建泉州安海湾大桥的体外预应力钢束设置，进行了相关的计算分析，得到预应力钢束的合理设置方法，为同类桥梁的设计提供参考。

1 工程概述

安海湾大桥上部结构为三跨混合梁刚构桥，总体布置如图1 所示，跨径布置为135 m+300 m+135 m，总长570 m。跨中钢箱梁吊装段长度为103 m，重1 272 t，钢箱梁两端通过5 m 长的钢混结合段与混凝土箱梁连接，目前是世界第二大跨度的混合梁刚构桥，2020 年3 月26 日全桥合龙。主梁按双幅布置，全宽33.5 m，上、下行分幅布置。主梁高度4.5～15 m，其中钢箱梁梁高范围4.535～5.869 m。墩顶梁高15 m，高跨比为1∶20，跨中梁高4.5 m，高跨比为1∶66.152。混凝土主梁、钢混结合段及钢主梁三部分梁高均按2 次抛物线规律变化。主墩采用双薄壁等截面墩，墩高22.89 m。

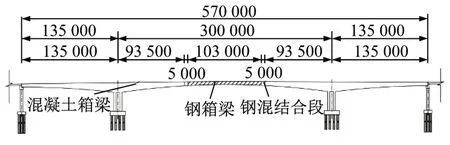
图1 安海湾大桥总体布置图（单位：mm）Fig.1 General arrangement of the Anhaiwan Bridge（Unit：mm）

安海湾大桥采用了体内外混合配束的方式。体内预应力束布置与常规混凝土连续梁相似，主要是防止混凝土箱梁出现较大拉应力。具体方法是在箱梁顶板布置纵向预应力束和横向预应力束，在腹板布置纵向下弯预应力束和竖向预应力束，在底板布置纵向合龙预应力束，体内预应力钢束随着混凝土节段悬浇逐段张拉。体外预应力主要是为防止主跨跨中下挠，其布置如图2 所示。总体上可分为混凝土梁中的体外预应力与钢箱梁中的体外预应力两部分，共设置了8 对18Φs15.2的体外预应力，沿梁中心线对称分布。体外预应力钢束沿纵桥向变化分为12 个部分，编为1～12号钢束。其中：1号为8根18Φs15.2的钢绞线；2号为 6 根 18Φs15.2 的钢绞线；3 号为 4 根 18Φs15.2 的钢绞线；4 号为 2 根 18Φs15.2 的钢绞线；5～8 号均为 2 根 18Φs15.2 的钢绞线；9 号为 2 根 18Φs15.2 的钢绞线；10 号为 4 根 18Φs15.2 的钢绞线；11 号为 6根 18Φs15.2 的钢绞线；12 号为 8 根 18Φs15.2 的钢绞线。成桥时体外预应力钢束仅张拉控制应力的30%（即558 MPa）。

图2 安海湾大桥体外预应力布置（单位：mm）Fig.2 Layout of the external prestressing tendons in the Anhaiwan Bridge（Unit：mm）

2 体外预应力钢束的作用效应分析

2.1 计算分析方法

建立全桥板壳-实体有限元模型，混凝土箱梁采用SOLID95 实体单元模拟，钢箱梁采用SHELL181 板壳单元模拟，预应力钢束采用LINK10 单元模拟，全桥模型单元数量约60 万个，结构整体模型如图3所示。

图3 安海湾大桥板壳-实体有限元模型Fig.3 Shell-solid finite element model of the Anhaiwan Bridge

2.2 设计线形体外预应力总体效应

首先计算仅在自重荷载作用下，钢箱梁段整体的竖向位移如图4 所示，中部位移大而端部位移小，跨中竖向位移最大，为641.8 mm；最小位移发生在端部，为429.2 mm。

图4 自重作用下钢箱梁部分竖向位移图（单位：mm）Fig.4 Deflection of steel girder under self-weight（Unit：mm）

在自重荷载作用下，部分混凝土箱梁截面应力如图5 所示，截面上缘受拉而下缘受压，越靠近中墩的截面应力越大。墩顶附近截面的最大压应力为17.55 MPa，最大拉应力为18.35 MPa；混凝土梁中部附近截面最大压应力为15.58 MPa，最大拉应力为10.01 MPa；结合段附近截面最大压应力为13.12 MPa，最大拉应力为3.87 MPa。

当再考虑体外预应力作用时，钢箱梁跨中竖向位移为628.72 mm，钢箱梁端部位移为421.2 mm。对比计算结果，施加体外预应力能够有效减小钢箱梁跨中和端部挠度分别为13.1 mm、8.0 mm。此外，设置体外预应力使得下缘压应力减小幅度为0.20～0.30 MPa、上缘拉应力减小幅度为0.80～1.00 MPa。

2.3 体外预应力效应局部分析

由于体外预应力钢束主要由混凝土箱梁段的钢束和钢箱梁段的钢束构成，因此将二者分别施加至主梁上，进一步分析二者对于减小跨中挠度所能做出的贡献。

图5 自重作用下部分混凝土箱梁截面应力图（单位：MPa）Fig.5 Stress diagrams of concrete girder sections under self-weight（Unit：MPa）

2.3.1 混凝土箱梁段体外预应力

在体外预应力初始线形的基础上，去掉钢箱梁段的体外预应力，仅保留混凝土箱梁段的体外预应力，包括 1～7 号及 9 号、10 号钢束，具体线形如图6所示。

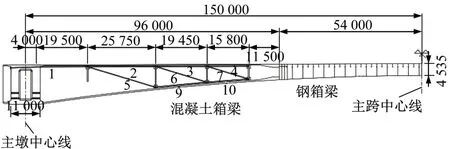
图6 混凝土箱梁段体外预应力线形（单位：mm）Fig.6 Layout of the external prestressing tendons in concrete girders（Unit：mm）

在自重与体外预应力共同作用下，钢箱梁段跨中位移减小9.7 mm，端部位移减小9.4 mm，占据了体外预应力总效应的74.50%与117.94%。

此外，相较于设计线形的体外预应力作用，仅布置混凝土梁段范围体外预应力，混凝土梁截面下缘压应力减小幅度降低，而上缘拉应力减小幅度提高，有利于梁段受力。

2.3.2 钢箱梁段体外预应力

在体外预应力初始线形的基础上，去掉混凝土箱梁段的体外预应力，仅保留钢箱梁段的体外预应力，为了保证预应力的有效性，将线形延伸至混凝土箱梁中最接近钢梁的转向块内，包括8 号、11号及12号钢束，具体线形如图7所示。

图7 钢箱梁段部分体外预应力线形（单位：mm）Fig.7 Layout of the external prestressing tendons in steel girder（Unit：mm）

计算表明，仅施加钢箱梁段体外预应力时钢箱梁段跨中位移减小3.3 mm，端部位移增大了1.5 mm；同时，混凝土梁截面下缘压应力降低，而上缘拉应力提高；而对于结合段附近截面，拉压应力均一定程度增大；不利于梁段受力。

初始线形下体外预应力总用量为2.95 m3，混凝土箱梁体外预应力总体积为1.65 m3，占比56%；钢箱梁体外预应力总体积为1.30 m3，占比44%。对于减小钢箱梁跨中竖向位移，混凝土箱梁体外预应力贡献了75%，而钢箱梁部分贡献了25%。并且，混凝土箱梁的体外预应力能一定程度上改善混凝土梁的受力。因此，将材料用量与实际贡献对比可知，在混凝土箱梁设置体外预应力更加经济有效。

结合混合梁刚构桥的弯矩分布可知，当钢箱梁长度与主跨长度比例为0.36 时，恒载作用下中跨混凝土梁以受负弯矩为主，钢箱梁则以受正弯矩为主。同时由于采用了钢箱梁，跨中正弯矩较小，因此，在混凝土段设置预应力能更有效地减小钢箱梁段的竖向位移。

根据上文分析，施加体外预应力在一定程度上可以减小钢箱梁竖向位移，尤其是跨中截面的竖向位移。若要进一步发挥体外预应力的经济性和有效性，应该将体外预应力的布置优先集中在混凝土箱梁中；而结合段附近体外预应力有助于增大压应力，使钢-混结合更紧密，因此保留8 号与11 号钢束，并锚固至结合面处。得到初步优化线形如图8所示。

图8 体外预应力初步优化线形（单位：mm）Fig.8 Initial optimization of layout of the external prestressing tendons（Unit：mm）

2.4 体外预应力效应逐段分析

为进一步分析每根体外预应力所发挥的作用，取如图9 所示的3 段钢束，分别建模，分析1号、5 号与9 号钢束单独作用时的效应，位移结果表1所示。

图9 体外预应力优化分析线形（单位：mm）Fig.9 Layout of the external prestressing tendons for analysis（Unit：mm）

表1 体外预应力位移效应逐段分析Table 1 The displacement effects of every external prestressing tendon mm

由表中数值看出：1 号钢束作用下，钢箱梁跨中位移减小8.3 mm，端部位移减小6.7 mm；墩顶附近截面下缘压应力有所减小，而上缘拉应力明显减小。5 号钢束作用下，钢箱梁段跨中位移增大了0.3 mm，端部位移增大了0.03 mm；混凝土梁段的中间截面附近最大压应力有所增大。9 号钢束作用下，钢箱梁段跨中位移增大了2.4 mm，端部位移增大了1.4 mm；混凝土梁段受力基本不变。由此可见，布置在靠近箱梁顶板附近的1 号钢束对改善跨中梁体下挠的效果最好；而沿底板附近布置体外预应力反而增加了梁体跨中的下挠，主要原因是该段预应力钢束在向跨中呈斜向上的线形造成的。

3 体外预应力钢束优化

3.1 优化方案

通过对体外预应力钢束的局部分析，可以发现将体外预应力布置在混凝土箱梁段内更有效，从而得到了如图8 所示的初始优化线形。进一步以1 号、5 号与9 号钢束为例进行受力分析，将混凝土箱梁段内的体外预应力钢束分为顶板平行束、斜向束及底板平行束三部分，可知1～4号顶板平行束能减小钢梁位移且优化混凝土段受力，5～8 号斜向束对混凝土段受力有利，9～11 号底板平行束则不利于钢梁位移减小。因此，在初始优化线形的基础上，去除混凝土箱梁中的底板平行束，即保留1～8 号钢束，得到最终优化线形如图10所示。

图10 体外预应力优化线形（单位：mm）Fig.10 Optimal layout of the external prestressing tendons（Unit：mm）

3.2 优化线形下体外预应力效应

在自重与优化后的体外预应力作用下，钢箱梁竖向位移中间大而两边小，最大竖向位移发生在跨中，为625.7 mm；最小竖向位移发生在端部，为416.6 mm。从而与自重作用下相比，钢箱梁段跨中位移减小16.1 mm，端部位移减小12.6 mm。相较于原始体外预应力线形作用下的结果，二者分别扩大了23.3%与58.1%，有效性显著增强。

在改善一般混凝土梁截面受力方面，与设计线形相比，截面下缘压应力减小幅度更小，为0.10～0.25 MPa；而截面上缘拉应力减小幅度则有所增大，为1.15～1.50 MPa；并且结合段附近截面拉压应力均减小。总体而言，优化线形的体外预应力布置方式更有利于结构受力。

4 预应力钢束索力调整预案

传统大跨径预应力混凝土连续刚构桥在使用过程中，由于收缩徐变等长期效应影响，跨中挠度会大幅度增加，影响其正常使用功能。为了探究混合梁刚构桥在长期效应下的变形，利用有限元模型进行模拟。由于成桥时体外预应力张拉应力仅为控制应力的30%（558 MPa），因此当使用过程中出现较大挠度，可以对体外预应力进行再张拉，以减少主跨的挠度。在考虑混凝土10年收缩徐变的基础上，分别将体外预应力再张拉至控制应力的40%（744 MPa）、50%（930 MPa）、60%（1 116 MPa）、70%（1 302 MPa）及75%（1 395 MPa），计算各自的作用效果，计算结果如表2 所示，与长期作用导致的位移增大值相比，跨中位移减小程度较小，且呈线性增长，可根据实际的挠度变化选择合适的调整预案。

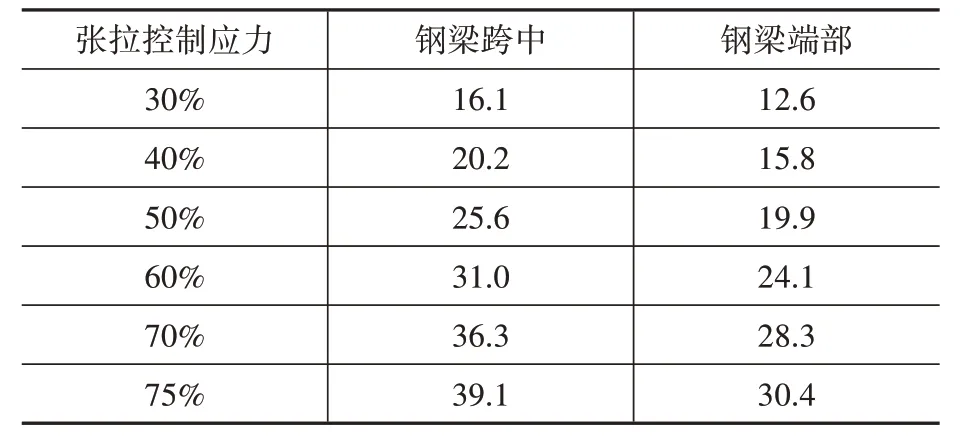
表2 不同张拉控制应力下钢梁段竖向位移减小值Table 2 The deflection decreases under different tension control stresses mm

5 结 论

（1）本文以泉州安海湾大桥为背景工程，通过有限元方法，对体外预应力在减小混合梁刚构桥跨中钢梁段竖向位移，以及改善混凝土段受力性能中所能发挥的作用，进行了整体与局部的分析。

（2）通过有限元模型逐段分析体外预应力的效应，以改善跨中钢梁挠度和混凝土梁体受力为原则，对体外预应力的布置进行优化，发现仅保留混凝土梁段中的顶板水平束及斜向束时，体外预应力所能发挥的效果更好。

（3）计算了安海湾大桥在收缩徐变等长期效应作用下再张拉体外预应力时跨中钢箱梁的变形，得到不同体外预应力再张拉调整预案对减小钢梁竖向位移的作用。