基于连接单元的无屈曲波纹钢板剪力墙弹性简化分析模型研究

姜文伟 任记波 ，* 钱 鹏 童 骏 高晓耕

（1.华东建筑设计研究总院，上海200002；2.上海超高层建筑设计工程技术研究中心，上海200002；3.同济大学土木工程学院，上海200092）

0 引言

在现有多高层钢结构建筑抗震设计中，框架-支撑、框架-剪力墙等形式的双重抗侧力体系应用十分广泛，其中支撑、剪力墙作为主要抗侧力构件在地震作用下除了为结构提供侧向刚度外，还兼具耗能作用。相对于支撑而言，钢板剪力墙具有较大的初始刚度和良好的塑性性能［1］，但其易出现面外屈曲导致截面无法进入全截面塑性从而实现充分耗能。为解决该问题，李国强等提出了一种新型钢板剪力墙［2］，即无屈曲波纹钢板剪力墙（NCW，以下简称波纹墙），其由边缘构件和波纹钢板组成，墙体通过钢板波纹的形式提高墙体面外刚度，防止屈曲先于屈服发生，耗能能力相较于平板钢板墙更好［3-4］。

但是在设计人员进行结构设计时，波纹墙的复杂几何形式使得有限元的建模耗时耗力，因此有必要提出一种简化的模型取代精准的有限元模型。这种简化模型要求能够反映真实的边缘构件内力，与波纹钢板墙有着相同的抗侧移刚度，能够用构件屈服来模拟波纹墙的屈服，且形式需要尽可能简单。

本文根据波纹墙的受力特性，提出了多种简化模型，在比较了不同的基于连接单元的简化分析模型模拟效果后，最终选取了水平轴向连接单元模型，通过理论计算算出了模型中连接单元高度的推荐取值，并利用有限元模拟验证了其准确性。针对钢板厚度、区格高宽比、边柱及横梁的刚度对简化模型模拟效果的影响进行了参数化分析，考察该模型的普适性。最后，通过在多层多跨的算例下，分别应用波纹墙和简化模型，评估了在竖向荷载与水平荷载作用下简化模型对结构变形和构件内力的模拟效果，并给出了边缘构件内力的修正方法。

1 波纹钢板的抗侧刚度

波纹钢板墙的波纹形状参数如图1 所示，墙体波纹板采用水平放置的形式。根据波纹形状可以看出，由于“手风琴效应”，波纹钢板在顺波纹方向其刚度基本为零，无法承担轴向荷载，而在垂直于波纹方向具有较大的刚度。因此波纹钢板不能承担竖向荷载，仅承受水平荷载。

波纹钢板轴向刚度Kv=0，水平抗侧刚度分析如下。

图1 波纹形状参数示意图Fig.1 Corrugated shape parameter diagram

依据板的剪切变形特点，单波的剪切刚度［7］计算公式如式（1）所示：

式中：t为波纹钢板厚度；E为钢材弹性模量；B为波纹墙跨度；ν为钢材泊松比。

墙体由多个波纹串联形成，其抗侧刚度为

式中，n为串联的单波数量。

本文分析所采用波纹钢板波形参数如表1所示。

表1 波纹钢板墙波形参数Table 1 Corrugated steel wall waveform parameters

2 简化分析模型

2.1 几种简化分析模型

姜文伟等［8］对波纹钢板墙的简化分析模型进行了深入的研究，针对常用设计软件中的弹性和弹塑性分析提出了相应的简化模型。其中连接单元模型概念清晰，传力路径明确，建模方便，连接单元采用Bouc-Wen本构关系模型，塑性性能模拟结果良好。

为此本文在弹性分析中引入连接单元模型以模拟波纹钢板墙，并提出了以下几种简化分析模型。

2.2 简化分析模型优选

本节建立单个满跨波纹钢板墙模型以评估各个简化分析模型的模拟效果（图2），墙体参数如图3 所示。其中波纹板有限元模型采用通用有限元软件ABAQUS分析。

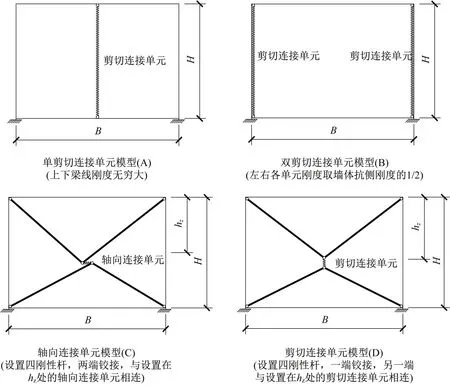
图2 几种简化分析模型Fig.2 Several simplified analysis models

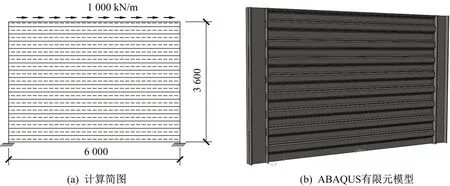
图3 波纹钢板墙分析模型（单位：mm）Fig.3 Corrugated steel wall analysis model（Unit：mm）

在顶部梁施加大小为1 000 kN/m 的均布水平荷载，四种简化模型与有限元模型的轴力分布如图4 所示。其中模型C、D 的高度参数hz暂取H/2。

柱顶变形和柱底轴力的比较结果如下。

可以看出，不论是柱顶位移还是柱底轴力，C、D 模型都要优于A、B 模型。主要原因在于模型A和模型B对波纹钢板墙的受力模式模拟不准。波纹钢板墙在承受水平荷载时，剪力主要由波纹钢板承担，倾覆弯矩则应由竖向边缘构件承担。而模型A 中将梁设置为了无限刚性，影响了整体刚度，且模型A和B中剪切连接单元承担了大部分倾覆弯矩，竖向边缘构件无法提供有效的抗侧刚度。

对C、D 模型，两模型结果差异较小，但剪切连接单元承担水平剪力的同时会产生较大的附加弯矩，影响内力在两边缘构件之间的分配，受力机理不清晰。

依据模拟构件尽量不影响原有构件的原则，以及内力对比的结果，综合选择轴向连接单元模型作为波纹钢板墙的简化分析模型。

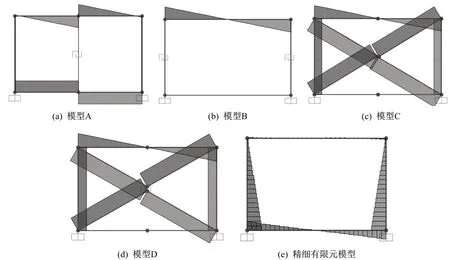
图4 各模型构件轴力图Fig.4 Axial force diagram of each model

3 轴向连接单元模型

3.1 参数h的优化

从图5 中可以看出，简化分析模型结果还存在一定误差，其与柱顶的距离h需进一步分析确定。

图5 简化模型分析结果对比Fig.5 Simplified model analysis results comparison

波纹钢板墙在承受水平荷载时，会对底部截面产生剪力和弯矩。其中剪力由波纹钢板承担，而由于波纹钢板竖向刚度为零，弯矩由左右边缘构件的轴力平衡。边缘构件的轴力分布如图6所示。

截取图6中所示虚线以上部分，有平衡方程：

式中：V是水平剪力；h是与选取截面有关的变量。

图6 波纹钢板墙模型受力简图Fig.6 Corrugated steel wall model force diagram

对轴向连接单元模型，选取图7 中虚线上部为一整体，有

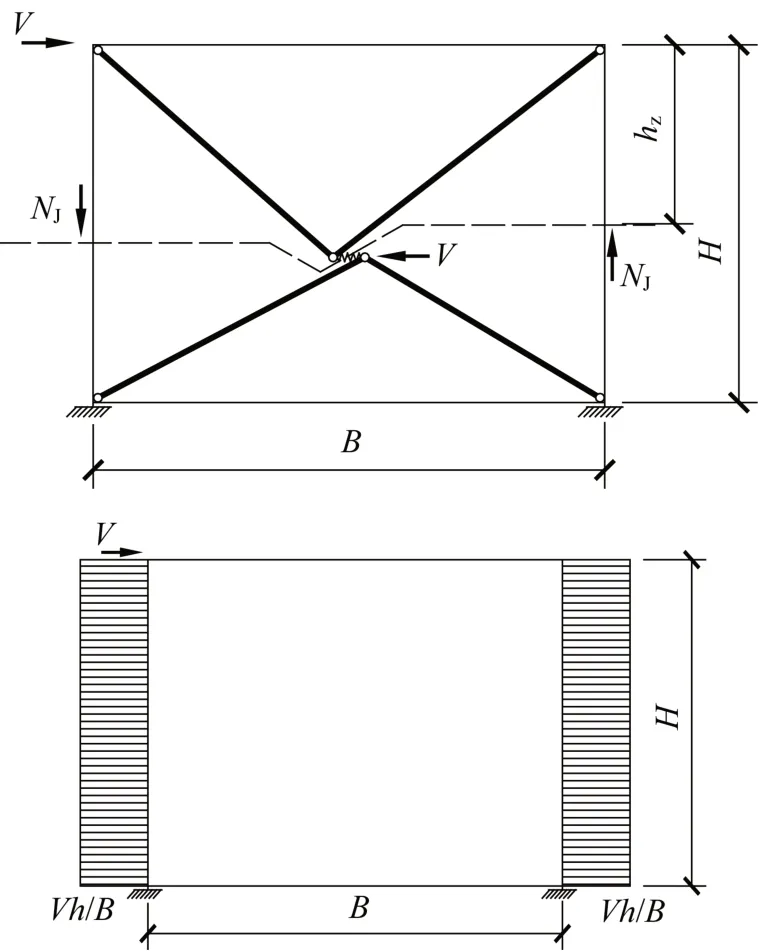
图7 简化模型受力简图Fig.7 Simplified model force diagram

式中，hz是连接单元距离顶部梁的高度。

考虑波纹钢板墙模型与简化模型的边缘构件在水平荷载V下有相同的顶点水平位移，由图乘法公式，边缘构件受力产生的顶点侧移

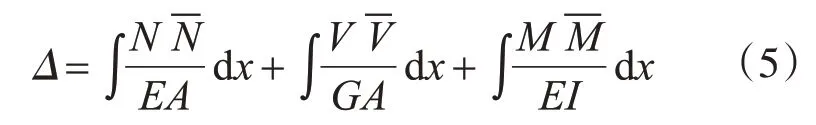
忽略剪切变形和弯曲变形：

采用图8 所示计算模型，波纹钢板厚度取为8 mm，将大小1 000 kN/m 水平荷载为均布施加在梁上。对参数变化范围内简化模型和波纹钢板有限元模型进行比较。

从结果可以看出，hz取0.60H时误差最小，证明理论分析得到的高度取值合理，轴向连接单元简化模型中应取

3.2 模型参数化分析

图8 hz/H对模拟精度的影响Fig.8 hz/H effect on simulation accuracy

考虑到不同参数对简化模型模拟效果存在一定影响，本节针对厚度、高宽比以及边缘构件刚度等参数进行了参数化分析。以下模型荷载均采用施加在顶部梁上1 000 kN/m的水平荷载。

考虑如下参数对简化分析模型的影响：墙厚t、高宽比H/B、边缘构件刚度及框架梁刚度。对比结果如图9 所示，可以看出随着参数变化，简化分析模型与精细化模型的结果接近，误差在6%以内。

4 结构算例分析

本节针对轴向连接单元简化分析模型在钢框架-无屈曲波纹钢板剪力墙结构的应用效果进行分析，评估结构在各向荷载作用下简化模型的模拟精度。

4.1 结构模型

钢框架-无屈曲波纹钢板剪力墙结构是通过在框架中布置一定数量的波纹墙以提高结构刚度及延性的结构形式，具有建筑平面布置灵活、侧向刚度大、耗能能力强等优点。对于满跨布置的波纹钢板墙，框架柱和框架梁兼做墙体边缘构件。

选取图10 所示的五层三跨的一榀平面框架，其中柱距为6 000 mm，层高4 200 mm，波纹钢板厚度取为10 mm，建立结构对应的波纹墙有限元模型和简化模型。

4.2 水平荷载下模拟精度

根据框架中震计算结果，对各层施加规定水平力如表2所示。

4.2.1 结构变形

楼层水平位移结果对比如图11所示。

图9 墙体参数对简化分析模型的影响Fig.9 Influence of wall parameters on simplified analysis model

图10 有限元模型与简化模型示意图（单位：mm）Fig.10 Schematic diagram of finite element model and simplified model（Unit：mm）

可以看出，两种模型的位移曲线吻合良好，简化模型的结果满足精度要求，各层位移结果误差在8%以内。

4.2.2 边缘构件内力

取轴②的边缘构件，其每层构件底部轴力对比见表3。

表2 各楼层规定水平力Table 2 Horizontal force on each floor

图11 楼层水平位移结果对比Fig.11 Comparison of floor horizontal displacement results

表3 边缘构件内力对比Table 3 Edge member internal force comparison

在有限元模型中，轴力不是均匀分布，而在简化模型中，轴力沿柱长均匀分布，因此需要进行修正。在有限元模型中，柱底截面弯矩由两柱轴力产生抗倾覆弯矩，在简化模型中，本层一部分倾覆弯矩通过轴向连接单元被传递至下层柱，因此需要将这部分通过式（7）修正：

式中：NPi为第i层线性修正后的柱底轴力；Ni为简化模型第i层的柱轴力；Pi为简化模型第i层轴向连接单元轴力；z为连接单元距离柱底的高度；B为波纹墙跨度。

修正后的误差在4%以内，精度满足要求。

4.2.3 非边缘构件内力

取轴①框架柱及轴①、轴②框架梁，其内力对比见表4、表5。可以看到，框架梁和框架柱的内力误差均在10%以内。

表4 水平荷载下框架梁内力对比Table 4 Comparison of internal forces of frame beams under horizontal loads

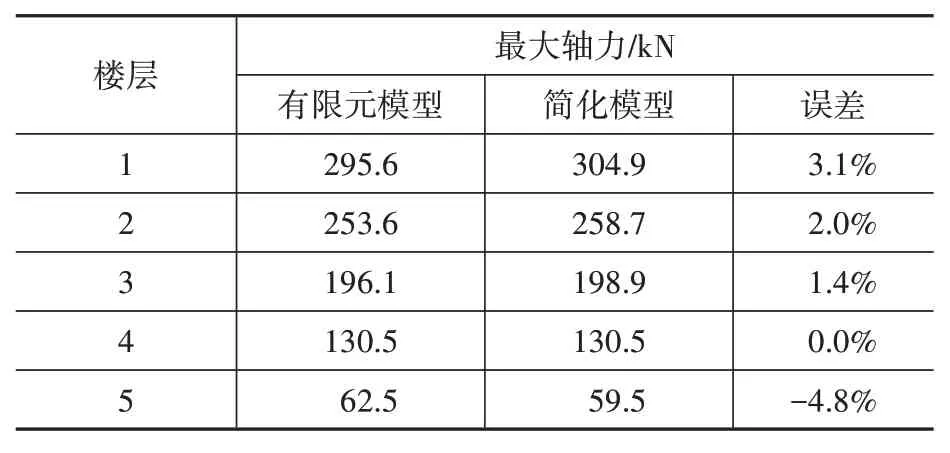
表5 水平荷载下框架柱内力对比Table 5 Comparison of internal forces of frame columns under horizontal load

4.3 竖向荷载下模拟精度

仍以图10 结构为例，对框架梁施加竖向均布荷载1 000 kN/m。

4.3.1 边缘构件内力

取轴②的边缘构件，轴力对比如表6 所示，可以看到，采用简化模型与采用有限元模型结构结果几乎没有误差。

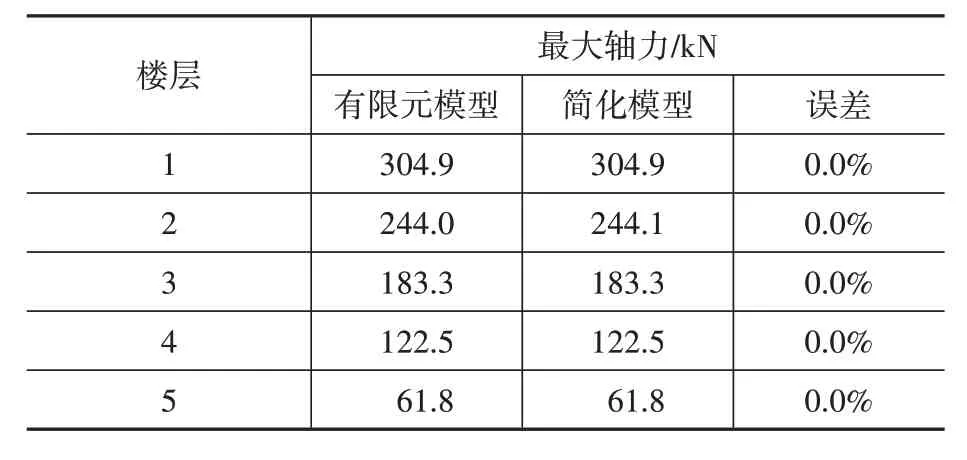
表6 竖向荷载下竖向边缘构件内力对比Table 6 Comparison of internal forces of vertical edge members under vertical load

4.3.2 非边缘构件内力

取轴①框架柱及轴①、轴②框架梁，内力对比如表7、表8所示，简化模型误差在1%以内。

综上，在各方向荷载作用下，在钢框架-无屈曲波纹钢板剪力墙结构中采用本文提出的简化分析模型具有良好的精度。

表7 竖向荷载下框架柱内力对比Table 7 Comparison of internal forces of frame columns under vertical loads

表8 竖向荷载下水平边缘构件内力对比Table 8 Comparison of internal forces of horizontal edge members under vertical load

5 结 论

本文根据波纹钢板墙的受力特性提出了多种基于连接单元的简化模型，并优选出了轴向连接单元模型作为简化分析模型，优化了简化分析模型参数，评估了简化模型对波纹钢板墙的模拟效果，并对简化分析模型在钢框架-无屈曲波纹钢板剪力墙结构分析中的适用性进行了研究，结论如下：

（1）相比于其他简化模型，轴向连接单元模型的受力模式与波纹墙更接近，传力路径直接，概念清晰。

（2）轴向连接单元模型中轴向连接单元距顶部高度h应取0.6H；采用该参数情况下，更改墙体厚度、高宽比、边缘构件刚度等参数时，该简化模型对波纹墙的抗侧刚度模拟误差在6%以内。

（3）采用轴向连接单元模型模拟钢框架-无屈曲波纹钢板剪力墙结构中波纹墙时，在各向荷载作用下，简化模型均能很好地反映结构刚度，且对非边缘构件的内力影响较小；边缘构件内力通过本文提出的公式修正后可满足精度要求。