轻钢套筒连接节点的性能研究

尹昌磊 谢 群 王 倩 朱崇绩 杨涛春，*

（1.济南大学土木建筑学院，济南250022；2.山东乾元泽孚科技股份有限公司，济南250022）

0 引 言

在近年来的地震灾害中，许多钢结构建筑的倒塌破坏均是源于框架节点的脆性断裂［1-2］。节点的抗震性能与整个建筑物的安全性密切相关，因此，设计一种合理的连接形式变得尤为重要。随着研究的深入，钢套筒连接节点应运而生，针对这一连接形式，相关专家开始对其力学性能展开研究。

刘坚、高奎等［3］提出外套管式钢管混凝土柱与钢梁单边螺栓连接节点，通过拟静力试验，对其力学性能展开研究。朱赢［4］推导出外套管式节点的弯矩—转角关系以及节点承载力计算公式。李奕生［5］提出一种新型分离式外套筒连接节点，通过建立不同尺寸的有限元模型，研究不同参数对该新型节点力学性能的影响。刘伟［6］总结了最小套筒公式，并对新型分离式套筒节点的构造提出设计建议。但国内外针对装配式钢套筒连接节点研究较少，基于已有研究，本文提出一种新型轻钢套筒连接节点，节点构造详图见图1。通过ABAQUS 有限元模拟，对新型轻钢套筒连接节点的力学性能进行分析，同时为该节点的推广应用提出设计建议。

1 模型的建立与验证

1.1 模型概况

以钢框架中T 形边节点为研究对象，梁柱截面均为矩形，其中方钢管柱截面尺寸为200 mm×200 mm×8 mm，方钢管梁截面尺寸为150 mm×150 mm×8 mm。具体尺寸见图1。

图1 轻钢套筒连接节点构造详图（单位：mm）Fig.1 Detail construction of light steel sleeve joint（Unit：mm）

1.2 材料的本构模型及网格划分

为更加真实的模拟钢材的受力特性，采用三折线本构模型，如图2 所示。螺栓也同样采用三折线模型，但不考虑下降段的影响。钢材材料参数取值［7］如表1所示。

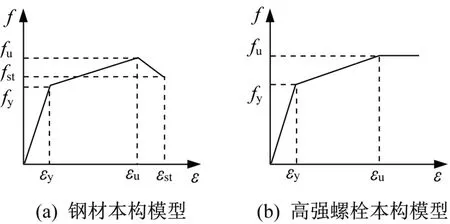
图2 材料本构模型Fig.2 Material constitutive model

模型网格划分时，采用C3D8R 线性减缩积分实体单元。为同时兼顾计算精度及计算速度，对于梁柱节点核心区及重点研究部位应该细化网格，非关键部分应粗化网格。通过试算，最终确定的网格尺寸为：套筒、螺栓以及梁柱伸入套筒内部分网格均取15 mm，其他部位网格取30 mm，如图3所示。

图3 梁网格划分图Fig.3 Beam meshing diagram

1.3 加载制度

通过查阅相关文献资料［9-10］，为保证加载过程的稳定性，采用位移控制加载，具体加载方式如下：利用有限元软件，对试件施加单向位移荷载，模拟完成后，根据荷载—位移曲线估算屈服位移Δy，以屈服位移Δy为一个步长，按照 ±Δy/2，±Δy，±2Δy，±3Δy，±4Δy的加载历程进行循环加载，其中±Δy/2，±Δy级荷载循环一次，其他级荷载循环两次，模型的具体加载设置与加载制度如图4所示。

表1 钢材材料参数取值Table 1 Steel material parameter values

1.4 模型验证

为验证有限元模型建立的准确性，需要将有限元计算的内力大小与理论值进行对比。当P=28.3 kN 时，X=0.13 m 处梁截面的模拟弯矩M1=38.83 kN·m，模拟剪力V1=28.85 kN，理论计算结果为：梁在节点处的弯矩M2=28.3×1.37=38.77 kN·m，剪力V2=28.3 kN。

有限元模拟与理论值误差的计算公式：弯矩：

剪力：

图4 位移加载曲线Fig.4 Displacement loading curve

为提高对比的准确性，对比分析了P=28.3 kN、P=40 kN以及P=50 kN三组数据，结果如表2所示。

表2 结果对比Table 2 Results comparison

通过对比以上3 组数据可知，有限元模拟结果与理论计算结果相似，误差控制在1.2%以内，由此证明轻钢套筒连接节点有限元模型合理可靠，可以用此有限元模型模拟轻钢套筒连接节点的力学性能。

2 力学性能研究

建立轻钢套筒连接节点Base 标准试件以及相同尺寸的纯刚接节点N-0 试件有限元模型，具体尺寸见表5。通过对比有限元计算结果，分析轻钢套筒连接节点的应力分布状况以及破坏机理，为轻钢套筒连接节点的设计与应用提供建议。

天气渐渐的热了起来，毕竟是三伏天，时近晌午，已经闷热难挡，吹来的风中也夹带着一篷篷的热气，红琴红衬衣上的纽扣又解开了几颗，她不时地撩起衣角，朝头上扇几下凉风。她身子略微往前倾，低着头一步一步地往岭上移动。不经意间抬起头来，蓦然发现幽静的山湾里有一泓清泉，银亮的瀑布从峭壁上垂挂下来，她一阵欢呼雀跃后，当机立断冲进瀑布底下去冲个凉。她想这次去见风影，自己理应洗得清爽一点，无论如何要再好好地洗个澡，她自认为这样做了之后自己还是一个比较干净的人，于是去洗浴的念头更强烈了，决心也更大了。她的动作很快，脑子里的念想还在飞快地打转，身子已经飞进瀑布底下，浸泡在一潭翡翠绿的水潭之中了。

2.1 破坏过程分析

应力云图如图5 所示，其中40 mm、80 mm、120 mm 分别代表边节点、梁套筒及加劲肋的梁端位移大小。

当梁端位移达到 40 mm 时，如图 5（a）所示，此时应力主要分布在远离柱侧的梁套筒上下翼缘与方钢管梁相交处，荷载作用下，梁侧壁受对拉螺栓的影响也存在一定的应力，柱套筒的应力相对较小。当梁端位移达到80 mm 时，如图5（b）所示，进入弹塑性阶段，靠近柱侧的梁套筒上下翼缘及螺栓孔的应力明显提高，并逐步向梁套筒侧壁延伸；柱套筒应力逐渐增加，加劲肋局部出现屈服。梁端位移达到120 mm时，试件局部有破坏的迹象，如图5（c）所示，远离柱侧的梁套筒边缘与方钢管梁相交处达到极限强度，此处的方钢管梁下翼缘出现挤压破坏，远离柱侧的梁套筒上翼缘螺栓孔出现局部受拉破坏，加劲肋下翼缘发生局部屈曲。

图5 应力云图Fig.5 Stress nephogram

加载过程中，Base 试件的破坏形式主要是远离柱侧的梁套筒上翼缘螺栓孔受拉破坏以及与梁套筒相交的方钢管梁下翼缘挤压破坏。在远离柱侧的梁套筒边缘与方钢管梁相交处产生塑性铰，保证了梁柱套筒连接节点的安全可靠。

2.2 套筒节点与纯刚节点的对比分析

骨架曲线反映结构整体的受力性能，如图6所示，由骨架曲线可以得到试件的具体力学特征，计算结果见表3。通过分析骨架曲线和表3 数据可知，Base 试件的初始刚度大于N-0 试件，但延性有所降低。在相同位移情况下，Base 试件的骨架曲线均比N-0试件高，说明轻钢套筒连接节点的承载力高于纯刚接节点。达到最大位移荷载后，Base试件的骨架曲线下降较快，这是由于Base 试件在3Δy荷载作用下远离柱侧的梁套筒上翼缘螺栓孔受拉破坏，承载力下降，而纯刚接节点N-0 试件结构完整性较好，在荷载作用下承载力下降缓慢。

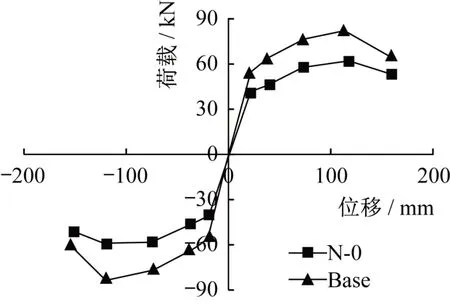
图6 骨架曲线Fig.6 Skeleton curve

表3 试件初始刚度与承载力Table 3 Intitial stiffness and bearing copacty

结构的耗能能力可以通过计算等效黏滞阻尼系数he来衡量，等效黏滞阻尼系数越大，结构的耗能能力越强［11］。等效黏滞阻尼系数he的计算公式如下：

通过计算，试件的等效黏滞阻尼系数he见表4。由表中数据可知，在Δy、2Δy荷载作用下，Base试件与N-0 试件相比其等效黏滞阻尼系数he更大，在3Δy荷载作用下，Base 试件的等效黏滞阻尼系数he略小于N-0 试件，这是由于Base 试件中梁套筒上翼缘螺栓孔被拉坏以及与梁套筒相交的方钢管梁下翼缘发生挤压破坏，试件承载力下降，消耗动能的能力减弱。

表4 等效黏滞阻尼系数Table 4 Equivalent viscous damping coefficient

通过以上分析可知，轻钢套筒连接节点的强度和刚度均高于纯刚接节点，耗能能力相对更好，力学性能明显优于相同截面尺寸的纯刚接节点。

3 参数分析

根据套筒壁厚、梁柱壁厚以及套筒外伸长度三个参数，建立7 种不同尺寸的轻钢套筒连接节点有限元模型，研究不同参数对轻钢套筒连接节点力学性能的影响。试件编号及尺寸见表5。

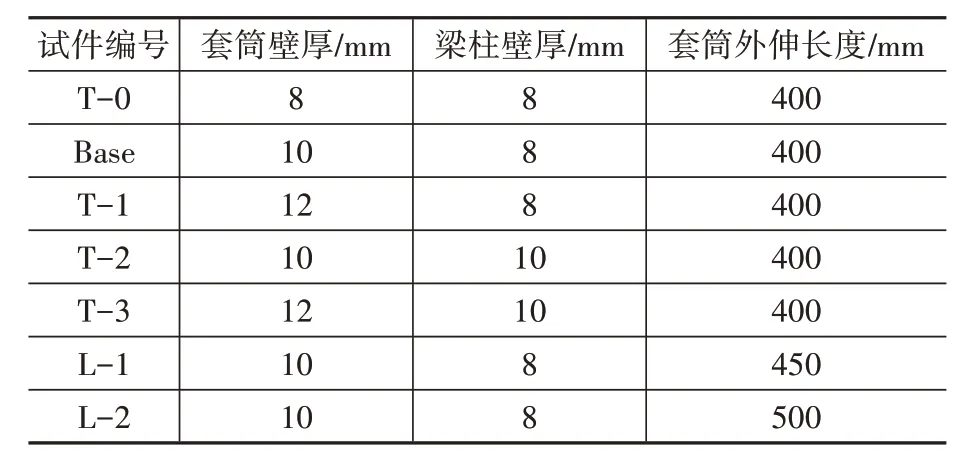
表5 试件编号及尺寸Table 5 Test piece number and sizes

3.1 套筒壁厚对节点力学性能的影响

通过分析骨架曲线及表6 数据可知，在相同位移情况下，Base 试件和T-1 试件的初始刚度及屈服位移均高于T-0 试件，说明试件的承载力随着套筒壁厚的增加而提高。继续增加荷载至破坏阶段，可以发现T-1 试件骨架曲线下降幅度较大，这是因为套筒壁厚增加，节点刚度增大，延性降低，试件提前破坏。

表6 试件初始刚度与承载力Table 6 Initial stiffness and bearing capacity

试件的等效黏滞阻尼系数见表7。分析表中数据可知，T-0 试件、Base 试件与 T-1 试件的等效黏滞阻尼系数he均随着外荷载的增加而逐渐增大。在Δy，2Δy荷载作用下，等效黏滞阻尼系数he随着外套筒壁厚的增加而逐渐增大；当荷载达到3Δy时，试件的等效黏滞阻尼系数he随着套筒壁厚的增加而降低。

表7 试件等效黏滞阻尼系数Table 7 Equivalent viscous damping coefficient

通过以上分析可知，随着套筒壁厚的增加，试件承载力明显提高，当外套筒壁厚超出一定范围以后，试件的初始刚度和屈服承载力提高，延性降低，极限承载力降低，变形能力及耗能能力减弱。因此，建议套筒壁比梁壁厚2 mm。

图7 骨架曲线Fig.7 Skeleton curves

3.2 梁厚对节点力学性能的影响

通过分析图8 骨架曲线及表9 数据可知，T-3试件的初始刚度、屈服承载力以及极限承载力较T-1 试件均有明显提高，进入弹塑性阶段后，T-1试件的承载能力随着位移的增加而大幅度下降，这是由于T-1 试件的梁壁厚与套筒壁厚相差较大，未完全发挥套筒作用梁端便发生破坏；对比分析Base 试件与T-2 试件可知，试件的承载能力随着梁厚的增加而逐渐提高，由于T-2 试件的套筒壁与梁壁厚度一致，增加荷载至破坏阶段时，T-2试件将在节点处发生破坏，而Base 试件则在与梁套筒相交的方钢管梁处破坏，节点处的整体性较好，所以T-2 试件的骨架曲线下降段显得更平缓，延性更好。

表8 试件等效黏滞阻尼系数Table 8 Equivalent viscous damping coefficient

图8 骨架曲线Fig.8 Skeleton curves

试件的等效黏滞阻尼系数he见表8。分析表中数据可知，Base 试件、T-1 试件、T-2 试件与 T-3试件的等效黏滞阻尼系数he均随着外荷载的增加而逐渐增大，耗能能力较好。对比分析Base 试件与T-2 试件可知，当增加梁壁厚度至与套筒壁厚度一样时，等效黏滞阻尼系数he增长不明显。对比分析 T-1 试件与 T-3 试件可知，在 2Δy、3Δy荷载作用下，T-3 试件的等效黏滞阻尼系数大于T-1试件。

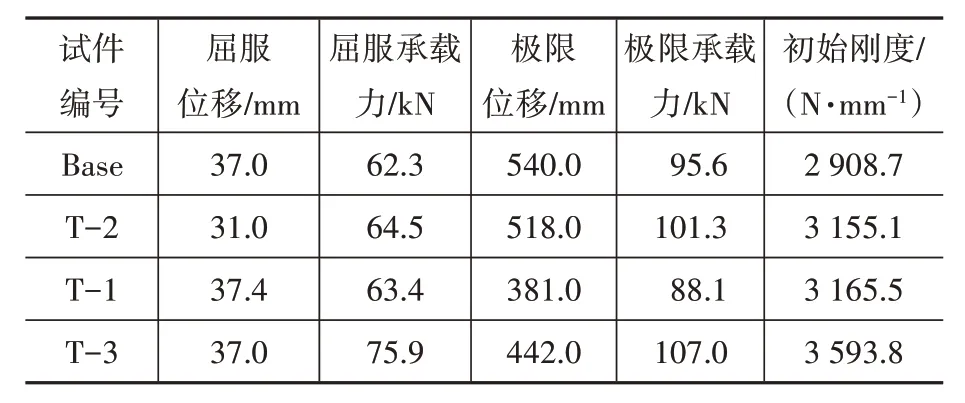
表9 试件初始刚度及承载力Table 9 Initial stiffness and bearing capacity

由此可见，随着梁壁厚度的增加，试件的承载力及耗能能力均显著增强；当梁厚和套筒壁厚一致时，刚度提高，转动能力减弱，破坏形式发生转变。因此，梁壁比套筒壁薄2 mm时为最佳。

3.3 套筒长度对节点力学性能的影响

通过分析图9 骨架曲线及表10 数据可知，Base，L-1 及L-2 试件的初始刚度相差不大，但L-1试件的极限承载力随着外荷载的增加而显著提高。三个试件的承载力均随着套筒外伸长度的增加而提高，继续增加荷载至破坏阶段，可以发现L-2 试件相比Base 试件和L-1 试件其骨架曲线下降得较为平缓，这是由于Base 试件与L-1 试件均在远离柱端的梁套筒上翼缘螺栓孔处受拉破坏，承载力下降较快。

图9 骨架曲线Fig.9 Skeleton curves

试件的等效黏滞阻尼系数he见表11。Base、L-1 和L-2 试件的等效黏滞阻尼系数he均随着外荷载的增加而逐渐增大，三个试件消耗动能的能力较好。在各级荷载作用下，Base 试件和L-1 试件的等效黏滞阻尼系数he均小于L-1试件。

表10 试件初始刚度及承载力Table 10 Initial stiffness and bearing capacity

表11 试件等效粘滞阻尼系数Table 11 Initial stiffness and bearing capacity coefficient

由此可见，试件的承载力及耗能能力随着套筒外伸长度的增加而提高，当套筒外伸长度超出一定范围后，节点刚度增加，破坏形式发生转变，试件会在节点加劲肋处发生破坏，承载力下降。

4 结 论

（1）轻钢套筒连接节点Base试件与等截面尺寸的纯刚接节点N-0 试件相比，其初始刚度和承载力均有明显提高。两者的滞回曲线和骨架曲线形状相似，但轻钢套筒连接节点的耗能能力更加优异。

（2）随着外套筒壁厚的增加，试件的初始刚度以及极限承载力均大幅度提高，耗能能力增强，当套筒壁厚超出一定范围以后，初始刚度提高，延性降低，试件的耗能能力减弱，承载力下降。因此，套筒壁比梁壁厚2 mm时为最佳。

（3）随着梁壁厚度的增加，试件的承载力及耗能能力均显著增强。当梁厚和套筒壁厚一致时，刚度提高，破坏形式转变为节点域破坏，不符合“强节点弱构件”的抗震设计理念。因此，梁壁比套筒壁薄2 mm时为最佳。

（4）随着套筒外伸长度的增加，试件的承载力及耗能能力均显著增强，当套筒外伸长度超出一定范围以后，破坏形式转变为节点域破坏。