雷达通信干扰一体化OFDM共享波形优化方法
2020-12-16朱晟坤杨瑞娟左家骏李东瑾
朱晟坤,杨瑞娟,左家骏,李东瑾
(空军预警学院, 武汉 430000)
随着电子信息技术的发展和信息化作战需要,作战平台上需要装备诸如雷达、通信和干扰等复杂的电子系统,这在增强信息作战能力的同时,也削弱了作战平台的机动性,且不同设备之间会产生严重的电磁干扰。而多功能电子系统的一体化是解决上述问题的有效途径。近年来的研究表明雷达和通信可以通过共享信号实现高度一体化。这种雷达通信一体化共享信号携带通信数据,接收端通过解调提取通信信息,并经过雷达信号接收处理提取目标信息[1]。干扰是通过发射特定干扰信号破坏敌雷达、通信等电子设备正常工作的功能。在上述基于共享信号的雷达通信一体化系统中,通过合理的信号波形设计,一体化共享信号还可用作为干扰信号,从而实现雷达通信干扰一体化。通过波形优化设计,基于共享信号的雷达通信干扰一体化系统可以根据实际需要,优化调整参数,从而达到最优效能。这种建立在共享信号基础上的雷达、通信、干扰一体化是一种未来的发展方向[2]。
近年来,国内外学者研究了诸多雷达通信一体化共享信号的方法[3-6]。正交频分复用(OFDM)是一种具有良好的抗多径衰落的高速数据通信调制技术。由于它具有宽频带、频谱利用率高、抗多径干扰能力强等优点,OFDM成为雷达通信一体化共享信号研究热点[7-9]。针对OFDM体制的一体化共享信号技术,围绕雷达通信一体化波形设计、雷达接收信号处理和系统性能分析等方面,业内开展了大量研究,并取得了丰硕成果[10-11]。在波形优化方面,前期的研究主要针对雷达通信共享波形优化。文献[12]提出以最大化条件互信息为目标函数优化发射波形。文献[13]的研究表明,最小化目标均方误差在估计目标脉冲响应中等同于最大化条件互信息。文献[14]提出了一种通信信息预调制的方法,来消除加载通信信息对雷达模糊函数的影响。文献[15] 基于凸优化提出了一种以雷达条件互信息和通信数据率为目标函数的优化方法。目前,针对加入干扰的一体化共享波形优化的研究较少。文献[16]提出了一种基于间歇采样倒序填充的干扰方法,用以生成前导假目标。文献[17]提出用噪声卷积和射频噪声干扰共享信号的方法,分析了噪声卷积干扰和射频噪声干扰对DS-CSS共享信号目标探测与通信功能的干扰效果。但文章只研究了共享信号的抗干扰能力,并未研究共享信号的干扰能力。加入干扰功能后,雷达、通信、干扰共享波形应如何优化配置资源,使得三者同时作用时的综合性能最优,还需要进一步研究。
本文针对OFDM共享信号的雷达、通信、干扰一体化,提出了一种雷达、通信、干扰一体化共享波形的优化方法。在雷达条件互信息、通信数据信息率、干扰熵值等目标函数的基础上,建立了分配权重的一体化目标函数,并基于遗传算法实现一体化目标函数下的OFDM共享信号子载波功率优化,可为雷达通信干扰一体化应用提供理论参考。
1 问题描述与建模
基于OFDM的雷达通信干扰一体化共享信号波形优化的目的是在尽可能少地损失雷达通信性能的前提下,提高共享信号的干扰能力。本文的思路是:首先分别针对雷达、通信、干扰建立单目标函数,可采取传统的注水法求得单目标函数下的雷达、通信、干扰最优解。然后考虑雷达、通信、干扰一体化作用时的综合性能优化,为3个目标函数分配权重,建立一体化目标函数,并运用遗传算法对优化问题求解。
1.1 OFDM信号模型
OFDM信号波形可以描述为[18]:
(1)
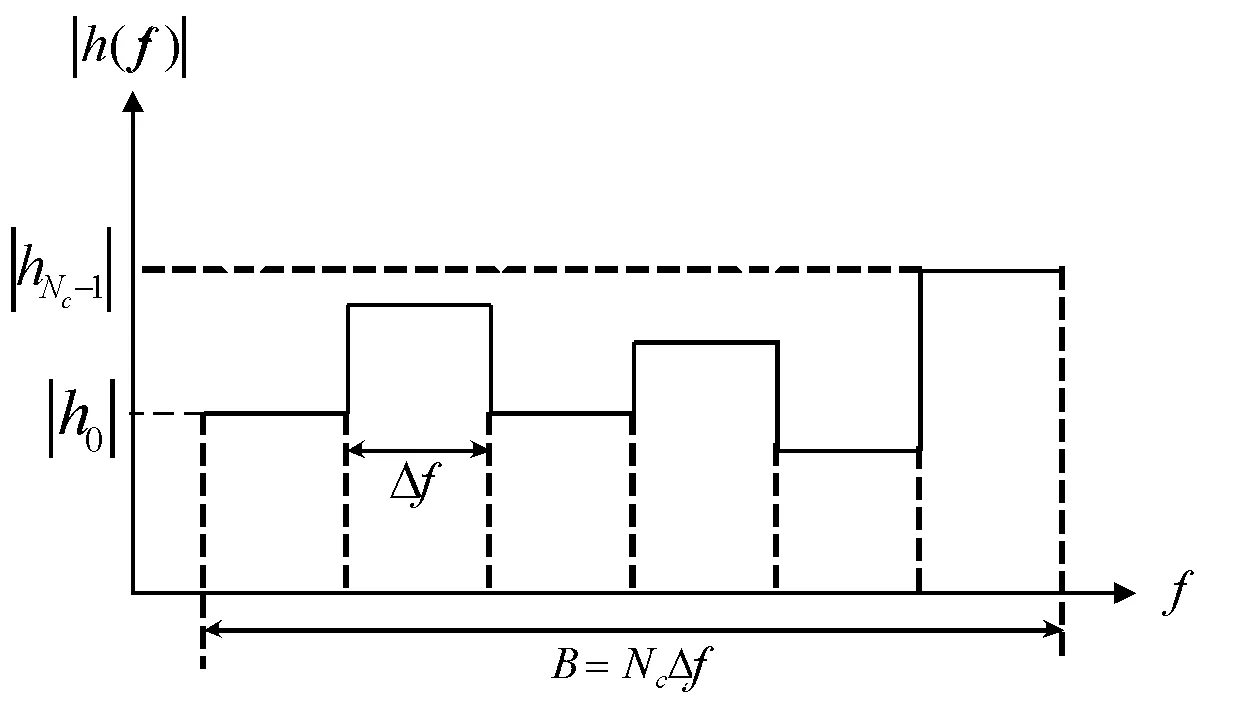
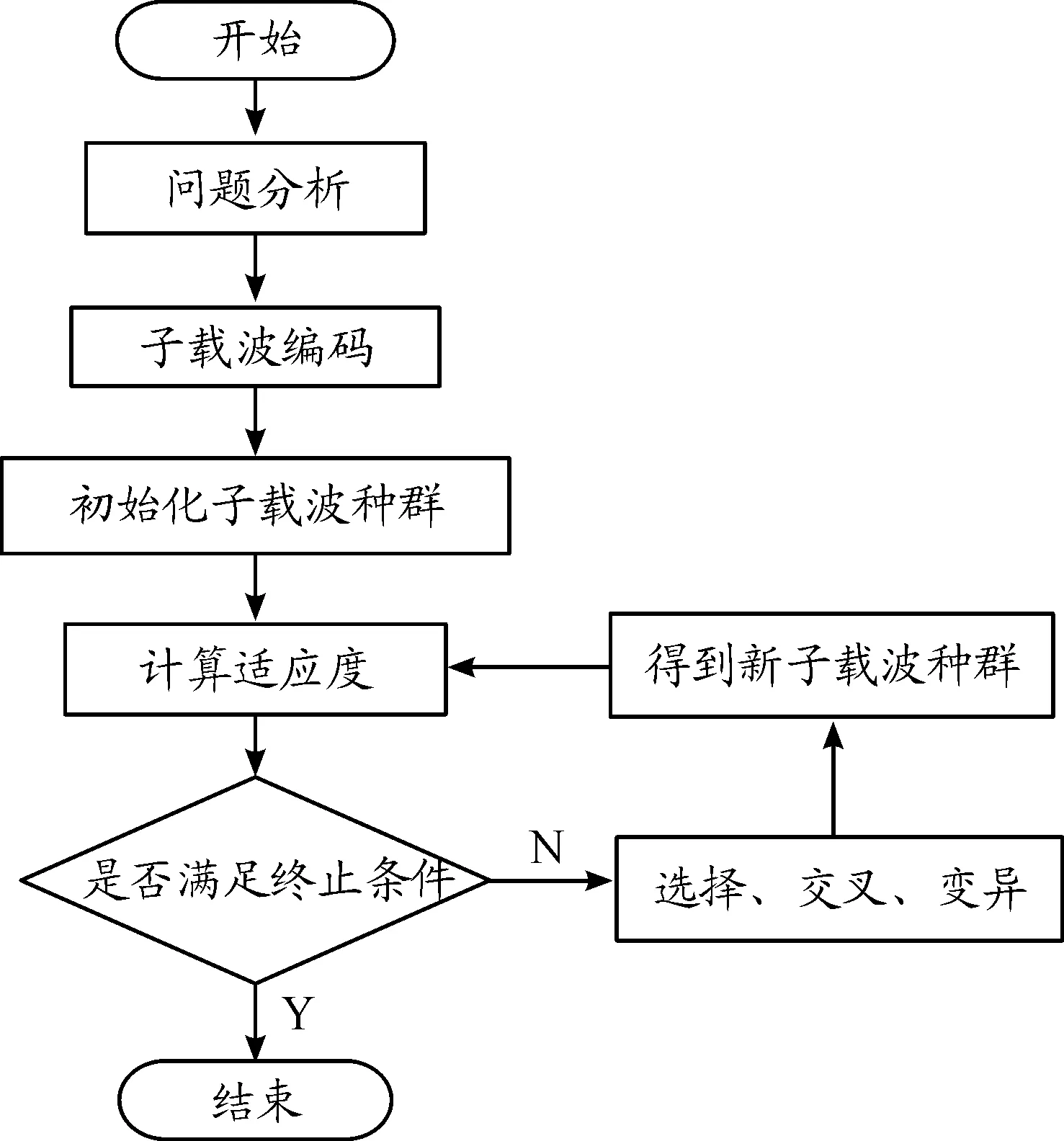
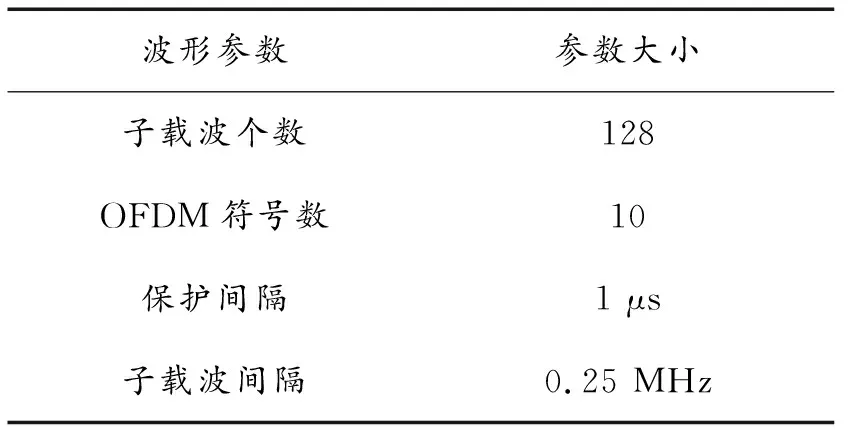
其中:fc为信号的中心频率;Ns为OFDM符号数;Nc为子载波个数;am为信号的幅度;cm,n为第m个子载波的相位编码; Δf=1/T,T为每个OFDM符号的持续时间间隔;Ts为完成每个OFDM符号的时间间隔,Ts=T+Tg,其中Tg是每个循环前缀的持续时间;rect[t/Ts]为矩形函数,0 条件互信息对于雷达目标的识别和分类,具有十分重要的数学意义,为了提高目标冲激响应估计精度,就需要最大化条件互信息。 假设目标的冲激响应g(t)为高斯随机过程,那么接收到的回波y(t)为[15] (2) 其中,n(t)为零均值的高斯白噪声。 目标脉冲响应和接收信号之间的条件互信息为 I[y(t);g(t)|s(t)]= (3) 其中:S(fm)、G(fm)和N(fm)分别为s(t)、g(t)和n(t)的傅里叶变换;在频率间隔Θm=[fm,fm+1]之间,假设S(f)≈S(fm),G(f)≈G(fm),N(f)≈N(fm),其中fm=fc+mΔf为第m个子载波的中心频率;Tp=Ns·Ts为信号周期。 定义Q(f)=|S(f)|2,则可得到如下等式: e-j2π(f-fc)(n-n′)Tse-jπ(m-m′)ΔfTs· sa[π(f-fm)Ts]·sa[π(f-fm′)Ts] (4) 其中,(·)为复共轭变换,sa(t)=sint/t。 通信编码cm,n实际上是由携带的信息所决定的。通过预编码,可以使通信编码是均匀分布的随机码,则有如下等式: 其中,E[·]是期望算子。E[Q(f)]可以简化为如下等式: (6) 当Nc和Ns足够大时Q(f)的值会逼近它的均值E[Q(f)],实际上OFDM信号的子载波数有上百个,可以达到上述的约束条件,故有下式: (7) 当m≠m′时,sa(π(f-fm))Ts远远小于1,故可作如下估算: (8) (9) 在频率选择性衰落信道中,通过合理的分配改善每个子载波的发射功率可以提高通信数据信息率,假设通信信道是慢时变和频率相关的。频率衰落响应h(f)如图1所示,其概率密度函数服从瑞利分布。 在加性白噪声信道中信号数据率的模型为[19]: (10) 图1 频率衰落响应曲线 雷达检测目标要在噪声中进行,检测接收信号中有无目标的假设检验具有不确定性[20]。因此,最佳的干扰遮盖性波形就是不确定性最大的波形,而衡量随机变量不确定性的量是熵值,对连续随机变量,熵值定义为 (11) 当概率密度函数为正态分布时,熵值可化简为 (12) OFDM信号是把多个相互正交的信号相互叠加形成的,根据中心极限定理,OFDM信号概率密度接近正态分布[21]。因此,OFDM信号就是最佳遮盖性干扰波形。假设被干扰雷达频段已知,为提高干扰能力,可以将干扰频段内的熵值最大化,从而达到最佳干扰效果。式(12)中pt是分布在干扰频段内的OFDM子载波功率和。 目标函数也叫适应度函数,是遗传算法进行迭代的重要依据。在本文中,个体定义为子载波的发射功率,适应度函数是雷达条件互信息、通信数据率、干扰熵值三者带权的联合目标函数f(x),定义如下: (13) 式中:ω1、ω2、ω3分别为雷达条件互信息、通信数据率、干扰熵值赋予的权重,可根据实际情况调节,且ω1+ω2+ω3=1。F1、F2分别为式(9)、式(10)的最优解,可以通过注水法求解得到[22-23],F3为干扰功率的最大值,目的是先将各目标函数进行归一化处理,再根据具体性能要求赋予单个目标函数一定的权重。 式(13)的约束条件如下: (14) 式中Psum是OFDM信号所有子载波的功率和。 单目标函数优化求解问题可以通过注水法直接求解,但复杂的多目标问题难以通过注水法直接求解。遗传算法是一种通过模拟生物进化论的自然选择和生物进化过程的寻找最优解的算法,具有以下优点:能够求出优化问题的全局最优解、优化结果与初始条件无关、算法独立于求解域、具有较强的鲁棒性,适合于求解复杂的优化问题。故本文采用遗传算法优化求解雷达、通信、干扰一体化目标函数。 在遗传算法中,交叉、变异和选择共同构成了算法的遗传操作;编码、初始种群的设定、目标函数的设计、设计遗传操作、参数控制设定等5个要素构成了算法的核心内容[24-25]。 遗传算法是从一个问题的解集的一个种群开始的,而一个种群由经过编码的一定数量的个体组成,编码采用二进制编码。将式(13)作为适应度函数,子载波分配的功率值作为个体,并形成种群,求出种群中每一个个体的适应度,即式(13)的值。按照达尔文进化论“优胜劣汰”的原理选择出适应度高的个体,淘汰适应度低的个体后,对剩余的种群进行变异、交叉和重组,组成新的种群,再次选择出适应度高的个体。循环迭代,直至适应度达到最优,停止迭代,选择出适应度最高的个体,即为使总体效能达到最优的子载波最优功率分配方案。算法流程如图2所示。 图2 遗传算法流程框图 对应测试环境如下: 1) 初代种群即子载波功率采用随机方式产生,总功率为100; 2) 第1个子载波中心频率为0,干扰频段为0~7.5 MHz,对应OFDM信号前30个子载波,预分配功率值为50; 3) 迭代次数设置为2 000次,子载波个数设置为128,种群大小设置为80,变异概率设置为0.2,交叉概率设置为0.8。 4) 计算机配置为CPU i7-8750H,Matlab版本为R2016b。 5) OFDM信号波形参数设置如表1所示。 6) 通信信道频率选择性衰落采用瑞利分布模型。 表1 OFDM信号波形参数 下面通过雷达条件互信息性能验证遗传算法的有效性。首先在式(3)的雷达条件互信息目标函数下,通过注水法获得优化结果,再在一体化目标函数下基于遗传算法进行优化解算。如图3所示,在信噪比为20 dB时,遗传算法迭代 6 000 次时,遗传算法所得的条件互信息为1.735 5,收敛于注水法求出的最优解1.740 2,表明算法是有效且收敛的。 对系统的雷达条件互信息性能进行仿真,并将本文的方法与条件互信息和数据率等单目标函数下的注水法、等功率分配方法以及文献[15]的雷达通信一体化凸优化方法进行对比。 图4给出了一体化共享信号的雷达条件互信息随信噪比的变化曲线。显然,随着信噪比的增大,各种方法下的条件互信息均逐渐增大。其中,在式(3)条件互信息单目标函数下的注水法由于仅考虑雷达性能优化,故达到共享波形雷达条件互信息性能的上界,文献[15]和一体化目标函数下的遗传算法性能次之,由于文献[15]仅考虑雷达通信一体化性能优化,因此其雷达性能略显优势,本文算法综合考虑雷达通信干扰一体化优化,在等权重ω1=ω2=ω3=1/3时,雷达性能损失约8%,在权重ω1=ω2=0.4,ω3=0.2时,雷达性能约损失6%,在权重ω1=0.5,ω2=0.25,ω3=0.25时,雷达性能约损失4%,可见通过调整权重可改善雷达性能。其余的包括数据率等单目标函数下的注水法、等功率分配法的雷达性能均不及本文算法性能。 对系统的通信数据率性能进行仿真,并将本文的方法与条件互信息和数据率等单目标函数下的注水法、等功率分配方法以及文献[15]的雷达通信一体化凸优化方法进行对比。 图5给出了一体化共享信号的通信数据率随信噪比的变化曲线。显然,随着信噪比的增大,各种方法下的数据率均逐渐增大。其中,在式(10)数据率单目标函数下的注水法由于仅考虑通信性能优化,故达到共享波形通信数据率性能的上界,文献[15]和一体化目标函数下的遗传算法性能次之,由于文献[15]仅考虑雷达通信一体化性能优化,因此其雷达性能略显优势,本文算法综合考虑雷达通信干扰一体化优化,在等权重ω1=ω2=ω3=1/3时,通信性能损失约10%,在权重ω1=ω2=0.4,ω3=0.2时,通信性能约损失8%,在权重ω2=0.5,ω1=0.25,ω3=0.25时,通信性能约损失6%,可见通过调整权重可改善通信性能。其余的包括条件互信息等单目标函数下的注水法、等功率分配法的通信性能均不及本文算法性能。 图5 通信数据率曲线 图6给出了被干扰雷达的ROC曲线。从图中可以得知,一体化目标函数下,本文的基于遗传算法的优化波形有效的降低了敌方雷达的检测概率,其干扰性能相较于文献[15]和等功率分配均有显著提升,并从图中可以得出,当提高干扰熵值目标函数权重后,干扰效果提升十分显著,表明本文方法在提升雷达通信干扰一体化性能方面表现良好。 图6 ROC曲线 一体化目标函数的权重体现了一体化共享波形资源分配方案,也决定了雷达、通信、干扰三者的性能。用帕累托(Pareto)前沿[26]来反映在不同权重下的优化方案,Pareto前沿是一体化目标函数的最优解集合的图形化表示,如图7所示,图7中的横纵竖坐标分别为最优共享波形的归一化条件互信息、数据率和熵值,图中每一点都对应该一体化目标函数的最大值。图7显示了信噪比20 dB条件下的Pareto前沿。 图7 一体化目标函数的Pareto前沿图 图7中各点均使得一体化目标函数达到最优,但其权重各不相同,所获得的雷达、通信、干扰性能也不相同。图7中的五角星分别对应了权重为ω1=1,ω2=ω3=0、ω1=ω3=0,ω2=1和ω1=ω2=0,ω3=1,即表示一体化共享信号波形资源面向雷达、通信或干扰等单一功能分配时的性能。因此,一体化系统可以根据实际需求在雷达、通信、干扰性能中做出权衡,优化加权系数,使得一体化目标函数保持最优。 基于OFDM的雷达、通信和干扰一体化共享波形优化方法,给出了一体化目标函数在总功率一定的约束下,基于遗传算法的雷达、通信、干扰一体化共享波形优化方法,在损失少部分雷达和通信性能信息的前提下,能够使OFDM信号获得较强的干扰能力,使雷达通信干扰一体化性能最优。本文优化方法能够根据雷达、通信、干扰性能需求,通过优化权重配置,使一体化系统总体性能保持最优,对实际应用具有重要理论参考价值。1.2 雷达条件互信息目标函数
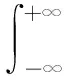
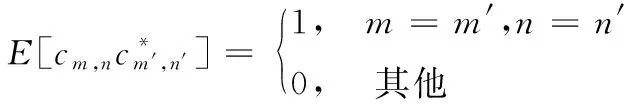
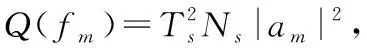
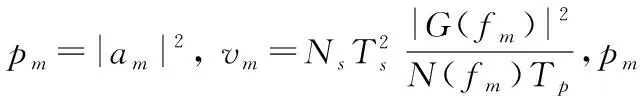
1.3 通信数据率目标函数
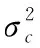
1.4 干扰熵值目标函数

1.5 一体化目标函数
2 基于遗传算法的波形优化方法
3 仿真性能分析
3.1 算法的有效性
3.2 雷达性能分析
3.3 通信性能分析
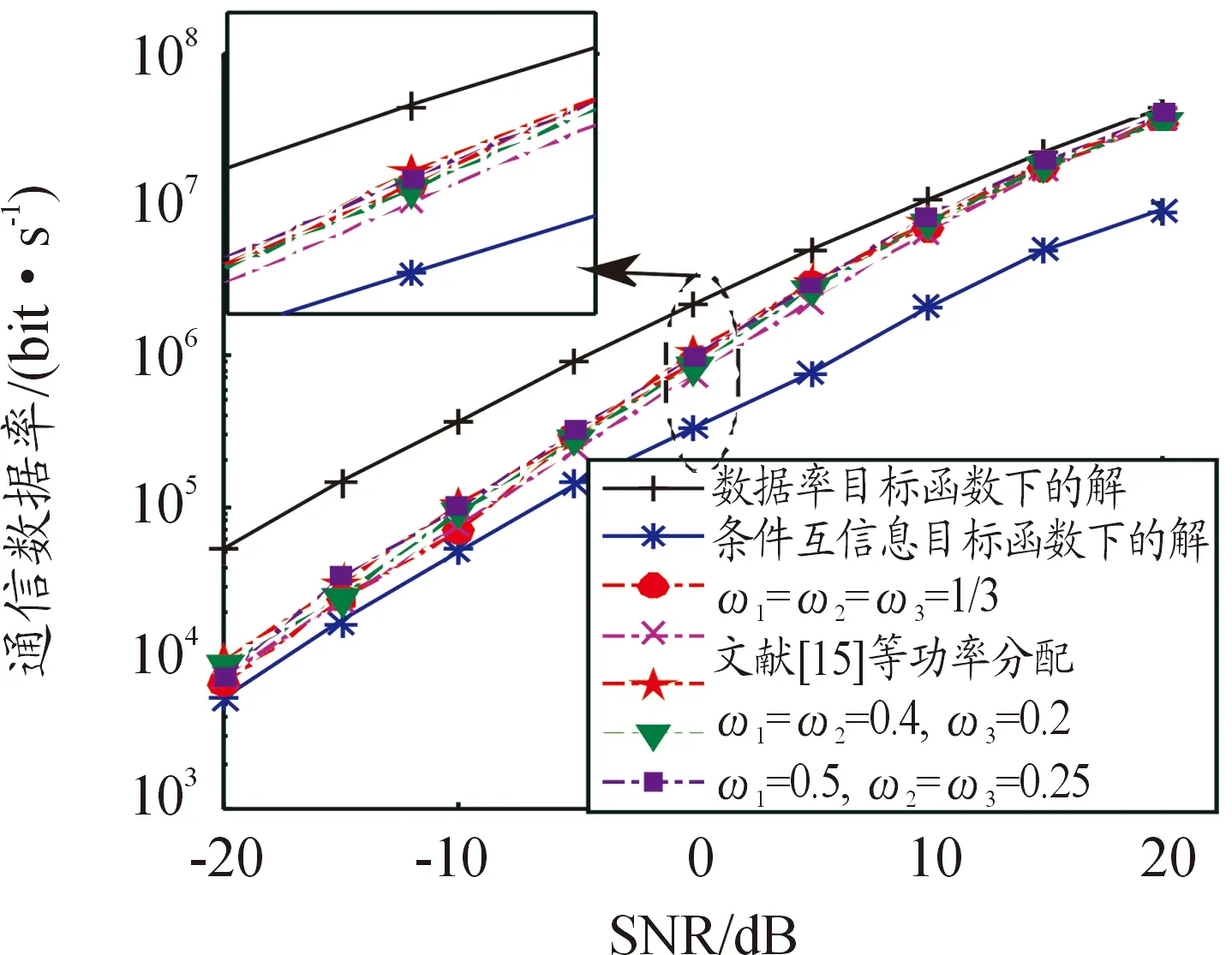
3.4 干扰性能分析
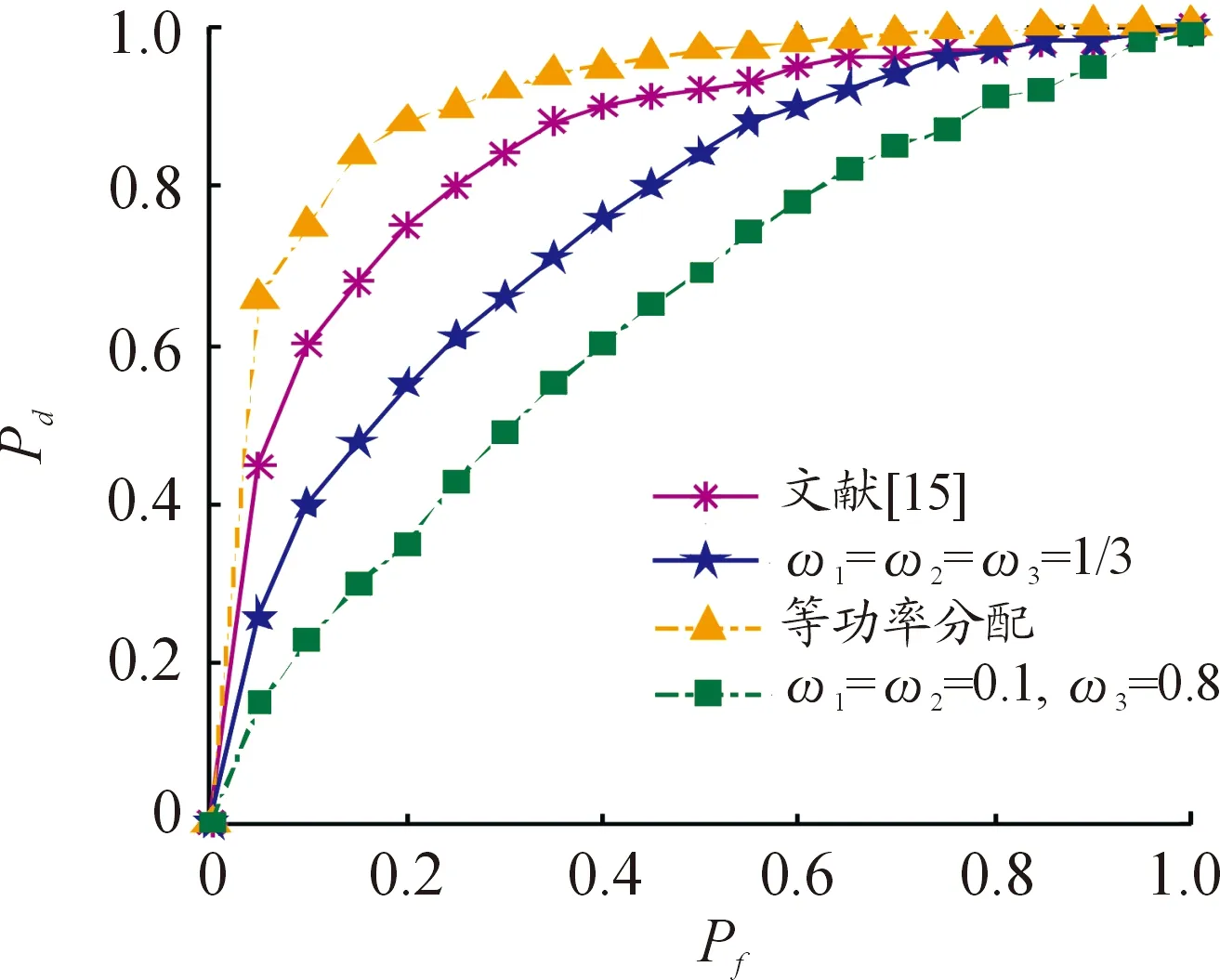
3.5 权重优化
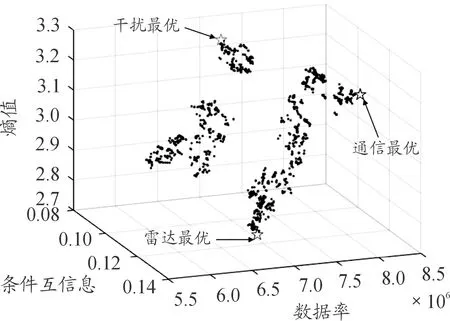
4 结论
