基于全局最优变换矩阵的图像拼接方法

孙商文，刘 宇，徐昭洪，王昱峰

(空军航空大学 数字地球实验室， 长春 130000)

受限于相机视角小、画幅小的现状，想要获取高分辨率大场景的全景图像具有一定难度，需要将获取的多张具有重叠区域的高分辨率图像拼接成一幅全景图像。目前，图像拼接技术已经成为计算机图形学的研究焦点，被广泛应用于空间探测、遥感图像处理等领域。图像拼接一般主要分为3个过程：特征点的检测与匹配、基于特征的图像变形、拼接缝的寻找与融合。

对成像场景接近于平面或者相机拍摄绕固定中心旋转的图像进行拼接时难度较低，主流的图像处理软件都可以获得比较理想的拼接效果，如何处理视差图像的拼接问题成为学者研究的热点。Zhang等[1]提出将单应矩阵变换与内容保护方法进行结合的方法，有效解决了视差图像的拼接问题；Lin等[2]提出一种基于缝引导的局部对齐的方法解决视差问题，首先利用特征点组生成若干局部单应变换矩阵，变形图像进行初步的配准，然后使用结构保护和特征加权对局部配准区域进行不断优化，通过评价不同的拼接缝效果，选择配准效果和拼接缝质量最好的一组结果进行拼接。Li等[3]提出一种鲁棒弹性形变的方法进行视差图像的拼接，首先使用局部自适应对齐方法消除匹配点的投影误差，再利用贝叶斯模型进行优化特征匹配，最后结合全局最优相似变换完成非重叠区域变形的过渡。樊逸清等[4]提出使用线约束的最小二乘法的视差图像拼接技术，利用逐点变换保证了变形前后特征点位置不变，并加入了线约束项，保持了结构的稳定性。齐向民等[5]提出基于细分网格进行局部区域配准并结合全局相似变换的视差图像拼接算法。

针对目前在解决视差问题中出现的重叠区域纹路复杂度高难以配准、非重叠区域的透视失真以及特征点配准误差较大产生结构变形严重等问题，本文提出一种基于最优单应矩阵的拼接方法，既考虑了单应变换保留整体结构，又引入最优拼接缝保证重叠区域重要目标保护。

1 最优全局单应矩阵的筛选

单应性矩阵是图像拼接过程中一种变换模型，这种变换模型是通过像素点与像素点之间的配对，经过某种变换关系来进行变换，然后再用求得的变换关系逆向获取矩阵。单应性矩阵可以将2个图像的框架进行粗略对齐，保证变换后的图像在结构上保持稳定，不易出现图像扭曲，而粗对齐后出现图像变形、透视失真等问题，可以通过结合最优拼接缝寻找与图像融合进行处理。

假设源图像与目标图像在重叠区域的匹配点为p=[x,y,1]T和q=[u,v,1]T，则单应性变换矩阵代表从p映射到q，其关系式如下：

q～Hp

(1)

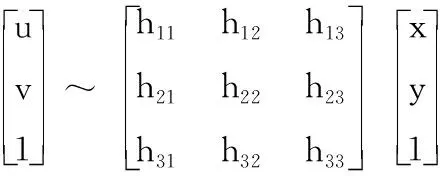
(2)

如果从两幅图像中获得4个相应的像素点，即可以获得四对匹配点，则可以生成8个线性方程，通过解算该线性方程，可以获取一个单应性矩阵H。在图像配准中，目标区域的投影平面的获取受到特征点的影响，这导致只有少数区域在图像配准后可以对齐，本文提出的最优单应性矩阵获取由最小化配准误差和分析特征点分布来进行筛选。

为了获得一组鲁棒特征点集，在输入图像I1和I2中使用SIFT算法来进行提取特征点，特征描述符用来确认在重叠区域的匹配对pi=(x,y)和qi=(u,v)的信息，最优单应性矩阵基于这些匹配点进行选择,具体步骤如下所述：

步骤1随机选取4组匹配点来进行计算单应性矩阵，判断剩下的匹配点是否满足该单应性矩阵。如果匹配点满足该矩阵，为每个点设置一个计数值来标记满足次数。计算配准误差Ri的总和，并使用内点集来更新单应性矩阵。

步骤2如果计数值大于所有特征点的平均计数值的k倍，则将这些特征点设置为无效，根据经验将k设置为3；有效特征点的总数记做Ni；同时更新内点集。否则，转到步骤1；同时，如果所有匹配点的平均计数值都大于n，根据经验n设置为2.15，则停止迭代过程。否则，转到步骤3。

步骤3判断Ni是否小于ε×N，如果满足，添加单应性矩阵到候选单应性矩阵集中，否则放弃该单应性矩阵；(设置ε为0.15，N代表所有匹配点的数目)

步骤4在获得多个候选单应性矩阵后，计算每个候选矩阵中特征点之间的欧式距离，标记为Si，结合步骤1计算的特征点之间的配准误差Ri，则最佳单应性矩阵结合 max(Si/Ni) 和min(Ri/Ni)来进行选择。

2 对齐优化模型

2.1 全局最优相似变换

为了解决在非重叠区域产生的透视失真问题，引入全局相似变换来平滑过渡透视变换到非重叠区域。全局相似变换可以近似摄像机在目标图像和参考图像之间的运动，可用于补偿相机运动。但是，使用所有匹配点来寻找全局相似变换矩阵会导致所获取的矩阵不是最佳结果，尤其是当重叠区域包含不同的图像平面时。

在获得特征点匹配后，首先使用带有阈值εg的RANSAC算法移除异常值，保留最佳匹配点。然后，使用阈值εl来查找具有最大内点的单应性平面，其中εl<εg，并且删除内点，重复直到内点的数量小于n。

(3)

每组匹配的内点用于计算单个相似转换Si，然后获得相应转换的旋转角ti，其中最小的旋转角所对应的转换矩阵为最佳相似转换矩阵S。

计算完全局相似变换后，用它调整目标图像的扭曲以减轻全景图中的透视变形。采用平滑外推的方法，

Ht=μHH+μsHs

(4)

Hr=HtH-1

(5)

式中：H为全局最优矩阵变换函数；Hs为全局最优相似变换函数；μh和μs为加权系数，并约束μh+μs=1，其中μh和μs线性变化于0～1。系数的计算方式根据AANAP[6]中提供的方法。

(6)

2.2 最优拼接缝

最优拼接缝方法假设在拼接图像的重叠区域存在一条最小差异的路径，选用合适的算法，从上而下遍历路径两侧的像素值，取得一条差异最小的路径，其中选择合适的能量函数尤为重要，对拼接缝选择的质量有着决定作用，并影响最终拼接效果。Duplaquet[7]提出的最佳缝合线算法需要同时满足颜色差异最小化和结构差异最小化，即

(7)

(8)

(9)

其中：λ为权值系数;Ecolor(x,y)为图像的颜色差异强度值；a(x,y) 为灰度值；V为像素点周围的矩形区域；Nv为区域内的像素点个数；Egeometry(x,y)为图像结构差异强度值;Sx和Sy为3×3的Sobel算子模板；I1(x,y)和I2(x,y)为待拼接图像灰度值。

Sobel算子只能对水平和垂直方向进行计算没有考虑周围方向的信息，文献[8]改进了Sobel算子进行8个方向的计算，同时在向下遍历像素时，应考虑水平方向像素值的影响，所以在重叠区域遍历像素时，除左右边界像素点只对3个方向进行检测，其他像素点从5个方向进行检测，将计算得到的准则值最小的点作为备选拼接点，按照由上至下进行，直到最后一行结束。改进后的计算公式如下：

(10)

其中：i为第几条拼接线；ω为拼接线总数；n为该拼接线的像素点个数；L为拼接线长度；Ec为灰度值之差；Eg为结构值之差，

Ec(xk,yk)=|I1(xk,yk)-I2(xk,yk)|

(11)

(12)

gj(x,y)=(I1(x,y)-I2(x,y))×Sj，j∈[1,8]

(13)

其中：I(x,y)为坐标(x,y)的灰度值；g(x,y)为(x,y)的梯度值；Sj为8个方向的Sobel算子。

Emin=min(E1,E2,…,Ei)

(14)

能量值最小的Emin所代表的拼接线为最优拼接线。

3 基于最优矩阵的拼接算法

利用全局最优单应性矩阵和全局最优相似矩阵实现输入图像的框架对齐，保持源图像的结构，再利用最优拼接缝搜索算法寻找能量最小拼接缝，解决光照不均、重要目标保护等问题，最后采用加权方式进行图像融合。据此，提出了一种新的视差图像的拼接算法，步骤如下：

1) 检测输入图像I1和I2的SIFT特征点，利用特征点的分布情况和最小化配准误差筛选出最佳全局单应性矩阵；

2) 使用带有阈值εg的RANSAC移除异常值。然后，使用阈值εl查找具有最大数量内点的单应性矩阵，每组匹配的内点用于计算单个相似转换，其中最小的旋转角ti所对应的变换矩阵为最佳相似变换矩阵S;

5) 使用渐入渐出加权融合方法对图像进行融合处理，获得拼接图像。

4 实验与讨论

本文以Matlab R2018a作为实验平台，使用APAP算法[9]数据集中的3组图像，名称和大小分别为：Rail Tracks：600×800×3，Temple：487×730×3，Buiding：662×1 000×3。将本文提出的算法与APAP算法、SPHP算法[10]进行实验并对实验结果进行分析(图1)。

图1 3组原始图像

4.1 时间复杂度分析

表1列出了3种算法在示例图像的消耗时间，首先APAP算法只对一张待拼接图像进行变形，只进行细分网格计算局部单应性矩阵，不对非重区域进行调整，所以相比之下用时最少。SPHP算法不仅需要对待拼接图像进行网格形变，计算局部单应性，还需处理非重叠区域的透视失真问题，所以用时比APAP算法长。本文算法的最佳单应矩阵的计算量不大，只需解决非重叠区域的透视失真问题，同时寻找最佳拼接缝，用时比APAP时间长，但少于SPHP。

表1 3种算法消耗时间 s

4.2 质量效果分析

以Rail tracks的拼接结果为例，图2(a)、图2(b)、图2(c)分别是APAP算法、SPHP算法和本文算法的拼接结果，3种算法对图像完成较为准确的拼接，但在一些细节方面存在差异，如图中红色方框进行标注的3处位置：第一处塔吊在APAP出现明显的错位，而SPHP和本文的算法完成较好的对齐；第二处纹理较复杂的铁路是待拼接图像拼接难度最大的地方，需要算法对重叠区域的纹理进行分析，APAP和SPHP都存在误对齐的现象，而本文的算法基本完成所有轨道的对齐；第三处的树木在APAP算法中因为没有使用最佳相似矩阵进行非重叠区域的单应性过渡，树木出现严重的歪斜变形情况，而SPHP算法和本文算法在非重叠区域的场景进行了很好的保留，没有出现严重的透视变形问题。

图2 图像组Rail tracks 3种方法的拼接结果

图像组Temple与图像组Building利用文中提到的3种方法分别进行拼接实验，拼接结果在图3与图4进行展示，图中利用红色方框进行标注存在明显错位或者重影的地方，本文在标记处的拼接效果均优于其他两种算法，证明本文算法的有效性。

图3 图像组Temple 3种方法的拼接结果

图4 图像组Building 3种方法的拼接结果

为了对3种方法的拼接结果进行客观质量评价，本文引进了NIQE算法[11]对结果图进行评价，NIQE算法是一种无参考通用的失真图像质量评价算法，可针对图像在融合过程中出现的图像失真情况进行有效评价，NIQE得分越小，代表图像质量越好。表2显示了3种算法在图像组中的得分。

表2 3种算法NIQE得分

5 结论

基于最优单应性矩阵的视差图像的拼接算法，结合全局最优单应性矩阵与全局最优相似矩阵对图像进行变形，可以保证图像结构的稳定以及解决非重叠区域的透视失真问题，最优拼接缝寻找算法可以保护重叠区域目标的形状，确保重要目标的保留，同时减少重叠区域的鬼影、误对齐。与APAP、SPHP拼接算法进行对比实验，本算法拼接效果优于二者，但在纹理不明显、视差较大的场景图像下，也出现误配准、错位等现象，需要后续不断优化、改进。