基于流体模型的多智能体分组避障方法

田宝国,吴尚烨

(海军航空大学， 山东 烟台 264001)

当前多智能体控制研究在物流仓储[1]、灾害应急[2]、蜂群作战[3]等方面拥有广泛应用前景。在群体避障方面，Reynolds[4]进行了基础的群体特性研究，Olfati[5]在已有的群体运动控制框架上，设计了基于人工势能函数的群体避障方法。在此基础上相关文献对群体避障方法进行了不同程度的优化，如文献[6]从控制群体密度的角度设计了群体避障方法，能在避障时增大个体间的距离避免个体间或者个体与群体间的碰撞。文献[7]通过赋予智能体记忆功能，使遇到障碍的智能体能通知其他智能体提早改变前进方向有效规避障障物。另外文献[8]通过流函数设计智能体避障的轨道，使群体避障时避免人工势场对智能体造成较多的阻碍。文献[9]中对多智能体遇到不规则障碍的情况进行了路径优化研究。另外文献[10]和文献[11]对多智能体编队避障方法进行了不同程度的优化。类似这样的大多数方法不可避免的需要知道障碍物几何中心以及障碍最大半径长度。在实际情况中，群体常会遇到类似于人群花较多时间离开拥有多条出口通道的体育场或者较大室内的情况。针对于此类情况，上述避障方法对于障碍物几何信息的要求较高，或当群体遇到有多条避障路径可选择时，分布式的决策优化不完善。本文结合文献[12]的研究，将群体视为流体中的组成部分，或是悬浮在流体中的颗粒，通过估算自身在流体中受到的压力从而调整群体中单个智能体的运动方向，进而优化整体避障效率。并类比文献[13]介绍的分层航行群体控制方法，设计多领导者分组领导的群体运动框架增加群体避障时整体的灵活性。

1 问题描述

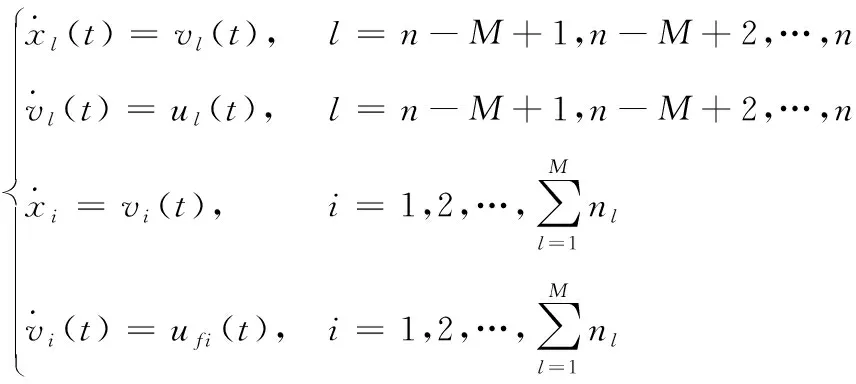
(1)

式中：xl(t)、vl(t)∈R2代表第l个领导者智能体的位置和速度向量；xi(t)、vi(t)∈R2代表跟随者智能体的位置和速度向量；ul(t)、ufi(t)∈R2代表其对应的控制量。

根据olfaite的群体算法框架[5]，在t时刻每个智能体的探测半径为r，则第i个智能体探测到的其他智能体集合为：

Ni(t)={j| ||xi(t)-xj(t)||≤r,j≠i}

(2)

第k个障碍物Ok在第i个智能体探测范围之内时，产生一个该智能体对应的β智能体(障碍物智能体)，其位置为障碍物表面距离智能体最近的点，其坐标可表述为：

(3)

对应第i个智能体探测到的障碍智能体集合为：

(4)

其中，r'为障碍智能体个数；r′为智能体探测障碍智能体的距离。

定义智能体之间的距离范数为[5]：

(5)

其中参数ε>0，且||·||为2-范数。

为简化运动模型，根据文献[14]只考虑智能体之间的排斥函数：

φ(z)=ρh(z/df)[σ1(z-df)-1]

(6)

(7)

由此可定义每对智能体之间的排斥势能为：

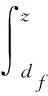
(8)

在现实群体运动中，从观察者角度来看，群体中个体运动速度越大的区域通行效率越高，个体运动速度越慢的区域通行效率越低。考虑到流体运动也有类似的特点，即在同一高度中流速越大的区域压强越低，流速越低的区域压强越大，本文根据流体压强与流速的关系，设计智能体在遇到障碍物时需要受到的额外作用力，从而使群体避障运动具有类似水流遇到障碍物时分流的效果。根据在理想流体条件下的伯努利方程，同一高度上的流速压强公式为[16]：

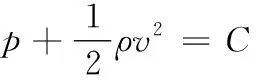
(9)

其中：p为流体压强；ρ为流体密度；v为流体在该点的速度；C为常数。

根据该公式和理想流体条件，设计类似于流体运动的受力模型，将智能群体中每个个体类比为理想流体中根据压力差运动的颗粒，每个颗粒处的速度代表该颗粒区域的流体运动速度，在每个智能体探测出其探测范围内的其他智能体速度后，根据式(9)可计算出每个智能体所在位置的流体压强，由于智能体并不在真实的流体环境中，无法测量真实的受力面积和压力差，只能计算其邻居的压强进而估算自身受到的合力。假设流体密度均匀且ρ为1 kg/m3，不考虑在智能体探测范围内距离远近对压强造成的影响，且对应每个邻居智能体的压强，智能体的受力面积均为1 m3，则第i个智能体单独受到探测范围内某一个智能体的压力大小Fi, j为：

(10)

其中j∈Ni(t)，由此可估算出第i个智能体受到的压强差的合力为：

(11)

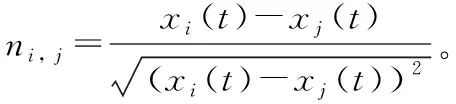
2 控制输入设计

为适应多通道障碍避障，本文采用多领导者分别领导跟随智能体的方法，结合一致性算法保持群体聚集和速度一致性，通过人工势场法避免智能体与智能体之间以及智能体与障碍物之间的碰撞，并通过上述流体模型优化避障路径。由于在该算法中的流体压强差为非线性作用力，为保证最后集群运动的稳定性，设计控制参数Ti，使智能体在速度变慢时根据估算的压力差远离流速慢的区域，并在不需要时取消该作用力，以保持最后群体运动的稳定性，Ti具体描述为：

(12)

其中vp为常数，当Ti=1时，智能体开始计算压力差。当Ti=0时，智能体取消作用在其自身的流体压力。

跟随者智能体控制输入为：

(13)

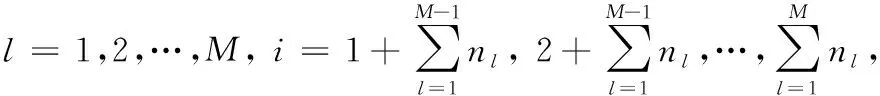
领导者智能体控制输入为：

当l1=n-M+1时，此时为第一个领导者，其控制输入为：

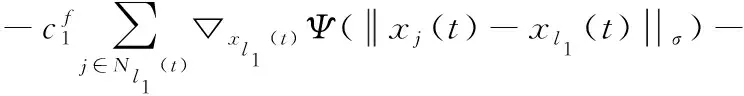
(14)

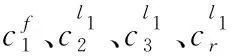
当l=n-M+2,n-M+3,…,n时，从领导者的控制输入为：

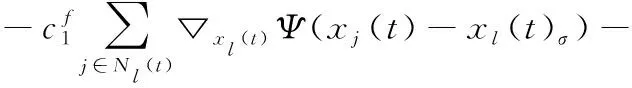
(15)

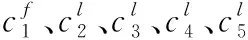
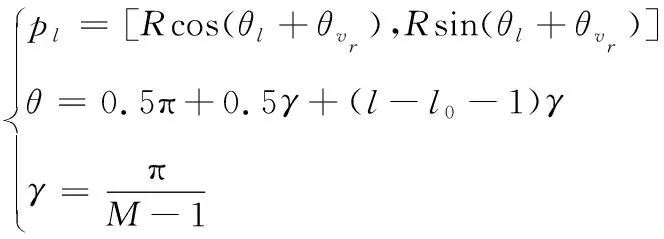
(16)

3 稳定性分析

对于由运动方程(1)和控制输入表达式(13)、表达式(14)、表达式(15)确定的多智能体群集运动系统，当系统智能体总数为n、系统初始时刻能量有限Q(t0)=Q0时，可对t0之后的整体群体系统有以下结论：

1) 当流体作用力不起作用时，跟随者智能体与其对应的领导智能体距离和速度差值存在最大值。

2) 绕过障碍后，从领导者与期望位置差值以及与主领导之间的速度差存在最大值，且从领导者与群体期望速度的差值是有界的。

3) 跟随者速度收敛到其对应的领导者速度，从领导者速度最终收敛到主领导智能体速度，主领导智能体速度收敛到群体期望速度vr。

证明：

在群体避开障碍后或没有遇到障碍时，智能体间流体作用力不起作用，此时，系统总能量方程为：

Q(t)=Qf(t)+Ql(t)+Ql1(t)

(17)

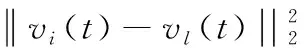
(18)

(vl(t)-vl1(t))Τ(vl(t)-vl1(t))]

(19)

(20)

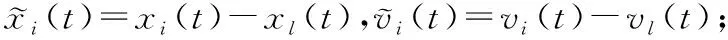
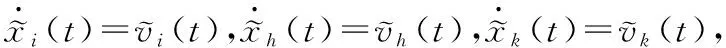
(21)

对函数Q(t)求导，得

(22)

其中

(23)

(24)

ul(t)-ur(t)]

(25)

化简得到：

(26)

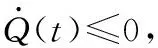
令

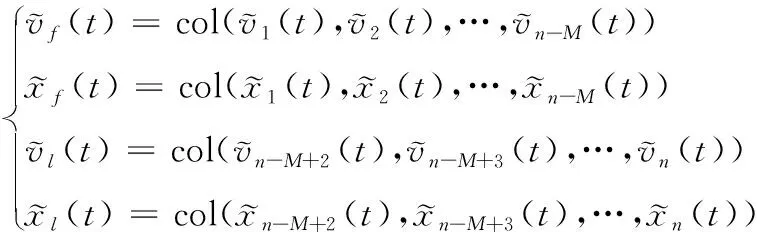
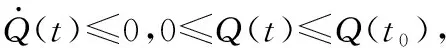
由LaSalle不变集理论[15]知，最大不变集为：

此时vi(t)=vl(t)，vl(t)=vl1(t)，vl1(t)=vr(t)，即主领导智能体速度收敛到群体期望运动速度，从领导智能体速度收敛到主领导智能体速度，跟随智能体速度收敛到其对应领导者速度，所以结论(3)证毕。

4 仿真实验与结果分析

在实际中，障碍往往连在一起且具有多条可选择绕开的路径，同时障碍物位置及其几何信息往往难以第一时间获得，本节实验主要针对此情况下的避障过程进行仿真。

设置6个半径为3.5 m的圆形障碍物，其圆心位置坐标如下：[70,5]，[70,-5]，[70,15]，[70,-15]，[70,-25]，[70,25]。在该障碍分布下，分别就不同群体数量情况下，对使用流体模型的多领导群体和单领导群体，以及不使用流体模型的单领导群体进行仿真实验，并记录6次通过障碍区域的时间，即群体横坐标平均位置在障碍区间x∈[47,93]的时间。具体仿真初始条件如表1所示。

表1 初始条件

其中第3组的群体中从领导者相对主领导者的相对距离都为10 m，跟随主领导者的智能体个数为40，其余每个从领导者智能体各有5个跟随智能体。具体仿真实验结果如表2所示。

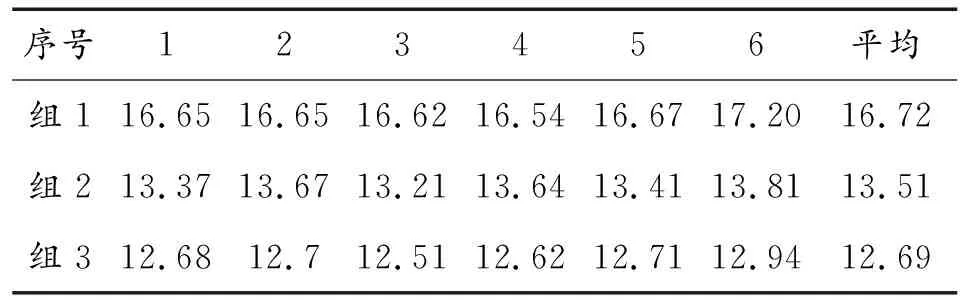
表2 群体避障时间仿真实验结果 s

以上仿真实验中，每组群体均能成功通过障碍区，但避障时间各有不同。根据仿真实验结果，图1为第3组多领导者群体情况下，其中一次仿真实验得到的相关结果。

图1 第3组初始与最终状态仿真实验结果

图1(a)为第3组初始状态，图1(b)为群体通过障碍区后最终状态，由图1可知群体从初始杂乱的随机位置和随机速度最终形成稳定集群，仿真结果与前文理论分析中得到的有关结论相符。

图2为第3组5个领导者智能体的运动轨迹，由图2可知5个领导者智能体在估算的流体压力差作用下分成了3组通过不同的路径。结合图3中群体运动轨迹可发现，在群体通过障碍区域时，整体分布较为均匀，且从两旁绕过了较多的智能体。其避障过程类似于流体遇到障碍时，因为障碍之间空间有限导致流体被障碍分截成多份，最终使分流的群体较为均匀地通过障碍间隙。

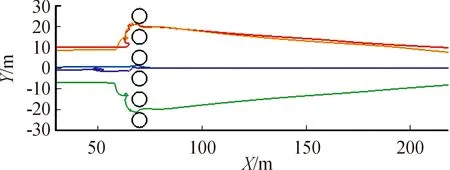
图2 第3组领导者运动轨迹

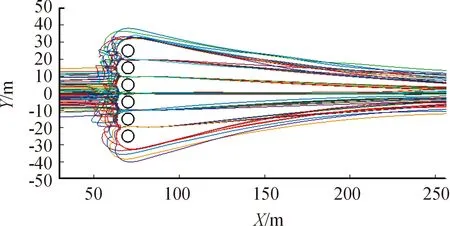
图3 第3组运动轨迹

另外根据领导者的轨迹和群体的轨迹可发现，在群体遇到障碍的一侧，如图中障碍物的左侧，群体轨迹较为紊乱，此现象主要由于位于前部的群体受到障碍物阻碍速度下降，后面的智能体由于排斥力的原因速度随后下降，速度下降到开始估算压力差时，所受合力瞬间增大，造成位于后方的智能体远离前方处于堵塞状态的群体区域，向运动速度相对较高或者没有其他速度较慢智能体的方向。

图4为第3组在Y轴的速度分量变化情况，图5为第3组群体在X轴的速度分量变化情况，由两幅图可知，智能群体最终速度趋向一致，仿真结果符合上节理论分析结果，根据右图群体在X轴运动方向变化情况可知，群体从仿真第800步左右开始到2 500步左右，都有智能体速度处在vx=0 m/s左右振荡，表明仍有部分智能体没绕过障碍，结合本组智能体平均位置在障碍区间的平均时间，可知在大部分群体通过障碍后，小部分智能体仍然处于较为后方的位置。

根据第1组、第2组和第3组仿真实验得到的平均避障时间可知，使用多领导者和流体模型的第3组群体通过障碍区域的平均时间为12.69 s，其比另外1组和2组用时短。同时只有一个领导者且使用流体模型的第2组群体通过障碍区域的平均时间比不用流体模型的第1组实验群体避障时间短。

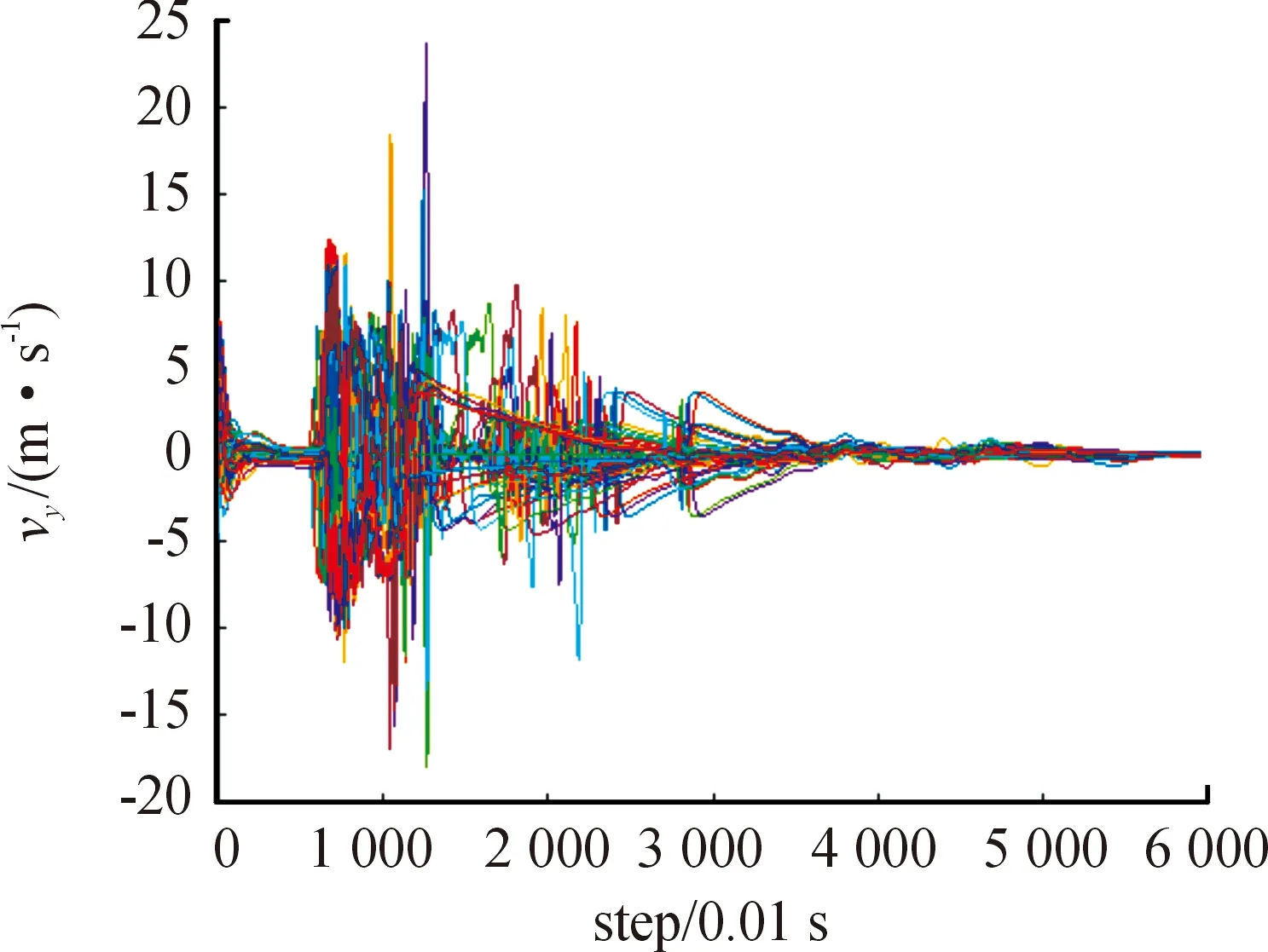
图4 第3组在Y轴速度分量曲线

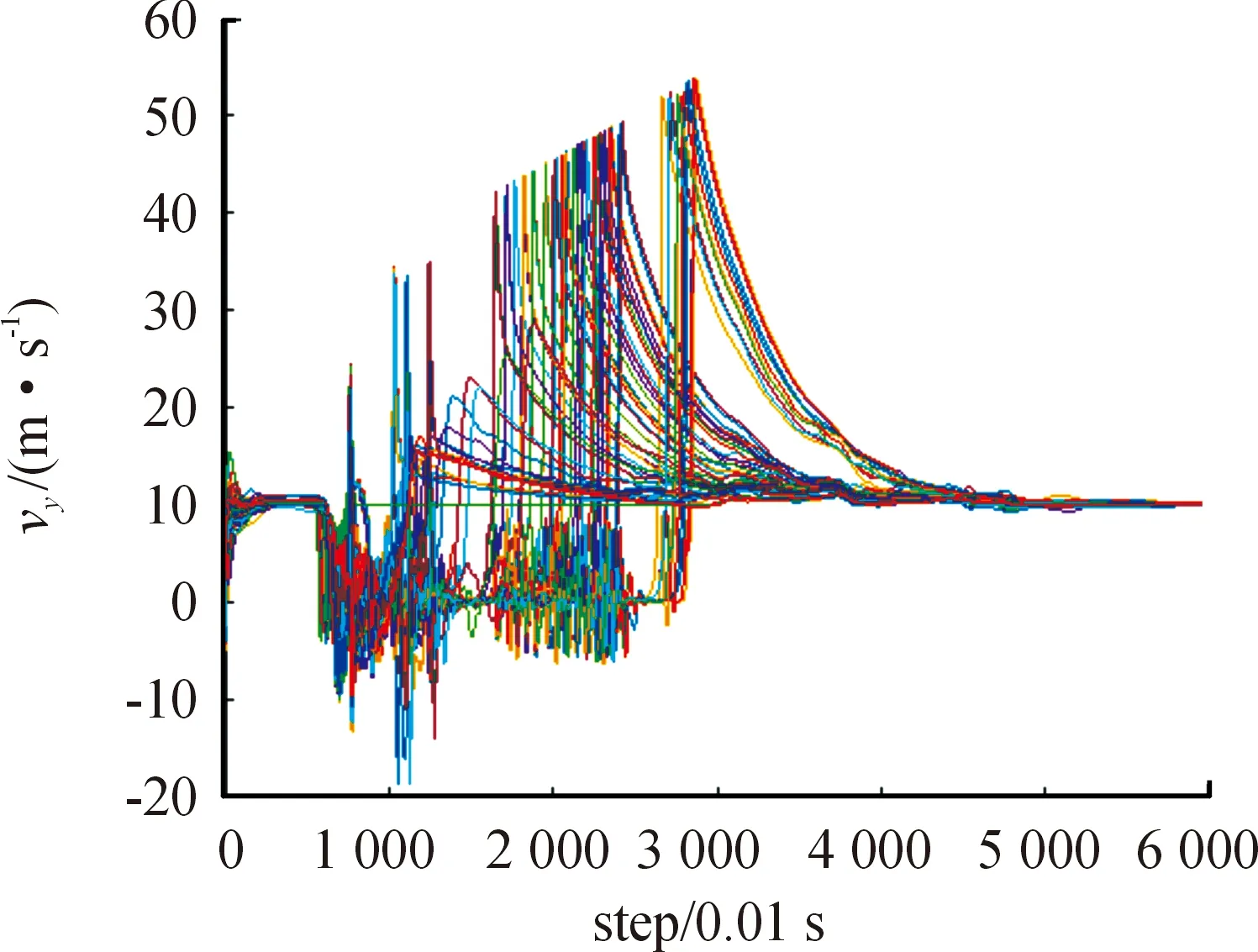
图5 第3组在X轴速度分量曲线

图6为仅用人工势场避障的第1组运动轨迹，图7为单领导者使用流体模型的群体运动轨迹，对比可知，第1组群体通过障碍的路线较为单一，所有智能体仅从三个障碍间隙中通过，而第2组由于使用了流体模型，智能体通过压力差估算，能使智能体向有更高运动速度的区域运动，从宏观上表现为群体被障碍分隔成多条支路。

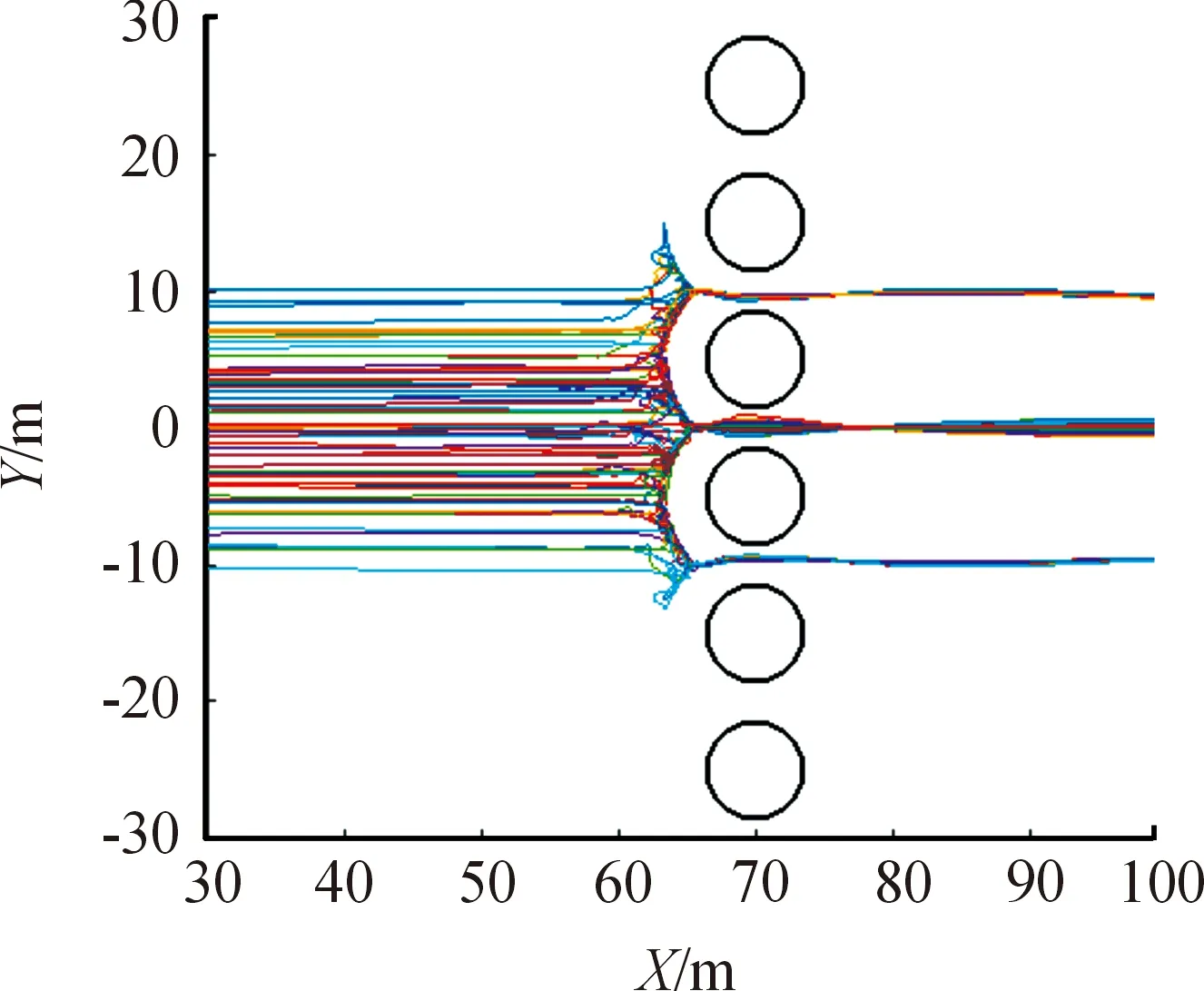
图6 第1组群体动轨迹

图8为第1组群体在X轴方向速度变化图，图9为第2组在X轴方向的速度变化图，对比图5第3组在X轴方向速度运动变化图可知，智能体在X轴方向的速度从vx=0 m/s处振荡，增加到超过vx=10 m/s再逐渐回落到领导者速度vx=0 m/s的变化过程，代表群体从刚通过障碍跟上其跟随的领导者速度，到由于控制输入中的一致性项使智能体速度最终收敛到领导者速度。

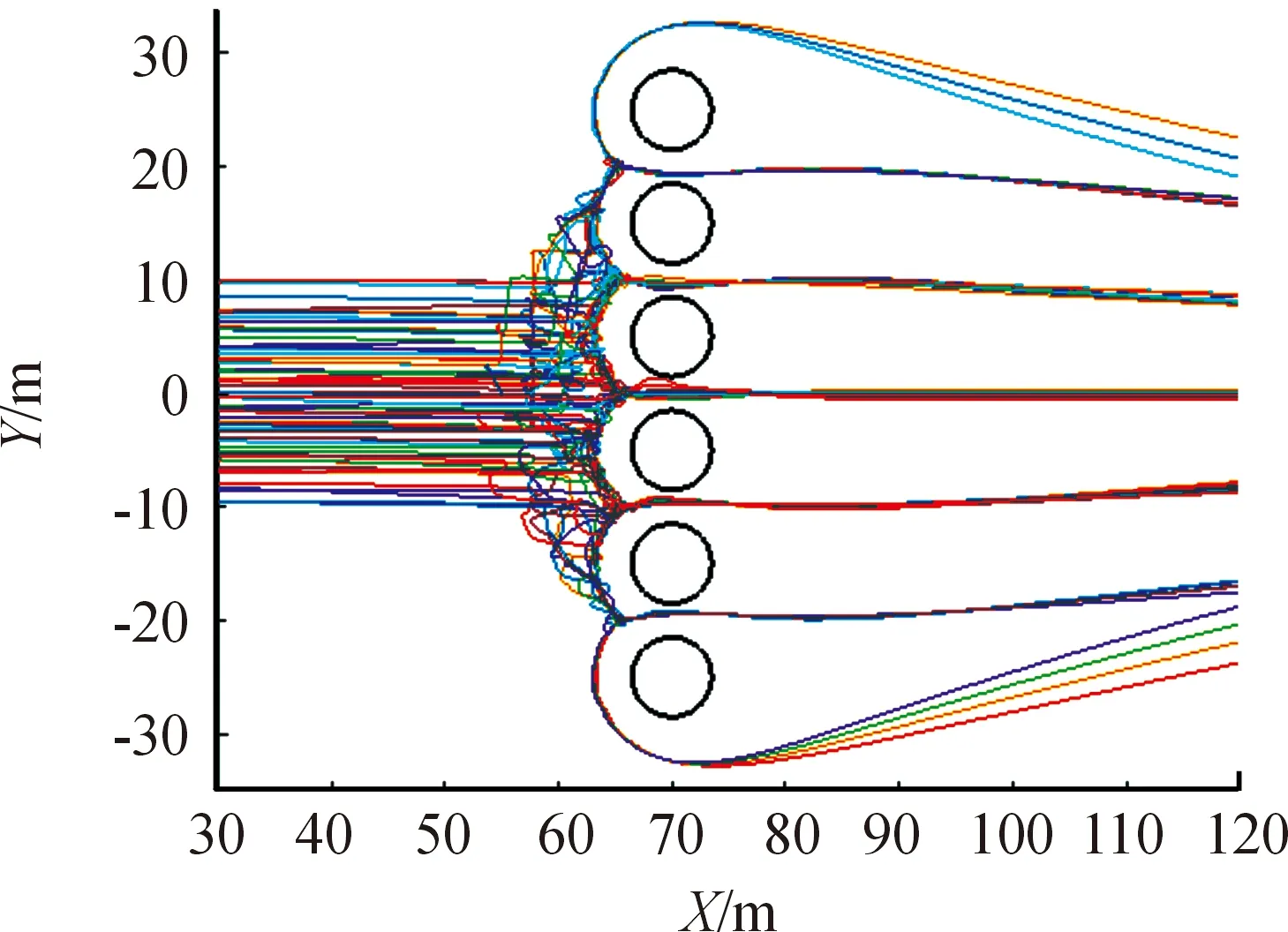
图7 第2组群体运动轨迹

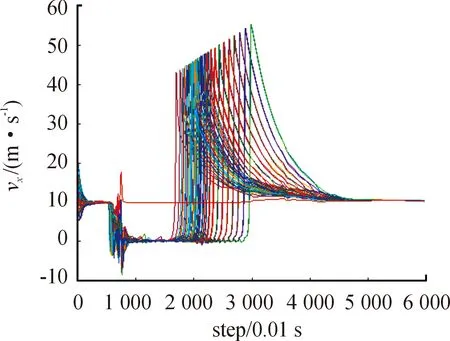
图8 第1组X轴方向速度曲线

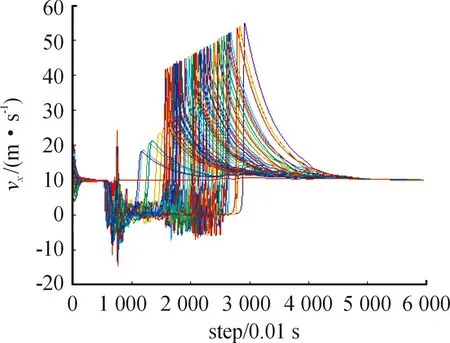
图9 第2组X轴方向速度曲线

根据这3组速度变化情况可知，第1组中大部分智能体从仿真实验的1 600步左右开始通过障碍，而第2组和第3组中从第1 000多步就开始有更多智能体通过障碍，其中第3组在第1 000步以后X轴方向速度变化相对于第2组的速度变化更为剧烈，且根据图7第2组和图3第3组群体运动轨迹可知，第3组的群体除主领导者以外，部分跟随从领导者的智能体从两侧通过的数量更多，从而使群体分流较为均匀，通过障碍的拥挤程度更低，所以第3组的平均避障时间相对第2组的平均避障时间更短。

5 结论

本研究把多智能群体运动类比为理想流体中微粒的运动，并在智能体遇到障碍导致速度减小时估算出其在流体中受到的压力差，在附加压力差下的群体运动整体体现类似于流体的特性。理论分析了群体没有遇到障碍时的稳定性，并在Matlab环境下仿真测试了群体通过具有多通道障碍区的情况，仿真结果表明，在信息有限无法进行路径规划时，对于有多条避障路径的情况下，具有流体模型作用项的避障方法能较为显著的提高避障效率，且分组领导框架使群体更易分开通过不同的避障路径。