提高末制导炮弹在高原地区射击精度研究

刘玉文,段衍安,蒋 明,蔡宏图

(陆军炮兵防空兵学院， 合肥 230031)

世界高海拔地区的国家很少，一般的武器装备设计研制，战技指标的确定主要适应于平原或低海拔地区。随着海拔高度的增加，特别4 000 m以上，空气密度变得稀薄，弹道特性发生显著变化。对于制导武器，同等条件下打舵产生的控制力下降，制导范围发生变化，制导效率下降，甚至脱靶不能命中目标。本文通过理论分析，以榴弹弹道方程和导弹制导方程为基础，通过模拟计算，从技术改进和射击指挥2个方面对激光末制导炮弹在高原地区射击精度进行探讨。

1 射击精度下降原因

1.1 制导范围及其随海拔高变化规律

以海拔0 m时某激光末制导炮弹制导范围为基础，对应完全相同的射击条件，根据弹道方程和制导方程[1-2]，在不同海拔条件下，对其制导范围进行仿真计算。在海拔高0～5 000 m内，计算结果如图1所示。

由图1可知，随着海拔高的增加，制导范围变小，海拔高5 000 m对应的制导范围比0 m海拔对应的制导范围减小达到65%。

仿真可给出360°制导范围内的边界点坐标数值。表1给出了炮阵地高程0 m和5 000 m对应的制导范围(左右边界点)数据。在阵地高程0 m制导范围对应的射程差为1 832 m，阵地高程5 000 m时，射程差为1 154 m，减小37%。同样，最大横向范围，阵地高程5 000 m时，减小36%。

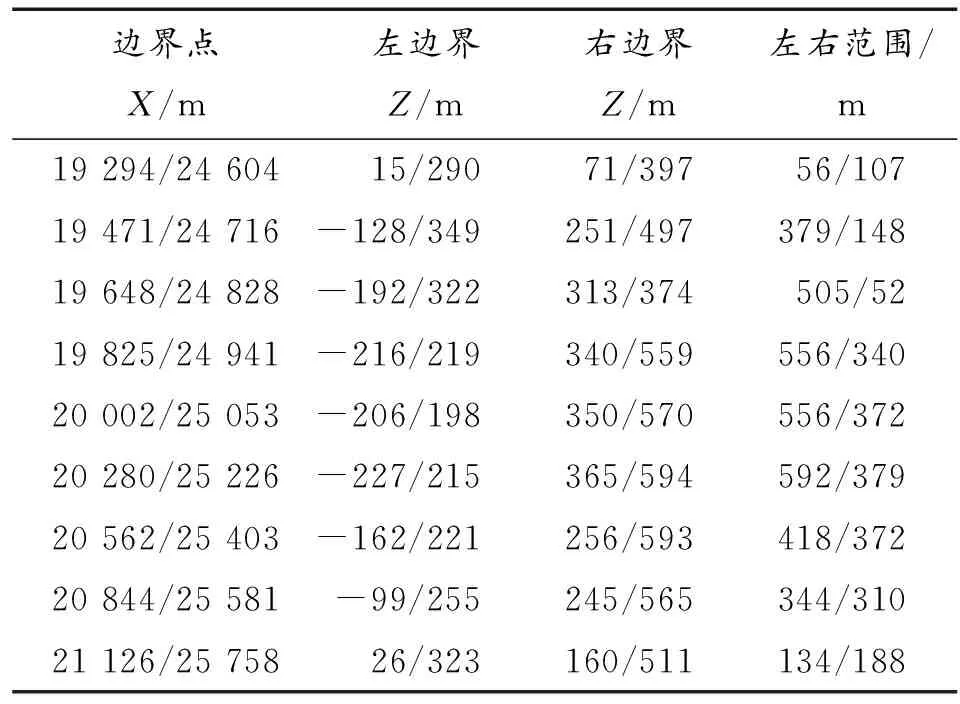
表1 阵地高程0 m/5 000 m制导范围边界点数据表

制导范围随海拔高增加而变小的主要原因是随着海拔的增加，空气密度减小，导致的舵翼实际控制效率下降，尽管高原条件下舵翼偏转角度与平原相比没有变化，但提供的控制力却比平原条件下小，因而导致制导范围变小。

1.2 精度下降与掉弹情况

制导范围的减小，表明在这个范围外的目标，命不中(原来在平原地区能命中的)，命中概率下降。

除了上述制导范围下降这个主因外，射击精度下降原因还有：

1) 高原气象规律与平原地区不同以及弹道特性的变化[3](非制导段)，导致该弹可能：落入激光感知的“栅栏”内(若在栅栏边沿情况更差点)，这种情况，能寻的制导，但因制导能力下降，不能在有限的制导时间内命中制导范围外的目标；不能进入栅栏内，不能寻的制导。

2) 空气稀薄，原定的下滑位置、时间和弹道倾角等参数难于满足重力补偿要求[4]，射距离大大缩短，再加上制导效率下降，弹丸落点比预定点近很多。

2 提高射击精度的方法

根据上述模拟计算和理论分析，可知随着海拔高增加，高原气象误差、弹道特性变化以及制导炮弹制导范围减小的综合影响，将导致命中概率下降。从武器系统本身考虑，解决这一问题的技术途径是适度增大舵偏角或条件允许延长激光照射时间，其次，是从射击指挥角度，尽力提高射击诸元精度和进行符合修正(当然，这是被动的，不是解决问题的根本方法)。

2.1 增大舵偏角

由于激光末制导炮弹采用的是乒乓舵，只在水平舵位于水平位置或垂直位置时，舵机才工作[5]。舵机工作时，提供固定的舵偏角，提供气动控制力。弹体转过水平位置或垂直位置后，舵片偏转角回到0°。飞行过程中的打舵时机主要由弹载的自动驾驶仪通过控制回路运算得到。对不同海拔高增大舵偏角时的弹道进行了仿真计算。

仍以“1”中计算条件，选取相同的射击诸元，海拔高程选取4 000 m，舵偏角分别取θ1、θ2(θ2=θ1+1°)和θ3(θ3=θ1+2°)，进行制导范围的计算。制导范围随舵偏角的变化如图2所示。

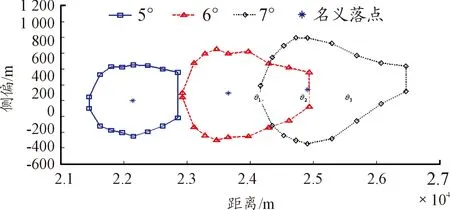
图2 海拔高4 000 m时不同舵偏角制导范围示意图

从图2中可以看出：随着舵偏角的增加，落点射程增加，左右边界数值增加，制导的最远距离和最近距离的数值都增加，制导范围总体增大。舵偏角θ2时的制导范围面积比θ1时增大约45%，舵偏角θ3时制导范围面积比θ1时增加约96%。具体对应的制导范围边界点数据如表2所示。

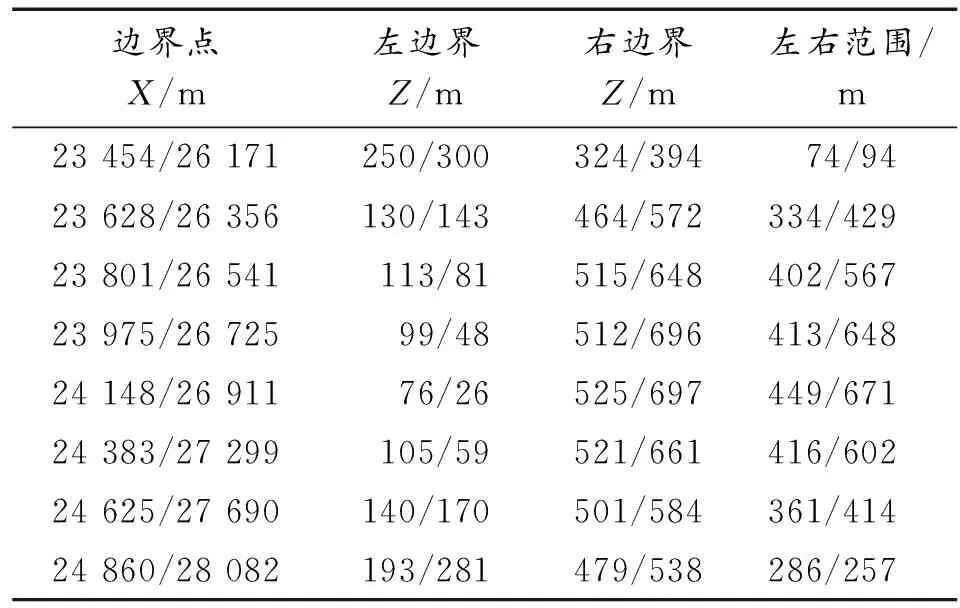
表2 舵偏角θ1/θ3制导范围边界点数据表

舵偏角增大，使得制导范围增加，这对于提高其射击精度是有益的。但从弹道特性方面看，舵偏角增大，将使得弹体的气动特性改变更大，弹丸飞行过程中的角运动会加剧，动力平衡角增大，容易发生飞行失稳，因此，舵偏角只能适度增大。

2.2 延长激光照射时间

末制导炮弹在末段接受目标反射来的激光信号之后，通过弹载自动驾驶仪生成控制信号，控制舵机偏转。现行的激光目标指示器，由于其最大工作时间一定，若能延长激光照射时间，使得激光末制导炮弹尽早进入末段制导段，则有利于提高其在高海拔条件下的制导精度(范围)。

仍以“1”中计算条件，选取相同的射击诸元，阵地高程选取4 000 m，舵偏角取θ1，激光照射时间分别取t1、t2(t2=t1+5 s)和t3(t3=θ1+10 s)进行制导范围计算。制导范围随照射时间的变化如图3所示。

图3 海拔高4 000 m时不同激光照射时间制导范围示意图

从图3可以看出：延长激光照射时间，在相同的射击诸元情况下，制导范围增加。照射时间为t2时，制导范围比照射时间为时的制导范围增加约2.5倍，但激光照射时间延长至t3后，制导范围和照射时间为t2时的制导范围相比增加不太明显。照射时间为t1时的制导范围边界点数据表与表2中θ1时相同，照射时间为t2和t3对应的制导范围边界点数据见表3所示。

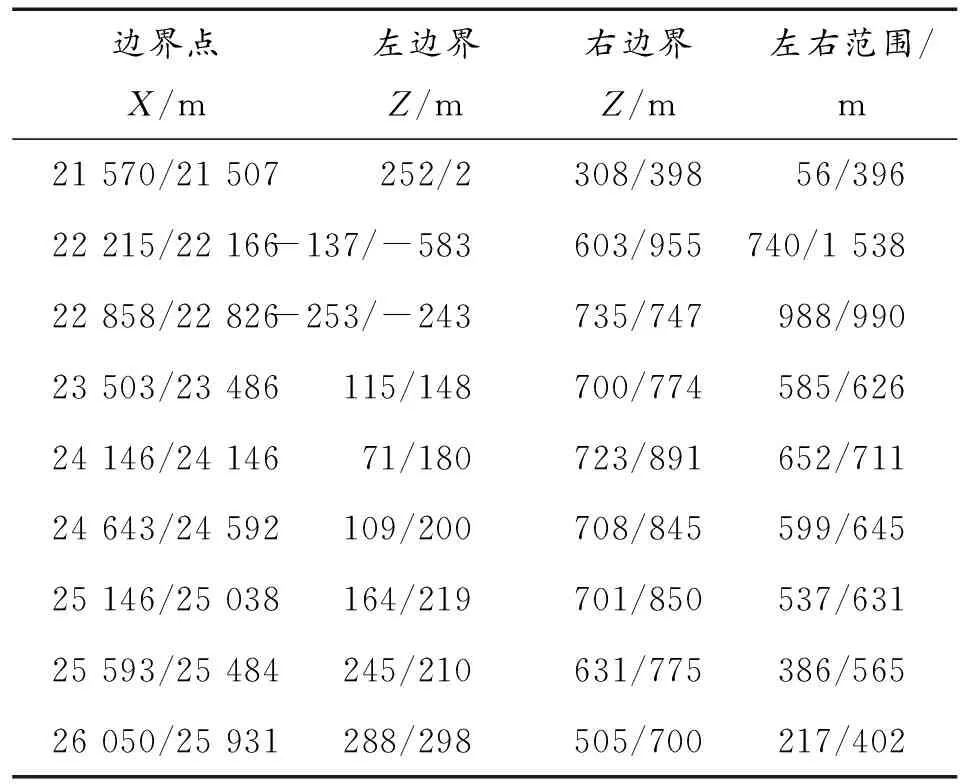
表3 照射时间t2/t3制导范围边界点数据表

仿真计算结果表明，海拔4 000 m时，激光照射时间t2，可以显著增加制导范围，因此，在高原条件下，延长激光照射时间可以有效增大制导范围。

2.3 基于射击的提高精度方法

通过上述分析与计算可知高原弹道特性的变化以及制导能力的下降是导致命中精度下降的主要的根源，必须从武器系统本身进行技术改进。在问题没有得到解决之前，我们从射击指挥角度，分析研究提高射击精度有关方法措施。

2.3.1提高气象诸元精度

高原气象变化很快，地形起伏较大，随机风明显，气象稳定性差，给气象探测带来困难[6-7]。当前，气象诸元的误差相比于其他误差是比较大的，气象诸元精度直接影响自由段和制导段弹道，可能导致不能进入激光制导“栅栏”内。因此，加密气象探测和提高气象诸元精度十分重要。

2.3.2提高射击诸元精度

激光末制导炮弹利用精密法决定射击开始诸元要进行二次迭代求开始距离，可见对射击开始诸元精度要求之高(比普通榴弹还高)。从弹道上看，全弹道可分为自由飞行段和制导段。这里我们通过命中概率模型，来揭示影响射击精度因素和提高精度方法。

1) 自由飞行段命中概率数学模型。设末制导炮弹有效制导幅员的正面和纵深分别为2b和2a，在诸元误差为(xc,zc)的条件下，发射1发激光末制导炮弹，命中有效制导幅员的条件概率为：

(1)

利用拉普拉斯函数，可得

(2)

再考虑诸元误差的整体性，发射1发激光末制导炮弹落达有效制导幅员的概率P1为：

(3)

2) 制导段命中概率数学模型。设目标毁伤幅员的正面和纵深分别为2lx和2lz，瞄准位置位于目标中心，以目标中心为坐标原点，在制导段命中目标的概率为

(4)

制导段的命中概率，实质上是个条件命中概率，是激光末制导炮弹在自由飞行段命中有效制导幅员的条件下，在制导段接收激光信号，命中目标的概率。所以激光末制导炮弹命中概率为

P=P1×P2

(5)

即：

(6)

由式(6)可以看出，影响命中概率的因素有很多，其中影响自由飞行段命中概率的因素有诸元误差(Ed,Ef)、散布误差(Bd,Bf)以及有效制导幅员的大小。影响制导段命中概率的因素有导引误差(Em)和照射误差(L)。这些因素中，散布误差(Bd,Bf)、导引误差(Em)取决于武器系统的性能，而诸元误差(Ed,Ef)、照射误差(L)的大小，直接取决于射击诸元精度及正确的照射训练方法。

图4是在某一射距离、有效制导幅员、散布误差条件下，改变诸元精度Ed，自由飞行段命中概率曲线。

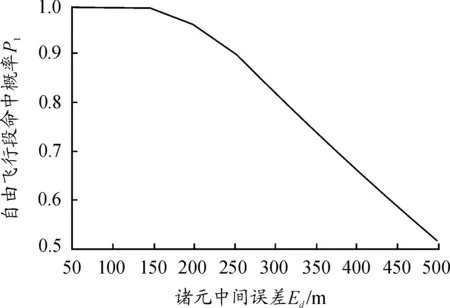
图4 自由飞行段命中概率曲线

可以看出，自由飞行段激光末制导炮弹的命中概率随诸元中间误差的增大而减小。诸元精度不高，直接影响P1大小，当诸元精度下降到一定值时，如P1下降到0.8以下，即使P2达到1，命中概率也不大于0.8，这与该类制导炮弹要求的命中概率不符。所以，在末制导炮弹作战使用时，要保证对目标的精确打击，高度重视诸元误差。

2.3.3适当加入经验修正和系数符合

事实证明，从远向近修正，因重力作用，打舵容易点。操作中，宁愿射角加大一定密位，便于下打舵。在大的修正距离下，这样的考虑也是没办法的办法(在弹丸没有进行技术改进之前)。同时，根据不同海拔弹道特性和制导范围的计算概略值，做相应诸元调整符合，相当于考虑了部分海拔产生的影响，当然这要有一定数量的实弹射击和实际操作经验。

2.3.4指火控系统射击模型修改

高原弹道特性的变化，导致气动参数发生变化。因此，在指火控系统中，弹道和射击诸元模型要作相应的调整,以适应高原[8]。若用射表，要采用“真正”的高原射表，若用解算弹道决定射击诸元，要使用高原气动参数[9]，以提高射击精度。

3 结论

随着海拔高度的增加，弹道特性的变化越来越显著，制导弹丸更是如此。这种弹道特性的变化必将影响到制导弹丸射击精度。通过模拟计算表明对于激光末制导炮弹，增加舵偏角和延长激光照射时间是增大制导范围，提高命中精度的技术和根本途径。至于舵偏角具体增大多少，照射时间延长多少则需要根据战技指标的新要求进行针对性计算。