解析几何中以“数列”为命题背景的问题求解策略

◇ 四川 李 波

解析几何中的数列问题以直线与圆锥曲线为载体,与基本量a,b,c、直线(斜率、弦长)、向量等知识相结合,考查等差、等比数列基本量的求解及证明,涉及数形结合、等价转化、分类讨论、设而不求等思想方法.该类题型在2013年、2016年、2018年高考真题中均出现过,考生常出现运算中代数变形方向性不明、运算盲目等问题.为突破这一瓶颈,本文总结出问题突破点,归纳解题技巧与策略,以期帮助读者在学习中做到选择捷径、简化计算、避繁就简.

1 建方程组,消元求解

例1定义:离心率的椭圆为 “黄金椭圆”,已知的一个焦点为F(c,0)(c＞0),则E为“黄金椭圆”是a,b,c成等比数列的( ).

A.既不充分也不必要条件

B.充分且必要条件

C.充分不必要条件

D.必要不充分条件

解析

(充分性)由a,b,c成等比数列可知,显然a2－ac－c2＝0,等式两边同时除以a2,得e2＋e－1＝0,解得,所以E为“黄金椭圆”.

(必要性)由E为“黄金椭圆”知,显然离心率e满足e2＋e－1＝0,又,所以a2－acc2＝0,由a2－b2＝c2,知b2＝ac,所以a,b,c成等比数列.故选B.

练习已知椭圆的一个焦点为F(c,0)(c＞0),若a,b,c成等差数列,则椭圆的离心率为________.

点评

解题时要充分挖掘基本量a,b,c的隐藏信息,并结合题中已知信息运用方程组思想消元,从而找到问题的突破口.

2 回归定义,以逸待劳

例2已知抛物线C:x2＝4y的焦点为F,抛物线上A,B两点处的切线交于点P.证明:|AF|,|PF|,|BF|成等比数列.

解析

由抛物线定义可知,|AF|＝y1＋1,|BF|＝y2＋1,所以|AF|·|BF|＝y1y2＋y1＋y2＋1,又|PF|2＝y1＋y2＋y1y2＋1,显然|AF|·|BF|＝|PF|2,即|AF|,|PF|,|BF|成等比数列.

例3(2013年全国卷)已知双曲线(a＞0,b＞0)的左、右焦点分别为F1,F2,离心率为3,直线y＝2与C的两个交点间的距离为6.

(1)求a,b;

(2)设过F2的直线l与C的左、右两支分别交于A,B两点,且|AF1|＝|BF1|,证明:|AF2|,|AB|,|BF2|成等比数列.

解析

(1)a＝1,b＝22(求解过程略).

(2)设A(x1,y1),B(x2,y2),由题可知,直线AB的斜率存在,设直线AB的方程为y＝k(x－3),则y1＝k(x1－3),y2＝k(x2－3),由对称性,不妨假设k＞0,联立消y得

由|AF1|＝|BF1|知,kAB·kPF1＝－1,即,解得,此时

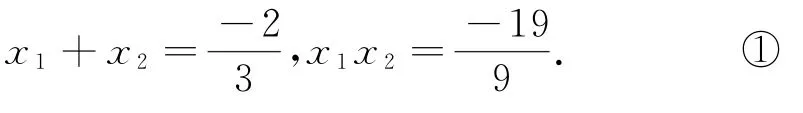
由点A在双曲线上,知,所以

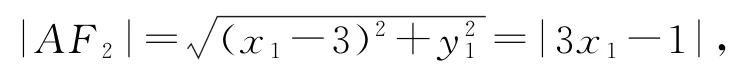
同理|BF2|＝|3x2－1|,所以

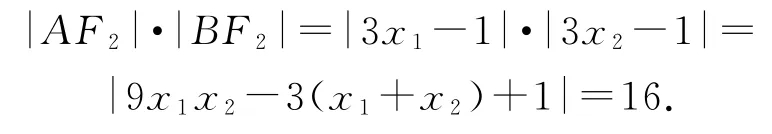
由双曲线的定义知

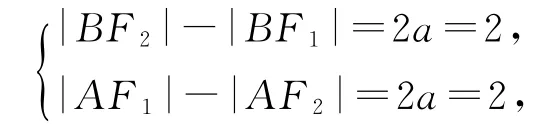
解得|BF2|－|AF2|＝|AB|＝4,显然|AF2|·|BF2|＝|AB|2,即|AF2|,|AB|,|BF2|成等比数列.

另解,将式①代入上式得,|AB|＝4,显然有|AF2|·|BF2|＝|AB|2,即|AF2|,|AB|,|BF2|成等比数列.

点评

利用数形结合思想和圆锥曲线定义巧妙求出线段长度,运用数列知识验算,达到事半功倍的效果,也体现了“多一点想,少一点算”的命题思想.

练习设F1,F2分别是椭圆(a＞b＞0)的左、右焦点,过F1作斜率为1的直线l与E相交于A,B两点,且|AF2|,|AB|,|BF2|成等差数列.

(1)求椭圆E的离心率;

(2)设点P(0,－1)满足|PA|＝|PB|,求E的方程.

3 设而不求,巧用定理

例4(2013年江西卷理20)如图1所示,椭圆过点,离心率直线l的方程为x＝4.

(1)求椭圆C的方程;

(2)AB是经过右焦点F的任一弦(不经过点P),设直线AB与直线l相交于点M,记PA,PB,PM的斜率分别为k1,k2,k3.问:是否存在常数λ,使得k1＋k2＝λ2k3? 若存在,求λ的值;若不存在,说明理由.

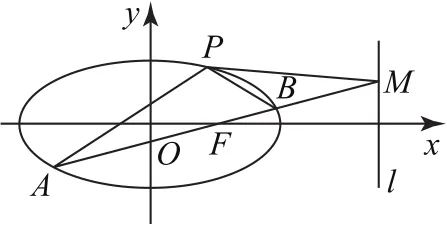
图1

解析

(2)设A(x1,y1),B(x2,y2),由题知,直线AB的斜率存在,设直线AB的方程为y＝k(x－1),则

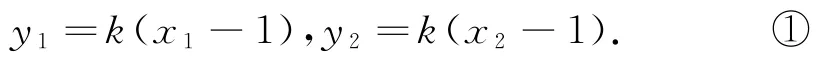
由题意可知,PA,PB的斜率分别为

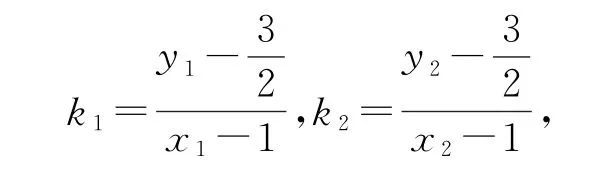
将式①代入上式得

将式②代入上式得k1＋k2＝2k－1.易知M(4,3k),所以,显然k1＋k2＝2k3.

综上,存在常数λ＝2符合题意.

点评

本题主要考查代数运算、等差数列、直线与圆锥曲线的位置关系等知识,突出根与系数的关系、设而不求思想等,旨在考查学生的运算求解能力,转化与化归、数形结合思想,考查的核心素养是逻辑推理.

练习(2018年全国卷Ⅲ理20)已知斜率为k的直线l与椭圆交于A,B两点,线段AB的中点为M(1,m)(m＞0).

(2)设F为C的右焦点,P为C上一点,且成等差数列,并求出该数列的公差.

4 极端策略,围魏救赵

例5已知F是椭圆的右焦点,椭圆上至少有21个不同的点Pi(i∈N∗),|FP1|,|FP2|,|FP3|,…组成公差为d(d＞0)的等差数列,则( ).

A.该椭圆的焦距为6 B.|FP1|的最小值为2

C.d的值可以为

解析

易知a＝5,b＝4,c＝3,由椭圆的性质知ac≤|PF|≤a＋c,即|PF|∈[2,8],不妨设a1＝2,则a21＝a1＋20d≤8,解得.故选项ABC正确,选项D错误.

例6已知点P为双曲线0)上任意一点,过点P作双曲线的渐近线的平行线,分别与两渐近线交于M,N两点,若b是|PM|,|PN|的等比中项,则该双曲线的离心率为________.

特殊解法设点P的坐标为(a,0),联立得是|PM|,|PN|的等比中项,所以|PM|·|PN|＝b2,即a2＝3b2,则该双曲线的离心率.

点评

从＂特殊到一般＂是数学学习过程中常用的思想方法,也符合当前中学生的认知规律,从特殊情况入手,对求解选择题和填空题而言,能为考生节约大量的时间;对求解解答题而言,能为考生寻找问题的突破口并指明方向.这种方法对探究新知起指导作用,既服务教学,又服务实践.

练习已知双曲线的离心率为2,过右焦点且垂直于x轴的直线与双曲线交于A,B两点.设A,B到双曲线的同一条渐近线的距离分别为d1,d2,且d1,3,d2成等差数列,则双曲线的方程为( ).

5 巧设参数,变换主元

例7过抛物线y2＝2px(p＞0)的焦点F作斜率为k的直线,与抛物线相交于A,B两点,设直线OA,OB(O为坐标系原点)的斜率分别为k1,k2,则下列等式正确的是( ).

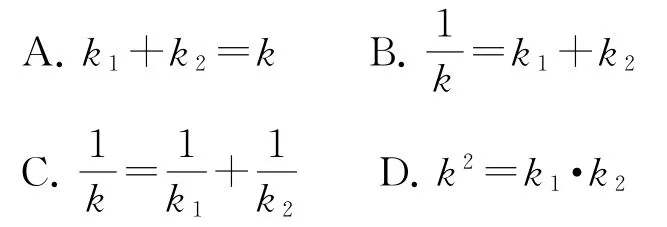
解析

点评

本解法属于比较常规的解法,巧妙地运用抛物线的参数方程进行设点,避免了联立方程组,计算相对简单,但是解法中含有两个参数y1,y2,因此要注意变形过程的等价性.

例8在平面直角坐标系xOy中,曲线C的参数方程为且倾斜角为α的直线l交曲线C于A,B两点.

(1)求曲线C的普通方程和直线l的参数方程;

(2)若|PA|,|AB|,|PB|成等差数列,求tanα.

解析

(1)曲线C的普通方程为,直线l的参数方程为(t为参数).

(2)设A,B两点对应的参数分别为t1,t2,将直线的参数方程代入椭圆方程得

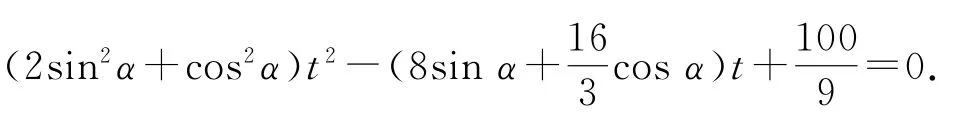
由根与系数的关系得

将上式代入

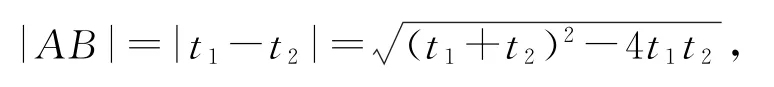
又|PA|,|AB|,|PB|成等差数列,所以

故有23sin2α－36sinαcosα＋13cos2α＝0,等式两边同时除以cos2α,得

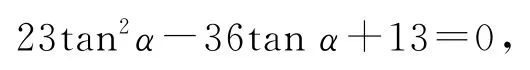
点评

将坐标中两个变量转化为一个变量,方便在化简、求最值时使用均值不等式或构造函数判断单调性或比较大小.

练习已知圆K过定点A(a,0)(a＞0),圆心K在抛物线C:y2＝2ax上运动,MN为圆K在y轴上截得的弦.

(1)试问MN的长是否随圆心K的运动而变化;

(2)当|OA|是|OM|与|ON|的等差中项时,抛物线C的准线与圆K有怎样的位置关系?

6 巧用平几,妙手回春

例9如图2所示,已知椭圆,与x轴不重合的直线l经过左焦点F1,且与椭圆G相交于A,B两点,弦AB的中点为M,直线OM与椭圆G相交于C,D两点.

(1)若直线l的斜率为1,求直线OM的斜率;

(2)是否存在直线l,使|AM|2＝|CM|·|DM|成立?若存在,求出l的方程;若不存在,请说明理由.

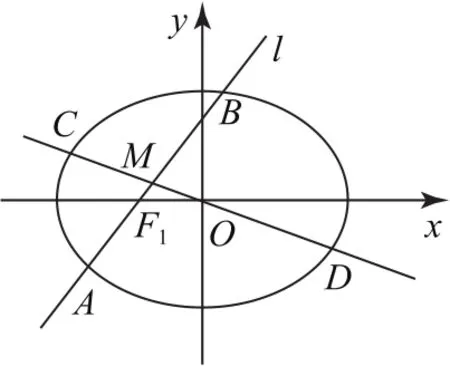
图2

解析

(1)直线OM的斜率为(求解过程略).

(2)假设存在直线l,使得|AM|2＝|CM|·|DM|成立.当直线l斜率不存在时,易知此时M与F1重合,则

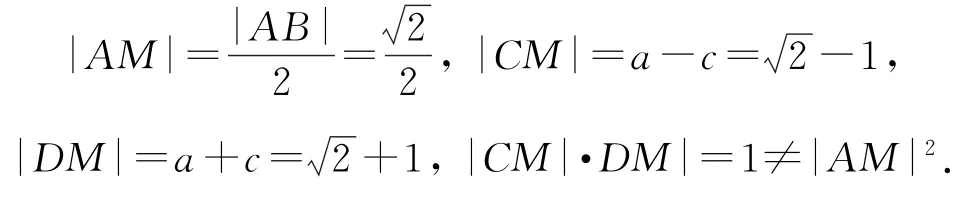
当直线l斜率存在时,设A(x1,y1),B(x2,y2),直线AB的方程为y＝k(x＋1),不妨假设k＞0,则得(1＋2k2)x2＋4k2x＋2k2－2＝0,由根与系数的关系知

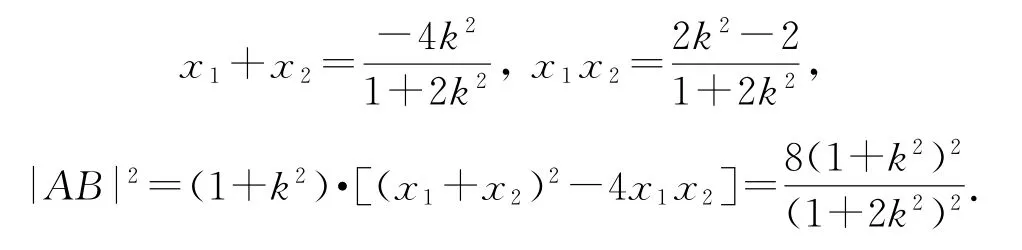
易知线段AB中点由题意,直线l不与x轴重合,所以直线OM斜率联立解得点C坐标为.

因为|AM|2＝|CM|·|DM|＝(|OC|－|OM|)·(|OD|＋|OM|),且|OC|＝|OD|,所以|AM|2＝,即

点评

本题第(2)问的核心在于转化|AM|2＝|CM|·|DM|中弦长的关系.由|CM|＝|OC|－|OM|,|DM|＝|OD|＋|OM|,又|OC|＝|OD|,可得|AM|2＝|OC|2－|OM|2.又|AM|＝因此|AB|2＝4|OC|2－4|OM|2,转化为弦长|AB|,|OC|和|OM|三者之间的数量关系,从而使问题获解.

例10设一簇双曲线N∗,n≤2019),直线x＝2与En在第一象限的交点为An,An在En的两条渐近线上的投影分别为Bn,Cn,记△AnBnCn的面积为an,求a1＋a2＋…＋a2019的值.

解析

将x＝2代入双曲线的方程,可得y＝又因为双曲线的渐近线方程为y＝±x,所以点An到渐近线y＝x的距离,点An到渐近线y＝－x的距离,易知四边形OAnBnCn为矩形,所以,所以

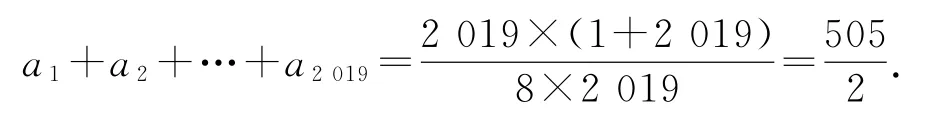
练习(2016年四川卷)已知数列{an}的首项为1,Sn为数列{an}的前n项和,Sn＋1＝qSn＋1,其中q＞0,n∈N∗.(1)若2a2,a3,a2＋2成等差数列,求an的通项公式;(2)设双曲线的离心率为en,且,证明.

定值问题、最值问题、参数问题、应用题和探索性问题等与圆锥曲线知识纵向联系.圆锥曲线知识和三角、数列等代数知识相结合,属于横向联系.解答这部分试题,需要较强的代数运算能力和图形认识能力,要能准确地进行数与形的语言转换和运算,并在运算过程中注意思维的严密性和结果的完整性.