双曲线的重要性质及应用
2020-12-15陕西魏文宏
◇ 陕西 魏文宏

图1
1 结合对称性的应用
例1已知F1,F2是双曲线的左、右两焦点,若双曲线左支上存在一点P与点F2关于直线对称,则a的值为________.
解析
如图2所示,P与F2关于直线对称,连接PF2与直线交于点M,由性质有|OM|=a,|F2M|=b=1,|PF2|=2b=2,由OM为△PF1F2的中位线知|PF1|=2a,结合双曲线的定义有2-2a=2a,解得.

图2
例2已知F1,F2是双曲线b>0)的左、右两焦点,若双曲线左支上存在一点P与F2关于直线对称,则此双曲线的离心率为________.
解析
设P与F2关于直线对称,连接PF2与直线交于点M,根据双曲线的性质有|OM|=a,|F2M|=b,|PF2|=2b,由OM为△PF1F2的中位线可知|PF1|=2a,结合双曲线的定义有2b-2a=2a,解得则离心率e=.
例3过双曲线的右焦点F作一条渐近线的垂线,垂足为A,与另一条渐近线交于点B,点Q是圆x2+y2=a2上的一个动点.若的最大值为6,则双曲线的方程为________.
解析

图3
例4已知双曲线的左焦点为F,A是双曲线C的左顶点,双曲线的一条渐近线与直线且FP⊥AM,则双曲线C的离心率为( ).

解析
如图4所示,由双曲线的性质可知,FP⊥OP,|FP|=b,|OP|=a,|OF|=c.又因为且FP⊥AM,所以AM垂直平分FP,AM为△OPF的中位线,所以
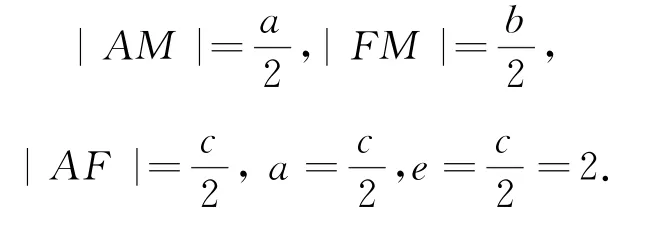

图4
例5已知双曲线的左、右焦点分别为F1,F2,过点F1作圆x2+y2=a2的切线交双曲线右支与点M,若则双曲线的离心率为( ).
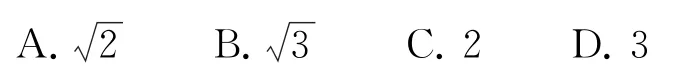
解析
如图5所示,由双曲线的性质知,F1P⊥OP.|F1P|=b,|OP|=a,|OF1|=c.作F2Q⊥F1M于Q,则
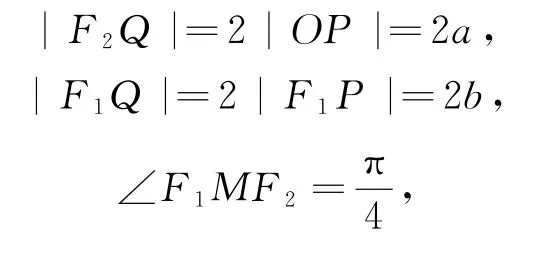

图5
|QM|=|F2Q|=2a,,由双曲线的定义知,|MF1|-|MF2|=2a,即2b+,故选B.
2 在高考中的应用
例6(2019年全国卷Ⅰ理16)已知双曲线C:的左、右焦点分别为F1,F2,过F1的直线与C的_两条渐近线分别交于A,B两点.若则C的离心率为_____.
解析
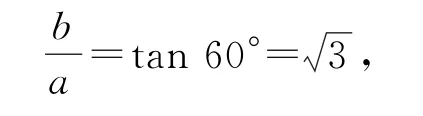
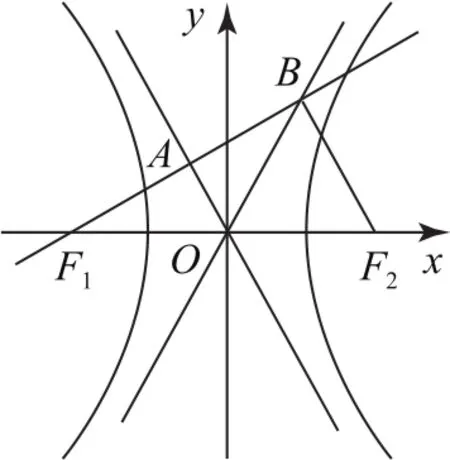
图6

例7(2018年天津卷理7)已知双曲线1(a>0,b>0)的离心率为2,过右焦点且垂直于x轴的直线与双曲线交于A,B两点.设A,B到双曲线同一条渐近线的距离分别为d1和d2,且d1+d2=6,则双曲线的方程为( ).

解析
如图7所示,由d1+d2=6,得双曲线的右焦点到渐近线的距离为3,所以b=3.因为双曲线(a>0,b>0)的离心率为2,所以所以,解得a2=3,所以双曲线的方程为故选C.

图7
例8(2018年全国卷Ⅲ理11)设F1,F2是双曲线的左、右焦点,O是坐标原点.过F2作C的一条渐近线的垂线,垂足为P.若则C的离心率为( ).


图8
解析
如图8所示,由双曲线的性质知|OP|=a,|F2P|=b,在Rt△F2PO中,|F2O|=c,|OP|=a,所以c,所以在△F1PO与Rt△F2PO中,根据余弦定理得
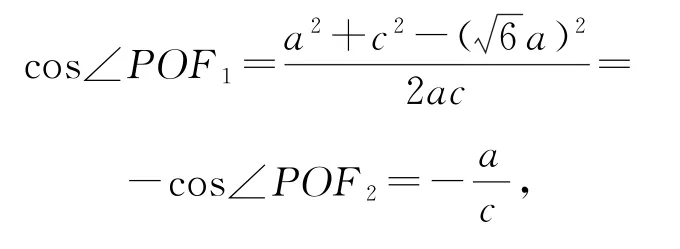
即3a2+c2-(6a)2=0,则3a2=c2,所以,故选C.
例9(2014年全国卷Ⅰ理4)已知F是双曲线C:x2-my2=3m(m>0)的一个焦点,则点F到C的一条渐近线的距离为( ).
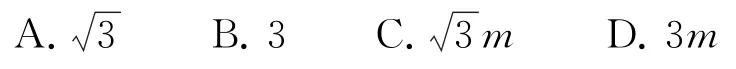
解析
例10(2017年江苏卷理8)在平面直角坐标系xOy中,双曲线的右准线与它的两条渐近线分别交于点P,Q,其焦点是F1,F2,则四边形F1PF2Q的面积是________.
解析
链接练习
1.(2018年江苏卷理8)在平面直角坐标系xOy中,若双曲线的右焦点F(c,0)到一条渐近线的距离为,则其离心率的值是________.
2.已知F1,F2是双曲线的左、右焦点,若点F1关于双曲线渐近线的对称点P满足∠OPF2=∠POF2(O为坐标原点),则C的离心率为( ).

3.已知双曲线的右焦点为F2,若C的左支上存在点M,使得直线bx-ay=0是线段MF2的垂直平分线,则C的离心率为( ).

4.已知F1,F2是双曲线的左、右焦点,渐近线分别为l1,l2,过点F1且与l1垂直的直线分别交l1及l2于P,Q两点,若满足则双曲线的渐近线方程为( ).
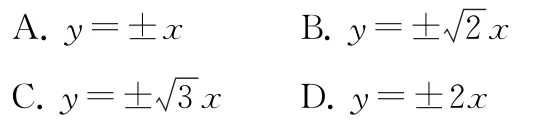
链接练习参考答案:
1.2.2.B.3.A.4.C.
