解析几何中的“三定”问题解法探究

◇ 山东 马 英 李冠兰

解析几何中的定值、定点、定线问题是历年高考或各地模拟考试中“常考常新”的热点问题,就2020年高考而言,全国卷Ⅰ(理科)和新高考卷都进行了考查.这类问题大多在解答之前并不知道定值是什么、定点在什么位置、有怎样的定直线,考试时遇到这类问题往往让考生望而生畏、倍感困惑.因此,归纳总结这类问题的题型特点和求解策略实属必要.

1 定值问题

解析几何中的定值问题是指某些几何量(线段的长度、图形的面积、角的度数、直线的斜率等)的大小或某些代数表达式的值和题目中的参数无关,不依参数的变化而变化,始终是一个确定的值.

解法探究选好参数,求出题目所需的代数表达式,然后对表达式进行直接推理、计算,并在推理计算的过程中消去变量,从而得到定值.这种方法可简记为:一选(选好参变量)、二求(对运算能力要求颇高)、三定值(确定定值).

例1已知椭圆的左、右焦点分别为F1,F2,|F1F2|＝2,M是椭圆E上的一个动点,且△MF1F2面积的最大值为.

(1)求椭圆E的标准方程;

(2)若A(a,0),B(0,b),四边形ABCD内接于椭圆E,AB∥CD,记直线AD,BC的斜率分别为k1,k2,求证:k1k2为定值.

解析

(1)设椭圆E的半焦距为c,由题意可知,当M为椭圆E的上顶点或下顶点时,△MF1F2的面积取得最大值所以故椭圆E的标准方程为.

直线AD的斜率为

直线BC的斜率为

所以

故k1k2为定值.

点评

本题第(2)问选“m”为参数,设出直线CD的方程与椭圆方程联立,设而不求分别表示出直线AD和直线BC的斜率,然后变形整理,整体消掉含有参数的式子得到定值.考查了考生分析、解决和整体处理问题的能力.

2 定点问题

解析几何中的定点问题是指直线过定点或曲线过定点问题,即不论直线或曲线中的参数如何变化,直线或曲线都经过某一个定点的问题.

解法探究定点问题的两种解法:一是从特殊入手,求出定点,再进行一般性的证明;二是把直线或曲线方程中的变量x,y当成常数看待,把相关的参数整理在一起,同时方程一端化为零.既然是过定点,那么这个方程就要对任意参数都成立,这时参数的系数就要全部等于零,这样就得到一个关于x,y的方程组,这个方程组的解确定的点就是直线或曲线所过的定点.

例2(2020年全国卷Ⅰ理20)已知A,B分别为椭圆的左、右顶点,G为E的上顶点为直线x＝6上的动点,PA与E的另一交点为C,PB与E的另一交点为D.

(1)求E的方程;

(2)证明:直线CD过定点.

解析

图1

(2)设P(6,y0),则直线AP的方程为y＝联立直线AP的方程与椭圆方程可得整理得

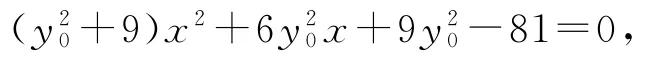
同理,可得点D的坐标为,所以直线CD的方程为

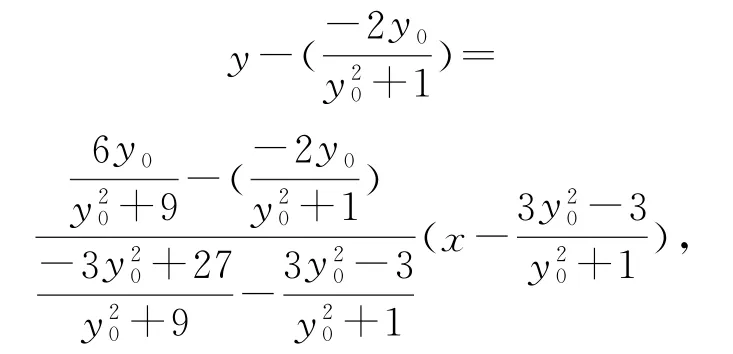
整理可得

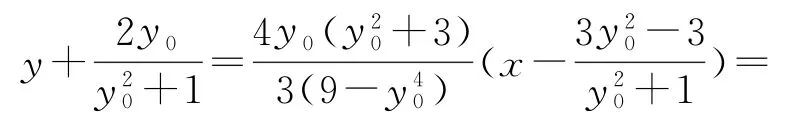
点评

本题第(2)问以点P的纵坐标为参数,得到直线AP的方程后与椭圆方程联立,整理变形后代入表示出点C和点D的坐标,进而表示出直线CD的方程,确定出与参数无关的定点.本题主要考查了椭圆的简单性质及方程思想的运用,考查了运算求解能力、推理论证能力及化归与转化思想.

3 定线问题

解析几何中的定线问题是指求证某动点不管如何变化,始终在某条直线上的问题,其本质就是求动点的轨迹方程.

解法探究定线问题是证明动点在定直线上,其实质是求动点的轨迹方程,所以所用的方法就是求轨迹方程的方法,如定义法、消参法、交轨法等.

例3已知椭圆C的方程为斜率为的直线l与椭圆C交于A,B两点,点在直线l的左上方.

(1)若以AB为直径的圆恰好经过椭圆C的右焦点F2,求此时直线l的方程;

(2)求证:△PAB的内切圆的圆心在定直线x＝1上.

解析

(1)设直线l的方程为y1),B(x2,y2).由得x2＋mx＋m2－3＝0,则x1＋x2＝－m,x1x2＝m2－3.

由Δ＝m2－4(m2－3)＞0,解得－2＜m＜2.又因为点在直线l的左上方,所以－2＜m＜1.若以AB为直径的圆恰好经过椭圆C的右焦点F2,则,即

化简得7m2＋4m－11＝0,解得或m＝1(舍),所以直线l的方程为.

点评

本题第(2)问是通过运算得到两条直线的斜率的和为0,说明直线x＝1平分∠APB,从而证明△PAB内切圆的圆心在定直线x＝1上.考查了分析、解决问题的能力和数形结合的数学思想.

4 综合应用

例4(2020年新高考卷22)已知椭圆的离心率为且过点A(2,1).

(1)求C的方程;

(2)点M,N在C上,且AM⊥AN,AD⊥MN,D为垂足.证明:存在定点Q,使得|DQ|为定值.

解析

(2)设点M(x1,y1),N(x2,y2).因为AM⊥AN,所以,即

当直线MN的斜率存在时,设方程为y＝kx＋m,如图2所示,代入椭圆方程消去y并整理得

所以

根据y1＝kx1＋m,y2＝kx2＋m,代入①整理得(k2＋1)x1x2＋(km－k－2)(x1＋x2)＋(m－1)2＋4＝0.

将②代入,得

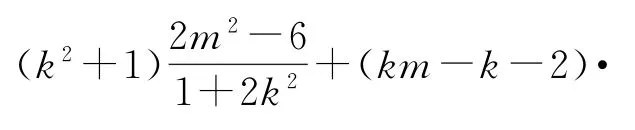
整理化简得(2k＋3m＋1)(2k＋m－1)＝0.

因为A(2,1)不在直线MN上,所以2k＋m－1≠0,2k＋3m＋1＝0,k≠1,于是MN的方程为,因此直线M过定点.

当直线MN的斜率不存在时,可得N(x1,－y1),如图3所示.代入式①可得(x1－2)2＋1－,解得x1＝2(舍)或,此时直线MN过点.

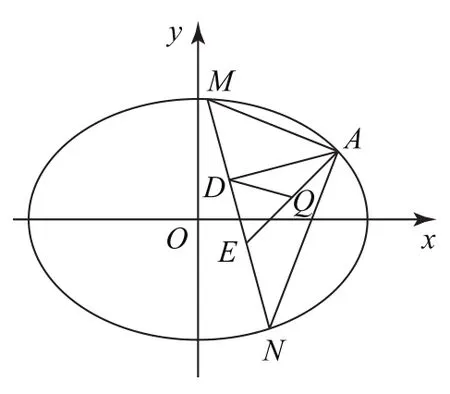
图2

图3

由于AE为定值,且△ADE为直角三角形,AE为斜边,所以AE中点Q满足|QD|为定值(AE长度的一半,即.

点评

本题第(2)问设出点M,N的坐标,在斜率存在时设方程为y＝kx＋m,联立直线方程与椭圆方程,根据已知条件,得到m,k的关系,进而可知直线MN恒过定点,在直线斜率不存在时要单独验证,然后结合直角三角形的性质即可确定满足题意的点Q的位置.本题考查了椭圆的标准方程和性质,是圆锥曲线中的定点、定值问题,特别是本题第(2)问在探索|DQ|为定值的基础上证明直线MN经过定点,并求得定点的坐标,考查了考生的理性思维和思维的灵活性、深刻性,方法的综合性、探究性和创造性等.本题对考生的数学思维能力提出了较高的要求,要求考生具备解决较复杂问题的综合素养和能力.