基于多维度LSTM模型的短时交通流预测
2020-12-15陈治亚王小军
陈治亚,王小军
基于多维度LSTM模型的短时交通流预测
陈治亚,王小军
(中南大学 交通运输工程学院,湖南 长沙 410075)
提出一种基于长短时记忆神经网络(Long Short-Term Memory,LSTM)的交通流预测模型,不同于单一因素预测,模型深入探究时间占有率等因素对预测结果的影响,从而进行多维度的短时交通流预测。最后以长沙市某实地数据对模型预测结果的精确性进行检验。研究结果表明:在以10 min为间隔预测中,与时间占有率组合的多维度因素速度预测和流量预测的平均绝对误差相较单一因素分别由4.6 km/h降至2.78 km/h,9.65辆降至5.8辆。加入时间占有率等其他因素后,模型预测的精度显著提高。
智能交通;交通流预测;LSTM;神经网络
随着经济社会的高速发展,由城市交通供给与需求的不平衡导致的交通拥堵等城市交通问题日益严重。智能运输系统是解决城市道路交通拥堵问题,提高道路通行率的有效途径[1]。智能交通系统的核心问题在于实现交通控制与诱导,而短时交通流的实时预测是实现科学管控的必要前提。随着交通流预测领域研究的深入,学者们提出了许多交通流预测模型和方法,常用的预测模型大致可以分为传统预测模型和神经网络预测模型。前者有Ahmaed等[2]首次将自回归积分移动均值法(Auto- gression-integrated MA,AIRMA)模型应用于高速公路交通流预测;Mascha等[3]将ARIMA模型应用于短时交通流预测的研究中,同时还考虑了交通流时间序列中的相关性;Brian等[4]使用季节性ARIMA模型对高速公路进行短时交通流预测,并比较在不同时间间隔预测效果的优劣;Gary等[5]应用时间序列模型预测了高速公路交通流的变动趋势,实验证明该模型具有较好的鲁棒性,即能在少量间断的交通流数据中有一个较不错地应用。GUO等[6]利用随机的自适应卡尔曼滤波模型进行交通流预测并取得了良好的效果。对于传统模型来说,由于交通流内在的非线性和非平稳特性,往往会导致预测精度降低,模型抗干扰能力差。而人工神经网络非常擅长处理大数据,加上其强大的学习能力和自适应能力,被广泛应用于交通预测中。姚加林等[7]研究了在数据缺失情况下用K近邻(KNN)算法预测路网中各路段速度。张利等[8]基于粗糙集和遗传算法,提出了一种改进的BP神经网络算法,提高了模型的训练精度和泛化能力;董春娇等[9]在空间层面上重新划分了道路网,重构交通流时间序列,用新序列作为输入向量,用Elman神经网络实现道路网多断面同时预测;李巧茹等[10]将支持向量机(SVM)和时空数据相融合,构建了更为精确的交通流预测模型;赵亚萍等[11]基于最小二乘支持向量机的交通流预测模型,通过实例验证了模型具有学习速度快、跟踪性能好以及泛化能力强等优点;谭娟等[12]在归纳基础数据构建交通流特征向量并确定4种预测状态之后,采用深度学习的自编码网络进行无标签训练,最后在顶层搭建Softmax回归模型对交通拥堵状况进行多态预测;罗向龙等[13]利用差分技术消除交通流数据中的趋势向,结合深度信念网络和支持向量回归进行预测;Nicholas等[14]针对交通流预测提出了一种新型的深度学习结构,它包含了L1正则化的线性模型以及一系列tanH网络层;对于传统的递归神经网络,它无法训练具有较长时间间隔的时间序列,并且存在梯度爆炸或消失。为了解决这些缺点,Hochreiter等[15]提出了长期短期记忆神经网络(LSTM NN)。MA等[16]运用LSTM来预测交通速度,发现它可以捕获时间序列中的时间特征,适用于交通预测,且在交通预测中具有良好的性能。深度学习正处于一个飞速发展的时期,并在短时交通流预测领域中得到广泛的应用。但现有的研究成果,依然存在一些不足,现有文献在特征变量的选取过程中,通常仅以单一变量对交通流进行预测,忽略多个因素对于交通流的影响,导致预测结果精度不高。针对现有研究的不足,本文提出基于深度学习的理论框架,构建LSTM的交通流预测模型,利用python语言和keras平台来进行实现,将原始数据处理成五段不同的时间间隔,分析在不同时间周期下的预测结果的情况;提出状态变量的概念,将交通流量、速度以及时间占用率等多个因素组合成多维度状态变量作为输入向量,输入到训练好的LSTM预测模型中,并将同样的数据输入到其他不同的预测算法,通过计算误差评价指标来对比验证预测结果。
1 基于LSTM的交通流预测模型
交通流通常具有随机性,流量及速度等相关参数经常受道路实际路况、交通管制等因素的影响,从而呈现出非线性的特点,给交通流预测工作带来极大的困难。长期短时记忆神经网络具有准确度高、分布存储以及学习能力强等优势,其对噪声神经有较强的鲁棒性和容错能力,能充分逼近复杂的非线性关系,同时还具备联想记忆的功能,从而可以有效地处理时间序列问题。因此,LSTM是一种理想的交通流预测模型。
1.1 LSTM
长期短时记忆神经网络(Long Short-Term Memory, LSTM)是一种特殊的递归神经网络结构,具有与其他方法相同的基本结构(一个输入层,一个循环隐藏层和一个输出层),它们之间的区别是隐藏层。LSTM的主要创新是由存储单元组成的隐藏层。存储单元是一种强大的结构,可以通过一些记忆单元来确定信息的状态并将其存储,主要包括输入门,遗忘门和输出门。应用输入门以激活新的输入信息并控制需要更新的信息;遗忘门确定丢弃最后一刻的细胞状态信息量;输出门控制可以导出当前单元状态的哪些信息。
设输入序列为(1,2,…,x),隐藏层状态为(1,2,…,h),则在时刻有:
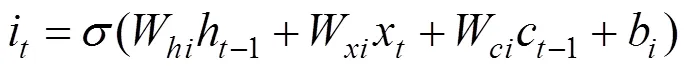
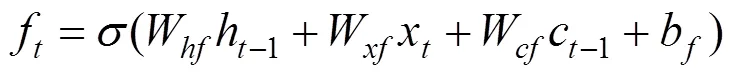
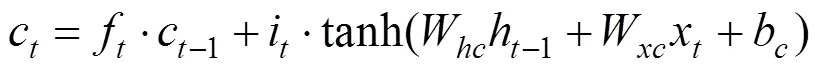
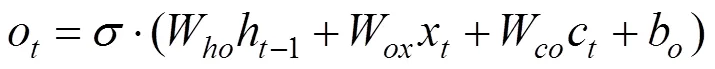
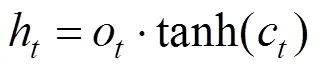

1.2 状态变量
传统的交通流预测模型大多考虑单因素对预测结果的影响,而忽略了道路上其他因素。本文在构建了5种不同维度的状态变量,,,和,其中状态变量为只包含速度因素,和在速度维度的基础上还分别加上了交通流量和时间占有率;状态变量为只包含流量因素,是在流量维度的基础上分别加上了时间占有率。
1.3 交通流预测模型
本文考虑不同的因素对预测的影响,故将不同的状态变量作为输入值,构建短时交通流预测模型,具体建模过程如下所示。
1) 选择实验数据并进行数据预处理
读取实验所需的数据,并进行数据降噪及归一化处理,构建状态变量,确定数据的训练集和测试集,根据不同的状态变量确定不同输入向量。
2) 确定LSTM模型的参数
根据经验和多次试验设置调整模型的超参数,包括网络层数、隐含层节点数、激励函数、目标函数、优化函数以及迭代次数等。
3) LSTM模型的训练
将权值矩阵和偏置随机化,在输入层中导入输入向量,计算第一层隐含层的输入门、遗忘门、输出门的输入向量和输出向量以及记忆单元的输入向量和状态值,得到记忆模块的输出向量,并将其作为下一层隐含层的输入向量,以此类推,得到预测值。根据其预测值计算误差函数,将误差反向传播进行权值更新,达到最大迭代数时结束训练。
4) 预测并分析
将训练好的模型进行预测,得到最终的预测结果,并通过误差评价指标与实际数据进行对比 分析。
2 实例分析
2.1 数据来源
本文选取湖南省长沙市某路段交通检测器数据,由官方提供的历史监控数据进行处理得到的实验样本。该数据包括的某点的每隔一分钟的交通流量,速度以及时间占有率,根据预测模型的特征需要,选取较完整的数据,数据集为2012-09-03~2012-09-14,共11 d,其中训练数据集为前10 d,最后一天的数据作为测试的数据集。
2.2 数据预处理
由于原始数据中存在缺失值,所以考虑用相邻数据取均值的方式进行处理。同时为了测试不同时间周期对模型影响,将交通流量进行求和,速度和时间占有率进行取均值处理,分别将数据处理成3,5,10以及15 min数据。为了消除不同量纲的影响,将实验要用到的交通流数据按式(6)进行归一化 处理。
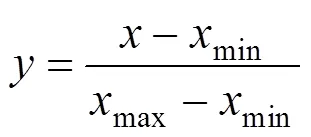
式中:代表归一化后的值;代表原始值,max和min分别代表原始数据中的最大值和最小值。
2.3 误差评价指标及参数
为了评价模型的预测结果,本文分别以平均绝对误差(MAE)和平均绝对百分误差(MAPE)作为评价指标,即:
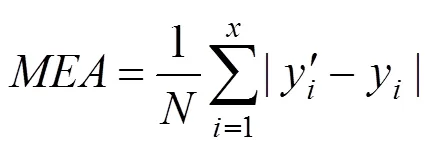
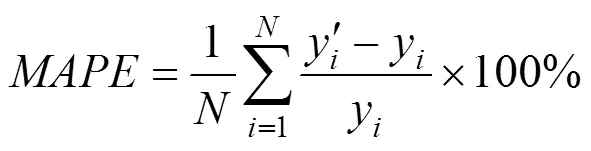
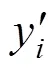
本文算法在python3.6环境下,利用Keras深度学习库建立交通流预测模型,其中,根据经验和通过多次实验测试和调参,将模型隐含层数设为3层,3层隐含层的节点数分别设为32,32和16;在LSTM中,ReLU函数为最常用的激活函数,目标函数为MSE,,优化函数为adam函数。
2.4 实验结果及分析
本文将原始的交通流数据分别处理成5种不同的时间间隔,分别将1,3,5,10和15 min的交通速度的数据来进行预测。预测结果如表1所示。
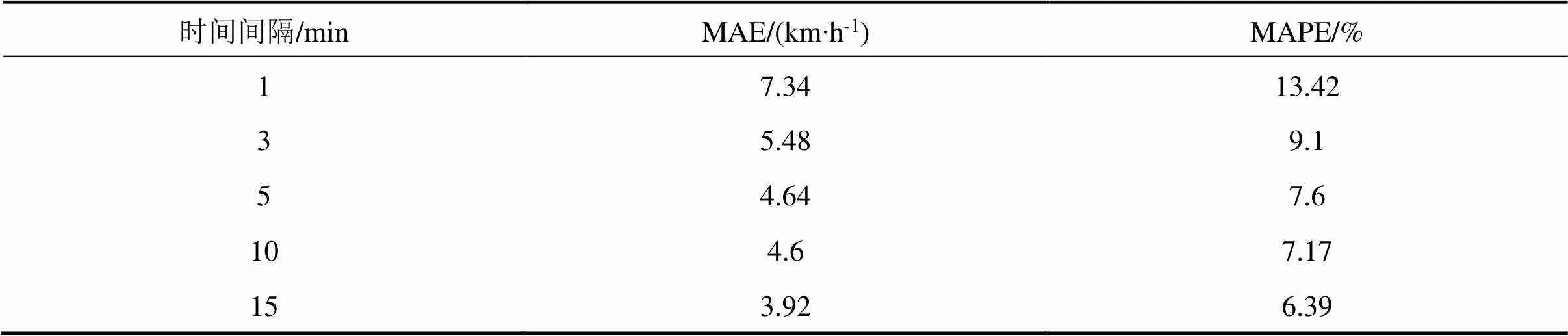
表1 不同时间间隔下的交通速度预测结果
由表1可以看出本文用到的方法得到的预测值和真实值之间有着很好的拟合效果。但对10 min和15 min为时间间隔的状态变量包含的信息最多,预测效果相对最好,预测值的平均绝对误差分别为4.6 km/h和3.92 km/h;预测效果其次是时间间隔3 min和5 min,预测结果的平均绝对误差分别为5.48 km/h和4.64 km/h;而当时间间隔1 min的状态变量信息最少,且交通流数据的波动性较大,稳定性也很差,预测效果最差,预测结果的平均绝对误差为7.34 km/h。对比5种不同时间间隔的预测效果,由此可以得出结论:在短时交通流预测,输入向量的时间间隔越大,预测的精度相对就越高。
实验将不同的状态变量作为输入向量,即除了速度因素之外的,还分别加入了相对应的流量和时间占有率对预测的影响。经过多次预测实验,预测结果如表2所示。
由表2可以看出,在不同时间间隔下,对比只考虑交通速度的状态变量,加入交通流量或时间占有率的状态变量和预测精度有进一步的提高,其中以10 min的预测结果最好。

表2 不同状态变量的交通速度预测平均绝对误差对比
注:状态变量为速度变量,状态变量为速度变量和流量变量,状态变量为速度变量和时间占有率变量。
图1,图3和图5分别为10 min下3个状态变量LSTM模型预测结果和真实值的对比,加入流量因素的状态变量和加入时间占有率状态变量的预测效果会比只考虑速度的状态变量的更好,和真实值的拟合度更好,相对应的平均绝对误差分别为2.97 km/h和2.78 km/h。其中考虑时间占有率的状态变量预测结果会更好。
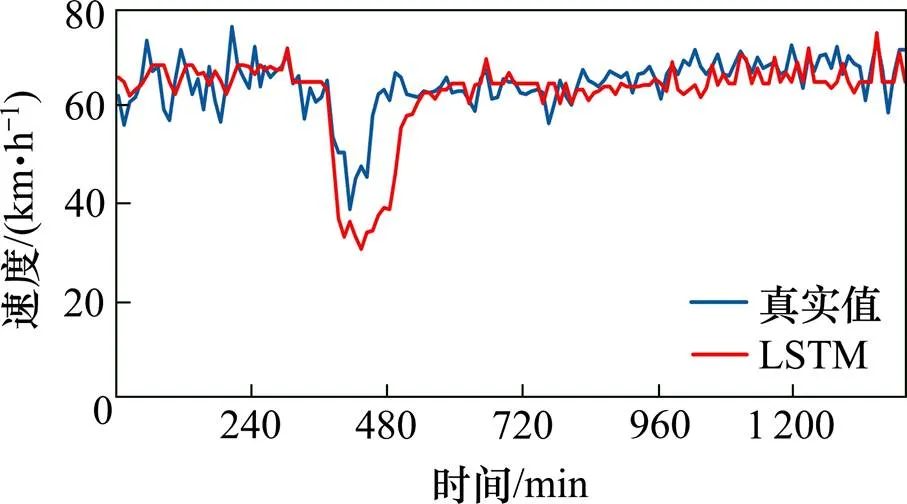
图1 状态变量A速度预测结果对比图
10 min下3个状态变量预测的误差分布图如图2,图4和图6所示。状态变量误差占比最高是(-6,-2),为34.53%,而在状态变量和状态变量中均为(-2,2),分别为49.48%和51.8%。3种状态变量在对于误差绝对值大于6的占比分别为21.59%,13.66%和12.94%。
用同样的思路对交通流量进行预测,输入向量在考虑流量的同时,分别加上速度和时间占有率探究多维度因素对流量预测的影响。经过多次实验,间隔为10 min的预测效果最好。所以用10 min的数据进行流量预测,预测结果如表3所示。
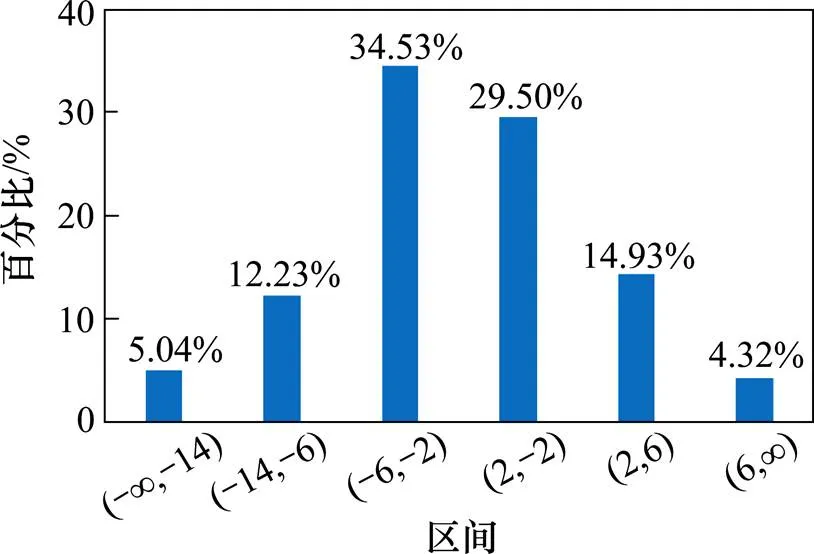
图2 状态变量A速度预测误差分布图
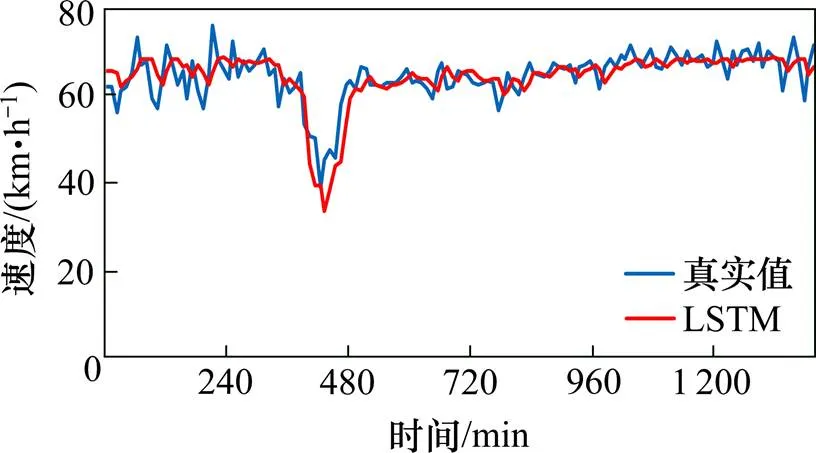
图3 状态变量B速度预测结果对比图
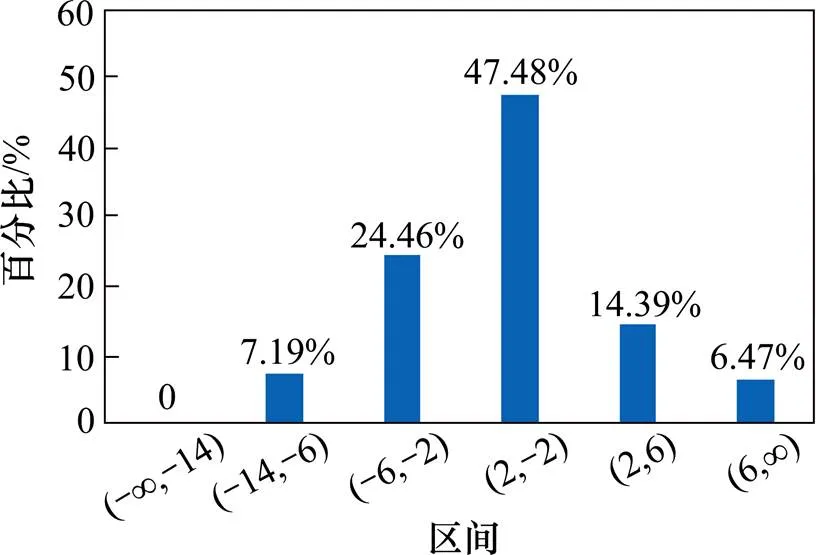
图4 状态变量B速度预测误差分布图
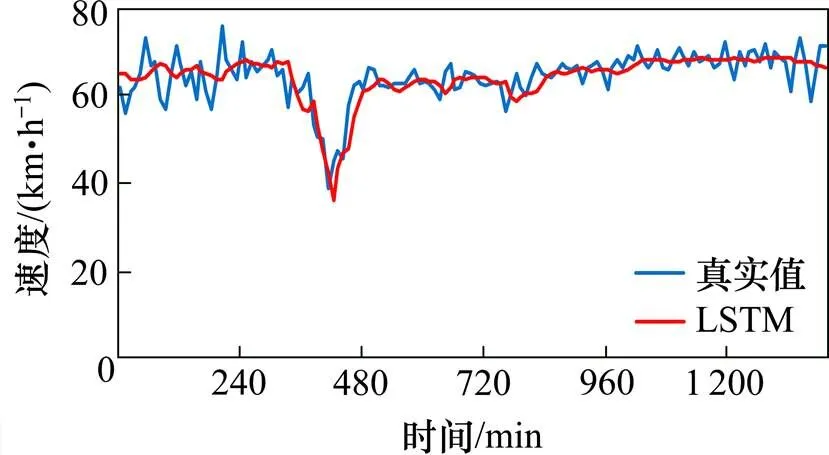
图5 状态变量C速度预测结果对比图

图6 状态变量C速度预测误差分布图

表3 不同状态变量的交通流量预测结果对比
注:状态变量为流量变量,状态变量为流量变量和时间占有率变量。
图7,图8和图9分别是在10 min下3个状态变量LSTM模型流量预测值和真实值的对比,可以看出,状态变量和状态变量的预测拟合度更好,相对应的平均绝对误差分别为6.8辆和5.8辆。其中考虑时间占有率的状态变量预测结果会更好,在(-9,9)误差范围占比为82.22%,状态变量预测的误差分布图如图10所示。
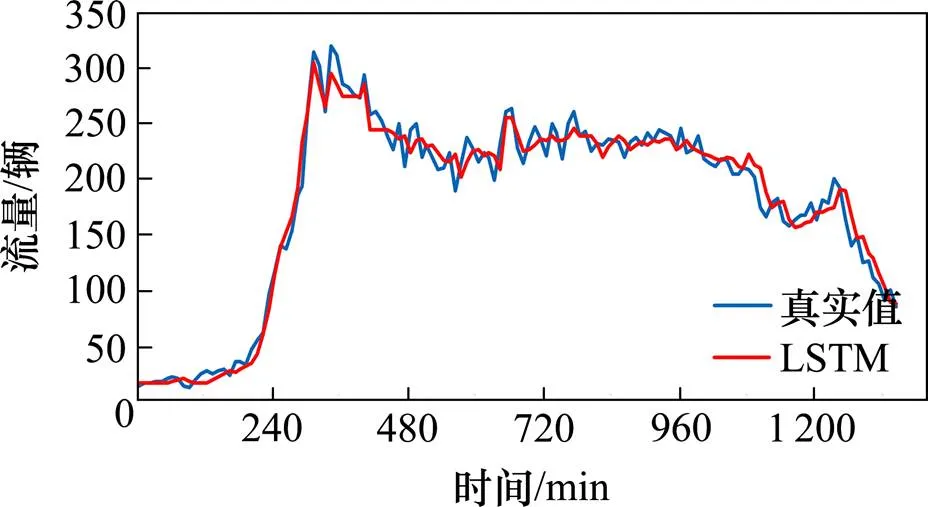
图7 状态变量D流量预测结果对比图
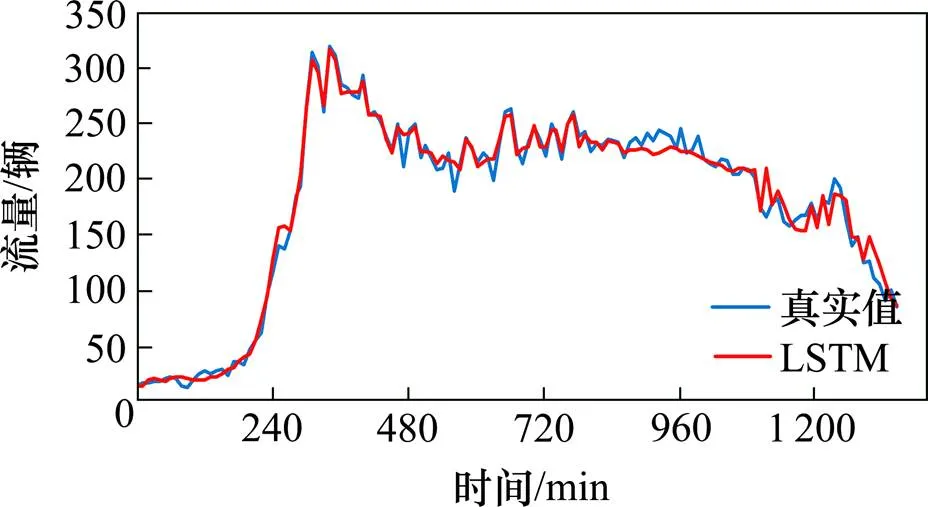
图8 状态变量B流量预测结果对比图
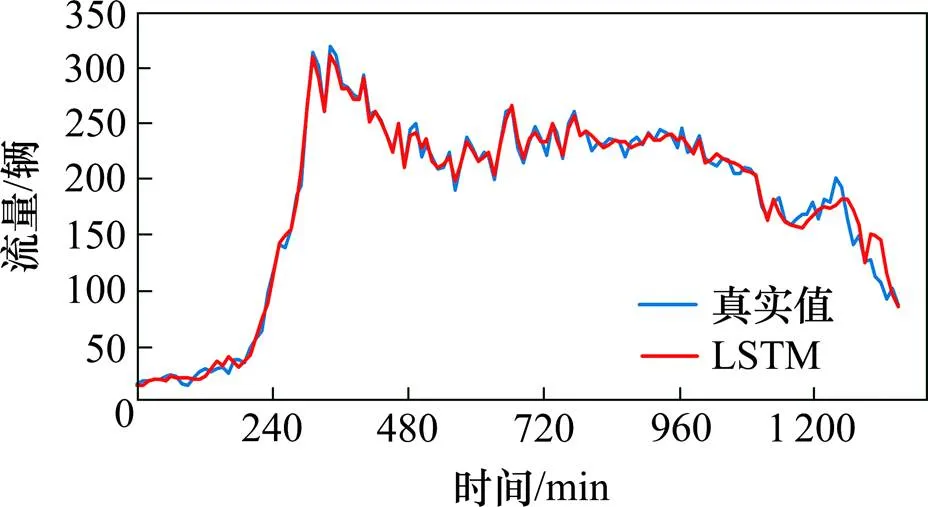
图9 状态变量E流量预测结果对比图
同时,为了验证LSTM预测精度的可靠性,本文通过ADA,随机森林(Random Forest, RF),ER随机网络以及多层感知器(Multi-layer Perception MLP)4种模型作为对比,因为10 min的预测效果相对最好,所以考虑使用10 min的数据,实验对比结果如表4所示。
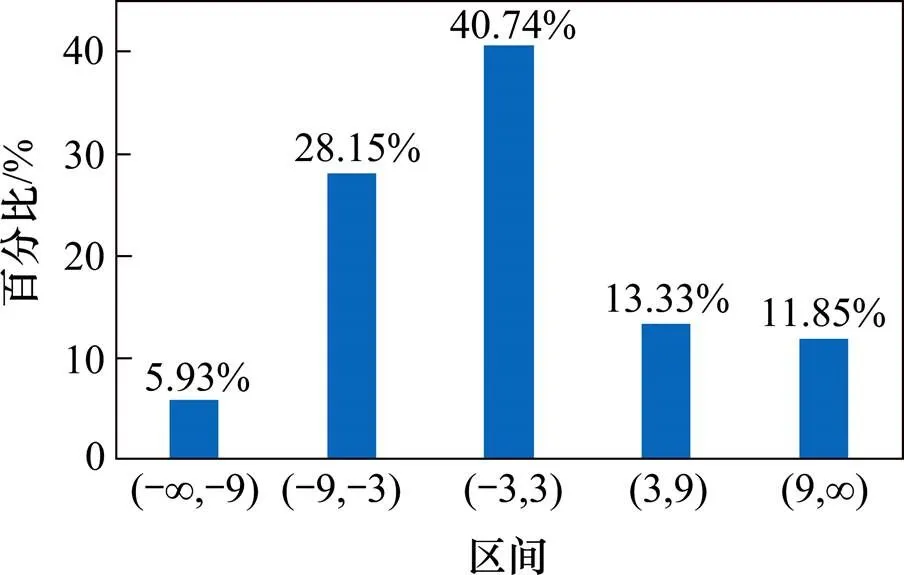
图10 状态变量E流量预测误差分布图
由表4可以看出,在10 min的时间间隔中,考虑速度和时间占有率的LSTM神经网络预测的MAE,MAPE分别为2.78 km/h,4.47%,预测准确率高达95.5%。无论是只考虑速度因素状态变量,还是加上流量和时间占有率的状态变量和状态变量,LSTM模型的平均绝对误差分别为4.6,2.97和2.78 km/h,相对其他4种不同的模型来说,MAE和MAPE都更小,预测精度最高。
3 结论
1) 对于5种不同的时间间隔下的交通流预测,发现10 min的预测效果最好。
2) 在速度预测中,由速度和时间占有率组合的状态变量预测效果最佳;在流量预测中,由流量和时间占有率组合的状态变量预测效果最佳。
3) 对比不同的预测方法,发现具有记忆功能的LSTM模型在短时交通流预测中表现最好,预测的精度最高。
[1] 罗向龙, 李丹阳, 杨彧, 等. 基于KNN-LSTM的短时交通流预测[J]. 北京工业大学学报, 2018, 44(12): 1521-1527. LUO Xianglong, LI Danyang, YANG Yu, et al. Short- term traffic flow prediction based on KNN-LSTM[J]. Journal of Beijing University of Technology, 2018, 44(12): 1521-1527.
[2] Ahmaed Mohamed S, Cook Allen R. Analysis of freeway traffic time-series data by using Box-Jenkins technique [J]. Transportation Research Record 722, 1979: 1-9.
[3] Mascha Van Der Voort, Mark Dougherty, Susan Watson. Combining kohonen maps with arima time series models to forecast traffic flow[J]. Transportation Research Part C, 1996, 4(5): 307- 318.
[4] Brian L Smith, Billy M Williams, R Keith Oswald. Comparison of parametric and nonparametric models for traffic flow forecasting[J]. Transportation Research Part C, 2002,10(4): 303-321.
[5] Gary A Davis, Nancy L Nihan. Using time-series designs to estimate changes in freeway level of service, despite missing data[J]. Pergamon, 1984, 18(5-6): 431- 438.
[6] GUO Jianhua, HUANG Wei, Billy M. Williams. Adaptive Kalman filter approach for stochastic short-term traffic flow rate prediction and uncertainty quantification[J]. Transportation Research Part C, 2014, 43: 50-64.
[7] 姚加林, 朱闯. 数据缺失环境下基于DCTPLS-PCA的路网速度预测研究[J]. 铁道科学与工程学报, 2019, 16(10): 2612-2619. YAO Jialin, ZHU Chuang. Research on road network speed prediction based on DCTPLS-PCA in data loss environment[J]. Journal of Railway Society and Engineering, 2019, 16(10): 2612-2619.
[8] 张利, 吴华玉, 卢秀颖. 基于粗糙集的改进BP神经网络算法研究[J]. 大连理工大学学报, 2009, 49(6): 971- 976. ZHANG Li, WU Huayu, LU Xiuying. Research on improved BP neural network algorithm based on rough sets[J]. Journal of Dalian University of Technology, 2009, 49(6): 971-976.
[9] 董春娇, 邵春福, 熊志华, 等. 基于Elman神经网络的道路网短时交通流预测方法[J]. 交通运输系统工程与信息, 2010, 10(1): 145-151. DONG Chunjiao, SHAO Chunfu, XIONG Zhihua, et al. Short-term traffic flow prediction method of road network based on Elman neural network[J]. Journal of Transportation Systems Engineering and Information Technology, 2010, 10(1): 145-151.
[10] 李巧茹, 赵蓉, 陈亮. 基于SVM与自适应时空数据融合的短时交通流量预测模型[J]. 北京工业大学学报, 2015, 41(4): 597-602. LI Qiaoru, ZHAO Rong, CHEN Liang. Short-term traffic flow prediction model based on SVM and adaptive spatiotemporal data fusion[J]. Journal of Beijing University of Technology, 2015 41(4): 597-602.
[11] 赵亚萍, 张和生, 周卓楠, 等. 基于最小二乘支持向量机的交通流量预测模型[J]. 北京交通大学学报, 2011, 35(2): 114-117, 136. ZHAO Yaping, ZHANG Hesheng, ZHOU Zhuonan, et al. Traffic flow prediction model based on least squares support vector machine[J]. Journal of Beijing Jiaotong University, 2011, 35(2): 114-117, 136.
[12] 谭娟, 王胜春. 基于深度学习的交通拥堵预测模型研究[J]. 计算机应用研究, 2015, 32(10): 2951-2954. TAN Juan, WANG Shengchun. Research on traffic congestion prediction model based on deep learning[J]. Application Research of Computers, 2015, 32(10): 2951- 2954.
[13] 罗向龙, 焦琴琴, 牛力瑶, 等. 基于深度学习的短时交通流预测[J]. 计算机应用研究, 2017, 34(1): 91-93, 97. LUO Xianglong, JIAO Qinqin, NIU Liyao, et al. Short- term traffic flow prediction based on deep learning[J]. Applied Computer Research, 2017, 34(1): 91-93, 97.
[14] Nicholas G Polson, Vadim O Sokolov. Deep learning for short-term traffic flow prediction[J]. Transportation Research Part C, 2017, 19: 1-17.
[15] Hochreiter S, Schmidhuber J. Long short-term memory[J]. Neural Computation, 1997, 9(8): 1735-1780.
[16] MA Xiaolei, TAO Zhimin, WANG Yinhai, et al. Long short-term memory neural network for traffic speed prediction using remote microwave sensor data[J]. Transportation Research Part C, 2015, 54: 187-197.
Short-term traffic flow prediction based on multi-dimensional LSTM model
CHEN Zhiya, WANG Xiaojun
(School of Traffic and Transportation Engineering, Central South University, Changsha 410075, China)
Different from single-factor prediction, a traffic flow prediction model based on Long Short-Term Memory was developed to explore the influence of time occupancy and other factors on the prediction results, so as to conduct multi-dimensional short-term traffic flow prediction. A real-world traffic data in Changsha was used to test the accuracy of the model. The results show that in the 10-minute interval prediction, compared with the single-dimensional model, the MAE of the speed in the multi-dimensional model can be substantially reduced from 4.6 km/h to 2.78 km/h, and that of volumes from 9.65 to 5.8. Therefore, taking other factors as time occupancy into consideration can significantly improve the accuracy of the traffic prediction models.
intelligent transportation; traffic flow prediction; LSTM; neural network
U491
A
1672 - 7029(2020)11 - 2946 - 07
10.19713/j.cnki.43-1423/u.T20200023
2020-01-10
湖南省自然科学基金资助项目(2018JJ2537)
陈治亚(1958-),男,湖南岳阳人,教授,博士,从事交通运输规划与管理;E-mail:chzy@csu.edu.cn

(编辑 阳丽霞)
