轨道精度对中低速磁浮列车-轨排-桥梁动力作用影响
2020-12-15敖建安魏高恒马卫华周策罗世辉于尧
敖建安,魏高恒,马卫华,周策,罗世辉,于尧
轨道精度对中低速磁浮列车-轨排-桥梁动力作用影响
敖建安1,魏高恒2,马卫华3,周策3,罗世辉3,于尧4
(1. 中车大连机车车辆有限公司,辽宁 大连 116022;2. 中铁第四勘察设计院集团有限公司,湖北 武汉 430063;3. 西南交通大学 牵引动力国家重点实验室,四川 成都 610031;4. 中南大学 轨道交通安全教育部重点实验室,湖南 长沙 410075)
针对以往研究中用少量集中力模拟电磁铁悬浮力的不足,推导悬浮力理论计算公式并通过有限元方法分析悬浮力建模。以新型中低速磁浮列车、某磁浮旅游线25 m简支梁为研究对象,建立新型中低速磁浮列车-轨排-桥梁耦合动力学模型,对比不同磁浮力元数量的磁浮列车的动力学计算结果,研究不同的轨排前后高低(10 m弦矢高)和轨排接缝允许偏差(垂向)对系统动力作用的影响。研究结果表明:用数个悬浮力元模拟悬浮力在工程实际中是可行的,其中三力元模型计算速度较快精度较高;轨排前后高低(10 m弦矢高)对列车运行平稳性影响较大,轨排接缝允许偏差(垂向)对悬浮间隙、悬浮架最大垂向加速度影响较大,轨排接缝允许偏差(垂向)允许偏差应该控制在±2 mm以内。
新型中低速磁浮;悬浮力;轨道几何;轨排;梁;动力学仿真
磁浮列车是21世纪极具竞争力的无接触地面有轨交通工具。中低速常导磁浮列车环抱轨道运行,结构上避免了列车脱轨的风险,具有更高的安全性、良好的乘坐舒适性、低噪音低排放、爬坡能力强、曲线通过性能好等优点[1-3],其中新型中低速磁浮列车相比传统HSST型中低速磁浮列车有更低的动力作用和更高的速度[4],有更好的运用前景。由于中低速磁浮列车对轨道不平顺较为敏感,而轨道不平顺的重要来源之一是轨道结构几何误差,许多研究表明引起轨道结构几何误差的主演因素包括F轨表面不平顺、相邻F轨不对中、施工误差、支撑沉降等[5-6],由于轨道结构几何误差是轨道本身的固有属性,因此在磁浮列车动力学建模时须要考虑轨排的影响。CAI等[7-8]提出了考虑弹性轨道的车-桥耦合动力学模型,研究了车体垂向加速度、电磁铁数量、列车体个数及速度对轨道变形和列车动力学特性的影响。曾佑文等[9]建立了三节编组磁浮列车动力学模型,使用弹簧阻尼等效悬浮力,伯努利欧拉梁模拟轨道梁,研究表明悬浮模块对于轨道不平顺较为敏感,特别是梁跨交界处的不连续对模块响应极为有害。赵春发[2]根据青城山中低速磁浮试验车建立了35自由度动力学模型,磁轨关系考虑了反馈控制的动态磁轨关系,分析得到了电磁悬浮力及其动态刚度和阻尼特性。SHI等[10]建立的高速磁浮车-线耦合动力学模型考虑了线路条件、电磁控制、轨道梁空间振动等因素,对轨道梁垂向共振、车线随机振动、曲线通过性能进行了初步分析计算。梁鑫等[11]研究了单铁悬浮车-桥耦合振动,将悬浮系统、车辆、柔性轨道梁作为一个整体,并以不同的外激扰模拟磁浮列车不同速度下对桥梁的作用,分析了不同梁型的跨中挠度和振动加速度变化。Kim等[12]使用模态叠加法将柔性梁和采用反馈控制的悬浮电磁铁加入车辆-桥梁动力学模型中,通过动力学仿真进行了失稳现象的分析和悬浮间隙控制性能的研究。汪科任等[13]利用SIMPACK软件建立了56自由度的新型中低速磁浮车辆动力学模型进行仿真计算,利用单悬浮架试验台进行了乘坐舒适性试验验证,证明了新型中低速磁浮车辆有较好的动力学性能。任晓博[14]以长沙磁浮快线25 m双线简支梁和中低速磁浮车辆利用ANSYS建立了中低速磁浮车辆-轨道-桥梁耦合动力学模型,并开展了动力作用研究。但是现有研究中都将悬浮力考虑为少量集中力,但是如此模拟悬浮电磁铁线圈悬浮力的磁浮车辆动力学模型在轨道短波激励仿真计算中有其局限性[15],且车-线耦合模型中很少考虑轨排的影响。本文以新型中低速磁浮列车、某磁浮旅游线25 m简支梁为研究对象,分析了悬浮电磁铁悬浮力理论计算公式和有限元计算结果,研究了悬浮电磁铁悬浮力的悬浮力元建模方法,建立了新型中低速磁浮列车-轨排-桥梁耦合动力学模型。分析对比了不同磁浮力元数量的磁浮列车的动力学计算结果,并研究了不同的轨排前后高低(10 m弦矢高)、轨排接缝允许偏差(垂向)对系统动力作用的影响。
1 悬浮力建模
悬浮系统包括悬浮控制系统与悬浮电磁铁两部分。悬浮控制系统是控制悬浮电磁铁电流以调整悬浮力保持悬浮稳定的系统。中低速磁浮车辆的悬浮电磁铁通过吸附F形铁磁轨道的磁极,实现列车的悬浮和导向。
1.1 悬浮力计算公式
单点悬浮常用如图1所示的单铁悬浮模型,图中及后继所示公式中符号如下:为悬浮间隙,0为真空磁导率,为磁极正对面积,为线圈绕组匝数,为线圈绕组电流。悬浮力的计算在满足工程应用精度的情况下做如下假设:

图1 单铁悬浮模型
1) 全部磁阻R等于气隙磁阻:
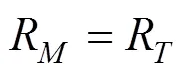
气隙磁阻:

2) 铁芯磁通Ф等于气隙磁通:

气隙磁通:

则,计算磁通密度为:
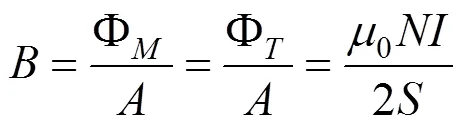
计算磁能为:
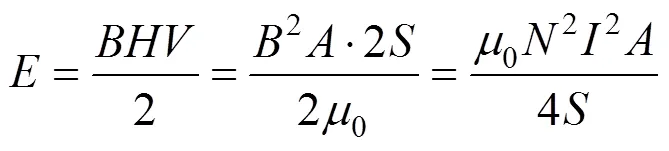
计算悬浮电磁力为:

悬浮电磁力和磁通密度的关系为:

其中:和0是常量,可知悬浮电磁力和间隙磁通密度的平方成正比。
1.2 磁通密度仿真
由于电磁铁和F轨材料的非线性导磁特性和气隙之间的漏磁等因素的影响,很难用解析方法求解电磁场的特性,所以采用离散化的有限元技术对悬浮电磁铁、F轨之间的电磁场进行分析。其有限元模型如图2所示,部分参数如表1所示。

表1 电磁分析模型部分参数表

图2 悬浮电磁铁与F轨有限元模型
悬浮电磁铁纵向气隙磁通密度如图3所示,图中黑色曲线为悬浮电磁铁内外侧极板磁通密度平均值,红色直线为气隙磁通密度平均值为0.81 T(特斯拉),2个悬浮电磁铁线圈位置处的磁通密度和平均磁通密度的偏差小于5%。
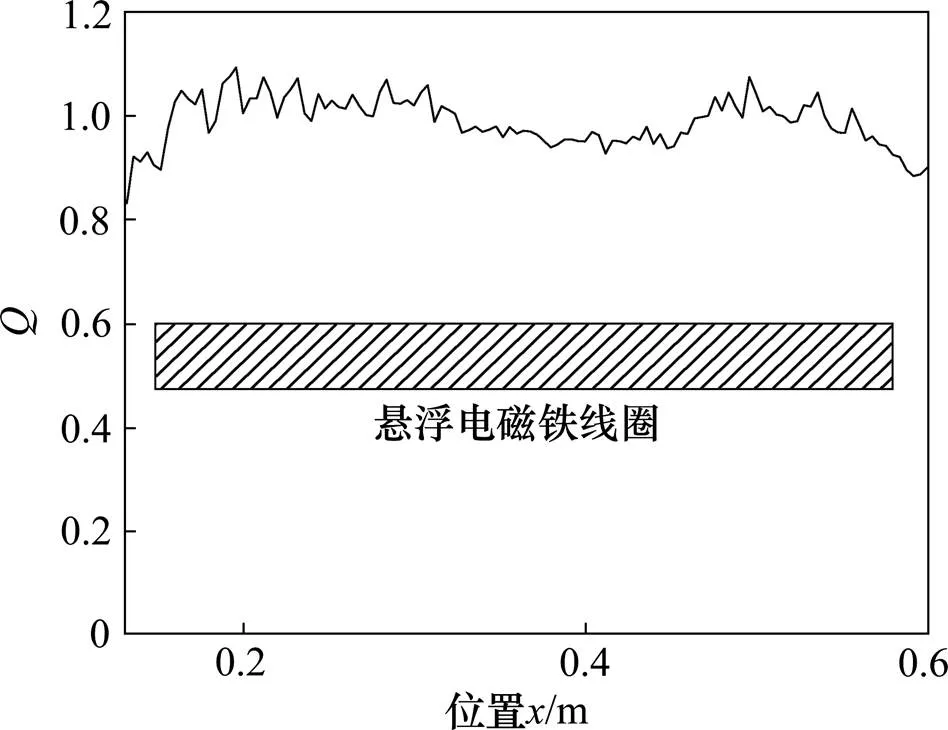
图4 比值Q
1.3 悬浮力简化建模方法
根据式(8)和仿真得到的气隙磁密,可以得到各点位置的悬浮力和平均悬浮力,为了明确悬浮电磁铁各个位置上提供的悬浮力和平均悬浮力的关系,定义悬浮力和平均悬浮力的比值:

由图4可见,悬浮力和平均悬浮力比值的值在一个悬浮电磁铁线圈长度上在1附近波动,最大偏差不超过10%,说明悬浮电磁铁线圈各位置提供的悬浮力大小基本相等,这一结果为将电磁悬浮力进一步简化为数个集中力元提供了一定的依据。
根据式(8),理论上可以认为悬浮电磁铁线圈各处的磁通密度为定值,则可将一个悬浮模块的悬浮电磁铁划分为段,得到电磁铁的电磁悬浮合力:

式(10)中:的取值越大则悬浮电磁铁线圈电磁力的计算越精确,后续将对的取值进行讨论。
2 列车-轨排-桥梁耦合动力学模型
2.1 列车动力学模型
本文基于多刚体动力学软件Universal Mechanism(Universal Mechanism是俄罗斯布良斯克理工大学开发的一款多体系统动力学建模和仿真计算软件,其中有专门针对磁浮列车开发的磁浮模块,计算精度和速度较好,下称UM)建立了新型中低速磁浮列车动力学模型,如图5所示。
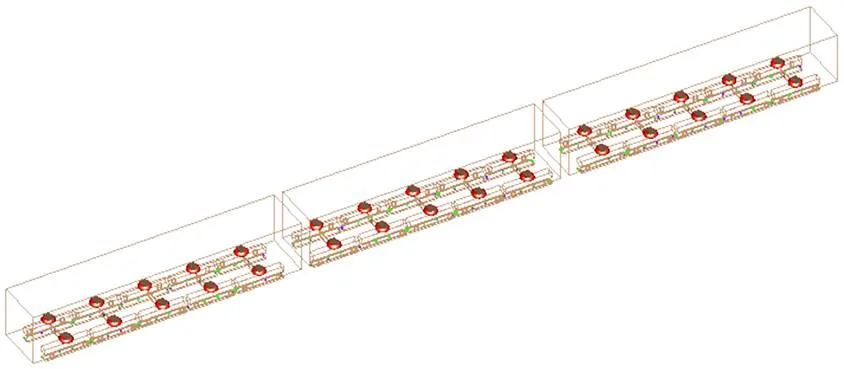
图5 新型中低速磁浮列车动力学模型
部分建模参数见表2。其中悬浮力建模根据上文所述,分别取=1,3,5,即在UM软件中采用1,3,5个的Maglev悬浮力元对悬浮电磁铁线圈悬浮力建模。

表2 新型中低速磁浮列车动力学参数
建立的新型中低速磁浮列车动力学模型主要包括3个车体和15个悬浮架,共包括258个自 由度。
2.2 轨排-桥梁动力学模型
本文轨排-桥梁耦合模型以某中低速磁浮旅游专线为研究对象,其中轨道结构由轨排、扣件和承轨台组成[16],轨道梁多采用跨距25 m标准简支梁。利用有限元软件ANSYS分析中低速磁浮轨排与桥梁结构有限元模型,如图6所示。
F轨采用三维8节点实体单元Solid 185建模;工程实际中在F轨轨缝处采用Ⅰ型伸缩接头连接2根F轨,因此在轨缝相邻F轨处设置具有垂向刚度的Combin 14弹簧单元来模拟Ⅰ型伸缩接头对F轨的支撑作用,刚度设置为1×108kN/m,如图7所示。
由于H型钢轨枕结构厚度远小于结构尺寸满足壳单元特征,所以采用壳单元Shell 63模拟H型钢轨枕;轨枕扣件采用纵向、横向、垂向3组Combin 14弹簧单元模拟。因为在实际工程中H型轨枕相对于承轨台只在垂向有小位移,所以纵向和横向用大刚度模拟螺栓约束,轨枕垫片垂向刚度为2×108N/m;梁体和承轨台均采用8节点实体单元Solid 185建模,模型具体参数如表3所示。
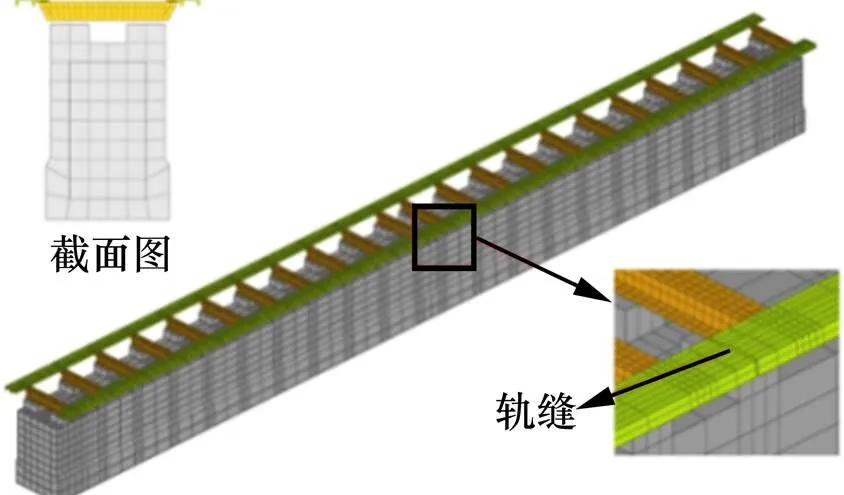
图6 轨排-桥梁有限元模型

图7 F轨轨缝连接处弹簧布置图

表3 中低速磁浮轨排与桥梁材料参数表
2.3 中低速磁浮列车-轨排-桥梁耦合动力学模型
利用有限元软件ANSYS计算轨排-桥梁耦合动力学模型,得到前20阶模态信息。将模态信息导入UM软件中得到轨排-桥梁柔性体。利用Maglev悬浮力元将新型中低速磁浮列车和轨排-桥梁耦合,建立新型中低速磁浮列车-轨排-桥梁耦合动力学模型,如图8所示。

图8 磁浮列车-轨排-桥梁耦合动力学模型
3 耦合动力学仿真分析
3.1 线路设置
为了分析研究新型中低速磁浮列车-轨排-桥梁耦合系统的动力学特性,分别计算新型中低速磁浮列车以不同的速度通过柔性轨排-桥梁结构的动力响应,暂不考虑曲线工况,路线设置为直线,并加载线路不平顺。
3.2 轨道结构几何精度误差
根据CJJ/T262—2017《中低速磁浮交通设计规范》[17]中所规定的轨道结构几何精度要求,前后高低(10 m弦矢高)的偏差值限制为±3 mm/10 m,对轨排接缝允许偏差(垂向)偏差值限制为±1 mm/1 mm。由于现有文献很少对相关几何精度要求做系统的分析,所以本文针对要求中的前后高低(10 m弦矢高)和轨排接缝允许偏差(垂向)进行研究。

图9 台阶叠加随机不平顺轨道谱
在考虑轨道接缝允许偏差(垂向)以下称台阶时,本文同时考虑了上台阶和下台阶的工况,而且还叠加上文所述的随机不平顺,台阶和随机不平顺叠加如图9所示。
3.3 悬浮力元数量研究
根据上文对悬浮力的分析,对分别取1,3和5,对应建立1个,3个和5个Maglev力元模拟一个悬浮电磁铁线圈悬浮力的新型中低速磁浮列车动力学模型。3个动力学模型中的Maglev力元数量和悬浮电磁铁常数成反比,其他参数均相同,设置磁浮列车运行速度为60 km/h,分别进行动力学计算,得到相关动力学结果。
图10(a)为列车60 km/h运行时悬浮间隙时域对比,单力元模型悬浮间隙明显大于其他2个模型,且在通过F轨轨缝时单力元模型的最大悬浮间隙分别比另外2个模型大0.85 和0.91 mm,而三力元模型和五力元模型悬浮间隙接近;图10(b)为不同速度等级下3个动力学模型的悬浮间隙最大值对比,单力元模型悬浮间隙和另外2个模型偏差较大。
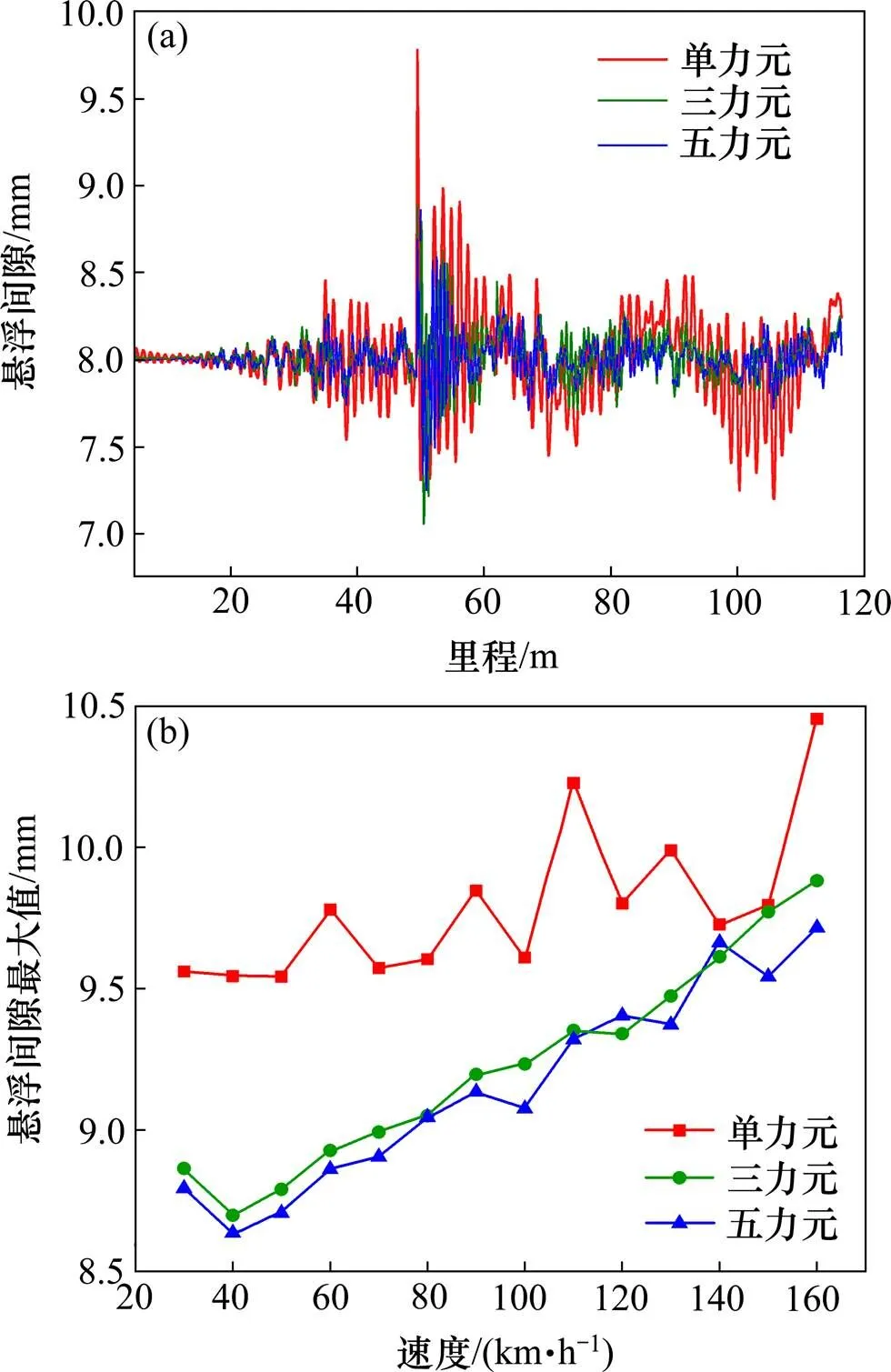
(a) 悬浮间隙;(b) 悬浮间隙最大值
图11为3个磁浮列车动力学模型以60 km/h速度通过柔性轨排-桥梁模型时悬浮架垂向加速度的时域对比,可以看出,单力元模型的悬浮架垂向加速度始终小于其他2个模型,且在通过F轨轨缝时单力元模型的悬浮架垂向加速度显著小于另外2个模型,而三力元模型的悬浮架垂向加速度和五力元模型更接近。

图11 悬浮架垂向加速度
图12为3个磁浮列车动力学模型以60 km/h速度通过柔性轨排-桥梁模型时的桥梁跨中垂向加速度的时域对比,可以看出,单力元模型的桥梁跨中垂向加速度小于其他2个模型,单力元模型的桥梁跨中垂向加速度最大值为0.19 m/s2,小于三力元、五力元模型对应的0.33 和0.30 m/s2,而三力元模型和五力元模型悬浮架垂向加速度相差较小。

图12 桥梁跨中垂向加速度
对比分析3个模型,结果表明:单力元模型在悬浮间隙和悬浮架加速度等动力学指标的计算上不够准确,同时考虑计算时间和计算精度的因素,三力元模型是合适的。
3.4 前后高低(10 m弦矢高)
分别选取偏差值为+3 mm/10 m,+5 mm/10 m,+7 mm/10 m,-3 mm/10 m,-5 mm/10 m和-7 mm/10 m作为研究变量,列车AW3工况,列车运行速度从30 km/h至160 km/h以10km /h为间隔取14个速度等级,共计84个计算工况,然后对车体平均最大垂向加速度、最大悬浮间隙、最小悬浮间隙、桥梁跨中最大加速度进行研究分析。
图13为不同轨道前后高低(10 m弦矢高)对车体平均最大垂向加速度的影响,车体平均最大加速度随着行车速度的增大而增大,在速度为50~60 km/h时车体平均最大垂向加速度突然增大,这是由于列车通过轨道梁时轨道对车辆施加周期力,周期力的频率=(m/s)/25(m),行车速度为50~60 km/h时,轨道梁周期力的频率靠近车体的垂向固有频率0.62 Hz发生共振现象。根据GB/T 5599[18]中客车运行平稳性的规定,当速度小于120 km/h所有工况的车体平均最大加速度均为优,当速度大于120 km/h时且偏差值为-7 mm/10 m,车辆运行平稳性逐渐从良好变为合格甚至在160 km/h时出现不合格。
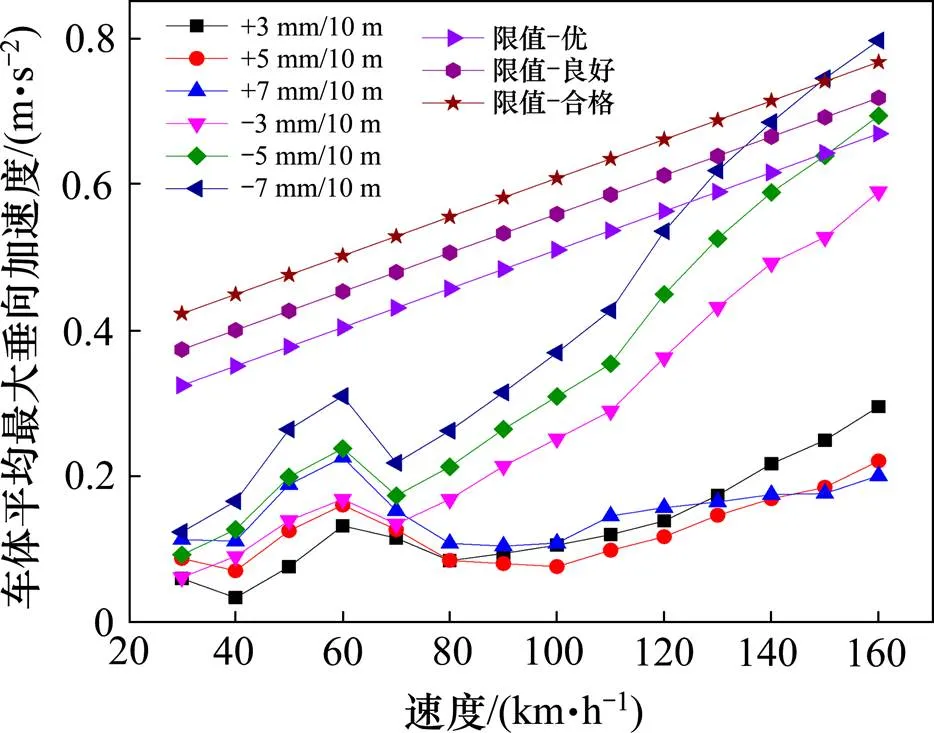
图13 Mc1车车体平均最大垂向加速度
图14为不同轨道前后高低(10 m弦矢高)偏差值时的Mc1车首悬浮架最大悬浮间隙、最小悬浮间隙,悬浮间隙最值随着行车速度的增大而越发偏离平衡位置,且悬浮间隙最值随着轨道前后高低(10 m弦矢高)偏差值的增大而增大(或减小),从数值可以看出,悬浮间隙在8±1.5 mm范围内变化。
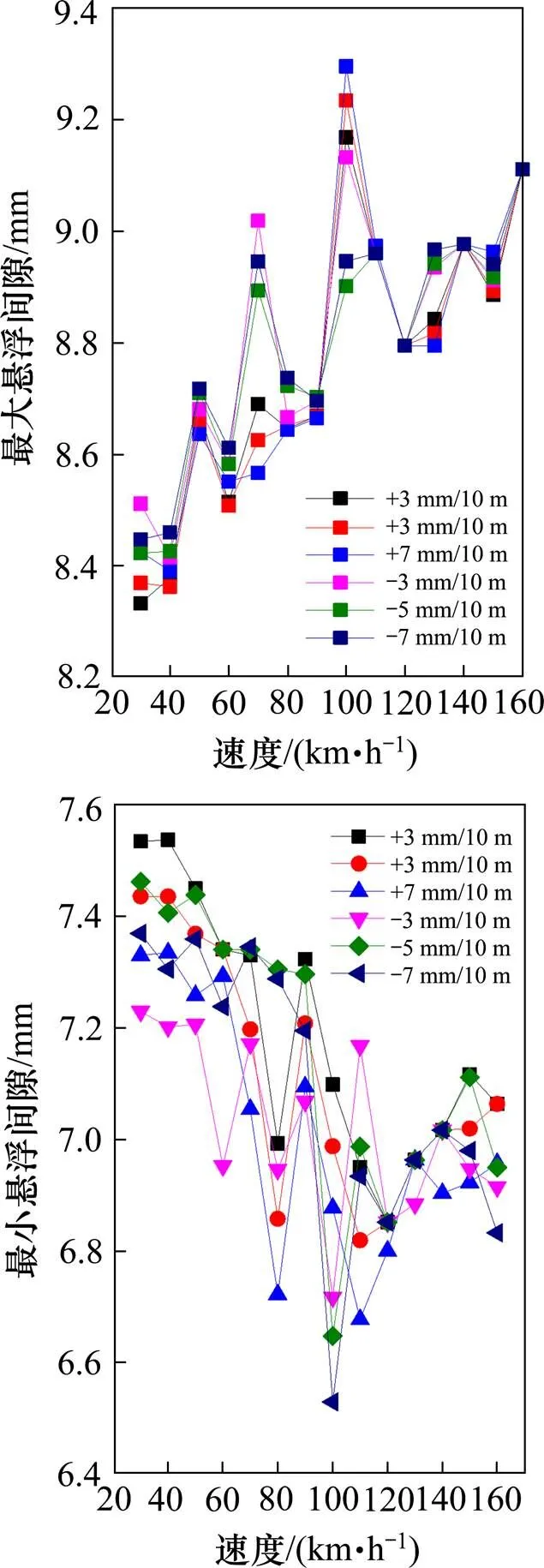
图14 Mc1车悬浮间隙
图15为不同轨道前后高低(10 m弦矢高)偏差的桥梁跨中动力系数,负偏差值对桥梁跨中动力系数的影响大于正偏差值,全部工况的动力系数范围在1.04~1.08之间,小于《中低速磁浮交通设计规范》中的规定值1.21,是偏于安全的。
图16给出了新型中低速磁浮列车在不同速度下通过不同轨道前后高低(10 m弦矢高)偏差值时的接缝处F轨最大垂向加速度,最大垂向加速度随着轨道前后高低偏差值的增大而增大,随着磁浮列车运行速度的增大而增大,所有工况中F轨最大垂向加速度最大值仅为0.66 m/s2,F轨加速度小于高速铁路无砟轨道加速度。
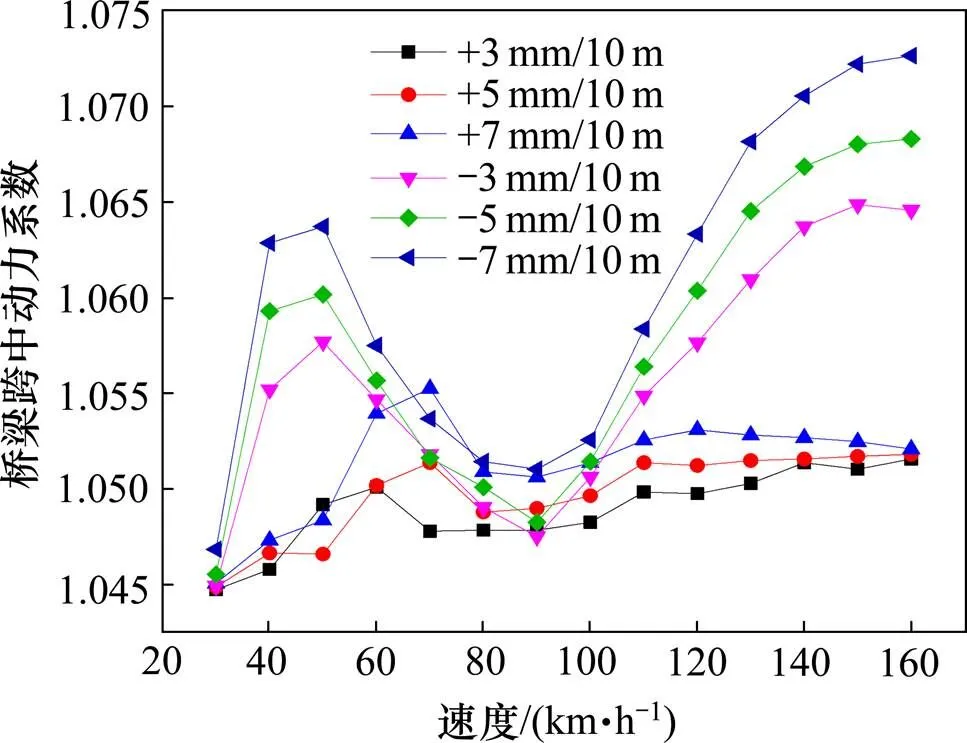
图15 桥梁跨中动力系数
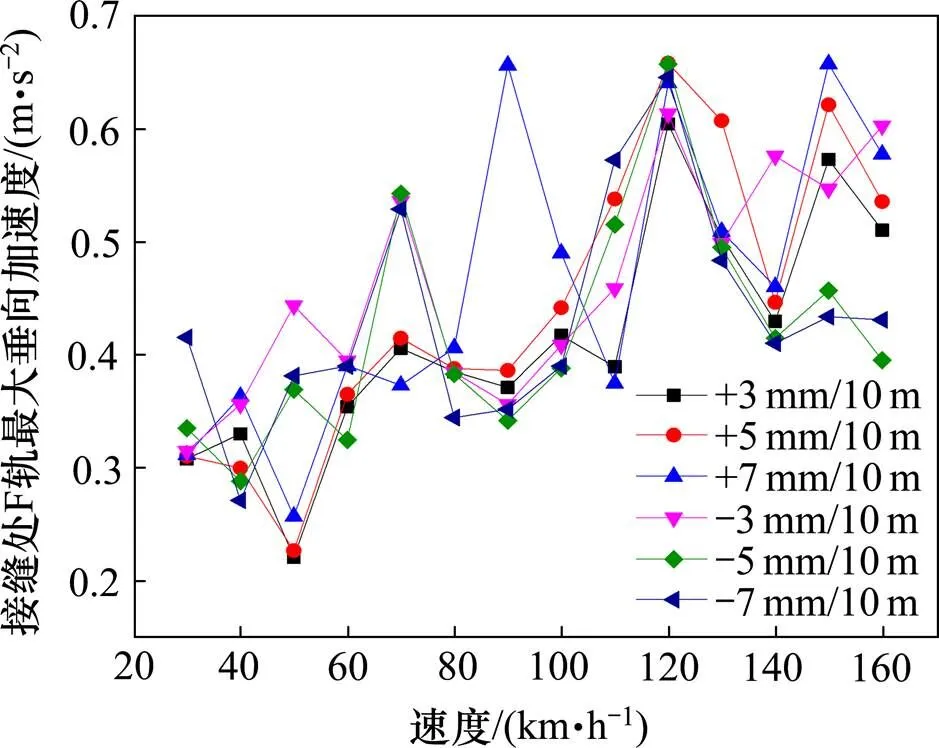
图16 接缝处F轨最大垂向加速度
3.5 轨排接缝允许偏差(垂向)
分别选取+1,+2,+3,-1,-2和-3 mm台阶作为研究变量,列车AW3工况,列车运行速度从30 km/h至160 km/h,对车体平均最大垂向加速度、最大悬浮间隙、最小悬浮间隙、桥梁跨中最大加速度进行研究分析。
图17为不同台阶偏差值时Mc1车车体平均最大垂向加速度,车体平均最大加速度随着行车速度的增大而增大;根据GB/T 5599中客车运行平稳性的规定,所有工况的运行平稳性均为优。这是由于车体振动为低频振动,频率一般在5 Hz以下,磁浮列车通过台阶时产生的是高频冲击振动,由于空气弹簧的滤波作用悬浮架的高频振动不会传递到车体上,所以台阶对车体平均最大垂向加速度影响很小。
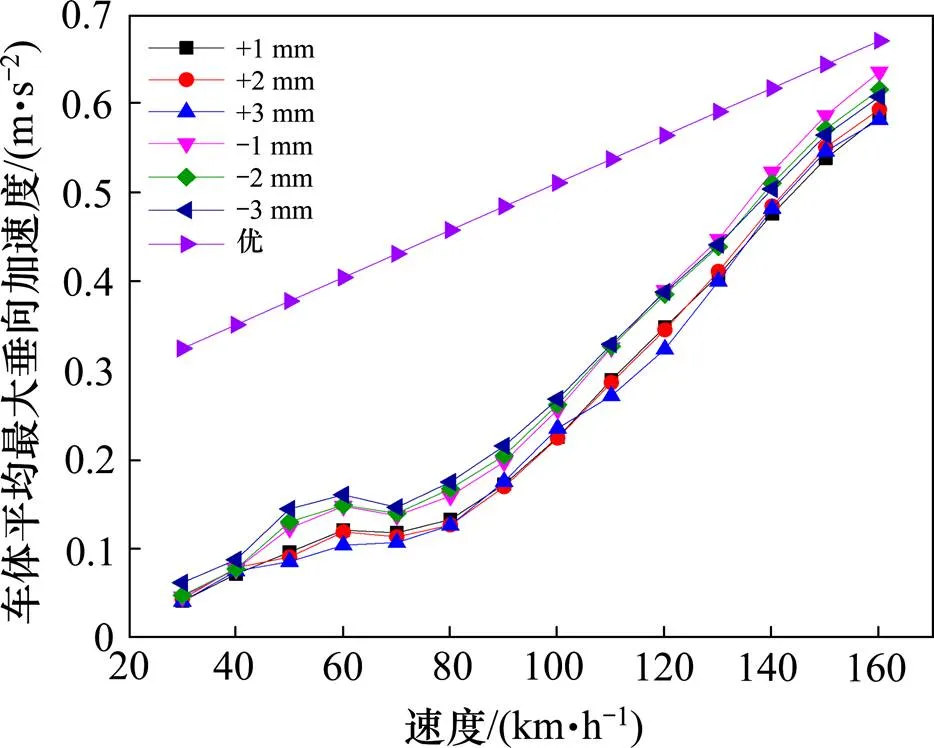
图17 Mc1车车体平均最大加速度
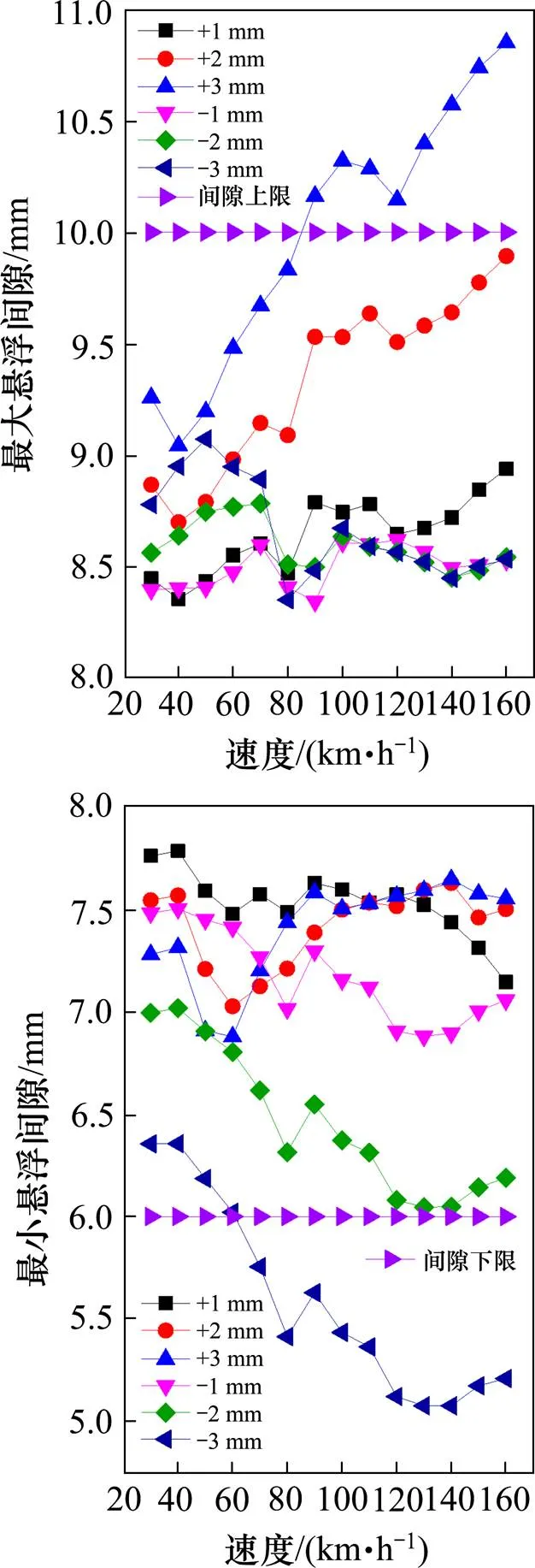
图18 Mc1车悬浮间隙
图18为不同台阶偏差值时的Mc1车首悬浮架悬浮间隙,正台阶偏差值时的最大悬浮间隙随着行车速度的增大而增大,正台阶主要影响最大悬浮间隙的变化,负台阶偏差值工况下的最小悬浮间隙随着行车速度的增大而减小,负台阶主要影响最小悬浮间隙的变化。+3 mm台阶工况下,当列车运行速度大于80 km/h时最大悬浮间隙超过悬浮间隙上限值。-3 mm台阶工况下,当列车运行速度大于50 km/h时最小悬浮间隙超过悬浮间隙下限值。
图19为不同轨道接缝允许偏差(垂向)偏差值时的桥梁跨中动力系数,正偏差值对桥梁跨中动力系数的影响大于负偏差值,全部工况的动力系数范围在1.05~1.08之间,小于《中低速磁浮交通设计规范》中的规定值1.21,是偏于安全的。
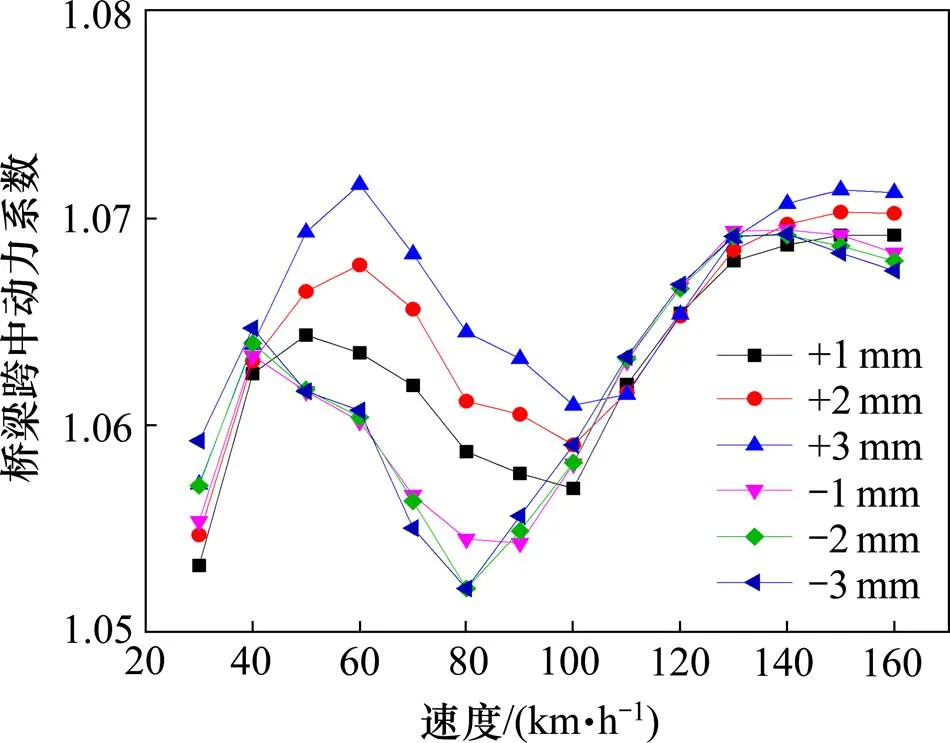
图19 桥梁跨中动力系数
图20给出了新型中低速磁浮列车在不同速度下通过不同台阶偏差值时的接缝处F轨最大垂向加速度,最大垂向加速度随着台阶偏差值的增大而增大,但是在某些速度发生共振现象,加速度幅值增加,这是由于车辆会对轨排-桥梁结构产生周期力,周期力的频率=(m/s)/(m),其中为车辆特征 长度。
图21为速度共振图,当列车运行速度在60 km/h左右时,以悬浮架长度为特征长度产生周期力的频率与轨排-桥梁结构一阶垂弯接近,所以引起共振,此时轨缝处F轨最大垂向加速度陡增,所有工况中F轨最大垂向加速度最大值为1.04 m/s2。
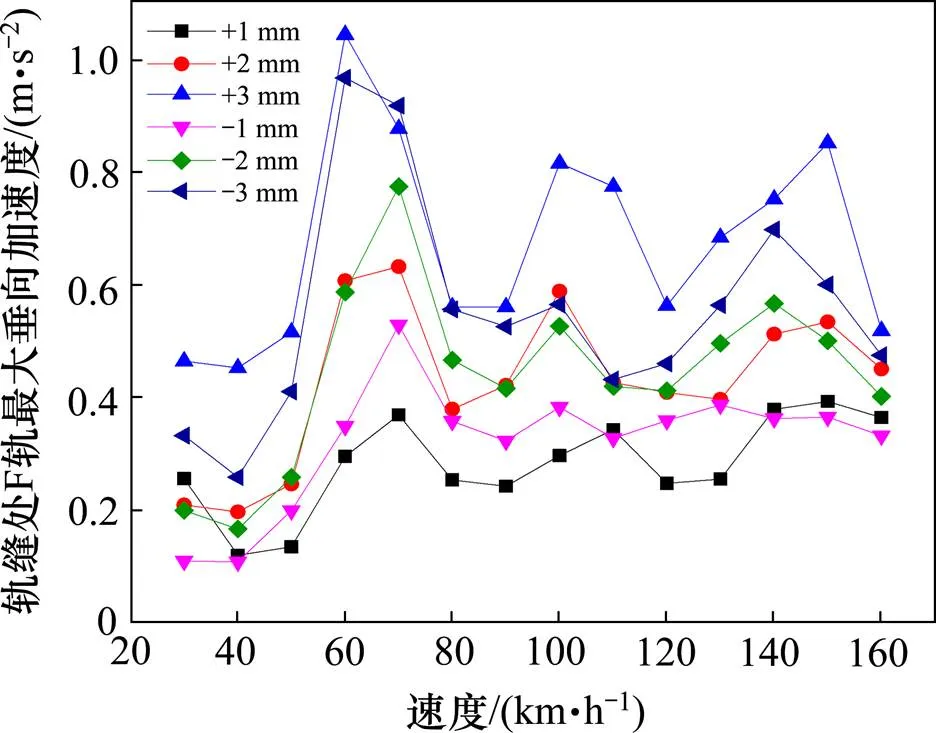
图20 轨缝处F轨最大垂向加速度
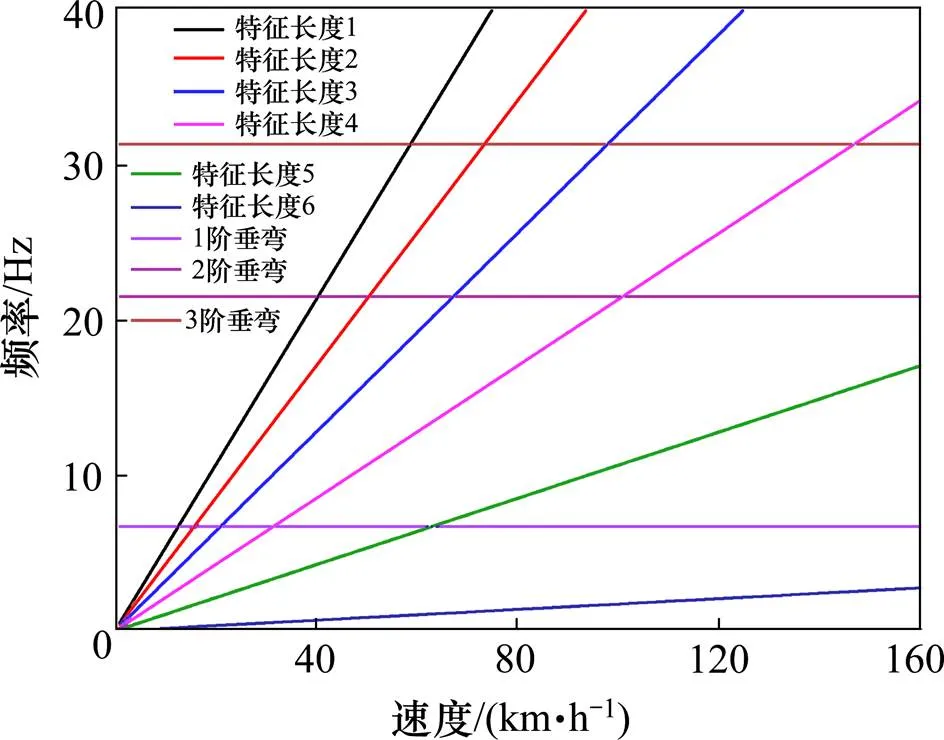
图21 速度共振图
4 结论
1) 悬浮电磁力和间隙磁通密度的平方成正比的关系,气隙磁密在悬浮电磁铁长度上基本平均分布,证明了用个简化力元模拟悬浮力在工程实际中是可行的,对比3个动力学模型仿真计算结果,表明使用三力元动力学模型合适。
2) 不同轨道前后高低(10 m弦矢高)对运行平稳性指标影响较为明显,若想保持运行平稳性为优,在实际工程中应该严格控制负偏差,轨道前后高低(10 m弦矢高)偏差值应不大于+7 mm/10 m,不小于-5 mm/10 m。
3) 不同轨排接缝允许偏差(垂向)对悬浮间隙最值影响较大,对运行平稳性、桥梁跨中动力系数影响较小,接缝处F轨最大垂向加速度随台阶增大而增大,但是和轮轨交通相比其值均较小。由于新型中低速磁浮列车悬浮架动力作用更低,所以台阶允许偏差可以控制在2 mm以内。
[1] Lee H, Kim K, Lee J. Review of maglev train technologies[J]. IEEE Transactions on Magnetics, 2006, 42(7): 1917-1925.
[2] 赵春发. 磁悬浮车辆系统动力学研究[D]. 成都: 西南交通大学, 2002. ZHAO Chunfa. Maglev vehicle system dynamics[D]. Chengdu: Southwest Jiaotong University, 2002.
[3] YAN L G. Development and application of the maglev transportation system[J]. IEEE Transactions on Applied Superconductivity, 2008, 18(2): 92-99.
[4] ZHANG M, LUO S, GAO C, et al. Research on the mechanism of a newly developed levitation frame with mid-set air spring[J]. Vehicle System Dynamics, 2018, 56(12): 1797-1816.
[5] REN S, Rmeijn A, Klap K. Dynamic simulation of the maglev vehicle/guideway system[J]. Journal of Bridge Engineering, 2010, 15(3): 269-278.
[6] YAU J D. Response of a maglev vehicle moving on a series of guideways with differential settlement[J]. Journal of Sound and Vibration, 2009, 324(3-5): 816- 831.
[7] CAI Y, CHEN S S, Rote D M, et al. Vehicle/guideway interaction for high speed vehicles on a flexible guideway[J]. Journal of Sound and Vibration, 1994, 175(5): 625-646.
[8] CAI Y, CHEN S S. Dynamic characteristics of magnetically-levitated vehicle systems[J]. Applied Mechanics Reviews, 1997, 50(11): 647-670.
[9] 曾佑文, 王少华, 张昆仑. EMS磁浮列车-轨道垂向耦合动力学研究[J]. 铁道学报, 1999(2): 30-34. ZENG Youwen, WANG Shaohua, ZHANG Kunlun. A study of vertical coupling dynamics of EMS maglev train and guideway systems[J]. Journal of the China Railway Society, 1999(2): 30-34.
[10] SHI J, WEI Q, ZHAO Y. Analysis of dynamic response of the high-speed EMS maglev vehicle/guideway coupling system with random irregularity[J]. Vehicle System Dynamics, 2007, 45(12): 1077-1095.
[11] 梁鑫, 罗世辉, 马卫华, 等. 磁浮列车单铁悬浮车桥耦合振动分析[J]. 交通运输工程学报, 2012, 12(2): 32-37. LIANG Xin, LUO Shihui, MA Weihua, et al. Coupling vibration analysis of single-magnet suspension vehicle- bridge for maglev train[J]. Journal of Traffic and Transportation Engineering, 2012, 12(2): 32-37.
[12] Kim K J, HAN J B, HAN H S, et al. Coupled vibration analysis of maglev vehicle-guide way while standing still or moving at low speeds[J]. Vehichle System Dynamics, 2015, 53(4): 587-601.
[13] 汪科任, 罗世辉, 宗凌潇, 等. 新型磁浮车动力学仿真分析[J]. 振动与冲击, 2017, 36(20): 23-29. WANG Keren, LUO Shihui, ZONG Lingxiao, et al. A dynamic simulation analysis of new maglev trains[J]. Journal of Vibration and Shock, 2017, 36(20): 23-29.
[14] 任晓博. 中低速磁浮车辆-轨道-桥梁耦合振动仿真分析[D]. 成都: 西南交通大学, 2018. REN Xiaobo. Numerical analysis on coupled vibration of medium-low speed maglev vehicle-track-viaduct system [D]. Chengdu: Southwest Jiaotong University, 2018.
[15] 魏高恒, 陈晓昊, 罗世辉, 等. 轨道高低不平顺对磁浮车辆动力学性能的影响[J]. 机车电传动, 2019(4): 56-60. WEI Gaoheng, CHEN Xiaohao, LUO Shihui, et al. Influence of track vertical irregularity on dynamic performance of maglev vehicles[J]. Electric Drive for Locomotives, 2019(4): 56-60.
[16] 全顺喜. 中低速磁浮轨道伸缩接头的布置及结构设计[J]. 铁道工程学报, 2017, 34(8): 62-66. QUAN Shunxi. Arrangement and design of expansion rail joints in medium-low-speed maglev transit[J]. Journal of Railway Engineering Society, 2017, 34(8): 62-66.
[17] CJJ/T262—2017, 中低速磁浮交通设计规范[S]. CJJ/T262—2017, Code for design of medium and low speed maglev transit[S].
[18] GB/T 5599—1985, 铁道车辆动力学性能评定和试验鉴定规范[S]. GB/T 5599—1985, Railway vehicles specification for evaluation the dynamics performance evaluation and testing[S].
Influence of geometry accuracy of track structure on dynamic performance of the coupled medium-low speed maglev train-rail-bridge system
AO Jianan1, WEI Gaoheng2, MA Weihua3, ZHOU Ce3, LUO Shihui3, YU Yao4
(1. CRCC Dalian Locomotive & Rolling Stock Co., Ltd., Dalian 116022, China;2. China Railway Siyuan Survey and Design Group Co., Ltd., Wuhan 430063, China;3. Traction Power State Key Laboratory, Southwest Jiaotong University, Chengdu 610031, China;4. Key Laboratory of Traffic Safety on Track, Ministry of Education, Central South University, Changsha 410075, China)
In order to address the shortcoming of using few numbers of concentrated forces to simulate the electromagnetic levitational forces in previous studies. The theoretical calculation formula and finite element calculation results of levitational forces were introduced. The modeling method of levitational forces was studied. A tourism maglev transit line with the new type of medium-low speed maglev train and 25 m simply supported bridge beams was taken as a case study. The dynamic model of the coupled medium-low-speed maglev train-rail-bridge system was established. The dynamic calculation results of maglev train with different numbers of maglev force elements were compared. The influences of the longitudinal level of rail beams (10 m chord vector height) and the allowable deviation of the rail joints (vertical) on the dynamic characteristics of the system were studied. The results show that it is feasible in engineering practice to simulate the levitational forces with several levitational force elements, and that the three-force element model has a faster calculation speed and higher accuracy. The allowable deviation of the rail joint (vertical) has a greater impact on the levitation gap and the maximum vertical acceleration of the levitational bogies. The allowable deviation of the rail joint (vertical) should be controlled within ±2 mm.
new medium-low speed maglev; levitational force; track geometry; panel of rails; beam; dynamic simulation
U266.4;U441.7
A
1672 - 7029(2020)11 -2738 - 10
10.19713/j.cnki.43-1423/u.T20200511
2020-06-08
国家自然科学基金资助项目(51875483)
马卫华(1979-),男,山东滕州人,研究员,博士,从事机车及重载列车动力学、磁浮列车悬浮架设计及常导列车动力学研究;E-mail:mwh@swjtu.edu.cn

(编辑 蒋学东)
