例谈求解条件概率的两种基本策略

广东省惠州市第一中学 (516007) 方志平

由于条件概率相对一般概率概念更为抽象，涉及的事件关系更为复杂，相关概念也极易混淆,所以条件概率是高中数学教学的一个难点，基于此本文举例剖析，以期帮助同学们走出有关条件概率的解题困境.

1.直接利用条件概率公式求解

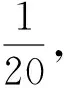
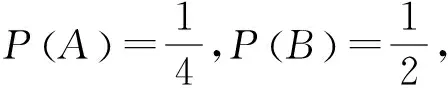
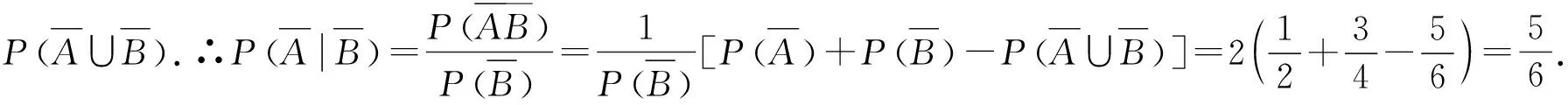
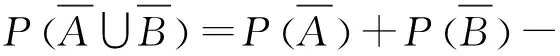
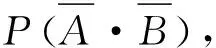
例3 设某公路上行驶的货车和客车的比例为2:1, 货车在中途停车修车的概率为0.02, 客车在中途停车修车的概率为0.01, 今有一辆汽车停车修理, 求该汽车是货车的概率.

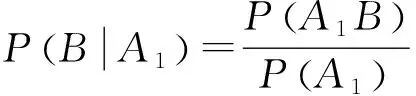
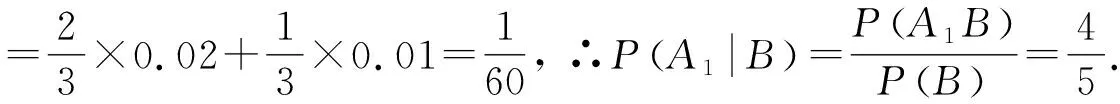
评注：本题关键要理解“今有一辆汽车停车修理”是前提条件，在此条件下求这辆汽车是货车的概率.

例4 某医院用一仪器对某种疾病进行初步诊断, 已知这种仪器对患病者的正确诊断概率有0.9；对没患病者的正确诊断率有0.8.已知这种疾病在人群中的患病的比例为0.1, 若某人去医院就诊, 在医院通过这种仪器初诊给出的诊断结论是已患病的条件下, 求此人真正患这种病的概率.

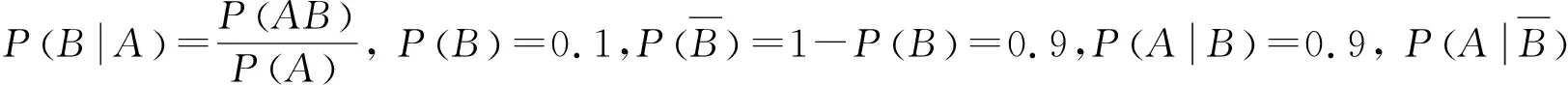
评注：本题用到的公式比较多，关键是要理解条件概率的定义，分清谁是条件，谁是结论，灵活运用条件概率计算公式及其变形形式.

2.缩减样本空间利用古典概型求解

例5 将三颗骰子各掷一次，记事件A=“三个点数都不同”，B=“至少出现一个6点”，则条件概率P(B|A),P(A|B)分别等于( ).

解：事件AB：“当且仅当三颗骰子中点数都不同且只出现一个6点”.

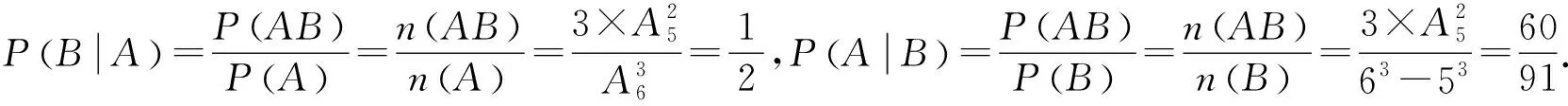
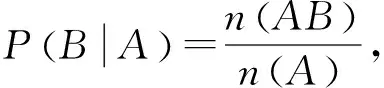
例6 某校篮球队假期集训，集训前共有6个篮球，其中3个是新球(即没有用过的球)，3 个是旧球(即至少用过一次的球)．每次训练，都从中任意取出2个球，用完后放回．求第二次训练时恰好取到一个新球的概率.

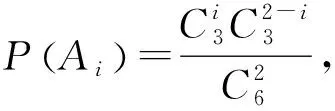
评注：本题要注意一个常识，即新球训练过后就变成了旧球，所以要计算第二次恰好取到一个新球的概率，需要了解经过第一次训练后，所剩的球有几个新球，几个旧球，所以要对第一次取球的情况进行分类讨论，然后分别计算概率再相加即可.

例7 设盒中有10个球，其中红球4个，白球6个，今从中不放回地接连取出4个球，已知至少取出一个红球，求至少取出两个红球的概率.

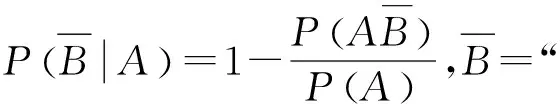
评注：题中已假设“至少取出一个红球”为事件A，在这一条件下，事件B：“至少取出两个红球”的情形较为复杂，因此考查其对立事件的概率可找到问题解决的突破口.

综上，解决条件概率问题，除此之外，还有其它的求解策略，本文只是探讨了求解条件概率问题的冰山一角，仅供读者参考.这里特别强调，求解条件概率问题，首先要充分理解事件(B|A)中条件“A”的必然性和事件“B”的随机性.事件AB与(B|A)的落脚点不同，前者是指在原概率空间中的两个事件同时发生，关键词是“原概率空间”、“同时”，后者指缩减概率空间后，事件“B”发生的概率，强调的是“B”，而非“A”、“B”“同时”，也不是“A”先发生“B”后发生，关键点“A”是已经“发生过了”的必然事件，在此基础上，事件“B”又发生了.