莫让浮云遮望眼，撩开雾纱见真颜——2020年高考全国卷Ⅰ第20题探究

福建省龙岩市永定区教师进修学校 (364100) 黄初灿

1.试题再现

(1)求E的方程；(2)证明：直线CD过定点.

该题集基础性、综合性、创新性于一体，解法多样，每一种解法各有千秋，给不同层次考生不同选择，区分度好，具有选拔性.考查了椭圆的方程，椭圆的几何知识，向量的数量积，直线与椭圆的位置关系等基础知识，考查运算求解能力，考查数形结合思想，化归与转化思想等，涉及的核心素养有逻辑推理、数学运算、直观想象等.

2.解法赏析

评析：在标答中有2个地方比较抽象，学生认为是天马行空，神来之笔，特地有咨询过笔者，就是如何得到①式和②式.如何得到①式，其实只要把x1=my1+n，x2=my2+n分别代入27y1y2=-(x1+3)(x2+3)化简就可以得出①式.又因为(27+m2)(n2-9)-2m(n+3)mn+(n+3)2(m2+9)=0，所以(n+3)[(27+m2)(n-3)-2m2n+(n+3)(m2+9)]=0，所以(n+3)(36n-54)=0，从而得出②式.增加这样解释后是不是更好点.

评析：该解法思路清晰，通俗易懂，学生更容易接受.难点在于直线CD的斜率的化简，及直线CD方程的化简.

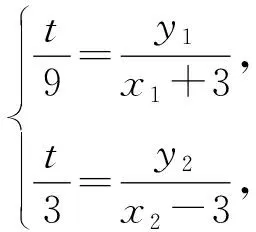
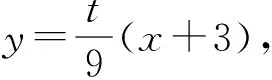
3.试题探源

很明显，2020年全国卷Ⅰ第20题源于此题的第(3)问.

4.结论探究

该题中，我们自然会问，“P为直线x=6上的动点”改为“P为直线x=t上的动点”，那么直线CD还会过定点吗？经过探究，有以下结论：

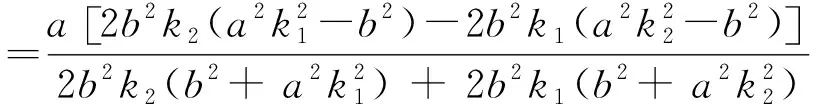
对于双曲线和抛物线也有类似结论：

同理对抛物线有：

结论3 已知抛物线E：y2=2px(p>0)的顶点为O，点P在直线x=t上，直线PO交E于另外一点C，过点P且平行于x轴的直线交E于点D，则直线CD必过定点(-t,0).

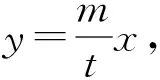
上述几个命题的逆命题也会成立.限于篇幅，读者可再作探究.

5.教学反思

圆锥曲线定值、定点问题是高考的热点，今年全国卷I、新全国卷(山东卷)都考查到定值、定点问题.在解析几何教学中，要关注利用代数手段研究几何问题，对于高频率考点(弦长、三角形面积、定值定点等知识)要做到分析试题的变式、内涵及来源，并引导学生归纳、总结、优化解题方法.