一个三元分式不等式的下确界

广东省中山纪念中学 (528454) 邓启龙

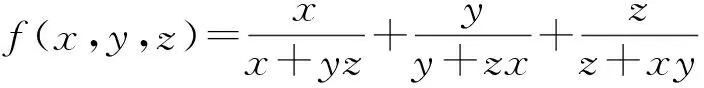
文[1]确定了f(x,y,z)的上确界,本文得到了f(x,y,z)的下确界.

(1)当0<λ≤1时,f(x,y,z)的下确界为2,当x→0+,y→y0,z→z0(y0,z0>0且y0+z0=λ)时,f(x,y,z)→2.

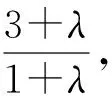
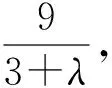
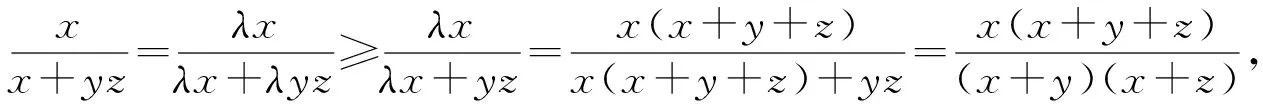
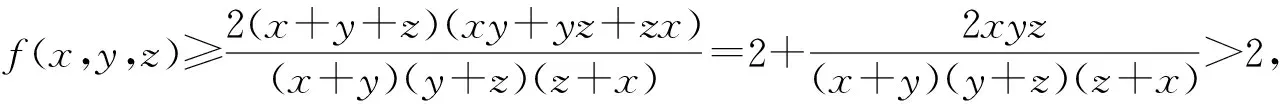
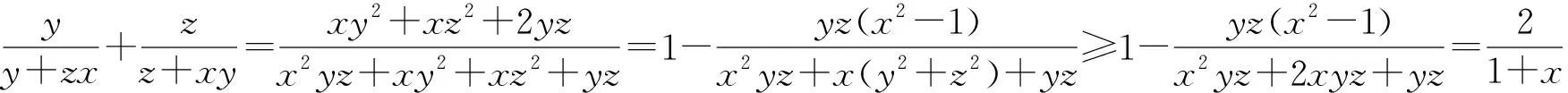
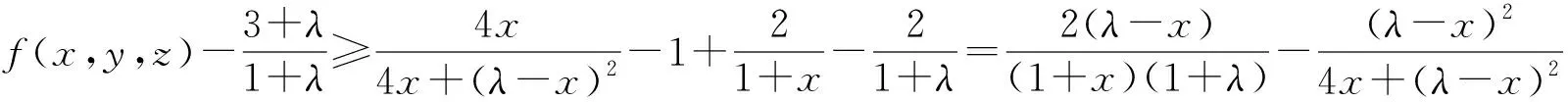
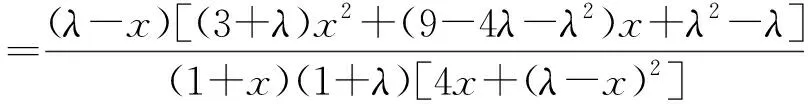
当1<λ<3且max{x,y,z}<1时,f(x,y,z)的下确界有待进一步研究.最后,本文提出以下猜想:

当1<λ<3且max{x,y,z}≥1时,本文已解决f(x,y,z)的下确界.所以猜想1等价于证明以下问题: