探求错误根源，追寻问题本质*——从哲学角度看学生的数学错解

广东省中山市第一中学 (528400) 李 虎

数学课程中，可以嫁接人文学科的一些知识背景，来渗透善和美，笔者认为可以立足本学科，挖掘更深层次数学课程中蕴含的善美元素，为学生的全面发展打好基础.本文笔者从几个不同的角度加以阐述.

一、重视概念教学，建立正确的逻辑起点

A.充分不必要条件 B.必要不充分条件

C.充要条件 D.既不充分也不必要条件

分析：错误认为曲线上经过某点的切线有且只有一条，发现在此点的切线满足题意，就认为是充要条件了.

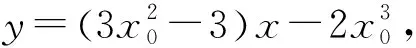
类题演练1：已知函数f(x)=2x3-3x，若过点P(1,t)存在3条直线与曲线y=f(x)相切，求t的取值范围.

点评：本题是根据切线与导数的关系将切线条数问题的等价转化为函数零点个数问题.部分同学是对充分必要条件理解不清，部分同学概念理解不到位，概念模糊不清直接导致了一系列的错误.这给教学的启示是第一遍教学时，课堂一定要舍得花时间去把概念落实到位.现在复习阶段，遇到这个问题怎么处理呢？对于基础薄弱的学生，笔者建议可以画概念图，同时辅助习题训练将知识体系完备起来.

二、细节把握的度，宏观微观并重

例2 已知函数f(x)=ln(ax)-ax2+x(a≠0).讨论函数f(x)的单调性.

分析：本题讨论函数的单调性，需要注意定义域随着参数a的正负在改变，若忽视定义域极易出现错误；此外本题需要讨论二次函数根的分布，两根的大小比较也是一个容易出错的地方.

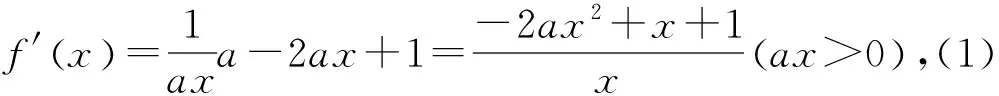
类题演练2：关于圆周率π，数学发展史上出现过许多有创意的求法，如著名的普丰实验和查理斯实验．受其启发，我们也可以通过设计下面的实验来估计π的值：先请120名同学每人随机写下一个x,y都小于1的正实数对(x,y)，再统计其中x,y能与1构成钝角三角形三边的数对(x,y)的个数m，最后根据统计个数m估计π的值．如果统计结果是m=34，那么可以估计π的值为( ).

点评：导数多年来一直在压轴题的位置.高三教学复习，既要注意宏观上的大局，同时要注意细节.目前核心素养的考查，打破了原来固有的命题模式，那么如何把握大局？要深刻理解核心素养，深刻理解课程准，要把学生的能力真正培养起来.

三、抓主要矛盾和矛盾的主要方面

分析：该问题处理的第一步的换元，然后是分离参数.对于分离后函数的研究又是一个难点，并且涉及到了极限.

图1

四、结语

数学在人类的发展进程中起着重要的作用，数学作为很多学科的基础，有着其独特的育人价值.数学的德育价值，高中阶段研究较少，但其又有很好的研究价值.数学中隐性德育的挖掘，是数学老师应该思考的一个重要问题，但数学课程毕竟是数学课程，不能将其变成德育课程.隐性德育的魅力也在这里，蕴含其中而又不外显，在潜移默化中优化学生的思维品质和人格.