堰塞湖土料冲蚀特性测量系统研究
2020-12-14李炎隆武钰淼
王 琳,李炎隆,武钰淼
(西安理工大学 西北旱区生态水利国家重点实验室, 陕西 西安 710048)
堰塞湖是一种典型的地质灾害,具有坝体结构松散、几何形态各异、溃决风险高、溃决致灾后果严重等特点。近年来,我国堰塞湖呈现大规模、高频率、群发性、风险持续增加的趋势,是目前堰塞湖溃决数量最多的国家[1]。堰塞湖一旦溃决,极易形成灾害链,威胁下游人民群众的生命财产安全[2]。
据统计[3],9%的堰塞湖在1小时内溃决,34%在1天内溃决,67%在1个月内溃决。2000年4月,易贡堰塞湖[4]形成,溃决时峰值流量达到94 810 m3/s。2008年汶川特大地震造成257处堰塞湖,其中最具代表性的是唐家山堰塞湖[5]和小岗剑堰塞湖[6],溃决洪峰分别达到6 500 m3/s和3 950 m3/s,使得近百万人的生命财产安全受到威胁。2018年白格堰塞湖更是两次堵塞金沙江上游干流[7],溃决洪峰流量分别达到10 000 m3/s和31 000 m3/s[8-9],导致下游在建的苏洼龙水电站围堰拆除,叶巴滩、拉哇、巴塘等在建水电站工程延期。
冲蚀是堰塞湖溃决的主要因素之一,定量分析冲蚀过程是揭示堰塞湖坝体土料冲蚀特性的重要挑战[2]。土料的冲蚀特性以冲蚀流速(冲蚀临界剪应力)和冲蚀率表征。水流对土体表面颗粒施加剪应力,当该剪应力超过临界值时,土料发生冲蚀,对应的水流平均速度为冲蚀流速。冲蚀流速决定了土体冲蚀开始和终止的时间,是影响冲蚀率的重要参数。由于冲蚀率与剪应力的关系均呈现不同形式,进而导致溃决洪水分析计算结果极为不稳定,有时甚至不收敛。以唐家山堰塞湖为例,作者分别选用Einstein-Brown、Englund-Hensen、Du Boys和Meyer Peter & Muller四种不同的冲蚀模型开展溃决洪水分析,通过与实测数据对比[10],发现不同冲蚀模型计算出的溃决流量结果差距可达2~3倍。
因此,许多不同的冲蚀特性测量系统被开发用以研究冲蚀特性。广泛应用的有原位流槽法[11]、室内水槽法[12]、旋转圆柱测试(Rotation Cylinder Test)[13]、冲蚀装置(Erosion Function Apparatus,EFA)[14]、孔洞冲蚀测试(Hole Erosion Test)[15]、喷射冲蚀测试(Jet Erosion Test)[16]等。Wahl[17]在对HET和JET设备开展冲蚀试验对比时发现,JET设备的冲蚀率比HET高一个数量级,临界剪应力却低两个或多个数量级。可见采用不同测量系统可得到不同的冲蚀模型,由于采用的系统不同,会产生较大差异。这些冲蚀测量系统没有标准,无法模拟实际溃决洪水流速,较难测量含有大体积岩石碎块的堰塞湖土料冲蚀特性。
为模拟堰塞湖溃决过程,本文拟提出一种新的土料冲蚀特性测量方法,并通过自行研制的圆筒型冲蚀试验设备(CETA)测量土料冲蚀特性。与上述测量系统相比,自行开发的CETA具有以下优点。首先,能提供7 m/s的最高流速,可满足溃决的快速变化过程。其次,可对粗料(砂、砾石)进行试验。第三,可针对最大粒径10 cm的土料开展冲蚀试验。本文将通过介绍圆筒型冲蚀试验设备,并选用易贡堰塞湖土料开展不同粒径的启动流速和冲蚀率的试验研究,建立土体冲蚀流速与冲蚀率之间的关系式,检测土料冲蚀特性测量方法的可靠性;并通过确定剪应力计算公式,建立堰塞湖土料冲蚀率与冲蚀剪应力间的冲蚀模型。
1 圆筒型冲蚀试验设备(CETA)结构与原理
1.1 结 构
CETA由结构系统、传动系统、冲蚀试验系统、清淤循环系统和控制及数据采集系统组成,见图1。传动系统包括电机和叶轮(见图2、3)。在实验中,电机旋转并驱动叶轮,叶轮又驱动圆筒中的水流来冲刷土料样品。调速电机额定电压为220 V,最高转速为1 400 r/min,由沉砂池、水泵和散水器组成的清淤循环系统可实现水循环。土颗粒被冲走后,随水流入沉砂池,沉砂池中的水通过水泵和散水器回到筒中,而土颗粒留在沉砂池中。在圆筒的四周专门设置了3个由有机玻璃制成的观察窗,可用于观察和拍摄土体冲蚀过程,每个观察窗的尺寸约为40 cm×28 cm。另外,考虑到圆筒涡流可能会影响冲蚀过程,所以在筒底部加装了一个圆柱体的灯环,使筒底接近一个环形水槽,降低涡流的影响,提高试验的观测和拍摄效果。试样可采用原状土或重塑土,也可以是细粒土或粗粒土。此圆筒的内径为104 cm,围绕中轴的照明灯环直径为35.4 cm,灯环的高度为30 cm。
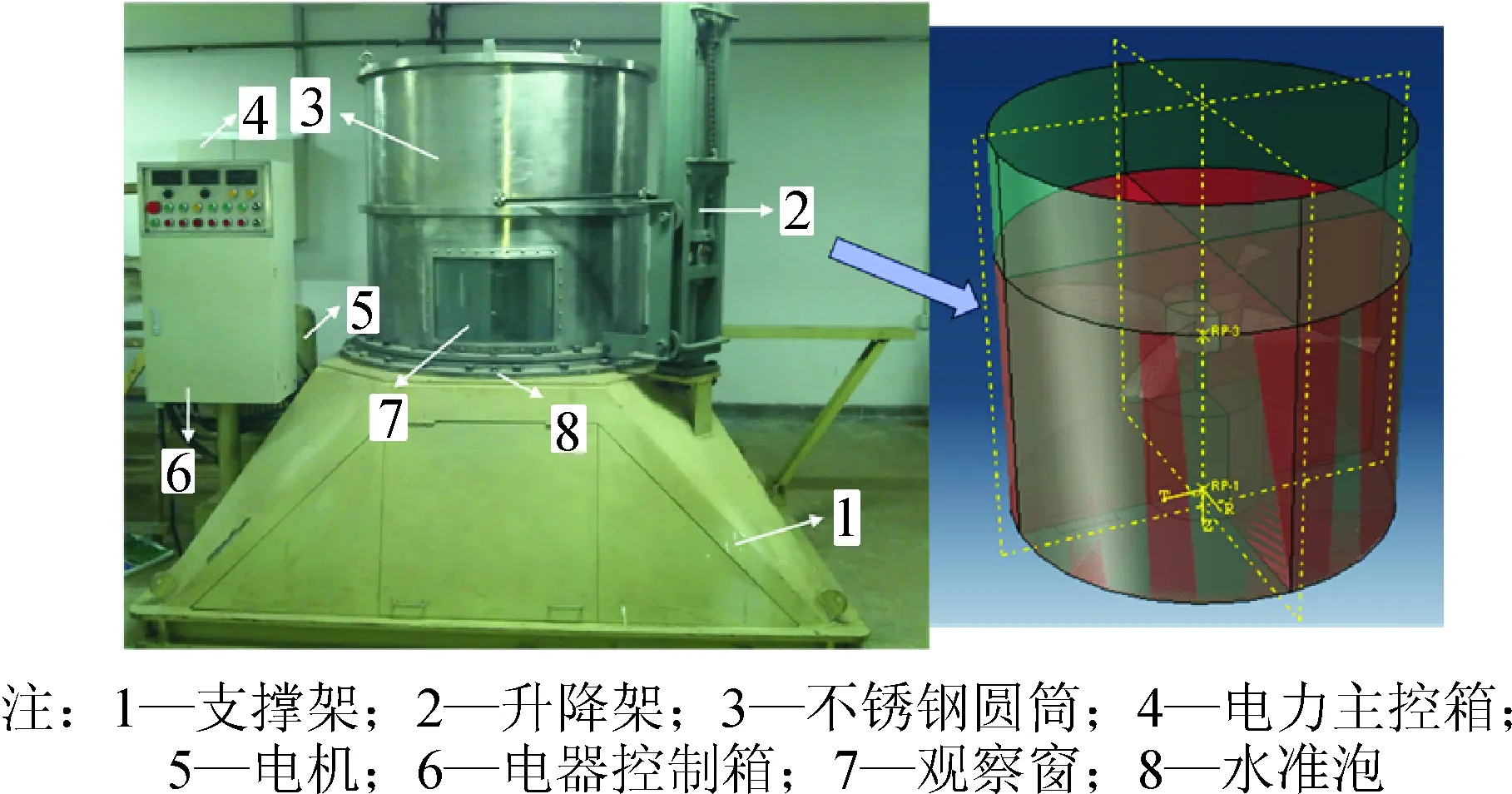
图1 圆筒型冲蚀试验设备Fig.1 Cylindrical rotating erosion apparatus

图2 电机Fig.2 Motor
1.2 原 理
设备通过电机带动叶轮转动,叶轮转动促使水流发生流动,水流启动后即冲刷已放置在圆筒底部的试样,一旦试样出现运动,此时的速度即为冲蚀启动流速。采集系统可记录流速和试样冲刷过程。设备的叶轮最大设计转速为11 m/s,试验水深范围为0.4~0.7 m。细粒料样品,如粘土、粉土和细砂,可放入土壤样品箱(见图4(a)),类似于EFA。在试验过程中,用提升系统将试样推进5 mm,记录在一定水流速度下5 mm试样的冲蚀时间,可用于模拟真实堰塞湖坝体中的粗砾料土样(见图4(b))。确定流速下的冲蚀率可通过计算固定时间内的土体冲蚀量计算。

图4 土样的两种不同布置方式Fig.4 Two different layout patterns of the soil sample
具体试验程序可简化为如下。
1) 土样制备。根据要求的密度和含水量制备土样,将制备好的土样放置在可升降的样品箱或圆筒底部。
2) 组装圆筒和摄像头。随后,将水注入圆筒,高度为55 cm。
3) 打开相机并调整其位置。
4) 打开主电源,启动设备进行预热。
5) 在冲蚀开始之前,旋转速度一直增加,并记录转速。
6) 通过采集系统测量并记录冲蚀流速和冲蚀速率。冲蚀率可由冲刷高度(5 mm)或测定时间间隔内的残余土料换算而成。
7) 根据试验要求,提高转速并重复步骤6。
8) 测试结束后,关闭电源并清洁仪器。
2 冲蚀剪应力计算方法
2.1 叶轮转速与水流速度关系的标定
圆筒型冲蚀试验设备工作时,是电机带动叶轮转动,再通过水的介质作用,将速度传递到底部的试样上。通过水的传递作用,叶轮中心位置处的流速值与底部试样位置上的流速值存在差异,需要率定。考虑到圆筒设备是新装置以及它的特殊性,选用流速仪对试验设备进行率定。采用FP111型直读式流速仪(见图5),通过测量冲蚀设备过水断面的不同位置在不同叶轮转速下的流速来对设备内部的流场进行率定,建立不同叶轮转速下设备内部流速场的分布特征,确定实测流速与叶轮转速的相关关系,图6为流速测定的测点位置示意图。

图5 FP111直读式流速仪Fig.5 FP111 reading type current meter
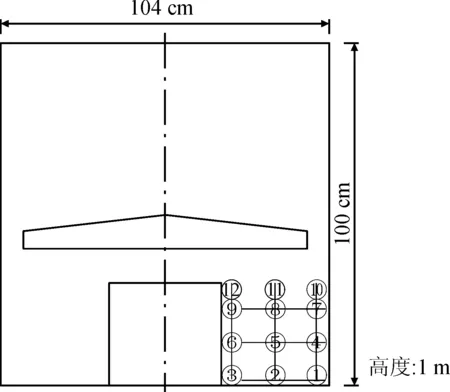
图6 测点分布图 Fig.6 Measuring point
在不一样的测点保持共同的转速,在每个测点记录的时间为40 s左右,并记录其在此时间内的平均流速和最大流速。结果见表1、表2和表3,其中水深均为55 cm。

表1 1、4、7、10四个点的率定结果Tab.1 Calibration results of four points 1, 4, 7, 10
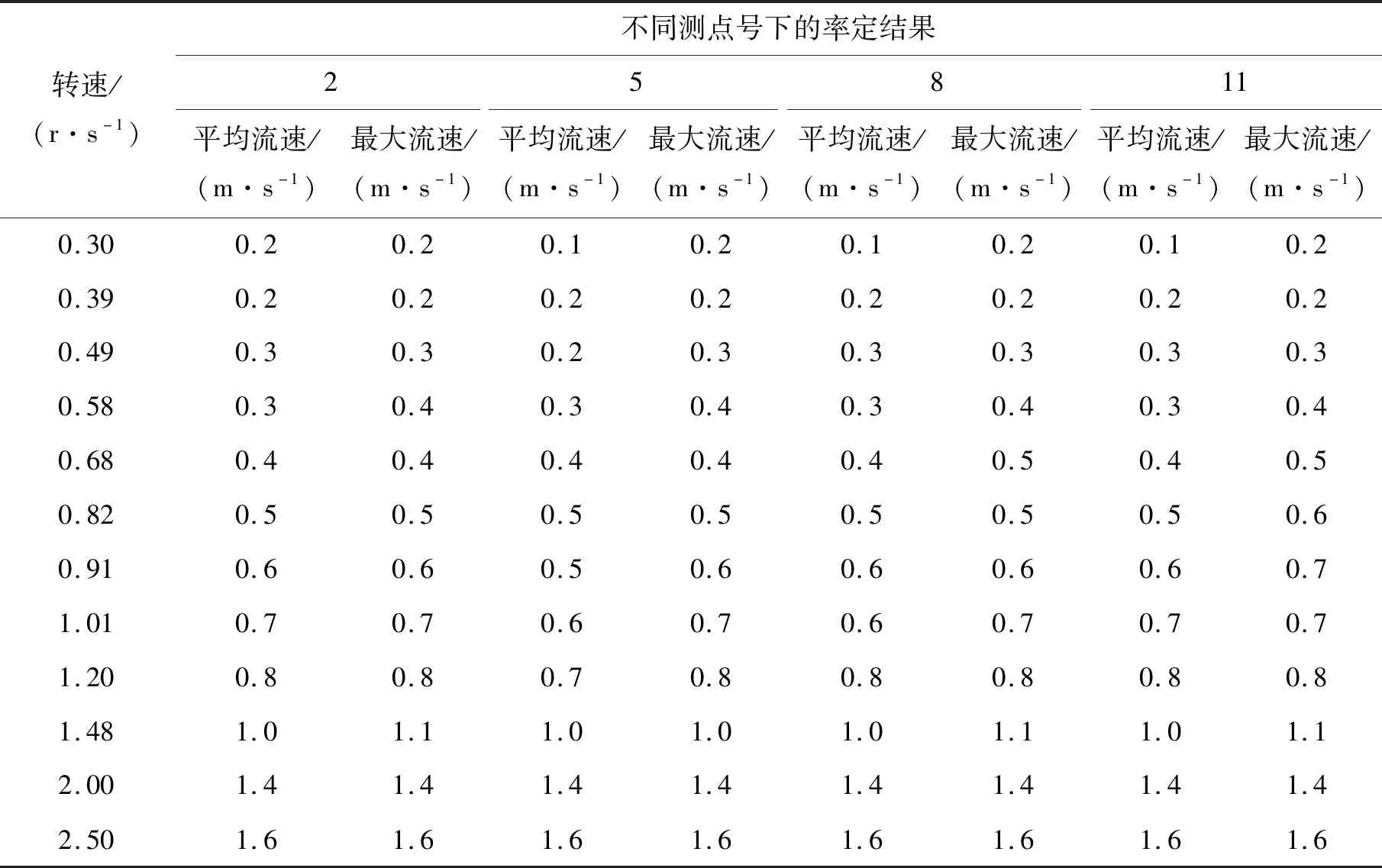
表2 2、5、8、11四个点的率定结果Tab.2 Calibration results of four points 2, 5, 8, 11
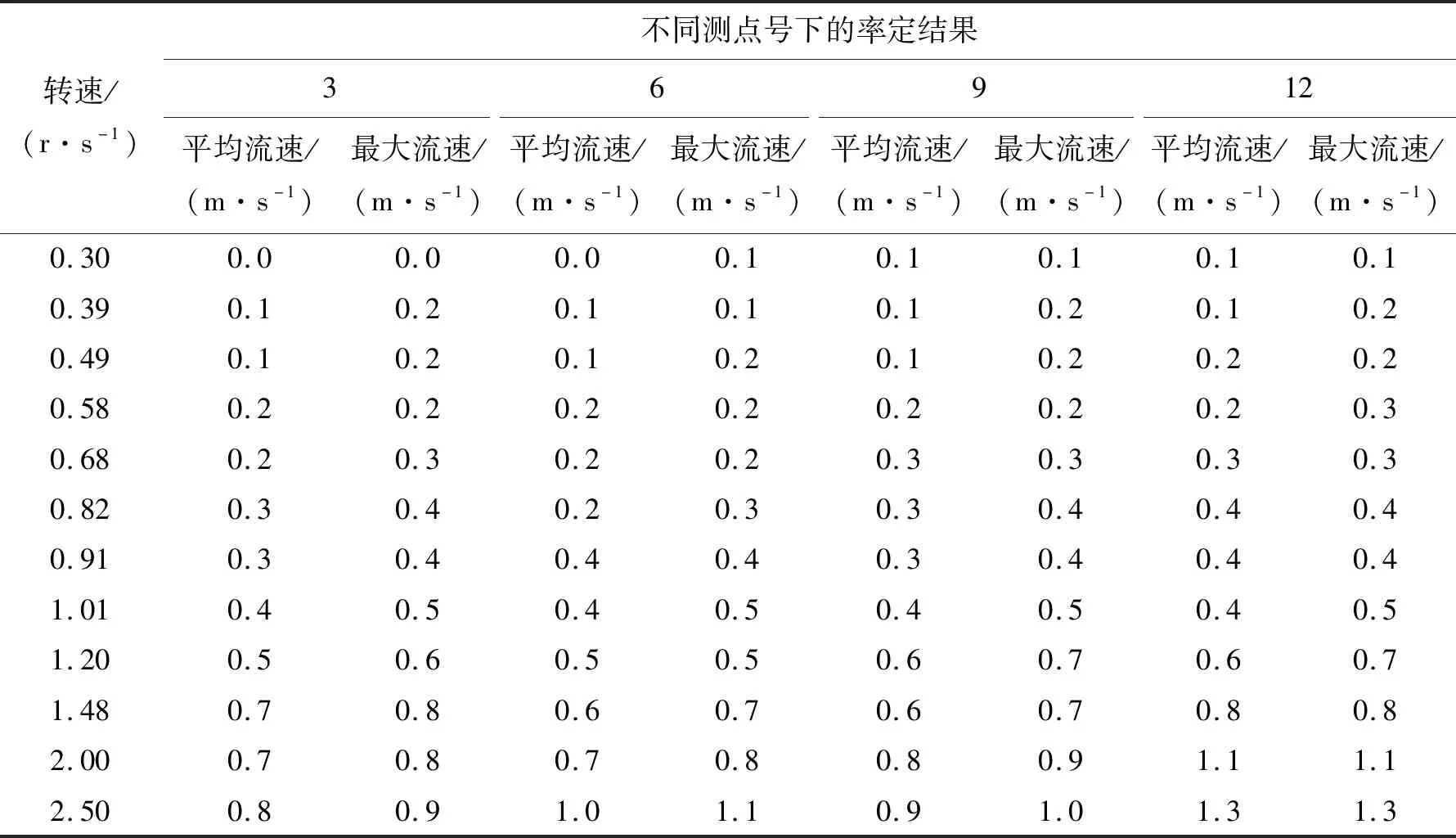
表3 3、6、9、12四个点的率定结果Tab.3 Calibration results of four points 3, 6, 9, 12
在率定过程中,发现无论水量多少,测点2(见图6)处的试样均为首先启动,验证了圆筒内部流速场的不均匀性。水流沿筒内叶轮的方向转动,水速分布主要由相对于叶轮的位置来决定,又因为2点的试样最先启动,故取各转速对应的2,5,8,11四个测点(见图6)最大流速值的平均值,得到转速与水速之间的换算关系。其换算关系式为:
y=0.679x-0.0103
(1)
式中:y为底部中心流速值(m·s-1);x为叶轮中心转速值(m·s-1)。
2.2 冲蚀剪应力计算方法
文献[18]认为在无法直接测量冲蚀率和剪应力的情况下,最有效的替代方法是使用Moody图(见图7)估计其剪应力。
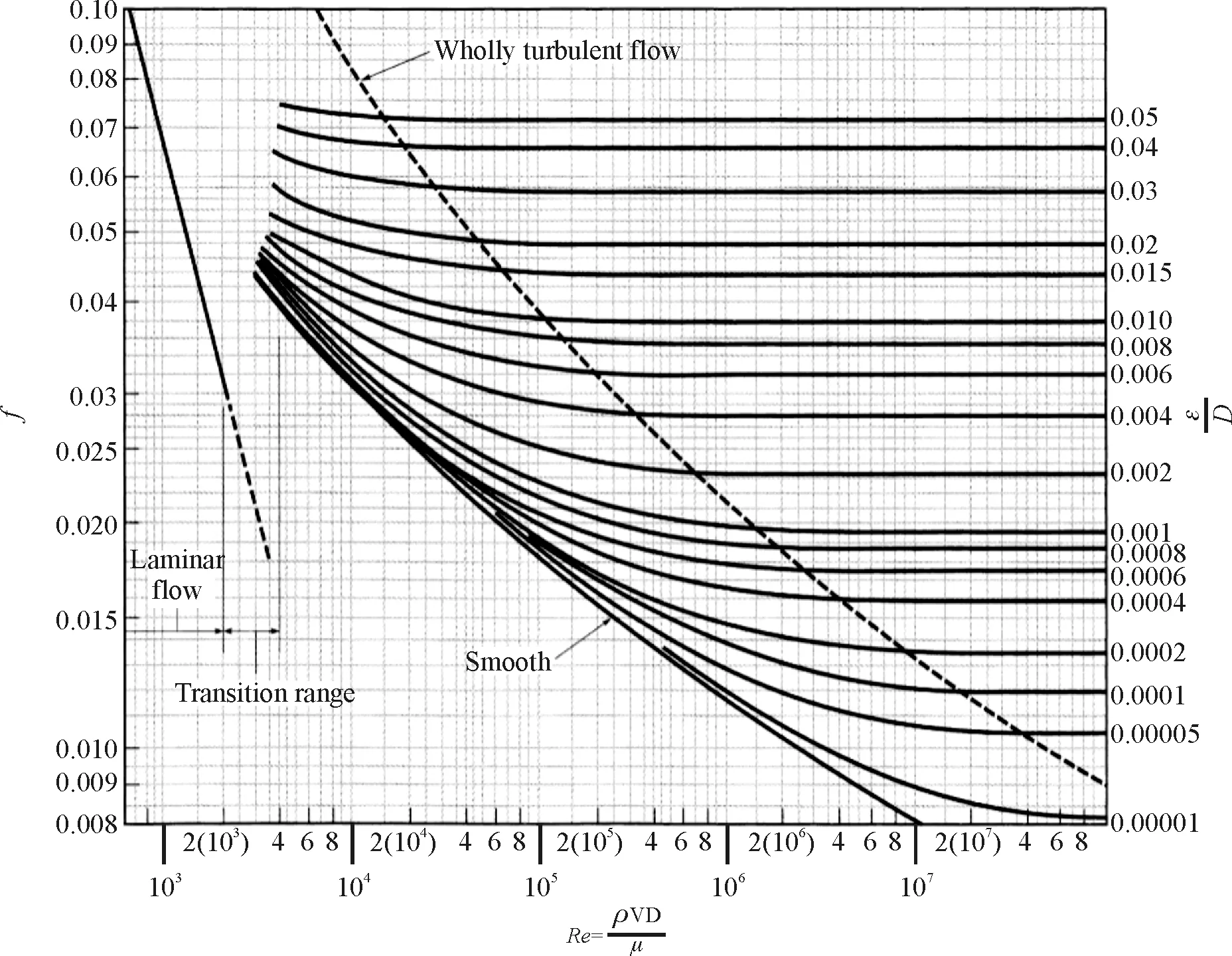
图7 Moody图Fig.7 Moody chart
本研究对圆筒型冲蚀试验设备采用Briaud[14]的剪应力计算公式:
(2)
式中:τ为剪应力(N·m-2);ρw为水的密度(1 000 kg·m-3);V为平均速度;f为摩擦系数。
Reynolds数Re计算公式为:
(3)
式中:D为管道的水力直径;v为水在25℃时的运动粘度(10-6m2·s-1)。水力直径D为水力半径R的4倍,水力半径由流动面积除以润湿周长来定义,此公式表示为:
D=2ab/(a+b)
(4)
则水力直径为:
(5)
当Re>100 000时,直接在Moody图中寻找对应的摩擦系数f。
当Re<100 000时,用:
(6)
此方程为Blasius方程,式(6)可计算摩擦系数,不必使用Moody图查询。
3 试验结果讨论
见图8,选用易贡的两种典型土料开展冲蚀试验,D50=8 mm,D50=10 mm。样品的面积控制为1 075 cm2和1 085 cm2,结果见图9。试验中土体天然密度分别为1.845 g/cm3和1.585 g/cm3,水深为55 cm。冲蚀率定义为单位时间内土料样品被冲走的高度,土料质量控制在4.00 kg和3.72 kg。
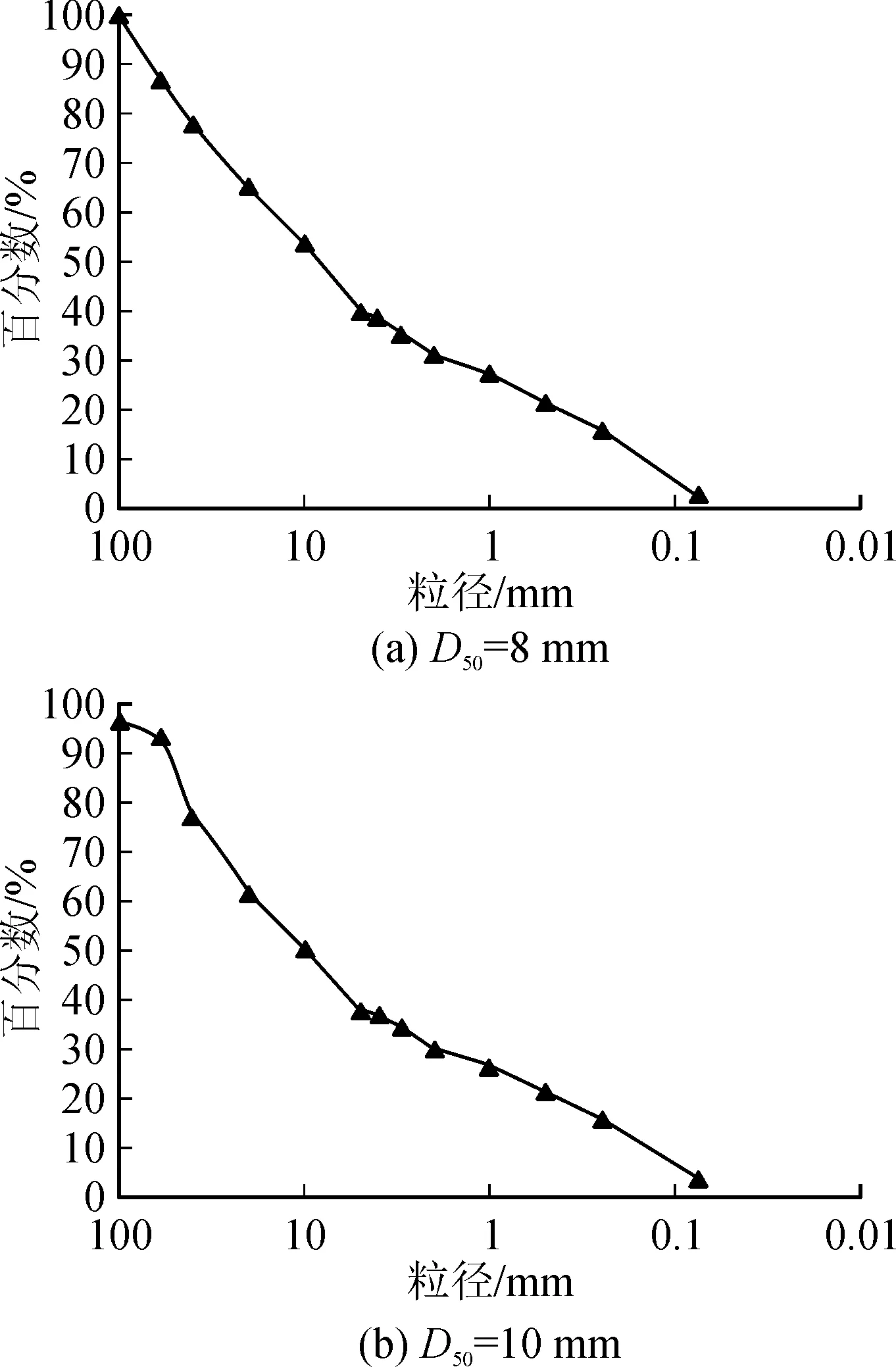
图8 易贡土料典型级配曲线Fig.8 Gain size distributions of two Yigong landslide dam materials
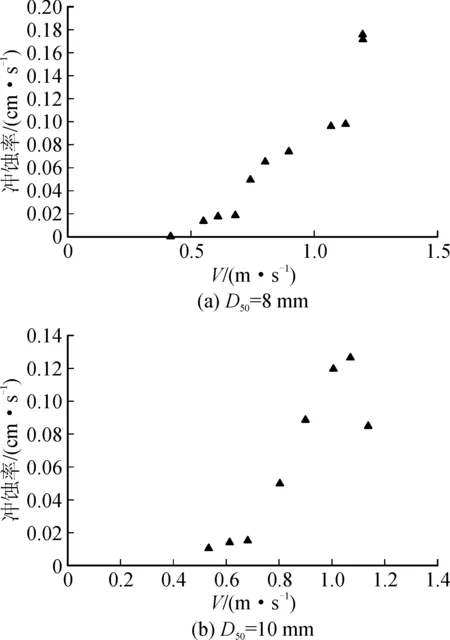
图9 典型粒径级配冲蚀率Fig.9 Erosion rate of particle size gradation
3.1 冲蚀率
Briaud[14]运用EFA设备对干净粗砂开展了冲蚀率研究。此土体的D50=3.375 mm,其冲蚀率最大为12 000 mm/h=0.33 cm/s,见图10,其冲蚀流速与冲蚀率呈双曲线函数关系。采用圆筒型冲蚀试验设备针对易贡的典型土料(D50=8 mm,D50=10 mm)开展冲蚀试验,试验结果见表4和表5。分别对以上数据运用R语言进行线性回归,建立冲蚀流速和冲蚀率之间的关系式,见式(7)和式(8)。
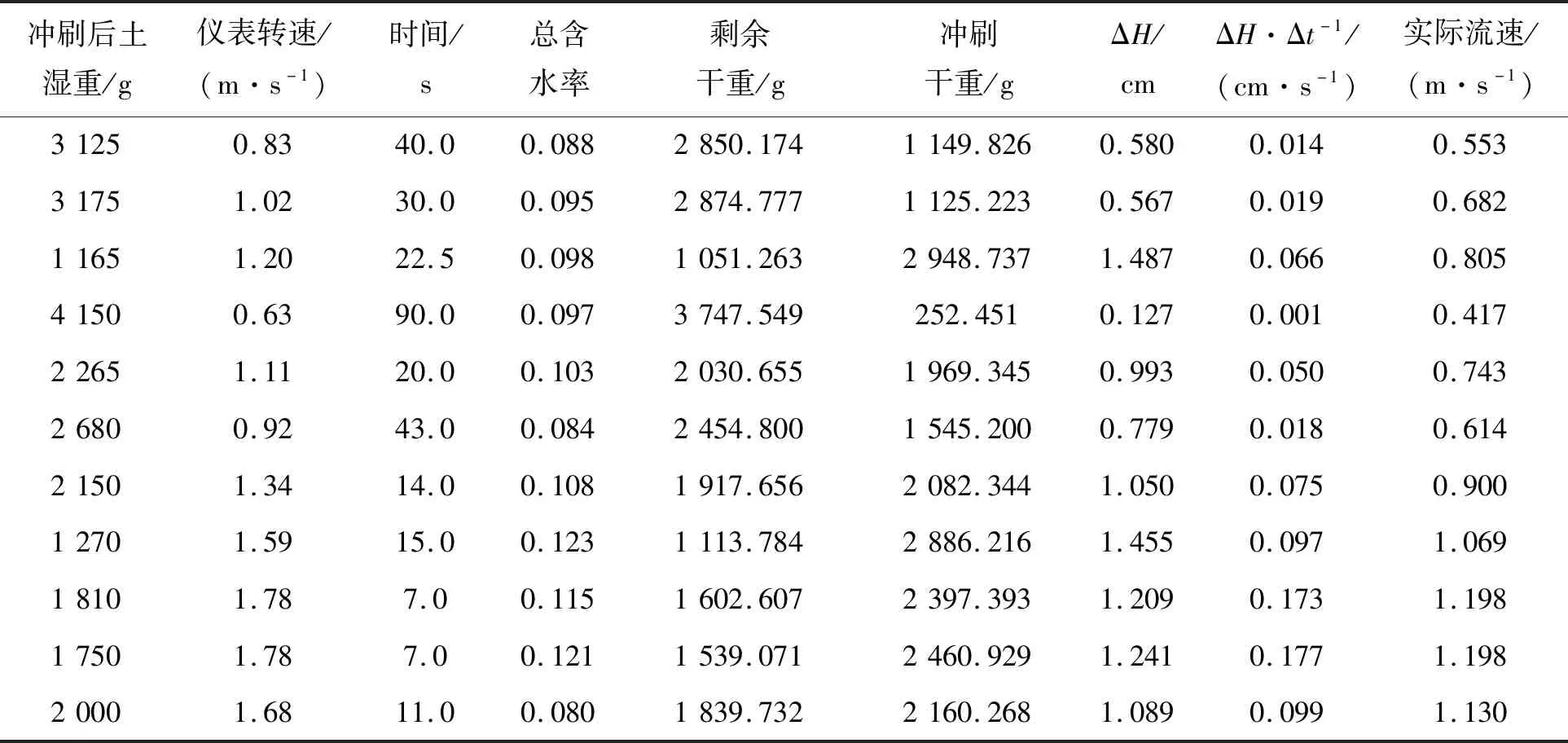
表4 粒径级配D50=8 mm冲蚀率Tab.4 Erosion rate of particle size gradation D50=8 mm
表5 粒径级配D50=10 mm冲蚀率Tab.5 Erosion rate of particle size gradation D50=10 mm
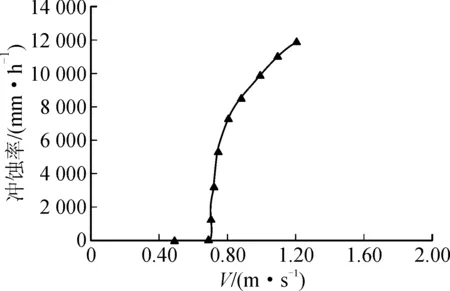
图10 砂土的冲蚀曲线Fig.10 Erosion curve for coarse sand
冲蚀流速与冲蚀率的关系,经回归后当D50=8 mm时:
(7)
当D50=10 mm时:
(8)
式中:v为冲蚀流速(m/s),y为冲蚀率(m/s)。
由图10可知,冲蚀流速与冲蚀率之间呈双曲线函数关系,试验中得到冲蚀率的最大值为0.17 cm/s,试验结果中的量级和图10中关于干净粗砂的量级一致,数值略小于文献中0.33 cm/s的数值。之所以出现此情况是因为EFA试验选用的材料为干净粗砂,而易贡主要堆积区材料除了块石、砂之外还包含一些粉尘及碎屑,所以试验结果稍小于Briaud[14]的数值。
Briaud[14]提到,EFA设备中的相同平均速度为1 m/s,砂的冲蚀率约是粘土的1 000倍,表明不同土体的冲蚀率可能存在较大差异。文献中提到干净的砂和砾石的冲蚀率数值量级为104mm/h,与本文试验结果一致。
综上所述,试验结果显示冲蚀流速与冲蚀率呈双曲线函数关系,且有很大的相关性,通过结果分析认为圆筒型冲蚀试验设备的可靠性值得信赖,也验证了冲蚀率试验结果的可靠性,可用来开展冲蚀剪应力研究。
3.2 冲蚀剪应力
参照EFA计算公式、圆柱的剖面为长方形,计算湿周,参考公式(2)~(6)计算剪应力,并采用回归方程寻找冲蚀流速、冲蚀率和冲蚀剪应力τ之间的关系。其冲蚀流速、冲蚀率和冲蚀剪应力之间关系见表6和表7。
表6 D50=8 mm时冲蚀速度与冲蚀剪应力的关系Tab.6 Relationship between velocity and critical shear stress in D50=8 mm

表7 D50=10 mm时冲蚀速度与冲蚀剪应力的关系Tab.7 Relationship between velocity and critical shear stress in D50=10 mm
冲蚀流速与冲蚀剪应力的关系,经回归后当D50=8 mm时指数曲线为如下:
(9)
当D50=10 mm时指数曲线为如下:
(10)
式中:τ为冲蚀剪应力(N·m-2);y为速度(m·s-1)。
3.3 冲蚀率剪应力模型
本课题组[19]基于唐家山实测的冲蚀率,认为土体材料抵抗冲蚀时,不应有无限“强度”,建议采用双曲线模型,其形式如下:
(11)
式中:v为扣除临界剪应力后的剪应力:
v=k(τ-τc)
(12)

双曲线模型的冲蚀率是具有物理意义的,认为土体包含一定的强度,当冲蚀达到一定程度后,将不再增加(见图11)。即双曲线有一当v接近无限值时的渐进线,即dz/dt的极值1/b。其中单位变换因子k为100,其含义为v等于0时曲线的斜率。

图11 堰塞湖土料冲蚀剪应力与冲蚀率的关系图Fig.11 Relationship between erosion shear stress and erosion rate of dam-lake soil
在所有溃决洪水分析方法中,研究人员多选用继承了泥沙-水力学领域中开发的土体冲蚀模型,如Engelund-Hansen、Meyer-Peter-Mueller及Einstein-Brown,分别应用于计算机程序MIKE11模型、BREACH模型和BEED模型。这些模型多用来评价低流速河床上的泥沙输运模式,高速溃决洪水过程中的土体冲蚀行为很少研究。由于流速的定义关系,冲蚀剪应力与冲蚀率有很大的相关性,较快的流速产生较大的冲蚀剪应力。上述大多数用于测量粘性土体和岩石的冲蚀率分析表达式包含大量参数。Trammell[20]认为基于这些变量参数准确的预测其相关性是不切实际的,而且评估大量参数导致成本过高。
Einstein[21],Partheniades[22],van Prooijen 和 Winterwerp[23]都认为冲蚀率可由与冲蚀剪应力相关的函数关系式表示。Slagle[24]还认为可运用类似EFA-SRICOS或Miller-Sheppard模型[24-25]方法,使用纯经验公式模拟冲蚀率剪应力关系。因此,纯粹的经验方法可用来拟合冲蚀率-冲蚀剪应力关系。van Prooijen和Winterwerp认为在低于原定义的临界剪应力时仍可能发生冲蚀;在大于临界应力时,该线性近似仍是有效的。因此,通过首先计算冲蚀率,再绘制其与剪应力的函数关系图,建立冲蚀率与冲蚀剪应力的冲蚀模型。
Briaud[14]提出,在干净的砂和砂砾中,影响τc的主要土体参数是由D50引起的。本文改变D50的大小,研究冲蚀率和冲蚀剪应力的关系。冲蚀率与冲蚀剪应力数值见表3和表4。通过对冲蚀率和冲蚀剪应力的关系回归后公式见下。
D50=8 mm:
(13)
D50=10 mm:
(14)
式中:τ为剪应力(N·m-2);y为速度(m·s-1)。
本课题组[19]基于唐家山实测的冲蚀率,提出了冲蚀率-剪应力双曲线模型,认为土体材料抵抗冲蚀时,不应有无限“强度”。上述研究证实冲蚀率与剪应力之间呈双曲线函数关系。当剪应力较小时,冲蚀率与剪应力存在较强的双曲线函数关系。
4 结 论
土料冲蚀特性可以用水流引起的冲蚀剪应力和土料冲蚀函数(即冲蚀速率与剪应力曲线)表征。本文介绍了一种新型土料冲蚀测量系统,该测量系统包括一个圆筒型冲蚀试验装置(CETA)和一种计算剪切应力的方法。所研制的CETA具有空间小、耗水量少、流速高等优点,并能对D50小于30 mm的土体颗粒进行测量。运用此系统开展了易贡土料的启动流速、冲蚀率、冲蚀剪应力研究。
试验结果表明:该装置的冲蚀率结果可靠,与原有文献的冲蚀率数值处于同一量级,与Briaud的实验结果一致,可用来进行堰塞湖土料冲蚀率-剪应力分析;提出了堰塞湖土料冲蚀剪应力的精确计算方法,发现冲蚀率与剪应力呈现双曲线关系,建立了堰塞湖土料双曲线冲蚀模型,可应用于堰塞湖溃决分析模拟。
