无资料地区不同时间尺度下流量历时曲线推演及其规律分析
2020-12-14姬宏伟刘登峰栾金凯慕鹏飞
姬宏伟, 白 涛, 刘登峰, 栾金凯, 慕鹏飞
(西安理工大学 西北旱区生态水利国家重点实验室, 陕西 西安710048)
无资料地区的水文预测问题(Prediction in Ungauged Basins,PUB)一直是水文学研究的重点和难点,得到了国内外众多学者的广泛关注[1]。流量历时曲线(Flow Duration Curve,FDC)是反映流量在某一时段内(或年内某一季节、一年)超过某一数值持续天数的一种统计特性曲线,其纵坐标为日平均流量,横坐标为超过该流量的累计日数,即历时。如横坐标用历时相对百分数表示,则为相对历时曲线,或称保证率曲线[2]。水利工程在设计时常需获取FDC,以掌握工程所在地区的径流特征。但是,由于部分中小型规模的水利工程往往位于无实测径流资料地区,故无法直接由实测径流资料得到FDC[3]。
长期以来,估计无资料地区FDC的方法主要分为两类[4]:一是基于水文过程和统计的方法预测无资料地区FDC;二是根据物理成因机制,辅以流域水文模型以及降雨径流相关假设,最后将有资料地区的模型参数移植到无资料地区。其中,统计的方法主要包含回归方程[5-6]、地质学统计方法[7]等,这些统计方法因操作简单、易于实现而备受青睐[8-9]。例如,杨邦等[10]采用FDC作为水文模型的拟合目标,从而确定无资料地区的参数,为无资料地区水文模型参数的区域化提供了新思路;黄国如[11]通过对FDC的深入分析,得到了区域化的FDC,为无资料地区的径流预测提供了一条简单有效的途径。
然而,上述研究主要集中在一定的时间尺度,很少涉及或分析不同时间尺度下FDC之间的关系,而不同时间尺度的FDC在水文学中的用法不同[12],因此,本文着重研究不同时间尺度下FDC之间的关系。本文以渭河流域支流8个代表性水文站为研究对象,利用单一概率分布模型进行日径流序列模拟,阐明不同时间尺度下FDC的相关关系,以预测无资料地区或仅有大时间尺度数据地区的日径流过程。研究成果可为无实测资料地区FDC的推演提供一条简便可靠的途径,并为无资料地区的水利工程规划、设计、施工和运行管理提供重要支撑。
1 区域概况及基本资料
渭河是黄河最大的支流,渭河流域位于黄土高原,分为西部黄土丘陵沟壑区和东部关中平原区两部分。受地形等因素影响,流域产汇流体现出明显的区域特征。流域内降水分布由东南向西北递减,南部秦岭山麓降水丰富,年最大降水量在1 000 mm以上,降水量随高程的降低而急剧减小,平原区年降水量约500 mm。研究区资料包括渭河流域支流8个水文站(武山站(H01)、秦安站(H02)、天水站(H03)、凤阁岭站(H04)、安头站(H05)、黑峪口站(H06)、柳林站(H07)、马渡王站(H08))2001—2016年的实测日平均流量数据,该数据来源于中华人民共和国水文年鉴(第4卷第7册)[13]。8个水文站的基本资料如表1所示,研究区域如图1所示。
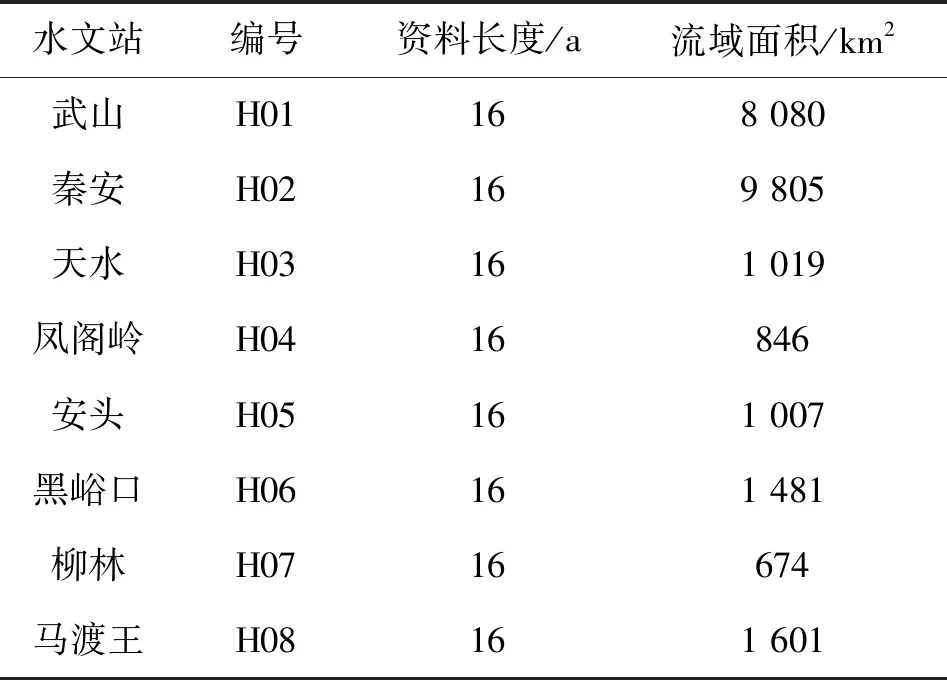
表1 各站的主要统计参数Tab.1 Main statistical parameters of each station

图1 水文站和研究区域图Fig.1 Hydrological station and study area map
2 研究方法
在日时间尺度上,由于日径流过程是一个复杂的时间序列,流量值范围横跨多个数量级,因而很难找到可以准确描述日径流的概率分布,因此,对日径流序列的模拟需要具有多个参数的复杂概率分布来完成[10]。
有多种方法可以对FDC进行建模,且不同方法适用的区域不同[14]。本文在以往研究的基础上,针对径流序列的特点、模型的复杂度以及分布参数的个数,选取了三种分布函数来估计年内日径流序列的概率分布,如表2所示,利用建模FDC参数比较(M-FDC-P)[14],通过计算不同时间尺度下经验FDC参数,再基于Nash-Sutcliffe效率(NSE)和均方根误差(RMSE)评价拟合效果的优劣,得出适合该地区的最优分布函数及参数,最终分析参数相关性以得到不同时间尺度下FDC之间的相关关系。

表2 分布函数Tab.2 Distribution function
M-FDC-P方法的步骤为:
步骤1 经验FDC的估算。常用的绘制流量历时曲线的方法主要分为总历时法和多年平均历时法。总历时法是对记录期内所有日径流序列按照升序排序,然后求出各个流量的经验频率,从而得到 FDC 曲线;多年平均历时法(又称年内流量历时曲线)是先求出每年的 FDC,然后根据年内 FDC 求出中位数值(或均值),并给出相应的置信区间,其优势在于是利用统计的方法因而不受记录期内异常值的干扰(异常枯水和洪水)。总历时法能够反映流域的真实径流特性,而多年平均历时法则反映流域多年平均的径流特性(该法FDC 曲线是处理后的曲线)。因此,为了更真实地反映流域径流情况,本文将采用总历时法来绘制流量历时曲线图。
为了获得每个流量的超过概率,使用weibull分布,因为它提供了超出概率的无偏估计,而且可以不考虑满足底分布序列样本的排序[15]:
(1)
式中:i代表序列的排序位置;n代表记录期年数。Vogel 和 Fennessey[15]给出了几种非参数方法用于绘制小样本量的 FDC 图,然而考虑到本文的样本量较大,因此选择weibull分布。
步骤2 拟合经验FDC。对于各站点不同时间尺度下的FDC,分别利用指数函数、Gamma函数、对数正态分布进行拟合,得到各个分布的参数。
步骤3 评估FDC模型的可靠性和适用性。通过拟合得到具体的参数,就可以绘制由参数确定的FDC。为了评估拟合FDC的优劣性,使用Nash-Sutcliffe效率(NSE)和均方根误差(RMSE)进行评价,得到最优概率分布。
步骤4 参数相关性分析。通过分析不同时间尺度下最优概率分布参数的变化规律和评估分布参数之间的相关性来分析不同时间尺度下FDC之间的关系。
3 实例计算与分析
3.1 不同时间尺度下经验FDC的变化
为了阐明FDC随时间尺度的变化规律,分析各站在不同时间尺度下(1 d、7 d、15 d、30 d、90 d和365 d)的经验FDC(分别对应于每日、每周、半个月、每月、每季度和年度FDC)的变化规律。限于篇幅,本文只给出武山站在不同时间尺度下的经验FDC,如图2所示。

图2 武山站经验流量历时曲线随时间尺度的变化Fig.2 Empirical flow duration curve (FDC) variations with time scales for Wushan Station
由图2可以看出,经验FDC随时间尺度变化缓慢,FDC在1 d的时间尺度上具有最大的斜率,然后随着时间尺度变大,曲线变得逐渐平坦;当时间尺度在1 d~30 d时,经验FDC非常相似;当时间范围大于90 d时,FDC会出现明显的差异。其余7个站点的经验FDC的变化规律与武山站相同。
3.2 分布函数的优选
利用8个站点的日径流数据,从表2所列的3个分布函数中筛选出研究区域的最佳分布函数。表3、表4分别给出了研究区域内各站在不同时间尺度下(1 d、7 d、15 d和30 d)的经验FDC的NSE和RMSE值。
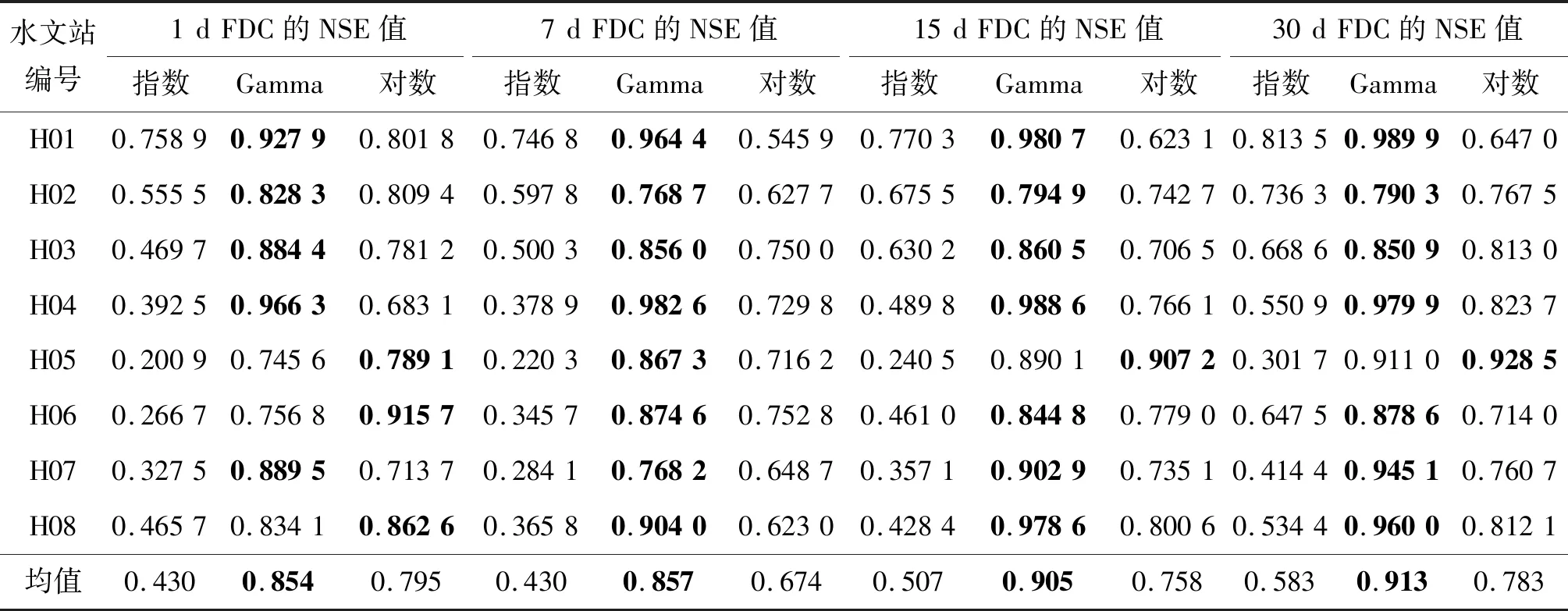
表3 不同站点各分布函数的NSE值Tab.3 NSE values of distribution functions at different sites

表4 不同站点各分布函数的RMSE值Tab.4 RMSE values of distribution functions at different sites
本文使用Nash-Sutcliffe效率(NSE)和均方根误差(RMSE)来评价模型的性能。NSE是一个归一化指标,其值越接近于1表明模拟效果越好。图3给出了8个站点不同时间尺度下FDC模拟效果的NSE值和RMSE值箱线图,从箱线图可以直观看出这三种分布的模拟效果。对于绝大多数站点,Gamma函数具有NSE高、RMSE低的特征,其不同时间尺度下NSE和RMSE的中位数值都分别在0.85以上和0.04以下。根据以往研究成果[16],可判定Gamma函数的性能最好,其次是对数正态分布函数,最差的是指数分布函数。综上所述,在分布函数选取的过程中,推荐使用Gamma分布函数作为拟合日径流的概率分布。
武山站和秦安站是渭河流域支流控制面积最大的两个站,代表性较强。限于篇幅,本文选取武山站和秦安站作为典型站点,将1 d流量历时曲线拟合值与实测值进行对比分析。结果如图4、图5所示,可以看出:

图4 武山站实测和拟合流量历时曲线Fig.4 Measurement and fitting flow diachronic curve of Wushan Station

图5 秦安站实测和拟合流量历时曲线Fig.5 Measurement and fitting flow diachronic curve of Qinan Station
1) 利用Gamma分布拟合的FDC与实测的FDC比较吻合;
2) 由图6可得,利用Gamma分布拟合的FDC,除了枯水部分的模拟值与实测值差异较大外,其它模拟值均在实测值的30%相对误差区间内,符合精度要求。

图6 武山站实测与Gamma分布拟合的流量历时曲线Fig.6 Flow duration curve fitted with measured and Gamma distribution at Wushan Station
3.3 基于 M-FDC-P 方法的 FDC 关系研究
对日径流序列在不同时间尺度上取平均值,拟合成Gamma分布,并研究了Gamma分布参数之间的关系。如前所述,1~30 d时间尺度下的经验FDC非常相似,可能具有很强的相关性,因此,本文将研究集中在1~30 d时间尺度上,且大时间尺度的流量数据更容易获取。
为了评估Gamma分布参数随时间尺度的变化,图7给出了1~30 d时间尺度上8个水文站的FDC的三个Gamma分布参数的平均值。
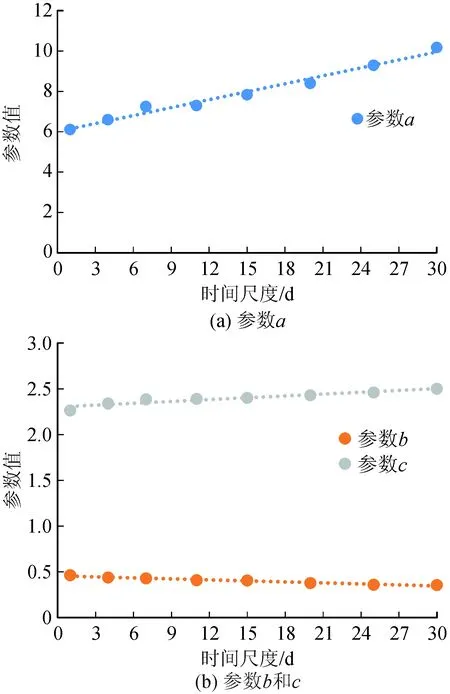
图7 1~30 d时间尺度下三个Gamma分布参数平均值的变化Fig.7 Change of the average value of the three Gamma distribution parameters in the time scale of 1~30 d
由图7可看出,所有参数都随着时间尺度逐渐变化,呈现出明显的变化趋势。对于参数b,它随时间尺度增加而减少,在1 d时间尺度上最大为0.46,在30 d时间尺度上最小为0.35。参数a和c非常相似,均随着时间尺度的增加而增加,但参数a的增加趋势更为明显。
研究不同时间尺度下Gamma分布参数的相关性。表5给出了1 d、7 d、15 d和30 d时间尺度下三个参数之间的线性相关系数。

表5 三种Gamma分布参数在不同时间尺度上的线性相关系数Tab.5 Linear correlation coefficients between three Gamma distribution parameters in different time scales
对于参数c,所有相关系数均超过0.64,表明参数c在1~30 d时间尺度内存在较高的相关性。对于参数a和b,随着时间尺度的增大,1 d FDC与其他时间尺度之间的线性相关系数逐渐减小。与参数c相比,不同时间尺度下参数a的相关性较弱。
从参数a和参数b来看,在1~30 d时间尺度之间其线性相关系数显著低于参数c,其中1 d与30 d的相关系数分别为0.297 9和0.479 8,均低于0.5,说明相关性较弱。
所有参数中,参数c线性相关系数最高,其最低时(1 d到30 d时间尺度之间)仍然超过0.6,显示出较强的相关性。
4 结论与展望
本文以渭河流域8个水文站为研究对象,运用M-FDC-P方法,对研究区域8个站点不同时间尺度上的FDC进行研究。
1) 不同时间尺度下,经验FDC随时间尺度的增加而逐渐平坦,当时间尺度在1~30 d时,经验FDC非常相似;当时间范围大于90 d时,FDC会出现明显的差异。当利用单一概率分布拟合1~30 d时间尺度的FDC时,其在非洪水和非枯水部分的拟合效果较好,总体上能得到令人满意的精度,但在FDC的尾部模拟效果较差,这表明利用单一概率分布估计整个日径流变化过程是比较困难的,尤其是对于日径流序列尾部的变化。
2) 分布函数优选结果表明:Gamma分布为最优分布,其次是对数正态分布函数,最差的为指数分布函数。对于绝大多数站点,Gamma函数均具有NSE高、RMSE低的特征,其不同时间尺度下NSE和RMSE的中位数值都分别在0.85以上和0.04以下。因此,以NSE和RMSE作为判据,选取 NSE 值最大、RMSE值最小的概率分布作为最优分布,故本文推荐使用Gamma分布函数作为拟合日径流的概率分布。
3) 通过分析1~30 d时间尺度下3个Gamma分布参数的相关关系,发现不同时间尺度参数之间的线性相关系数随着时间尺度的增大而减小。其中参数c的相关性最好,除1 d与30 d最大时间尺度差异下参数c的相关系数为0.641外,其他相关系数均高于0.8;而对于参数a和b,其1 d与30 d的相关系数分别为0.297 9和0.479 8,均低于0.5,说明相关性较弱。
上述分析研究表明,当利用一个特定的概率分布对较大时间尺度FDC进行建模时,可以考虑通过流量分布的内在关系得到日径流分布。本文中发现的关系可作为区域回归模型的重要补充,用于估计无资料地区的日径流过程,为今后研究区域内供水工程的规划及水资源优化配置提供设计依据。
但是,水文过程是一个具有物理机制的自然过程,本文只利用特定的概率分布来对FDC进行建模,无法得到准确的模拟日径流过程的概率分布,因此,在今后的研究中,可以考虑加入具有物理意义的水文模型来进行模拟,未来的研究还将考虑分布参数的区域化,以便综合利用7 d、15 d、月流量数据和其他信息来推演完整的日径流过程。
