一种用于同塔双回线故障定位的新相模变换法

王守鹏，赵冬梅，袁敬中，高 杨

(1. 国网冀北电力有限公司经济技术研究院，北京100038；2.华北电力大学电气与电子工程学院，北京102206)

同塔双回输电线路[1-2]架设于同一铁塔，线间距离紧凑，具有占地少、输送能力强、投资效益高等优点[3]，因此，近年来同塔双回输电线路在工程领域得以广泛应用，其故障定位方法亦受到广大学者的关注，并已经取得了大量的科研成果[4-11]。其中，单端故障定位法[4-5]仅使用一端的电气量，采集数据量小，但结果受过渡电阻、系统阻抗的影响严重；双端故障定位法[6-11]因引入双端的电气量，从原理上消除了过渡电阻、系统阻抗对结果的影响，并且随着电力通信技术的发展，应用前景良好。从解耦方法来看，目前解耦计算中比较经典的相模变换有对称分量、Clarke、Karenbauer等变换[6]。其中，对称分量变换可用正序分量反映各种故障类型，但其矩阵因子含有复数，使得故障分析中的计算量大大增加；Clarke变换、Karenbauer变换的矩阵因子均为实数，实数运算具有计算简单、计算量小的优点，但Clarke变换、Karenbauer变换无法用单一模量反映各种故障类型，在故障定位时要与选相配合或采用双模量分析[7]。

本文从三相输电系统出发，推导新的相模变换矩阵。结合均匀换位的输电线路的相模变换矩阵的数学性质，根据三相系统和六相系统之间的关系，推导出了一种新的双回线相模变换矩阵。该变换矩阵的运算因子全为实数，用于相模变换时可用单一模量反映各种短路故障。用此变换矩阵将同塔双回线解耦，可在某一模量下实现同塔双回线发生各种短路故障时的故障定位。大量ATP-EMTP仿真结果表明，故障定位结果不受故障类型、过渡电阻和数据不同步的影响，具有较高精度。

1 相模变换

1.1 三相系统相模变换矩阵

对于图1所示的三相系统，在线路均匀换位情况下，线路参数对称，且参数矩阵为平衡矩阵，则有：

(1)

其中平衡参数矩阵为：

解耦计算就是使Z对角化，求解特征方程det(Ζ-λiI)=0，可得：

(2)

则对应于特征值λi的特征向量为Ti=(t1i,t2i,t3i)T，i=1,2,3。令矩阵T=(T1,T2,T3)，则有可逆矩阵T-1、对角阵Λ，使T-1ZT=Λ，其中Λ=diag(λ1,λ2,λ3)。

由特征值和特征向量的数学性质，有：

(Ζ-λiI)Ti=0

(3)

把式(2)中的λ1代入式(3)，可求得：

t11=t21=t31

(4)

同理，把式(2)中的λ2、λ3代入式(3)，可求得：

t12+t22+t32=0

(5)

t13+t23+t33=0

(6)

对于任意三阶矩阵，如果满足式(4)～式(6)，则均可作为三相系统的相模变换矩阵。验证易知，对称分量变换、Clark变换、Karenbauer变换的矩阵均满足式(4)～式(6)。

基于上述分析，对于图1所示三相系统，根据式(4)～式(6)可构造用于三相系统的相模变换矩阵：

(7)

其逆矩阵为：

(8)

利用矩阵T可将存在互感的三相系统解耦，得到3个相互独立的0、1、2模分量。用T将三相系统中的电流相量变换为模量的形式：

(9)

将式(8)代入式(9)，展开可得：

(10)

表1给出了各种短路故障下用变换矩阵T做解耦计算取得的电流模分量值。

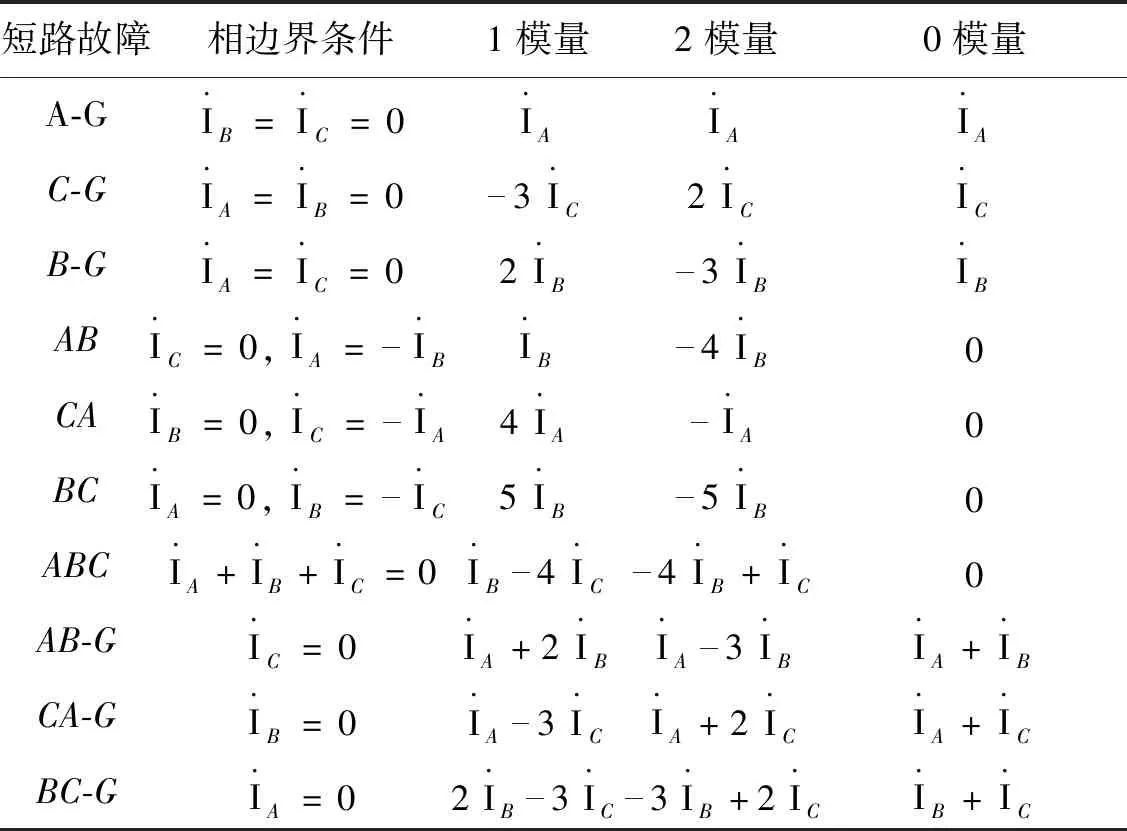
表1 各种短路故障下的电流模分量Tab.1 Current modulus components under all kinds of fault types

由表1可知，通过变换矩阵T解耦而得的1模量和2模量始终存在，因此可以利用解耦后的1模量或2模量进行故障分析，从而完成各种短路故障情况下的故障定位。

1.2 六相系统相模变换矩阵

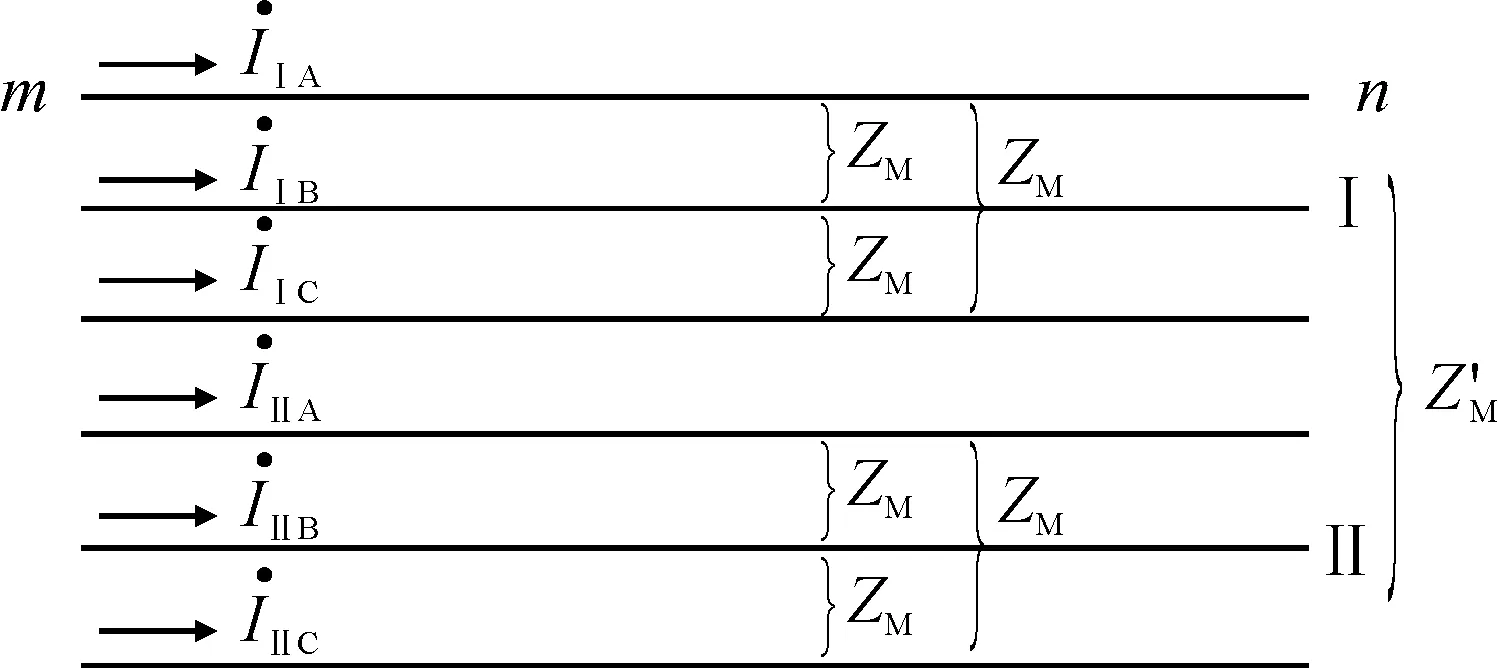
图2 六相系统图Fig.2 Schematic of six-phase system

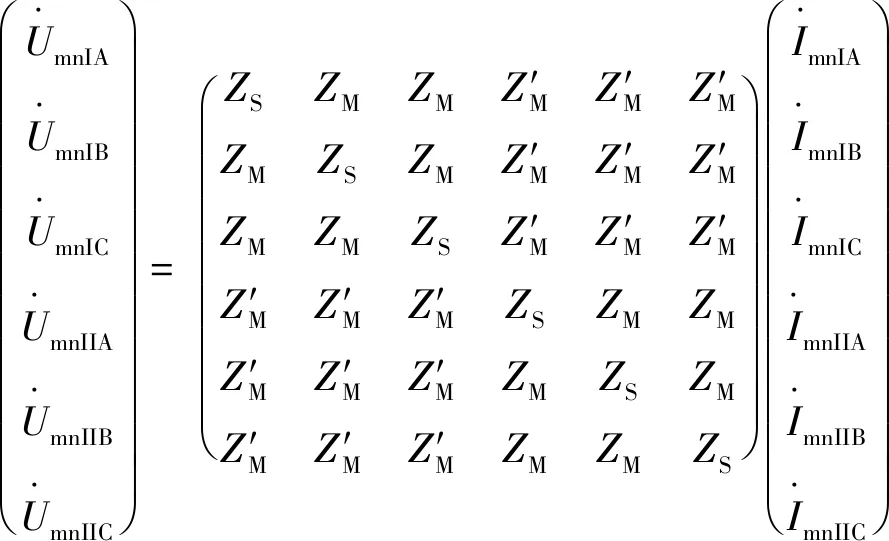
(11)

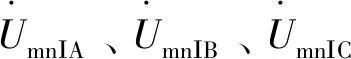
结合文献[3]、[8]采用的六序分量法线间解耦矩阵P将式(11)的电压、电流相量分解为同、反向量，以及将Ⅰ、Ⅱ回线之间解耦，得：

(12)

式中：

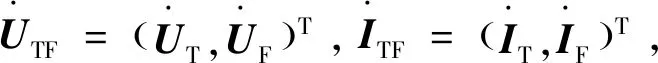
将式(12)表示为同向量和反向量的形式，即：

(13)

式中：

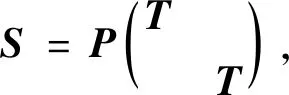
由此得到解耦后的模量与相量之间的关系：

(14)

式中：

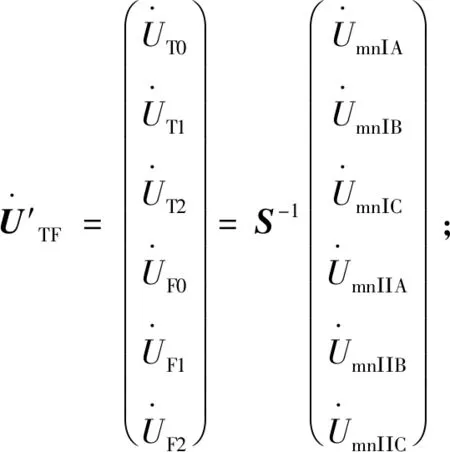
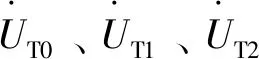
由式(14)可知，存在互感的双回线通过变换矩阵S变换为6个相互独立的模量，而且矩阵S的运算因子均为实数，实数不但可简化运算，而且能够大大减少运算量。线间解耦矩阵P的引入，既保留了Ⅰ、Ⅱ回线间的关联性，又具有类似六序分量法变换矩阵的性质，如应用同向网1模量，故障定位可以不受短路故障类型的束缚；结合变换矩阵T的性质，相模变换矩阵S解耦后的同向网1模量和2模量在发生各种类型短路故障情况下均存在，从而可以应用同向网1模量或2模量实现各种短路故障下的故障定位。

2 同塔双回线的双端故障测距原理

通过上述对六相系统的相模变换矩阵的分析，可使用相模变换矩阵S来对同塔双回线进行解耦，并应用某一模分量来完成故障定位。首先以单相系统为例推导故障定位算法，输电线路采用分布参数线路模型，线路的故障示意图如图3所示。

图3 线路故障示意图Fig.3 Schematic diagram of line fault

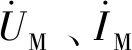
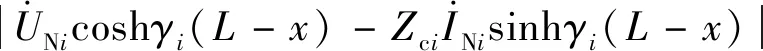
(15)

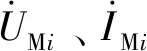
对于式(15)，令F(x)=0，可得故障定位方程。

根据叠加原理，故障定位亦可采用线路两侧电压、电流故障分量进行分析，从而消除故障定位使用工频电气量时所受负荷电流的影响[12-13]。则式(15)可改写为相应故障分量表示的形式：

(16)

对式(16)求解，具体方法采用迭代搜索法[14]，选取步长Δx，分别从线路双端推导沿线电压幅值分布曲线，两条曲线交点的位置则为故障点的位置。需要说明的是，Δx取值越小，故障定位精度越高，但同时计算量也越大，计算时间亦越长。对于故障定位而言，并不要求有很高的实时性，因此有足够的时间来进行运算，实际计算中步长可根据工程需要进行选择。

式(16)所示的故障定位方程计算的是模值差，是根据在故障点处模值差为零而求得故障距离。对于同塔双回线系统，可应用某一模分量来实现故障定位。应用前文介绍的六相系统相模变换矩阵S进行解耦计算，采用同向网1模量或2模量，故障定位可以不受故障类型的束缚。需要说明的是，所采用的同向网1模量或2模量，在不同故障条件下线路双端测量点处模值会有所差别，但对于式(16)而言，故障点处模值差始终为零。考虑工程实际应用于故障定位的模分量在不同故障条件下的模值差别不是双端故障定位计算的影响因素，因此本文仅应用同向网1模量或2模量进行计算亦不会影响到工程实际应用。

3 算例仿真分析

采用ATP-EMTP搭建同塔双回线模型进行仿真分析，如图4所示。系统及线路参数设置为：

图4 同塔双回线仿真模型Fig.4 Simulation model for double-circuit lines

线路长度：L=250km；

单位正序阻抗：Z1=0.038 7+j0.309 8 Ω/km；

单位零序阻抗：Z0=0.186 5+j0.731 6 Ω/km；

单位正序导纳：jωC1=j3.764 0 uS/km；

单位零序导纳：jωC0=j2.037 5 uS/km；

单位零序互阻抗：ZM0=0.147 8+j0.421 8 Ω/km； 单位零序互导纳：jωCM0=j0.542 9 uS/km。

本文为获取较高的精度，Δx取值与定位精度一致，为0.1 m。故障定位采用双端电压、电流的故障分量。解耦计算采用所提的相模变换阵S，并应用求得的同向网1模量进行故障定位。以100 kHz采样频率对故障后的第二周波进行采样，并采用全周傅氏算法进行滤波。

首先对本文所提相模变换矩阵的有效性进行仿真验证。表2列出了同塔双回线在几种比较典型的短路故障下，与六序分量变换矩阵的对比结果，其中相间和接地的过渡电阻均设为50 Ω，故障距离设为50 km。可见，本文所提的相模变换法能够在单模量下完成测距，并满足故障定位的要求。

表2 故障定位比较结果Tab.2 Comparison results of fault location

表3列出了同塔双回线在故障距离为50 km、90 km、160 km和230 km时，发生几种比较典型的短路故障情况下的故障定位结果，其中相间和接地的过渡电阻均设为50 Ω。由表3可知，同塔双回线在发生不同短路故障情况下，该算法均可以满足故障定位要求，并可避免短路故障类型的影响。

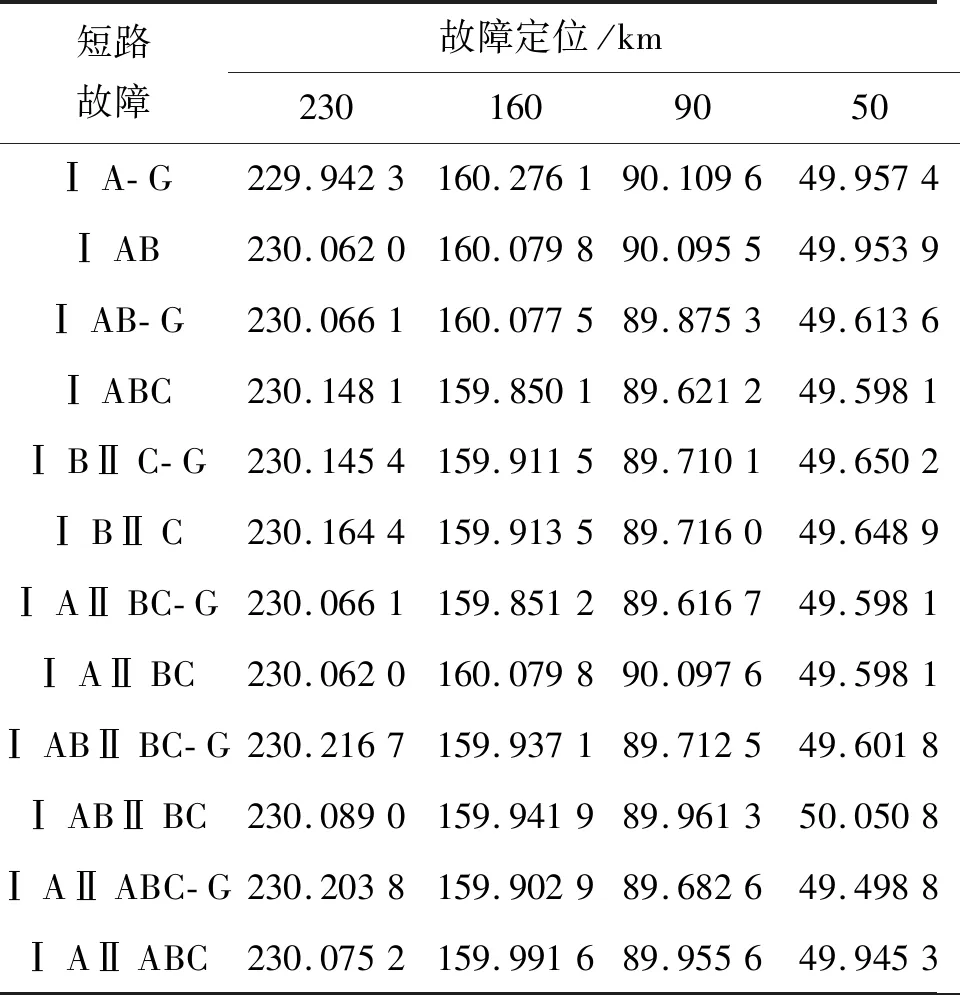
表3 不同短路故障情况下故障定位结果Tab.3 Location results of different faults

同塔双回线经不同过渡电阻(过渡电阻分别取0 Ω、50 Ω、100 Ω、300 Ω)发生短路故障时的仿真结果如表4所示。由表4可知，同塔双回线在发生不同短路故障情况下，该算法无论过渡电阻大小，故障定位结果均可取得较高精度，可避免过渡电阻的影响。

表5列出了Ⅰ回线发生单相接地短路故障时，数据不同步的故障定位结果。其中过渡电阻设为50 Ω，不同步角设为-π/3、-π/6、0、π/6、π/3。由表5可知，故障定位结果不受不同步角的影响。

表5 数据不同步对故障定位结果的影响Tab.5 Effect of fault location on different non-synchronous angles

4 结 语

同塔双回线存在相间和线间耦合，因此在进行故障定位前需要对六相系统进行解耦计算，本文结合均匀换位线路的相模变换矩阵的数学性质，根据三相系统和六相系统之间的关系，推导出了能够适用于同塔双回线的新相模变换矩阵。该矩阵可用单一模量反映各种短路故障类型，且运算因子均为实数，实数运算相对简单，并且可减少计算量。ATP-EMTP仿真结果表明，将新相模变换矩阵用于同塔双回线的故障定位中，故障定位结果不受故障类型、过渡电阻和数据不同步的影响。