降低SRM转矩脉动的离线转矩分配函数研究

黄朝志 王 涛 屈资喻 刘细平

(江西理工大学电气工程与自动化学院 江西 赣州 341000)

0 引 言

开关磁阻电机由于其结构简单、成本较低、性能好等一系列优点，自问世以来受到国内外科研学者的广泛关注[1]。但是由于其固有的双凸极结构和非线性系统，导致其转矩脉动要比其他传动系统严重。此外，SRM的转矩脉动不仅是其噪声和振动的来源，也是电机驱动器上的扰动源[2]。

通常来说，抑制转矩脉动的方法主要包括优化电机的本体结构参数[3]和采用高级控制策略，如直接转矩控制[4]、自适应控制[5]和转矩分配函数控制(Torque Sharing Function, TSF)[6-8]等。离线转矩函数控制大多是在传统TSF的基础上采用两个以下的优化目标。文献[5]运用Tikhonov因子与转矩分配函数相结合，得出以铜耗和电流变化率为目标的优化函数，有效降低了转矩脉动和电流峰值，但由于其引入较宽的负转矩产生区域从而降低了电机的运行效率。文献[9]验证了导通角和重叠角对SRM的最大速度、铜耗和效率的显著影响，此外通过遗传算法对传统四种转矩分配函数的导通角和重叠角进行优化，降低了转矩脉动。文献[10]提出了一种新型的将转矩波形转化为电流波形的ik(θ,Tk)解析表达式，通过改变表达式中的参数对磁链变化率和铜耗进行比较，从中选择拓展速度范围或降低铜耗的转矩分配函数。

本文提出了一种在宽速范围内降低SRM转矩脉动的离线转矩分配控制方案。由SRM的电感-转矩特性，通过可逆转矩函数模型提出的两个关于转子位置的函数，将参考转矩转化为参考电流以实现良好的跟踪特性。将电流的平方(铜耗)和磁链变化率与Tikhonov因子相结合构造目标优化函数，通过效率和转矩速度性能之间的平衡选择，运用遗传算法进行优化，得出特定Tikhonov因子的离线转矩分配函数曲线。通过场路耦合仿真验证，与传统的线型、立方型转矩分配控制相比，本文提出的离线转矩分配控制策略能有效提升转矩-速度性能，降低转矩脉动。

1 转矩分配控制策略

1.1 SRM的电感模型分析

由于开关磁阻电机的双凸极定转子结构以及互磁易饱和的特点，大多数SRM的建模分析的基本目的是找出磁链、转子位置角和相电流之间的关系。如果电流ik和位置角θ被选定为独立变量，那么磁链ψk通常被定义为：

ψk(θ,ik)=Lk(θ,ik)ik

(1)

式中：Lk表示为相电感。但事实上电感Lk不仅和相电流ik有关，也与转子位置角θ有关。对于所研究的12/8极开关磁阻电机，借助Maxwell-19.3软件进行有限元分析，定子外径120 mm，定子内径69.6 mm，铁芯材料DW360-50，电机功率1.2 kW。通过有限元分析，得到在相电流分别为1、2、3、4、5、6、7、10 A时，相电感Lk在不同转子位置角θ下的值，如图1所示。

图1 SRM的电感曲线

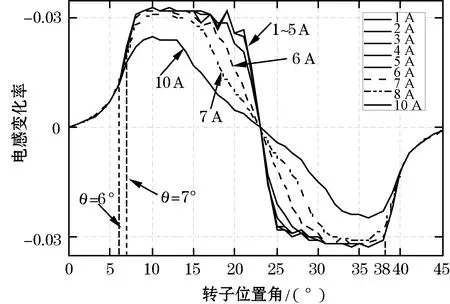
图2 电感相对于转子位置的变化率曲线

由式(1)可知，电感L取决于电流ik和位置角θ。当磁链不饱和时，SRM在小电流下的电感L主要受位置角θ的影响，结合式(1)可得：

(2)

式中：Tk(θ,ik)为导通相的相转矩；Wc(θ,ik)为绕组的磁功能；电感值L关于θ的微分函数值的2倍定义为Lp(θ)。

1.2 SRM的转矩控制

图3所示为基于TSF实现三相SRM驱动的转矩控制原理图。将速度环输出的总参考转矩Te-ref根据转子位置角θ划分为各阶段的单相参考转矩Tk-ref。通过T-θ-i，即“转矩-位置-电流”模块把单相参考转矩值转换为参考电流ik-ref，与实际相电流ik比较后，经过滞环比较器进行调节控制。

图3 基于转矩分配函数的SRM控制系统框图

为了最大限度降低转矩脉动，常用的转矩分配函数通常选择线型、正弦函数型、指数型或立方型。在换相过程中，每相的参考转矩Tk-ref的函数被定义为：

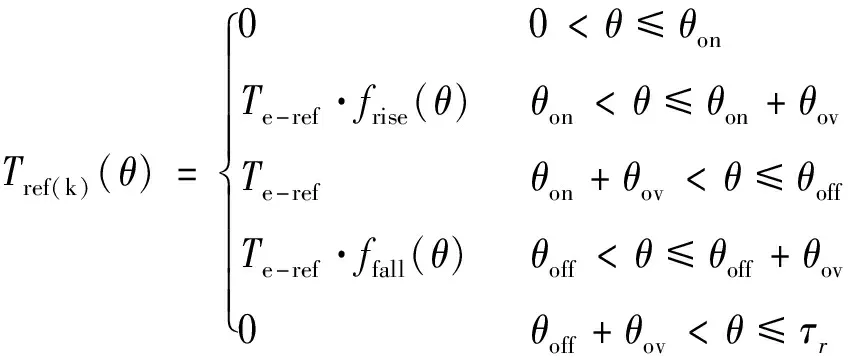
(3)

θoff=θon+ε

(4)

(5)

1.3 TSF的评估指标

为了评估转矩分配函数的转矩-速度性能、SRM的效率和转矩脉动率，定义如下判定指标。

1)转子位置的磁链变化率。磁链相对于转子位置的变化率(ARCFL)是评估SRM的转矩-性能的一个重要标准，其值Qψ的表达式如下：

(6)

式中：ψrise为导通相第k相得上升磁链；ψfall为前一相第k-1相的下降磁链。

不考虑磁链耦合和相位压降的情况下，可由SRM的电压公式推导出公式如下：

(7)

(8)

2)铜耗。铜耗是影响电机效率的重要因素之一。铜耗可以用电流在导通期间的均方根值，即用有效值Irms来表示：

(9)

3)转矩脉动率。与式(11)的分析方法类似，本文定义一种计算瞬时转矩脉动平均值的方法如下：

(10)

1.4 可逆转矩函数模型

(11)

式中：Lp(θ)已知；g(θ)也是关于转子位置的函数：

(12)

(13)

在不同转子位置θ和电流ik下，通过式(13)计算的参考转矩值与Maxwell有限元仿真得到的参考转矩拟合曲线如图4所示。可以看出，该可逆转矩函数的拟合度较高，同时适用于线性磁链区域和饱和磁链区域。

图4 有限元仿真的参考转矩曲线

2 基于遗传算法优化的TSF

2.1 基于Tikhonov因子目标函数

由式(8)可知，为了最大限度地提升SRM的宽速范围，应最小化磁链变化率的值。因此本文采用以参考电流及其微分值的平方与Tikhonov因子相结合的方法构造新型目标函数如下：

(14)

s.t. 0≤ik-1≤Imax;0≤ik≤Imax

Tk-1(θ,ik-1)+Tk(θ,ik)=Te

式中：m、n、p、q为Tikhonov因子；ik-1(θ)、ik(θ)表示当前转子位置角θ下前一相与后一相的电流值；电流变化步长和位置变化步长为Δik=ik(θ)-ik(θ0)，Δθ=θ-θ0，θ0表示前一时刻的转子位置角，ik-1(θ0)、ik(θ0)为该时刻相邻两相的电流值。

为了解决式(14)中的优化问题，需要确定Tikhonov因子m、n、p、q的值。Tikhonov因子的大小表明该目标函数的重要性，其值越大则对结果的影响也就越大。为了简化分析，以避免复杂的公式推导，将当前相的参考电流作为基准值，即令d=1；然后考虑在导通和关断阶段，磁链变化率对电流有效值，即铜耗的影响程度，定义如下：

(15)

事实上，导通角和关断角的取值都会对磁链的变化率产生重要影响[9]。经过在不同θon、θoff和θov下，直线型和立方型TSF的仿真比较得知，线型TSF的磁链变化率大于立方型TSF。以θon、θoff和θov分别为4.5°、19.5°和3°，负载转矩为1 Nm为例，图5给出了参考转矩以及磁链变化率的曲线波形。

图5 参考转矩、磁链和磁链变化率曲线

J=r(ik(θ)2+sik-1(θ)2)

(16)

式中：r可以调整，以平衡铜耗损失和转矩脉动率。由图(2)可知，在导通初始阶段，电感变化率较小，因此需要更高的相电流以达到参考转矩值。r值较小时强调转矩脉动率，k-1相的电流有效值Irms会增大，且转子达到对其位置后剩余的磁共能就会产生负转矩而降低电机的效率；而r值增大时，则强调铜损耗，k相电流值增大导致转矩脉动率的上升。设定r取值范围为0.25～1时的优化效果如图6所示，从上到下的曲线簇中，各曲线r的取值分别为1、0.75、0.5和0.25。

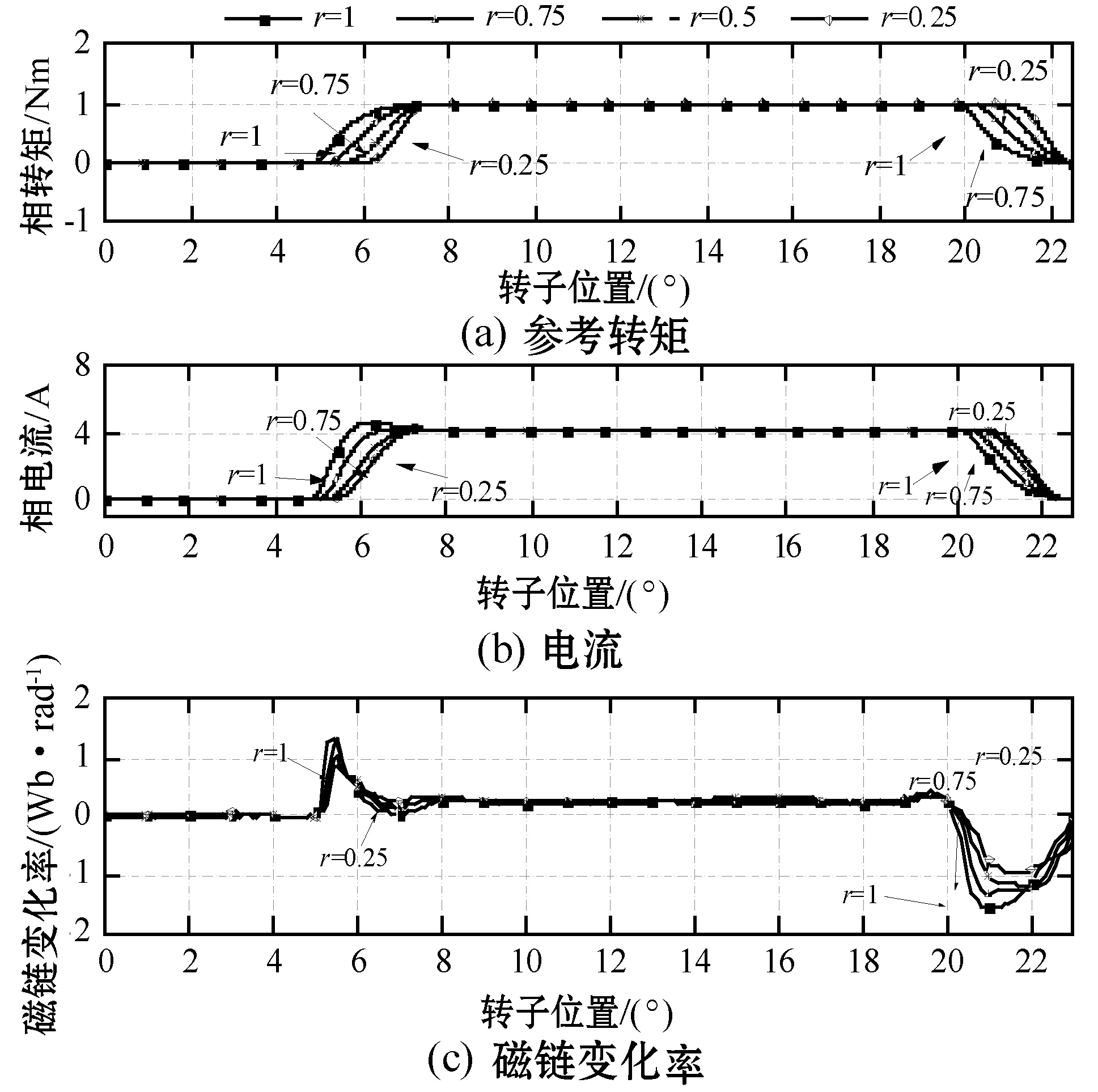
图6 不同Tikhonov因子下的优化效果

当r=1时，这与传统TSF的控制效果类似，在每一相导通初期，相电流ik急剧上升并产生峰值。r取值越小，导通初期被分配的转矩越小，关断阶段被分配的转矩也就越大，进而控制了导通初期和关断阶段的瞬时电流变化率。

由图5和图6可知，在SRM整个运行阶段，关断阶段的磁链变化率的绝对值是最大的，根据式(8)，最大TRFS也就由关断阶段的磁链变化率决定。在参考转矩为1 Nm时，直线型、立方型及r取0.5时优化TSF的最大磁链变化率分别为12.6、6.4 和1.2 Wb/rad，可得最大TRFS为17.5、31.3和166.7 rad/s，因此直线型、立方型的最大TRFS为167.1、298.9 r/min，而优化TSF在r=0.5时的TRFS可达到1 591.9 r/min，明显提高了SRM的速度性能。

该算法可应用于任何SRM的设计，以获得更好的转矩脉动性能。在宽速范围内，可以调整式(16)中的r值以增加选择的灵活性。通过选择合适的Tikhonov因子可以增加重叠区域，减小电流变化率，如图5所示。优化后的TSF比传统TSF的磁链(电流)变化要平稳得多，最大磁链变化也明显降低了。

2.2 遗传算法

随着转速的升高，由于励磁周期的缩短以及感应电压的影响，选择合适的r值以实现保持最小铜耗和减少转矩脉动率的平衡愈发困难。遗传算法(Genetic Algorithm，GA)是借鉴遗传进化和自然选择的思想和发展机制的一种直接搜索算法，它从随机创造种群开始，通过不断重复地评估、选择、交叉和突变，直到达到预定的世代数或者找到满意的解决方案[12-13]。因此，对于单目标优化参数的式(16)来说，遗传算法可以得到更精确的r值。

在执行基于GA的算法之前，需要进行适当的编码，根据搜索范围，设置精度为e-4，得到10位数的二进制编码。种群大小和迭代次数都设为50，如果后代的输出参数的值不符合约束范围0～1，则抛弃该数值。由于目标函数是求相电流平方以及电流相对于转子位置倒数平方的最小值，因此定义适应度函数如下：

(17)

式中：Xi表示种群中第i个个体，其自适应函数值越大，表明个体的适应度越好。

选择操作采用轮盘赌[13]选择法，其目的是产生更多的后代，通过个体的适应度值与种群的总适应度值之比来计算个体i能遗传到下一代的概率：

(18)

式中：F(Xi)、P(Xi)和N表示为个体的适应度值、被选择的概率和种群的大小。F(Xi)值越大，则繁衍出下一代的概率也就越高。

交叉的目的在于将不同个体的有用片段重新组合，形成适应度更好的后代。交叉点的位置和个数由算法随机生成，以便克服局部最优现象，其原理如图7所示。

图7 交叉操作原理图

突变操作是另一种避免局部最优的方法。原理是以较小的概率随机改变个体中的每位基因的数值，突变的示例结果如图8所示。

图8 突变操作原理图

3 仿真结果

对于该12/8极三相开关磁阻电机，直流端电压Ud为220 V，给定转矩为2 Nm，采用AnsysEM 2019R1套件中的Maxwell与Simplorer的耦合场路仿真平台，确保瞬态有限元分析和驱动系统的仿真分析实时、同步，以验证所提出离线TSF的性能。电流滞环宽度设为0.1 A，仿真采样时间ts为1 μs。每个权重参数r值由遗传算法确定，以确保最优选择，主电路模型拓扑如图9所示。

图9 场路耦合仿真主电路拓扑图

图10为未采用遗传算法下，不同Tikhonov因子的优化TSF与传统直线型和立方型TSF的转矩脉动率和电流有效值的对比结果。

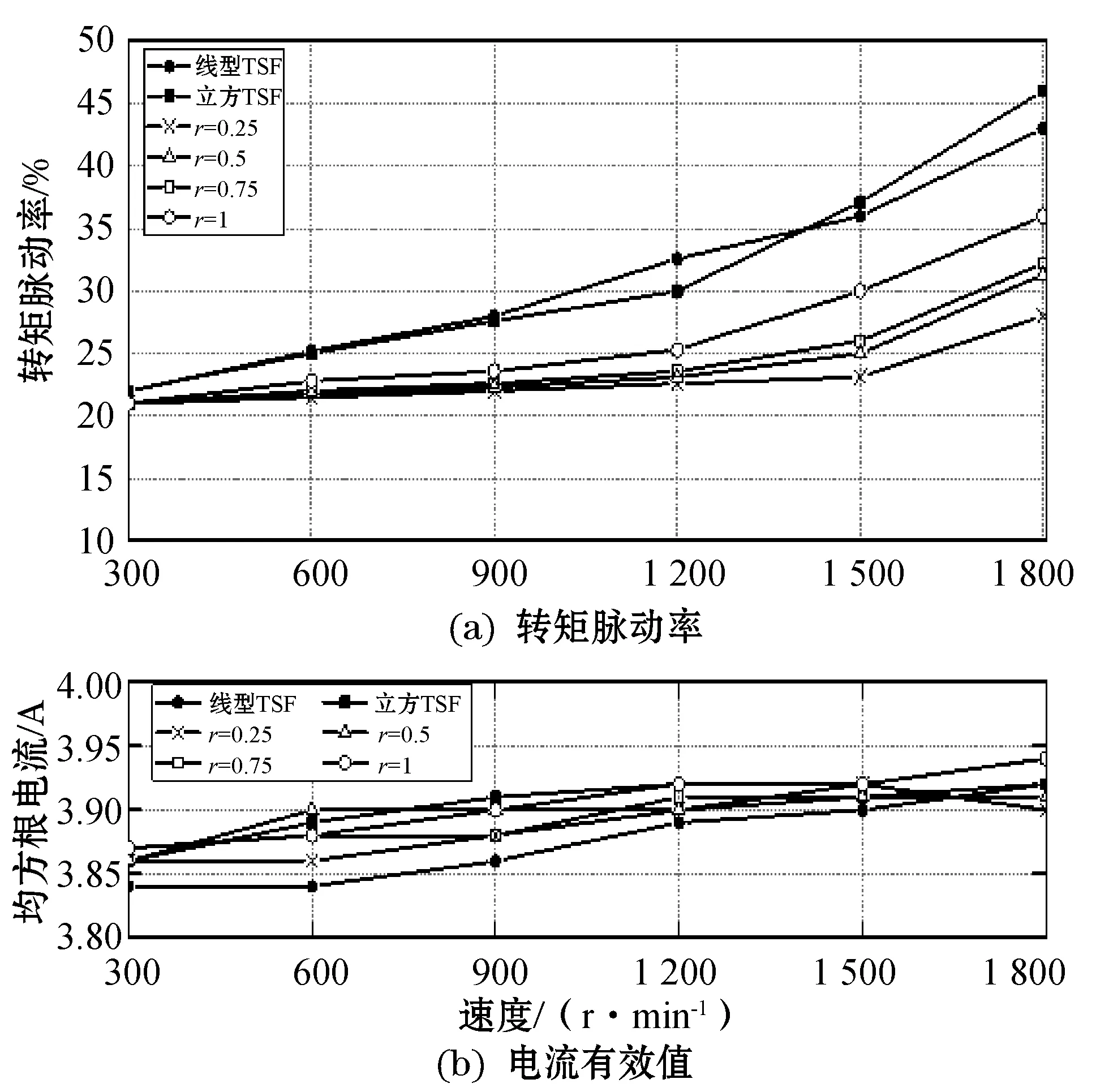
图10 不同TSF下的对比结果

图10(a)和(b)比较了在2 Nm转矩下，不同转矩分配函数的转矩脉动率Tripple和电流有效值Irms，此时导通角θon和重叠角θov设定为4°和3.5°。电机转速高于ωmax后，在转子到达下一个对齐位置时，励磁电流并不能减小到零，因此相转矩Tk-ref会产生一定的负转矩，从而导致了转矩脉动。随着转速的进一步提高，换向时间减小，参考转矩跟踪实际转矩的能力降低，转矩脉动变得更加明显。传统的线型和立方型TSF在1 800 r/min时的转矩脉动率几乎是300 r/min时的两倍；而在1 800 r/min下，当Tikhonov因子r小于0.75时，离线TSF的转矩脉动率要小得多，r=0.25时的转矩脉动率最低。由图10(b)可知，离线TSF和线型以及立方TSF表现出了相似的电流平均值，r=0.5的电流平均值Irms最小。通过综合考虑最大无转动脉动速度、铜耗以及转矩脉动率可得知，选取r=0.5的离线TSF是一种低转矩脉动、低铜耗的开关磁阻电机控制策略。

为验证本文所提出的采用遗传算法后优化离线转矩分配函数的有效性，分别在600、1 200、1 800 r/min下进行对比实验。为了使离线TSF和传统TSF进行公平比较，还可以根据铜耗最小化的基础上选择导通角、重叠角和关断角[5]，依据文献[7]方法选择θon、θov分别为3.3°、4.2°。

在转速为600 r/min、负载转矩为2 Nm时，采用常规的直线型、立方型和本文所提出的离线转矩分配函数控制得到的相电流、相转矩和相参考转矩以及总转矩如图11所示。

图11 转速为600 r/min，转矩为2 Nm,θon=3.3°，θov=4.2°的仿真结果

在转速为1 200 r/min、负载转矩为2 Nm时，采用常规的直线型、立方型和本文所提出的离线转矩分配函数控制得到的相电流、相转矩和其参考转矩以及总转矩如图12所示。

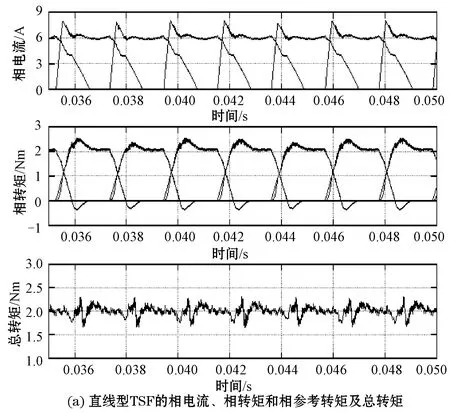
图12 转速为1 200 r.min，转矩为2 Nm,θon=3.3°,θov=4.2°的仿真结果

在转速为1 800 r/min、负载转矩为2 Nm时，采用常规的直线型、立方型和本文所提出的离线转矩分配函数控制得到的相电流、相转矩和其参考转矩以及总转矩如图13所示。

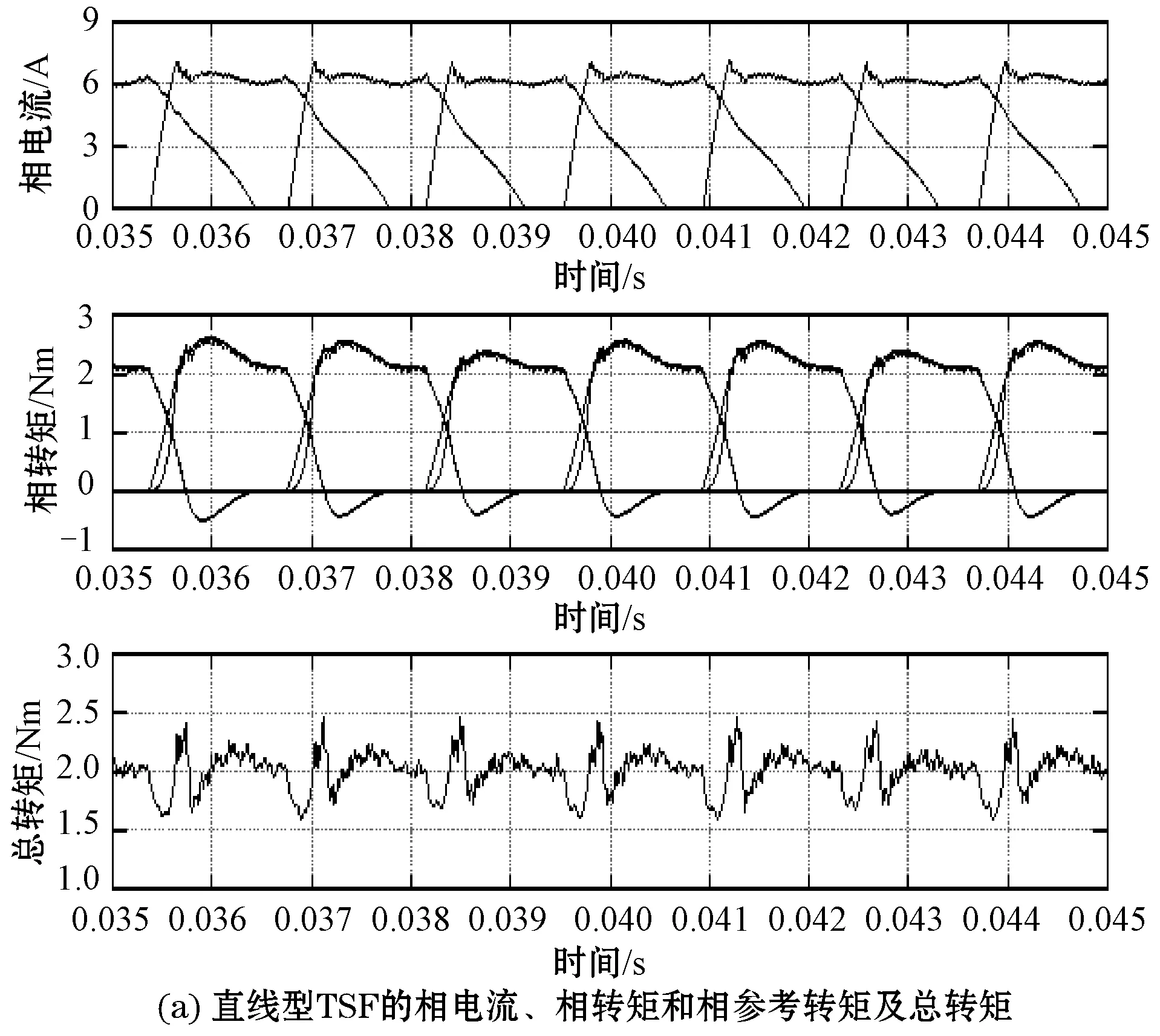
图13 转速为1 800 r/min，转矩为2 Nm,θon=3.3°,θov=4.2°的仿真结果

在上述三种转速下，采用直线型、立方型以及离线转矩分配函数控制时，SR电机性能对比如表1所示。

表1 不同转速下直线型、立方型和离线TSF性能对比

由图11-图13可知，在负载转矩为2 Nm时，本文所提出的离线转矩分配函数控制策略能有效降低转矩脉动率，且相电流的峰值Imax均小于传统线型和立方型转矩分配函数控制。在600和1 200 r/min下，相对于线型和立方型TSF，离线TSF的相转矩跟踪特性较好，跟踪误差接近于零；当电机转速超过ωmax而达到1 800 r/min时，离线TSF的跟踪特性变差，跟踪误差开始增大，此时转矩脉动率为31.42%，但相对于传统的线型TSF和立方型TSF，该控制方式仍表现出显著的优越性。

4 结 语

本文提出一种高效的离线TSF来降低开关磁阻电机的转矩脉动。引入Tikhonov因子来实现离线转矩分配函数的优化，优化目标包括最小化铜耗Irms和最大化转矩脉动速度ωmax。针对1.2 kW 12/8极开关磁阻电机进行耦合场路仿真分析，通过可逆转矩函数模块将相参考转矩转化为相参考电流，从而避免在换相区间出现相电流峰值较大的情况。与传统线型、立方型转矩分配控制策略相比，该策略在提升转矩-速度性能方面具有优势，增加到了近1 800 r/min，分别是线型和立方型转矩分配控制策略的10倍和5倍多。在降低转矩脉动率和提升电机运行效率方面，采用遗传算法在不同转速下选择合适的Tikhonov因子数值，使离线转矩分配函数和线型及立方型转矩分配函数具有相当的铜耗，且显著降低了转矩脉动率。