基于SPARK的大规模RDF数据上的SPARQL查询算法
2020-12-14崔家奇
崔家奇 闫 威
(辽宁大学信息学院 辽宁 沈阳 110036)
0 引 言
资源描述框架(RDF)[1]是W3C提出的一种描述网络资源的知识模型,用来表示Web中已识别的信息,利用图模型来表示资源关系。随着RDF数据的迅速增加,SPARQL[2]成为RDF数据的主要查询语言。早期对RDF数据的管理主要是通过集中式系统[3-4]。随着RDF数据集规模迅速扩大,单台机器很难高效地存储和查询大规模RDF数据,因此需要使用分布式环境来提高查询性能。
近年来,研究者们对分布式平台上实现RDF数据的处理做了大量的研究[5-7]。其中一种基于云计算平台的分布式RDF数据管理方法,利用现有的分布式计算平台(Hadoop,Spark,Trinity)存储数据以及执行SPARQL查询,具有良好的可扩展性和容错性。基于Hadoop平台的主要缺点是必须将中间结果写到磁盘,降低了查询性能,因此基于Spark的RDF存储查询受到学者关注,产生了大量的研究成果[8-13]。S2RDF[10]是一种扩展垂直分区(ExtVP)的RDF数据关系分区技术,扩展了垂直分区方法以排除不必要的数据。S2RDF并不直接在Spark上运行,它将Spark查询转化为SQL,然后在SparkSQL上执行。SPARQLGX[11]将数据集垂直分区,三元组(s,p,o)存储在名为p的文件中,其内容仅保留s和o。在查询转阶段将三重模式转换成可执行的Spark代码,并通过优化查询的连接顺序来提高查询效率。S2X[12]和P-Spar(k)ql[13]利用Spark 图分析工具Graphx来回答查询。S2X的优点是利用图形并行和数据并行技术,但会产生大量的中间结果。P-Spar(k)ql通过图的一些基本信息来更改SPARQL查询的顺序优化查询。这些方法的总体目标都是通过利用数据并行化来提高查询性能。但它们大都采用简单的分区技术(垂直或散列分区),忽略了数据分区是高效查询处理的关键性因素,影响了查询应答的效率。
另一种基于数据划分的分布式RDF数据管理方法[14-19]为了减少查询处理期间的通信代价将RDF数据集进行划分,使它们分别存储在不同的节点上。同时每个计算节点都安装单机的RDF数据管理系统,例如RDF-3X[3]、gStore[4]。然后将查询图进行划分,每个节点并行执行子查询,最后将子结果进行连接和合并得到最终解。这种方法可以有效地降低通信,加快查询速度,但在数据划分时可能会导致大量的冗余。典型的数据划分方法是散列分区,它按照三元组主语或宾语的散列值将三元组进行划分,将具有相同主语或宾语的三元组划分到同一个计算节点上,被广泛用于很多分布式RDF查询引擎[14-15]。散列分区使得星形查询非常容易,可以在单个分区内完成星形查询,不需要节点间的通信,且没有产生三元组的复制,但并不适用于复杂查询。H-RDF-3X[16]和SHAPE[17]在划分顶点后实现n-hop,通过复制三元组来降低节点间的通信成本,并且在执行半径小于等于n的查询时可以完全并行执行,而无须任何额外的通信。这两种方法的缺点在于不能保证将顶点均匀地划分到各分区中。文献[18]在考虑RDF数据图结构的同时也考虑了查询图结构,提出一种端到端路径的划分方法,执行复杂查询时能够减少查询分解的子查询数量,并通过顶点合并来减少数据冗余。文献[19]将模式相似的实体进行聚类,在保持RDF数据语义结构的同时,也确保了各节点之间的负载均衡,并在此基础上对查询进行优化。该方法能够有效地提高查询效率,但当中间结果比较大时,需要耗费大量的通信代价。这些方法都基于Apache Hadoop上实现,查询效率受到磁盘的读取和写入限制。
本文提出一种基于Apache Spark的SPARQL查询方法。本文主要工作如下:
1)提出一种平衡的语义划分方法,在将顶点按照URL层次结构划分的同时考虑各分区负载的均衡性,生成n-hop语义平衡分区。
2)在查询阶段将查询图进行有效的分解,并优化查询连接来减少匹配次数,提高查询效率。
3)在Spark集群上使用合成数据集LUBM进行实验,并与流行方法进行比较。实验结果表明,本文方法能够实现分区间的负载均衡,减少分区通信,加快查询速度。
1 基本概念
定义1RDF数据图。U、B和L(URIs、空白节点和文本信息)为任意不相交的集合,三元组(s,p,o)=(U∪B)×U×(U∪B∪L)。其中:s为主语(subject),表示现实世界的一个实体;o为宾语(object),表示一个实体或者一种概念(例如性别,家庭住址等);p为谓语(predicate),表示主语和宾语之间的关系。一个或多个三元组构成了RDF图,实体表示图中的顶点,谓词表示边。图1为RDF数据图示例。

图1 RDF数据图
定义2SPARQL查询。SPARQL是一种查询和检索RDF数据的查询标准语言。查询部分包括四种类型:SELECT, CONSTRUCT, ASK, DESCRIBE。SELECT是最常用的查询,用于返回满足设定条件的值。FROM限制数据的来源,WHERE定义包括变量的三元组模式,类似于RDF三元组结构,主语、谓语和宾语可以部分或全部替换为变量。图2为SPARQL查询图。

图2 SPARQL查询图Q2
定义3星形结构。给定RDF图G=(V,E,L)。星形结构表示为S=(VS,ES,LS),且VS={v}∪{vi|vi∈V,(v,vi)∈ES,1≤i≤|ES|}。LS是一组星形结构的标签。
Apache Spark是一个专为大规模数据处理而设计的一种基于内存计算的分布式计算平台。由于Spark基于内存计算,因此比Hadoop(基于磁盘)的计算效率更高。RDD(弹性分布式数据集)是Spark中最核心的概念,是一个分布式的、具有容错机制的、不可变的数据集,主要包含Transformation和Action两种类型的操作。RDD具有血统特点,当前RDD与其父RDD具有依赖关系,多个RDD之间形成有向无环图DAG,因此具有高效率和容错性。
2 基于散列的数据划分方法
2.1 n-hop扩展星形结构
散列分区是按照主语的哈希值将三元组划分,生成平衡的分区,保证星形查询能在单个分区内完成。但对于如图2所示的复杂查询,在执行查询时会将查询图Q2分解成三个星形结构子查询,每个查询子查询会在单个分区内执行,但在子查询执行完毕,将子查询进行join时,会产生大量分区间通信代价,降低查询速度。为了降低分区间的通信代价,本文实现n-hop扩展星形结构来确保n跳范围内的查询可以并行执行。
1-hop扩展星形结构等同于星形结构,表示分区内的每一个顶点v,通过有向边连接的距离为1的顶点,将这组顶点与原始顶点以及它们的边添加到分区中,如图3(a)所示。2-hop扩展星形结构表示从1-hop扩展星形结构中的宾语开始,添加它们的1-hop扩展星形结构,如图3(b)所示。

图3 GraduateStudent20的扩展星形结构
n-hop扩展星形结构可以保证n跳范围内的查询可以并行执行。用2-hop后,Q2的结果可以在单个分区的内获得,无须分区间的通信。n越大,复制的三元组数目越多,占用的存储空间越大。实验表明,大多数查询都可以在2-hop扩展星形结构内完成。本文使用Spark API实现2-hop扩展星形结构,通过每个三元组的主语对其添加散列值,得到顶点的星形结构fileRDD:
val fileRDD=sc.textFile(″data.ttl″).map(x=>x.split(″ ″))
.map(t=>(t(0),t(1),(t2)))
.map(case(s,p,o)=>(s.hashCode,(s,p,o)))
之后在fileRDD的基础上再次进行1-hop扩展得到2-hop扩展星形结构towHopRDD:
val twoHopRDD=fileRDD.map({case(k,(s,p,o))=>(o,(k,p,s))})
.join(fileRDD.map({case(k,(s1,p1,o1))=>(s1,(p1,o1))}))
.map({case(s1,((k,p,s),(p1,o1)))=>((k,(s,p,s1),(s1,p1,o1)))})
.filter({case((k,(s,p,o),(s1,p1,o1)))=>s!=s1})
.map({case(k,(s,p,o),(s1,p1,o1))=>(k,(s1,p1,o1))})
.union(fileRDD).distinct()
获取星形结构并将其扩展为2-hop结构之后,将所有三元组划分到不同的分区。在根据主语对每个三元组添加散列值之前,需要考虑两个问题:1)负载均衡;2)顶点复制。数据倾斜会增加某些分区的工作负担,严重影响查询的效率。另外,顶点可能存在多个2-hop星形结构中,将具有许多公共顶点的2-hop星形结构划分到同一个分区中,能够有效地减少三元组的复制,节省存储空间并减少三重模式的搜索空间,提高查询效率。
2.2 顶点分区
文献[11]认为URI引用通常具有路径层次结构,将具有共同祖先的URI放在同一个分区,可以显著减少三元组的复制量。URL的典型层次结构为“http://domainname/path1/..../pathN#fragmentId”,例如“http://www.Department17.University18.edu/FullProfessor1/Publication5”,可以获得该URL的层次结构为edu,Unuversity,Department,FullProfessor,Publication。在层次结构的任何级别,如果共享此层次结构的不同URL的数量大于或等于分区的数量,则用从顶部到所选级别的层次结构而不是完整的URL来进行散列划分。但当选定的层次结构的种类与分区数目相差不是非常大时可能会产生严重的负载不均衡。本节在三元组层次结构划分的基础上,通过限制每个分区的实体数目来实现各分区的负载均衡。
假设每个分区中当前实体的数量为NR,当NR≥δ时,不再往分区内划分实体,δ为分区的数量阈值,通常设置为:
(1)
式中:NE为数据集中实体总数;NP为集群中分区个数。
先根据选定的层次结构将顶点进行分组,将每组顶点进行哈希聚类。然后按照分组依次将实体划分到相应分区中,如果当前分区中的实体数目大于等于δ,则停止划分。如图4(a)所示,此时分区一和分区二中的实体数目已经达到了阈值。第一次划分之后,将未划分顶点按照分组划分到未达到阈值的分区中。将u9中未划分的实体划分到未达到阈值的分区三中,再将u10中未划分的实体划分到未达到阈值的分区三中。当分区三达到阈值后,将u10中剩余实体划分到未达到阈值的分区四中,如图4(b)所示。在实体划分之后实现2跳扩展星形结构,将划分后的数据集存储在twoHopRDD中。

图4 数据划分与分布
3 查询处理与优化
3.1 查询分解
执行查询操作前,需要把查询图Q分解成若干个子查询Qi。每个查询图有多种划分方法,为减少子查询连接的通信代价,本文使划分的子查询数目最少。查询图Q有两种划分方法可以使得查询图仅有两种子查询,如图5所示。

图5 查询图分解
为减少子查询连接操作的代价,需令两个子查询的结果数量乘积最小,即min(Num(Q1)×Num(Q2))。由于无法直接获取每个子查询的结果数量,本文最大化各子查询三重模式个数的乘积φ来确定选择的查询分解方式:
(2)
式中:n为分解的子查询个数;|Qi|为子查询中三重模式的个数。图5(b)中的子查询三重模式的乘积φ=3×1=3,图5(c)中的子查询三重模式的乘积φ=2×2=4,因此本文选择图5(c)的分解模式。
3.2 查询执行
每个子查询Qi需要在每个分区内进行,得到子查询结果之后,各子查询间需要进行join连接,最终得到查询图Q在数据图中的查询结果。
利用filter算子实现三重模式查询,需要遍历每个分区内所有三元组数据。目前大多数查询都是在已知谓词的情况下查询,因此为了减小查询的搜索空间,本文创建了谓词索引。通过谓词来查询结果时,可以迅速定位搜索区间。谓词索引表如表1所示。

表1 谓词索引表
如图6所示,散列划分将Q2分解成三个子查询,但SSQ在分区内即可完成查询。在执行子查询Qi时,使用mapPartition算子对twoHopRDD中的每个分区进行操作。通过filter对每个三重模式进行查询,将Qi中的三重模式查询结果在分区内进行连接,避免了分区之间的通信,提高查询效率。此外,对三重模式的查询结果使用groupBy进行分组,能够有效地减少连接次数,减少查询时间。

图6 Q2查询执行图
三重模式连接在SPARQL查询过程中执行代价最高,子查询内和子查询间的存在多种连接顺序,不同的连接顺序很大程度上决定了SPARQL的查询效率。当对子查询Qi中n个三重模式进行连接时,需要进行n-1次分区内连接操作来得到子查询结果。不同的三重模式查询连接顺序产生不同的中间结果,中间结果的大小很大程度上影响查询的效率。因此,本文提出了一种基于贪心选择的优化连接方法来优化查询。
1)通过filter对子查询内所有三重模式进行查询得到结果子句集SQi={Qi1,Qi2,…,Qin};
2)贪心选择查询相邻的三重模式且子句集大小乘积最小的两个子句集进行连接,得到新的子句集Qi(n+1);
3)更新查询结果SQi。删除连接完成的子句集并添加新的查询子句集;
4)重复步骤2)和步骤3),直到SQi中子句集的个数为1,输出查询结果。
得到各子查询后,将子查询按照同样的连接顺序进行join连接得到最终查询结果。
4 实 验
4.1 实验环境
实验在具有5个节点的集群上进行,包含4个worker节点和1个master节点。每一个节点的CPU为双核1.9 GHz,内存为8 GB,操作系统为CentOS7,集群环境为基于Hadoop 2.6.5上构建的Spark 2.3.0,Scala的版本为2.11.0,RDF数据被存储在HDFS中。
实验数据集选用目前最为常用的测试数据集LUBM。LUBM是一个以大学为本体的合成数据集,通过改变相应的参数可以得到不同大小的数据集。本文使用LUBM生成器分别生成1、10、30、50个学校。
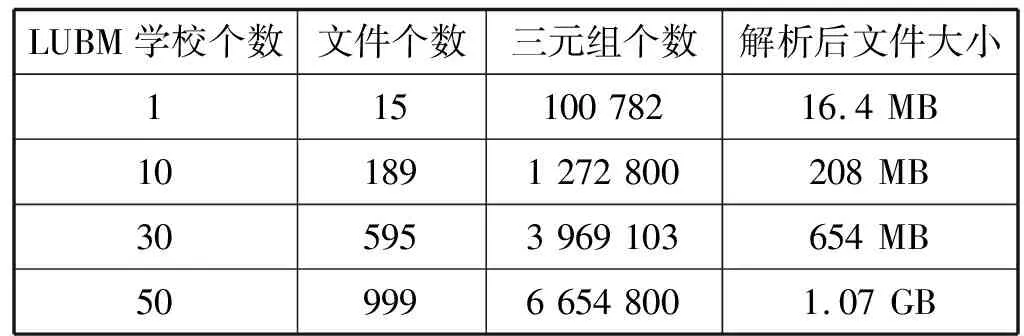
表2 LUBM数据集基本信息
4.2 性能比较
为了充分利用集群中worker节点的8个核心数,本文将数据集划分为8个分区。分别在LUBM1、LUBM10、LUBM30、LUBM50上比较基于主语的散列划分(Hash-s)[20]、主语散列2跳扩展星形结构(Hash-2f)、语义散列2跳扩展星形结构(SHAPE-2f)[17],以及本文基于语义平衡的2跳扩展星形结构(SSQ-2f)的分区均衡性以及数据冗余。使用SHAPE-2f和SSQ-2f划分数据时,选定从edu到department层次结构将LUBM1进行散列划分,edu到University层次结构将LUBM10、LUBM30、LUBM50进行散列划分,如表3所示。其中:max(σ)和min(σ)分别表示最大分区和最小分区中三元组的个数;Ratio(ζ)表示所有分区中的三元组数量与原始数据集中的三元组数量的比率。

表3 分布与冗余
可以看出,Hash-s和Hash-2f数据分布平衡,但Hash-2f划分数据后有大量三元组复制。Shape-2f将数据按照URL的部分层次结构进行散列划分,几乎没有任何三元组复制,但当共享该层次结构的URL的数量和分区数目相差不是很大时,会造成严重的分区间负载不均衡。本文方法在按URL部分层次结构划分的基础上进行再次划分,虽然会复制少量的三元组,但在具有不同学校数量的LUBM数据集下各分区的三元组数目都相对均衡。
4.3 查询评估
本节在LUBM30上比较Hash-s、Hash-2f、Shape-2f、SSQ-2f的查询性能。Shape-2f是基于Hadoop的分布式RDF数据管理系统,为了获得公平的实验结果,使用Scala API重写相关分区算法。本文使用LUBM提供的基准查询,将查询分为星形查询和复杂查询。不同查询的处理时间如图7所示。

图7 不同查询的处理时间
图7(a)显示了不同方法针对星形查询Q1、Q3、Q5、Q6、Q10的查询性能。可以看出,SSQ-2f与Hash-s对于星形查询效果最佳,因为星形查询可以在单个分区内并行执行,且两种划分方法分区划分均衡,仅有少数的复制量或没有任何复制。Hash-2f具有大量的三元组复制,Shape-2f划分后的分区不均衡,都导致查询的效率将低。
图7(b)显示了不同方法针对复杂查询Q2、Q7、Q8的查询性能。Hash-s在执行复杂查询时,需要将查询分为若干个子查询,涉及到分区间的通信。Hash-2f、Shape-2f以及SSQ-2f可以在单个分区(Q2,Q8)或两个分区(Q7)内执行查询,很大程度上减少了分区间的通信。SSQ-2f分布均衡,数据冗余小,并且对查询处理进行优化,因此对于复杂查询SSQ-2f效率最好。
4.4 可扩展性评估
本节使用Q1、Q2、Q7三个查询来验证SSQ-2f的可扩展性。分别改变LUBM数据集的大小以及分区个数来验证该方法的可扩展性,如图8所示。由图8(a)可见,随着数据集的增大,每个分区的工作量增加,查询时间呈线性递增。图8(b)表明随着分区数的增加,查询的并行度增加,Q1和Q2的执行效率不断提高。但由于Q7不能在单个分区内完成,因此各分区的通信开销也不断增加,导致Q7的执行时间先减少后增加。

图8 可扩展性验证
5 结 语
本文提出一个基于Spark的RDF数据划分方法SSQ,将SPARQL查询转化为Spark分布式平台计算框架上的RDD操作。该方法在散列分区的基础上复制必要的三元组来使得查询可以在单个分区或者少量的分区内并行执行,减少分区间的通信。利用URL的层次结构划分的基础上实现再划分,不仅降低了三元组的复制率,同时实现分区均衡。对查询进行划分,使每个子查询可以在单个分区执行,并优化子查询内和子查询间的连接顺序来减少匹配次数,提高查询的执行效率。实验结果表明,本文算法在查询效率上具有明显优势并且具有良好的可扩展性。
