复合肥配料中利润最大化模型

刘 琦 刘文静

（天津农学院，天津 300384）

1 引言

随着市场经济的不断深入和经济全球化的不断推进，化肥企业之间的竞争日趋激烈，化肥企业面临复杂多变的市场环境和科技进步的挑战，环境的多因素和多变性压力，决定了化肥企业生存与发展的复杂性。为使化肥企业在竞争中存活或立于不败之地，化肥企业必须研究在不同的外部环境和内部约束条件下，为实现经营目标而采取的生产计划和销售策略。化肥企业必须要制定最佳的生产方案，进行合理又高效的生产，对多变的原材料价格市场做出快速、有效、准确的反应，以期用最低的生产成本来获取最大的利润，实现效益的最大化。研究以化肥厂生产现状为前提，以党的十八届五中全会提出的“创新、协调、绿色、开放和共享发展的五大发展理念”为指导思想，依托最优化理论方法和Matlab、Lingo优化软件，分别构建以利润最大化为目标函数的优化模型，以便为化肥厂指定全面的采购和生产计划，为化肥厂决策的调整提供可靠依据，进而推动整个化肥产业的定量化、科技化发展，提高化肥产业在市场竞争中的生存能力。因此，适应市场需求，研究复合肥配料加工过程中，如何降低生产成本，提高生产利润，成为企业生存的关键所在。

2 问题的提出

某复合肥料有5种原料组成，其中氮肥有3种，磷肥有2种，5种原料的价格随月份的变化如表1：

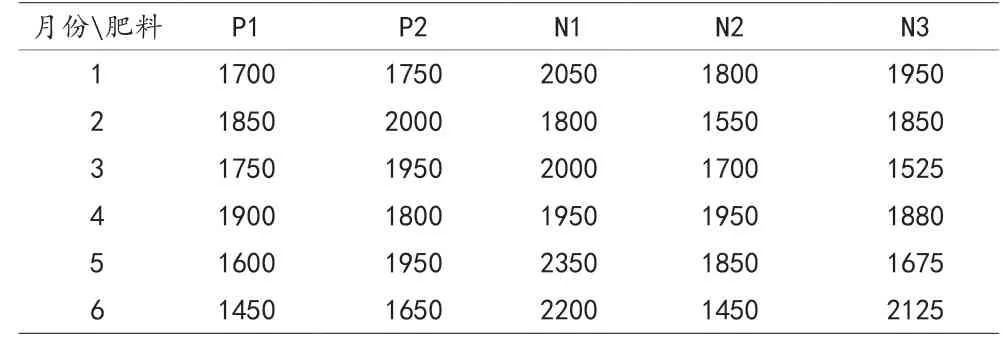
表1 半年内复合肥所需原料中所含成分及单价（元）

每个月最多可加工磷肥300吨，氮肥280吨.加工费用不考虑.复合肥售价为2550元/吨.每种原料最多可存储1200吨备用，存储费用为每月80元/吨.复合肥成品和加工过的原料不能存储.五种原料P1、P2、N1、N2、N3的杂质含量分别为6.5%，8.4%，1.5%，3.6%，5.2%，假设杂质是线性混合的.复合肥杂质指标为3%至7%个单位.

现有5种原料每种600吨，要求在6月底仍有这么多存货.采取怎样的采购和加工方案，化肥厂家能获得最大利润.

3 问题的假设与符号说明

3.1 问题的假设

1）假设每月加工的复合肥完全部出售；2）假设复合肥中的杂质是线性混合；3）加工过程中没有重量损失，且不计费用；4）将6个月看做一个整体建模.

3.2 符号说明

iij：第i个月第j种原料的采购量，mij：第i个月第j种原料的加工量.nij：第i个月第j种原料的存储量，qij：第i个月第j种原料的价格.i=1，2， …，6;j=1，2，…，5.

4 模型的建立和求解

复合肥配料中利润最大化模型如下：

使用Lingo软件求解该优化模型（用Matlab软件求解该线性规划模型，最优解相同.），得到目标函数的最大值是2651000元，最优采购和加工方案如表2（只显示非零项）：

表2 复合肥原料采购和加工方案

5 结论

该优化模型可推广到任一家复合肥生产加工企业，根据生产的产品不同，所使用原材料不同，修改表1中所需原料所含成分和单价，根据市场原料价格和企业生产、存储能力的相关要求修改相应的约束条件，仿照例子建立相应的利润最大化模型，使用Lingo软件或Matlab求解该优化模型，得到目标函数的最优解。使用该优化模型，需要掌握Lingo优化软件、Matlab软件部分知识，提高了使用者的门槛，下一步研究可将优化模型的建立和求解设置成程序，提升为软件APP，只需输入原材料信息，直接得到可视化的优化结果和，将大大方便用户或企业使用，便于推广。