高等数学中关于格林公式需注意的问题

季佳梁

（上海工程技术大学 数理与统计学院，上海 201620）

第二类曲线积分在物理上有广泛的应用．在高等数学和数学分析教学中，第二类曲线积分以及格林公式既是重点也是难点．正确地计算第二类平面曲线积分不仅是本科生必须熟练掌握的，也是全国硕士研究生入学考试中的重点内容．本文比较全面地归纳了应用格林公式求解第二类曲线积分时应该注意的问题．

应用格林公式求解第二类曲线积分时，首先应考察曲线积分是否满足格林公式的条件，即曲线是否封闭，能够围成一个闭区域；被积函数在该闭区域上是否存在一阶连续偏导数；曲线是否为闭区域的正向边界．若上述条件不满足，则需要用添辅助线等方法预处理，或者采用其他方法来计算曲线积分．

因此，首选考虑平面上曲线积分与路径无关以及格林公式来求解该问题．但题中所给曲线并没有围成封闭区域，所以必须添加辅助线使得曲线封闭．然而，此处若考虑不仔细，极易给出错误的过程与答案．

错解一：取C1:y=0，x:2→−2. 则

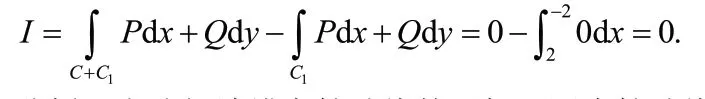
分析：上述解法错在辅助线的添加．因为辅助线包含点(0，0)，而被积函数P(x，y)和Q(x，y)在点(0，0)处无定义．因此，曲线积分无意义，后续计算也就没有意义了．

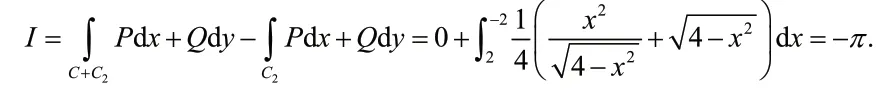
分析：上述解法还是错在辅助线的添加．因为使用格林公式时函数被积函数P(x，y)和Q(x，y)必须在C2与C所围区域D2上具有一阶连续偏导数[1]．本题中点(0，0)包含在区域D2内，P(x，y)和Q(x，y)在点(0，0)处无定义，故在点(0，0)处也不具有一阶连续偏导数．所以，不满足格林公式的使用条件．

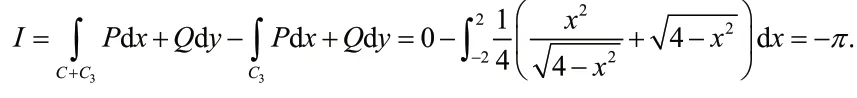
分析：在上述解法中，虽然C3与C所围区域D3中没有点(0，0)，且被积函数P(x，y)和Q(x，y)在区域D3上具有一阶连续偏导数，然而C3与C所构成的边界不是区域D3的正向边界，故不满足格林公式的应用 条件．

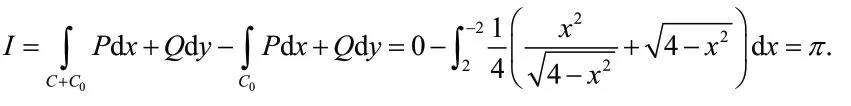
从上面的例子我们可以看到，应用格林公式时，被积函数P(x，y)和Q(x，y)必须在闭区域D上具有一阶连续偏导数．如果在区域D上含有奇点，那么要把奇点挖去，在挖去奇点的复连通区域上再应用格林公式，而挖奇点的一般原则是根据被积函数的特征来进行．

例2 已知f(x，y)连续，求曲线积分

其中C是单位圆x2+y2=1，取逆时针方向．

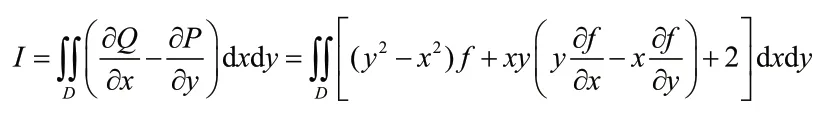
分析：上述解题过程无法得到最后的结果．从题中可知，对于曲线积分，曲线封闭且为闭区域D的正向边界．但根据题目条件仅知f(x，y)连续，故被积函数P(x，y)和Q(x，y)在区域D上是否具有一阶连续偏导数是不能确定的，因此不满足格林公式的应用条件[2]．所以直接应用格林公式是错误的，需要采用其他方法来计算这个曲线积分．

正解：对于C上任意一点(x，y)，在该点处的切向量为(-y，x)，则

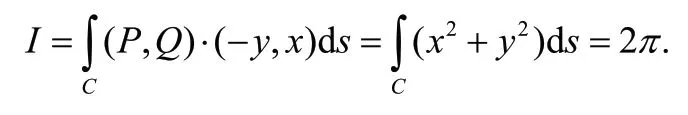
通过上面例题的分析，学生要会熟练灵活地运用格林公式求解第二类曲线积分，必须对相关的条件与结论全面地了解、掌握，在学习过程中多加练习．另一方面，在教学过程中，教师要在课堂中多与学生交流互动，更加全面地了解学生的情况．课堂上例题的选取也是教师需要考虑的问题，应尽量做到知识点的覆盖．而且，教师要及时对易错点进行探究、分析和讲评，培养学生发现问题、解决问题的 能力.