函数背景下平行四边形存在性问题的解法探讨

李小兰

[摘要]平行四边形存在性问题可用通性通法和中点公式的特殊解法求解.每一类数学问题都有通法和一些特殊方法，教学中教师应引导学生善于总结，勤于归纳，做到心中有题，题中有妙法.

[关键词]平行四边形;函数;存在性问题;中点公式

[中图分类号]G633.6

[文献标识码] A

[文章编号] 1674-6058（ 2020）35-0024-02

函数背景下平行四边形存在性问题是历年中考数学的重要考点之一，将几何图形与函数相结合进行考查更是一个热点问题，如何突破几何中的重点章节（平行四边形）和代数中的重点知识（函数）相结合的考点，是中考数学复习的重点，因此，掌握方法，找到突破口，把问题轻松解决，是教师和学生的急切需要，下面笔者以特殊的平行四边形——菱形和一般平行四边形为例讨论函数背景下平行四边形存在性问题的解法，

一、函数背景下菱形存在性问题

菱形中已知三个定点求一个动点的题目难度系数较低，一般不会在大题中出现，所以本文只论述两个定点、两个动点的情况.

菱形存在性问题大多是以“两定两动”为设问方式，其中“两定”指的是四边形四个顶点，其中有两个顶点的坐标是确定的或者是可求解的;“两动”指的是其中一个动点在一条直线或者抛物线上，另一个动点是平面内任意一点或者该动点也在一条直线或者抛物线上，

探究菱形存在性问题的具体方法如下：

（1）根据题意找出两个定点;

（2）分情况讨论：已知两个定点去探究菱形时，以两个定点确定的线段作为要探究的菱形的对角线或边长画出符合题意的菱形，结合题于要求找出满足条件的菱形;

（3）利用菱形的性质得出等量或列方程求点的坐标，要具体情况具体分析，有时也可利用直线的解析式联立方程组，根据方程组的解为交点坐标或由平移得到点的坐标，

现列举几例加以说明.

[案例1]点A和点B为平面内两个定点，点C是直线Z上一个动点，点D是平面内的一个动点，画出满足题意的菱形，

方法：要画出满足题意的所有菱形，可以转化为画等腰三角形，

如图1，以AB为菱形的边时，以B为圆心、AB为半径画圆，

如图2，以AB为菱形的边时，以A为圆心、AB为半径画圆.

如图3，以AB为菱形的对角线时，画AB的垂直平分线.

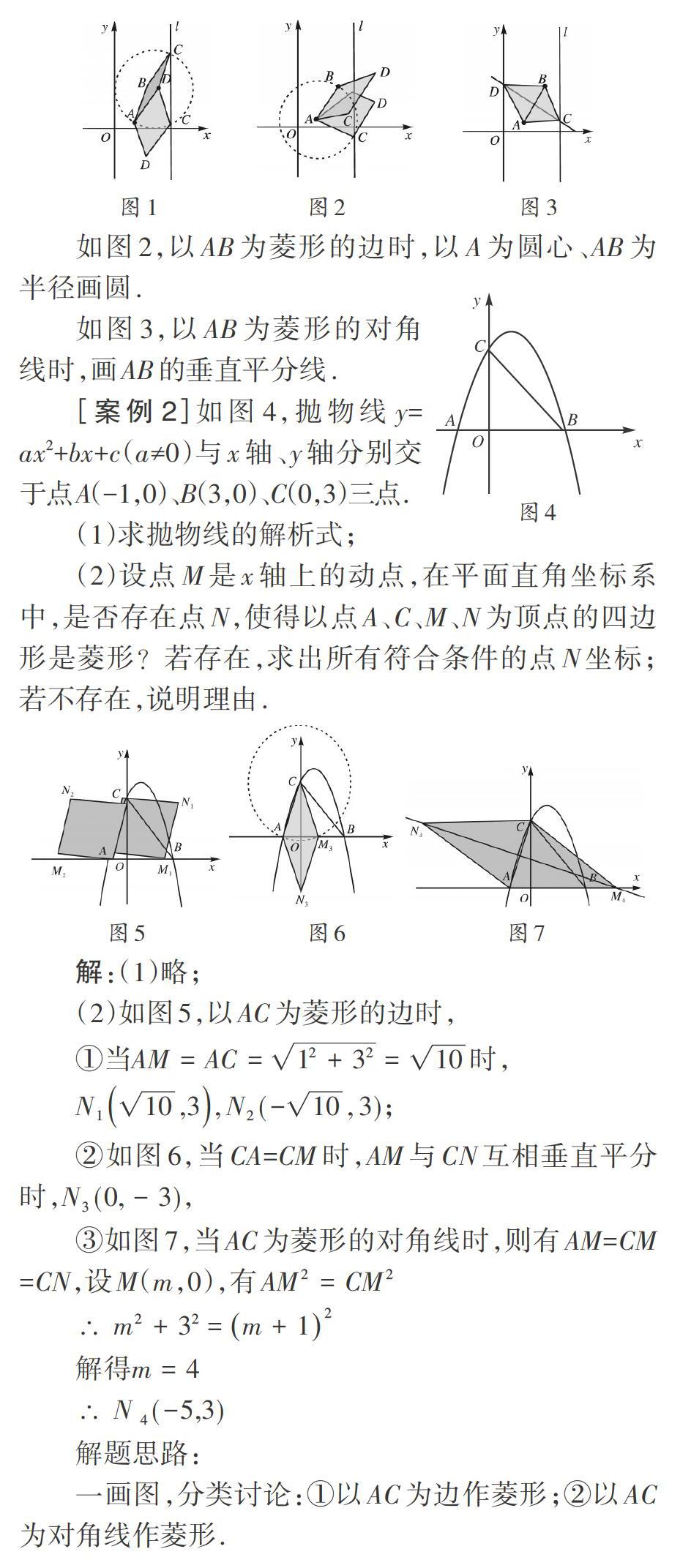
[案例2]如图4，抛物线y=ax²+bx+c（a≠0）与x轴、y轴分别交于点A（-1，0）、B（3，0）、C（0，3）三点.

（1）求抛物线的解析式;

（2）设点M是x轴上的动点，在平面直角坐标系中，是否存在点N，使得以点A、C、M、N为顶点的四边形是菱形？若存在，求出所有符合条件的点Ⅳ坐标;若不存在，说明理由，

二求点，根据图形选择适当的方法，比如勾股定理、平移、作相似三角形等，

在作图过程中，分类讨论有助于学生厘清思路，不重不漏地把图形准确地画出来，解决了作图这个难点，求点的坐标方法比较开放，学生会选择合适的方法求之，

二、平行四边形存在性问题

平行四边形中也存在两种问题，一是“三定一动”，即已知三个定点求一个动点的坐标问题，这种情况只要用三定点作出三角形，并以三角形的三边分别为对角线作出三个平行四边形即可求出动点的坐标，本文只重点讨论“两定两动”的情况，

前面讨论的菱形也属于平行四边形，所以菱形的方法在平行四边形中同样适用，这是通性通法，下面主要讨论平行四边形的特殊解法.

[案例3]如图8，抛物线经過A（-5，0），B（一1，0），C（0，5）三点，顶点为们，连接AC，BC，抛物线的对称轴为l，l与x轴交点为D，与AC交点为E，

（1）设点C'是平面内一点，是否存在以点A，B，C'，C为顶点的四边形是平行四边形？若存在，求出点C'的坐标;若不存在，请说明理由;

解题思路：如图9至图11，“三定一动”的问题，只要以BC、AC、AB分别为对角线作平行四边形，再通过平移的方法求出点C的坐标即可.

（2）设点N是抛物线上一点，点S是x轴上一点，是否存在点Ⅳ，使得以A，E，N，S为顶点的四边形是平行四边形？若存在，求出点N的坐标;若不存在，请说明理由，

解题思路：①以AE为平行四边形的边，根据“两动”限制的条件作出NS的三种情况（如图12）.结合图形过Ⅳ作NT ⊥x轴，由平行四边形性质得到△SNT≌△AED，从而得到NT= ED=2，即可得到点Ⅳ的坐标;

②以AE为平行四边形的对角线只有图13 一种情况，由平行四边形的性质可知NE//AS，可得出N与E的纵坐标相同，即可求出点Ⅳ的坐标.

这种解法类同于前面菱形的解法，都是用分类讨论的方法作图，然后根据图形选择适当的方法求出点的坐标，既然在坐标系中解题，我们可以设法用中点公式来解决，

评析：对于平行四边形的存在性问题，本题用了两种方法去解决，即通性通法和中点公式法，所用的通性通法与菱形的解题方法一样分两步走，一是画图，二是求点的坐标;利用中点公式的特殊解法是通过中点公式求点的坐标，这种方法必须先设出四个点的坐标，即四个点的坐标具有共性，便直接利用公式求点，而菱形利用中点公式求点坐标却比较麻烦，因为菱形的特殊性，每一种情况的图形中的坐标不一致，所以利用中点公式求点的坐标必须分情况计算，有时利用通性通法更简便，

当然，任何一种固定的解法都不利于培养学生的思维，但每一类数学问题都有通性通法和一些特殊方法，我们应善于总结，勤于归纳，做到心中有题，题中有妙法.

（责任编辑 陈昕）