基于局部显著边缘特征的红外图像目标轮廓跟踪算法
2020-12-11张正本
张正本,刘 丹
(1.河南工学院 计算机科学与技术学院,河南 新乡 453003;2.新乡市制造业物联网应用工程技术研究中心,河南 新乡 453003)
随着信息技术的飞速发展,单一的人工图像分析方法已经很难被人们接受,红外图像分析正成为人们关注的焦点[1]。在这一领域中,由于红外图像不能准确分析复杂背景下的图像轮廓特征,因此需要对红外图像进行有效的目标轮廓跟踪[2]。然而,在实际的跟踪过程中,大多数的目标轮廓跟踪算法无法获得红外图像目标轮廓的最佳跟踪值,导致红外图像目标轮廓跟踪陷入瓶颈[3]。针对这一问题,本文提出了一种基于复杂背景的具有局部显著边缘特征的目标轮廓跟踪算法。
1 复杂背景下红外图像目标轮廓跟踪方法
在复杂背景下的红外图像目标轮廓跟踪过程中,首先应描述红外图像的区域轮廓矢量,建立红外图像各区域的线性统计形状模型[4-6],然后得到图像各区域边界的判断阈值,给出目标轮廓模型与训练图像不动点之间的马氏距离。该方法实现了复杂背景下红外图像的目标轮廓跟踪。具体步骤如下。





为了提高复杂背景下红外图像目标轮廓的跟踪质量,首先引入射影不变量,得到红外图像中目标轮廓的射影不变量个数,然后建立目标轮廓的几何特征描述,利用Bhattacharyya系数描述目标轮廓的几何特征。具体步骤如下:

在复杂背景下的红外图像目标轮廓跟踪过程中,得到了红外图像中各区域目标轮廓的边缘检测点。计算红外图像目标轮廓的显著性[7],形成目标轮廓的特征描述向量,得到红外图像目标轮廓特征对应点坐标之间的变换关系,进而可以实现复杂背景下红外图像目标轮廓的精确跟踪。具体步骤如下:
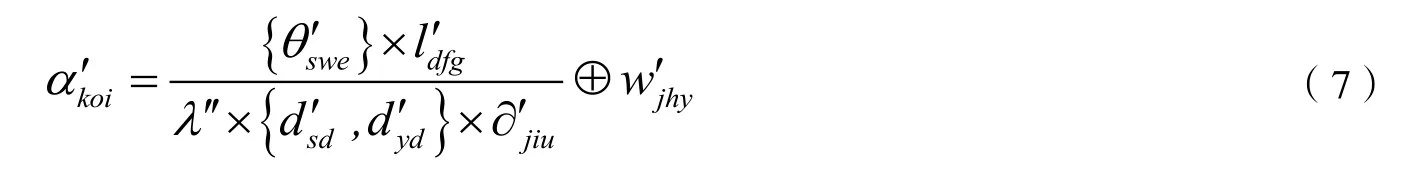


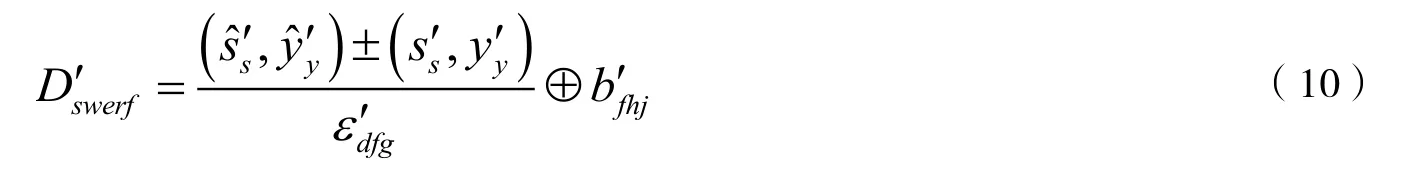

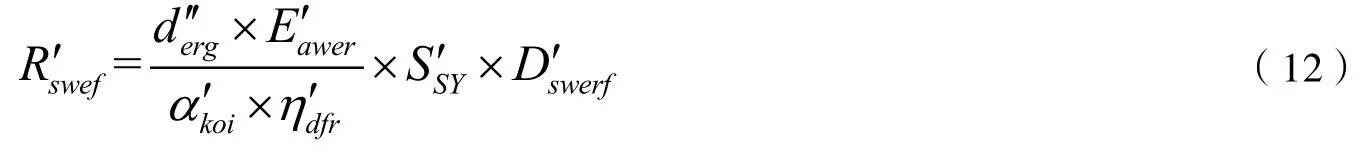
2 实验结果分析
为了验证基于局部显著边缘特征的红外图像目标轮廓跟踪算法在复杂背景下的有效性,需要进行实验。实验搭建了Matlab7.0环境下红外图像目标轮廓跟踪实验平台。所选图像是两幅不同复杂背景下的红外图像,图像大小为500×500。
2.1 评价指标设置
实验中,利用主观评价指标和客观评价指标,对复杂背景下基于局部显著边缘特征的红外图像目标轮廓跟踪算法的有效性进行了评价。以跟踪均方根误差作为主观评价指标,定义了改进跟踪算法的精度。为了突出实验的全面性和公正性,采用一种基于形态学权值的跟踪算法作为对比算法,进行常见的分析和比较。以跟踪效果作为客观评价指标,测试不同背景下红外图像目标轮廓跟踪的质量。

由公式(7)可知,RSM值越小,跟踪精度越高。
2.2 两种不同跟踪算法的均方根误差分析
采用改进的跟踪算法和基于形态学权值的跟踪算法对复杂背景下红外图像的目标轮廓进行跟踪,两种方法的均方根误差如图1所示。
从图1的实验结果可以看出,基于形态学权值的跟踪算法的均方根误差较高,约为60%,其误差曲线波动较大,误差值起伏较大,难以保证跟踪结果的准确性。采用改进的跟踪算法对复杂背景下红外图像的目标轮廓进行跟踪,均方根误差曲线稳定,平均误差在30%左右,远小于形态学加权跟踪算法的结果。这是因为改进后的算法采用了局部有效边缘目标轮廓特征向量的欧几里德距离作为目标轮廓的相似性判定度量,从而保证了红外图像目标轮廓跟踪的精度。
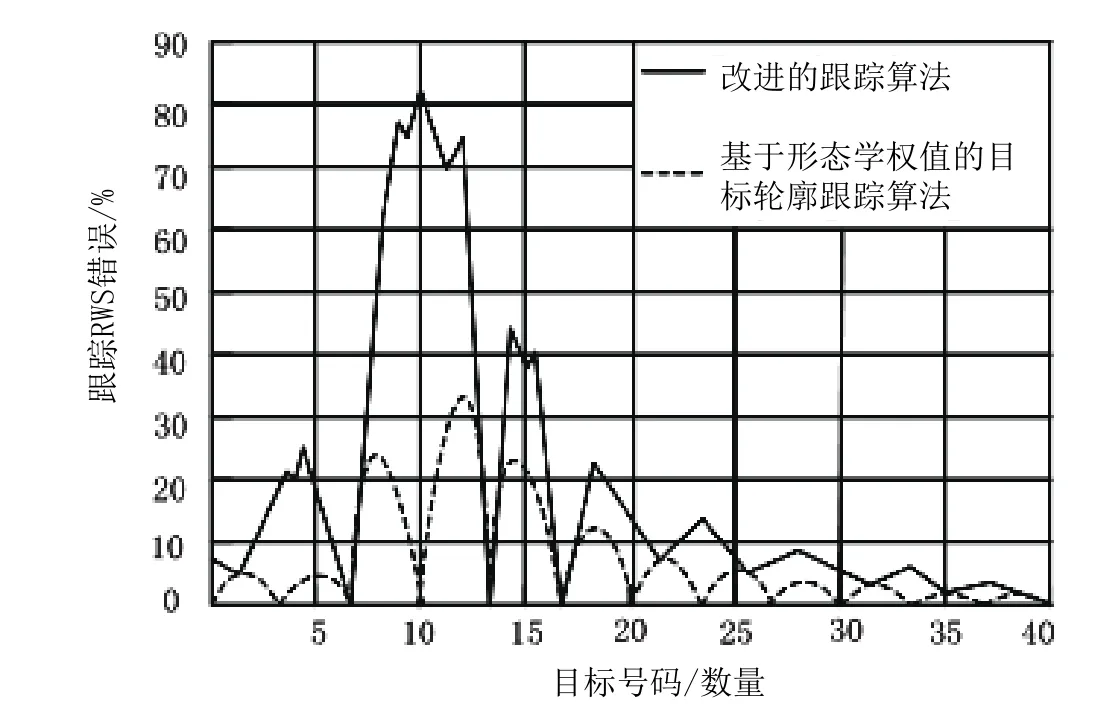
图1 两种不同算法对目标轮廓跟踪的均方根误差
2.3 不同目标轮廓跟踪方法的比较
采用改进的跟踪算法和基于形态学权值的跟踪算法对复杂背景下的红外图像目标轮廓进行跟踪,比较两种不同算法对红外图像目标轮廓的跟踪效果,如图2—4所示。
基于形态学权值的跟踪算法,无法准确跟踪目标轮廓,且跟踪结果与背景轮廓混合,跟踪结果误差较大。采用改进的算法对红外图像的目标轮廓进行跟踪,跟踪轮廓边缘与目标轮廓边缘完全匹配。与基于形态学权值的跟踪算法相比,改进后的算法能够构造出目标轮廓的几何信息描述符。利用贫化系数测量几何相似性,其结果完全满足复杂背景下红外图像目标轮廓跟踪的精度要求。

图2 原始图像

图3 基于改进算法的红外图像目标轮廓跟踪效果

图4 基于形态学权值的红外图像目标轮廓跟踪效果
3 总结
针对红外图像目标轮廓跟踪问题,提出了一种基于复杂背景局部显著边缘特征的目标跟踪算法。利用边缘方向和强度信息区域对红外图像中具有显著边缘特征的目标轮廓进行建模和搜索,形成特征描述向量,实现红外图像目标轮廓的精确跟踪。实验结果表明,该算法跟踪精度高,有效地提高了红外图像分析的质量。
