一类λ∼k数列解的情况的探究——2020年高考江苏卷第20题的探究

广东省中山市桂山中学(528463) 蔡晓波

2020年高考江苏卷第20 题给出了“λ ∼k”数列的定义,以数列为背景考察学生,该题极具创新性与探究性,笔者对该题做了探究,现将探究结果展示如下,望同行批评指正.

一、试题再现

真题(2020年高考江苏卷第20 题)已知数列ℕ+)的首项a1=1,前n项和为Sn.设λ与k是常数,若对一切正整数n,均有成立,则称此数列为“λ ∼k”数列.

(1)若等差数列{an}是“λ ∼1”数列,求λ的值;

(2)若数列{an}是数列,且an ＞0,求数列{an}的通项公式;

(3)对于给定的λ,是否存在三个不同的数列{an}为“λ ∼3”数列,且an≥0? 若存在,求λ的取值范围;若不存在,说明理由.

二、试题解法探讨与试题评析

第1,2 问的解答较为容易,留给读者完成.下面着重探讨第3 问的解法.

解法1设各项非负的数列{an}(n∈ℕ+)为“λ ∼3”数列,则

即

因为an≥0,而a1=1,所以Sn+1≥Sn ＞0,则

①若λ≤0,则由cn≥1 可得(cn −1)3≥0,λ3(c3n −1)≤0,故只有一解为cn=1,此时=1,由S1=a1=1 得Sn=1,故只有一个数列,且an=可以化为:

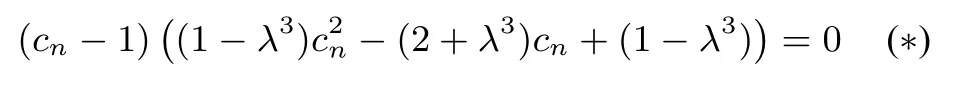
②若λ=1,则方程(∗)只有一解为cn=1,由①得只有一个数列,且an=

③若λ ＞1,则1−λ3＜0,−(2 +λ3)＜0,故故方程(∗)只有一解为cn=1.由①得只有一个数列,且an=④若0＜λ ＜1,

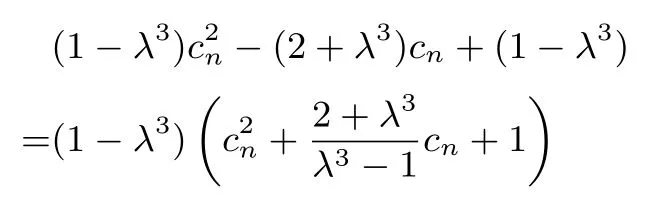
结合S1=a1=1,且an≥ 0 我们可以构造如下3 个数列:Sn=1 或Sn=或对应的通项分别为:an=或an=

综上所述,能存在三个各项非负的数列{an}为“λ ∼3”数列,λ的取值范围是0＜λ ＜1.

点评该题的3 个问设计得很好,层层递进,不断深入;第三问综合性较强,很好的考察了学生的推理、转化与综合运用数学知识探究与解决问题的能力.

第三问的难点在于学生对数列的个数与方程的解的个数之间关系的探索,从第(2)问得满足题目的数列只有一个数列,受此影响考生容易陷入一个误解,那就是方程有至少有3 个解,才会产生3 个不同的数列; 实际上根据以上解答,我们可以知道,只要方程的解有2 个或2 个以上,则必定可以构造出无数个满足题目要求的数列,为何会有如此大的差别呢? 实际上就在于第(2)问要求an ＞0,此时故(2)中的方程

只有一个解,而第(3)问an≥ 0,故即可,故只要再有另一个大于1 的解即可构造出无数个不同的且满足题目要求的数列.

解法1 实际上就是通过对λ的讨论来讨论方程根的情况,实际上根的情况等价于函数f(x)=x2+tx+1 与x轴交点个数的情况,故可以利用二次函数根的分布的相关知识来解决问题.

解法2根据解法1 可得: 若λ=1,只有一个数列满足要求,且λ /=1 时可以化为0.(cn=

要使得存在三个各项非负的数列{an}为“λ ∼3”数列,则+tcn+1=0 至少得有1 个大于1 的实数根.

设f(x)=x2+tx+1,易知Δ=t2−4=0 时,f(x)与x轴的唯一交点为(−1,0)或(1,0),故f(x)在x∈(1,+∞)至少一个交点,即2 个交点或1 个交点,分别等价于如下不等式:故或f(1)＜0,即或t ＜−2,故可得t ＜−2(第一组不等式无解,故只有1 个大于1 的交点).所以所以λ3(λ3−1)＜0,所以0＜λ ＜1,故当且仅当0＜λ ＜1时,方程+tcn+1=0 有1 个大于1 的实数根β,下面解法同解法1.

解法3根据解法1 可得:可以化为=,cn≥1,即显然,cn=1 为方程的一根,故要使得存在三个各项非负的数列{an}为“λ ∼3”数列,则方程1)=0 至少得有1 个大于1 的实数根.

由+cn+1＞0,故λ3=因为又因为cn ＞1,所以所以故0＜ λ3＜1,故当且仅当0＜ λ ＜1 时,方程=0 有1 个大于1 的实数根b,下面解法同解法1.

解法3 把方程的解转化为函数的值域问题来解决,给该类问题提供了一种较为开阔的思路.那么问题解决至此,我们不禁会思考这样一个问题: 第(3)问当k=4,5,···,甚至是n时,λ值与满足要求的数列的个数之间有什么关系呢?当又是如何呢? 把an≥0 改为an ＞0 又会有什么影响呢? 针对以上疑问,笔者做了探究,现将探究结果展示如下:

三、结论的推广与变式

在给出相关结论之前,我们先来看看一个定义和几个引理:

定义数列{an}(n∈ℕ+)的首项a1=a ＞0,前n项和为Sn,设λ与k是常数,若对一切正整数n,均有成立,则称此数列为“λ ∼k”数列.

引理1数列{an}(n∈ℕ+)的首项a1=a ＞0(a为常数),an≥0,前n项和为Sn,且对于任意的n,均有=m ＞1(m为常数),则有无数个不同的数列满足以上条件.

证明因为an≥0,所以Sn+1≥Sn ＞0,故构造数列{an}(n∈ℕ+)前n项 和 为Sn的通项为:(k∈ℕ+,k为常数.)显然当n≤k时,=1,当n=k+1 时,=m,当n≥k+2 时,=1,满足题目要求,此时对应的通项为:或n≥k+3,n∈ℕ+;因为m ＞1,故(m −1)a ＞0,故显然,对于k取不同的自然数对应的数列{an}不相同,故有无数个不同的数列满足条件.

引理2数列{an}(n∈ℕ+)的首项a1=a ＞0(a为常数),an≥0,前n项和为Sn,且对于任意的n,均有=m≥1(m为常数),则仅有一个数列满足以上条件,且通项为an=

证明因为an≥0,所以Sn+1≥Sn ＞0,故因为S1=a1=a ＞0 且=m≥1,所以{Sn}为等比数列,首项为a,公比为m,故Sn=amn−1,所以当n≥2 时,an=Sn −Sn−1=amn−1−amn−2=a(m −1)mn−2,当n=1 时,a1=S1=a,因为m≥1,a ＞0,故n=1 时a(m−1)mn−2/=a,所以an=

综上所述,仅有一个数列满足条件,且通项为an=

引理3函数f(x)=,x ＞1,k∈ℕ+为增函数,且f(x)的值域为(0,1)

证明

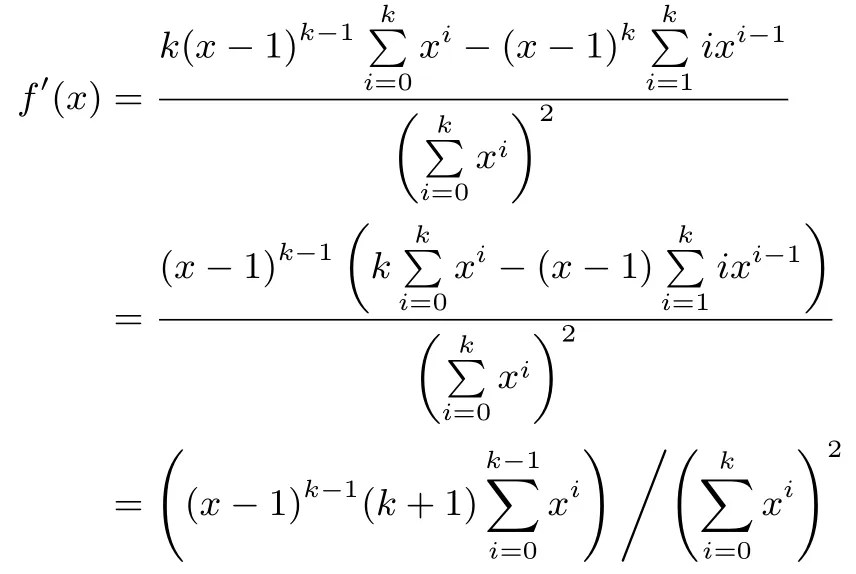
因为x ＞1 且k∈ℕ+,所以所以f′(x)＞0,所以f(x)在x∈(1,+∞)为增函数,

故当x →+∞时,f(x)→1,又因为f(1)=0.可得f(x)的值域为(0,1)

结论1数列{an}(n∈ℕ+)的首项a1=a ＞0(a为常数),an≥0,前n项和为Sn,且{an}为“λ ∼k”数列,则对于任意k≥2,k∈ℕ+,当0＜λ ＜1 时,存在无数个满足要求的不同数列{an}为“λ ∼k”数列; 当λ≤0 或λ≥1时,仅存在1 个满足要求的数列{an}为“λ ∼k”数列,且

证明因为{an}为“λ ∼k”数列,所以因为an≥0 且a1=a ＞0,所以所以可得的方程:

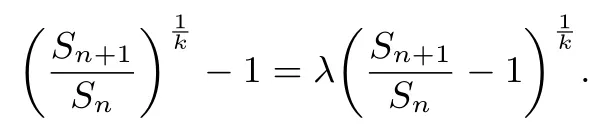
当λ≤0 时,故只有一个解当λ ＞0 时,因为k≥2,k∈ℕ+,故令cn=,cn≥1 可得:

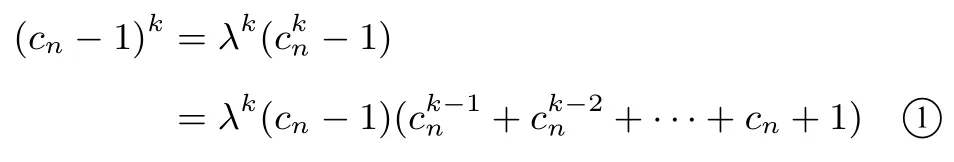
显然cn=1 为方程①的一个根,当cn /=1 时,

根据引理3 可得当0＜λk ＜1,即0＜λ ＜1 时,方程②有且只有一个大于1 的根cn=β ＞1,此时方程①有2个根cn=1 或cn=β ＞1;当λk≥1 即λ≥1 时,方程②没有大于1 的根,此时方程①只有1 个根cn=1.

结合引理1 和引理2 可得: 当0＜λ ＜1 时,存在无数个满足要求的不同的数列{an}为“λ ∼k”数列;当λ≤0 或λ≥1 时,仅存在1 个满足要求的数列{an}为“λ ∼k”数列,且

当k=3 时即为2020年高考江苏卷第20 题的第(3)问,故当0＜λ ＜1 时有无数个不同的数列{an}满足题目条件.

根据结论1,我们不难发现,若把结论条件中的an≥0修改为an ＞0,则Sn+1＞Sn,即上述证明过程中和cn=1 不再是满足要求的有效根,故上述证明过程中方程①至多只有1 个有效根,故此我们不难得出如下结论:

结论2数列{an}(n∈ℕ+)的首项a1=a ＞0(a为常数),an ＞0,前n项和为Sn,且{an}为“λ ∼k”数列,则对于任意k≥2,k∈ℕ+,当0＜λ ＜1 时,仅存在1 个满足要求的数列{an}为“λ ∼k”数列;当λ≤0 或λ≥1 时,不存在满足要求的数列{an}为“λ ∼k”数列

该结论的证明过程与结论1 类似,不再赘述.

显然,2020年高考江苏卷第20 题第(2)问满足结论2的条件,此时k=2,且λ=∈(0,1),故存在唯一满足要求的数列{an},不难求出此时方程①有一个大于1 的根cn=2,由引理2 得an=

结论3数列{an}(n∈ℕ+)的首项a1=a ＞0(a为常数),an≥0,前n项和为Sn,且{an}为“λ ∼k”数列,则对于任意k=m≥2,k∈ℕ+,当λ ＞1 时,存在无数个满足要求的不同数列{an}为“λ ∼k”数列;当λ≤1 时,仅存在1 个满足要求的数列{an}为“λ ∼k”数列,且

证明因为{an}为“λ ∼k”数列,所以m≥2,k∈ℕ+,所以由an≥0 且a1=a ＞0可得Sn+1≥Sn ＞0,所以可得的方程

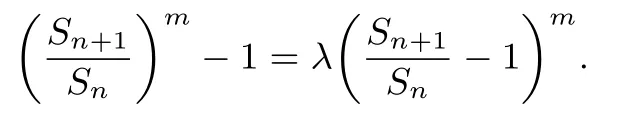
令cn=故cn≥ 1 可得方程:λ(cn −1)m.由结论1 的证明过程可知当λ≤0 上述方程只有一个实数解cn=1; 当λ ＞0 时,上述方程可化为,即

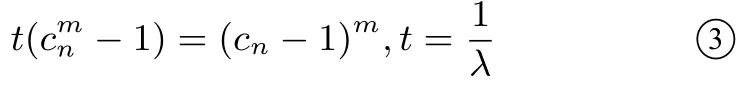
类似于结论1 的证明推理过程,我们可得: 当λ ＞1,方程③有2 个根cn=1 或cn=β ＞1;当0＜λ≤1 ③没有大于1 的根,只有1 个根cn=1.结合引理1 和引理2 可得: 当λ ＞1 时,存在无数个满足要求的不同的数列{an}为“λ ∼k”数列; 当λ≤1 时,仅存在1 个满足要求的数列{an}为“λ ∼k”数列,且

类似的我们还可得如下结论:

结论4数列{an}(n∈ℕ+)的首项a1=a ＞0(a为常数),an ＞0,前n项和为Sn,且{an}为“λ ∼k”数列,则对于任意m≥2,k∈ℕ+,当λ ＞1 时,仅存在1 个满足条件的数列{an}为“λ ∼k”数列;当λ≤1 时,不存在满足条件的数列{an}为“λ ∼k”数列

该结论的证明过程与上述结论证明类似,留给读者自己完成.另外,当k=1 时,易得如下结论:

结论5数列{an}(n∈ℕ+)的首项a1=a ＞0(a为常数),an ＞0,前n项和为Sn,且{an}为“λ ∼1”数列,则当λ=1 时,有无数个满足条件的数列{an}为“λ ∼k”数列;当λ /=1 时仅存在1 个满足条件的数列{an}为“λ ∼k”数列,且

结论6数列{an}(n∈ℕ+)的首项a1=a ＞0(a为常数),an≥0,前n项和为Sn,且{an}为“λ ∼1”数列,则当λ=1 时,有无数个满足条件的数列{an}为“λ ∼k”数列;当λ/=1 时不存在满足条件的数列{an}为“λ ∼k”数列

结论5-6 比较容易证明,留给读者自己完成.

至此,我们对“λ ∼k”数列中k为任意的正整数或正整数的倒数的情况进行了系统的讨论,并得出相关的结论.