不等式恒成立问题的解法探究*——以2020年高考全国Ⅰ卷理科数学压轴题为例

广东省深圳市高级中学(518040) 李浩宾 高 军

不等式恒成立问题作为近年来高考的热点题型,也是不等式学习中的重点与难点.本文以2020年高考全国Ⅰ卷理科数学第21 题第2 问为例,呈现问题的三种思路,五种解法,兼顾了解题的通性通法和常用解答技巧的理性思考,展示了运用多种数学思想方法进行思考的解题过程,体现了数学思想对数学解题的作用,并在解题和教学层面进行了反思,与读者交流.

一、试题呈现

题目(2020年高考全国Ⅰ卷理科第21 题)已知函数

f(x)=ex+ax2−x.

(1)当a=1 时,讨论f(x)的单调性;

(2)当x≥0 时,f(x)≥+1,求a的取值范围.

下面主要对第(2)问进行解法探究.

二、解法探究

思路一: 分离函数,数形结合

解法1(分离参数)分离参数法是通过对不等式恒等变形,使参数与主元分离于不等式两端,从而将问题转化为求主元函数的最值的解题方法.本题中的不等式含指数函数与三次函数,参数为二次项系数,比较容易分离参数.

(i)当x=0 时,f(x)≥+1 恒成立;

(ii)当x ＞0 时,f(x)≥+ 1 等价于a≥恒成立,记g(x)=则g′(x)=记h(x)=+x+1−ex,当x ＞0 时,h′′(x)=1−ex ＜0,h′(x)=x+1−ex ＜0,所以h′(x)在(0,+∞)内单调递减,h′(x)＜h′(0)=0,所以h(x)在(0,+∞)内单调递减,h(x)＜h(0)=0.所以当x∈(0,2)时,g′(x)＞0,g(x)在(0,2)内单调递增; 当x∈(2,+∞)时,g′(x)＜0,在(2,+∞)内单调递减,所以[g(x)]max=g(2)=故a≥

综上所述,a的取值范围为

评注本题分离后的函数单调性判断不复杂,原因是导函数通分后的分子能够因式分解,导函数的零点较容易求解,导函数的正负情况容易判断.因此,分离参数的原则是分离后的函数单调性容易判断,能够得到函数的最值(确界),进而解决恒成立问题.利用分离参数法来确定不等式f(x,λ)≥0(x∈D,λ为实参数)恒成立中参数λ的取值范围的基本步骤:

(1)将参数与变量分离,即化为g(λ)≥f(x)(或g(λ)≤f(x))恒成立的形式;

(2)求f(x)在x∈D上的最大(或最小)值;

(3)解不等式g(λ)≥f(x)max(或g(λ)≤f(x)min),得λ的取值范围.

解法2(分离一次函数)当x=0 时,f(x)≥+1恒成立; 当x ＞0 时,f(x)≥+ 1 等价 于ax≥恒成立,记g(x)=则记h(x)=x2+x+1−ex,当x ＞0 时,h′(x)=2−ex,h′′(x)=2x+1−ex,所以h′(x)在(0,ln 2)内单调递增,在(ln 2,+∞)内单调递减,而且h′(0)=0,h′(1)=3−e＞0,h′(2)=5−e2＜0,所以存在x0∈(1,2),h′(x0)=0,此时当x∈(0,x0)时,h(x)＞0,当x∈(x0,+∞)时,h(x)＜0,所 以g(x)在(0,1)内 单调递减,在(1,x0)内单调递增,在(x0,+∞)内单调递减,且g(0)=0,则g(x)=的图象如图所示,原不等式恒成立等价于y=ax的图象位于y=g(x)的图象上方,临界情况是两函数图象相切.当y=ax与y=g(x)的图象相切时,设切点坐标为(m,t),则a=g′(m)=am=g(m)=解得m=2,a=故a的取值范围是

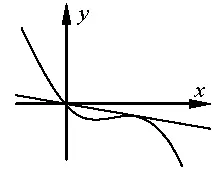
评注所给不等式进行合理的变形化为f(x)≥g(x)(或f(x)≤g(x)),能较容易地作出不等号两边函数的图象,由数形结合直接判断得出结果.

思路二: 构造含参函数,进行分类讨论

解法3因为f(x)≥+1 等价于x −1≥0,构造函数g(x)=ex −+ax2−x −1(x≥0),则g′(x)=ex −+ 2ax −1,g′′(x)=ex −3x+ 2a,g′′′(x)=ex −3,且g(0)=0,g′(0)=0,g′′(0)=1+2a.所以g′′(x)在(0,ln 3)内单调递减,在(ln 3,+∞)内单调递增,此时[g′′(x)]min=g′′(ln 3)=2a+3(1−ln 3).

(i)若2a+3(1−ln 3)≥0,即a≥则g′(x)在(0,+∞)内单调递增,g′(x)≥0,g(x)在[0,+∞)内单调递增,g(x)≥g(0)=0,不等式恒成立;

(ii)若2a+ 1≤0,即a≤则当x∈(0,ln 3),g′′(x)＜0.所以g′(x)在(0,ln 3)内单调递减,而g′(0)=0,故当x∈(0,ln 3)时,g(x)在(0,ln 3)内单调递减,不合题意.

若g′(x2)≥0,则g′(x)≥0 恒成立,g(x)在[0,+∞)内单调递增,g(x)≥g(0)=0,不等式恒成立; 若g′(x2)＜0,则存在x3∈(x1,x2),x4∈(x2,+∞),g′(x3)=g′(x4)=0,此时g(x)在(0,x3)内单调递增,在(x3,x4)内单调递减,在(x4,+∞)内单调递增,且g(0)=0,要使g(x)≥ 0恒成立,只需要g(x4)=0,此时g′(x4)=ex4−2ax4−1=0,g(x4)=−x4−1=0,消去a,得(x4−2)=0,解得x4=2,由g(x4)≥0得a≥,故综上,a的取值范围是

解法4f(x)≥+1 等价于1,构造函数g(x)=(x≥0),则

(i)若2a+1≤0,即a≤则当x∈(0,2),g′(x)＞0.所以g(x)在(0,2)内单调递增,而g(0)=1,故当x∈(0,2)时,g(x)＞1,不合题意.

(ii)若0＜2a+ 1＜2,即则当x∈(0,2a+1)∪(2,+∞)时,g′(x)＜0,当x∈(2a+1,2)时,g′(x)＞0.所以g(x)在(0,2a+1),(2,+∞)内单调递减,在(2a+1,2)内单调递增.由于g(0)=1,所以g(x)≤1当且仅当g(2)=(7−4a)e−2≤1,即a≥,所以当时,g(x)≤1.(iii)若2a+1≥2,即则g(x)≤由于0∈故由(ii)可得1,故当时,g(x)≤1.

综上,a的取值范围是

评注比较这两种解法,解法3 直接移项构造函数,想法简单,但后续涉及到一、二阶导数的讨论,比较复杂,而且涉及x4=2 的求解,难以完成.解法4 构造巧妙,注意到的导函数因式分解,能求解零点,讨论相对比较简单.构造含参函数解决不等式恒成立的一般思路:

f(x)＞0 恒成立⇔f(x)min＞0 (注: 若f(x)的最小值不存在,则f(x)＞0 恒成立⇔f(x)的下界大于0);f(x)＜0 恒成立⇔f(x)max＜0(注: 若f(x)的最大值不存在,则f(x)＜0 恒成立⇔f(x)的上界小于0).

思路三: 必要性探路,再证充分性

解法5当x=2 时,a≥下证当a=时,原不等式成立.此时f(x)≥+ 1 等价于设函数g(x)=ex −+−x−1(x≥0),则g′(x)=ex −x−1,g′′(x)=ex −3x+,g′′′(x)=ex −3,且g(0)=0,g′(0)=0,g′′(0)=＞0.所以g′′(x)在(0,ln 3)内单调递减,在(ln 3,+∞)内单调递增.

由[g′′(x)]min=g′′(ln 3)=−3 ln 3＜0,g′′(2)=＞0 可知存在x1∈(0,ln 3),x2∈(ln 3,2),g′′(x1)=g′′(x2)=0,此时g′(x)在(0,x1)单调递增,在(x1,x2)单调递减,在(x2,+∞)单调递增,且g′(0)=g′(2)=0.所以存在x3∈(x1,x2),g′(x3)=0,此时当x∈(0,x3)时,g′(x)＞0,当x∈(x3,2)时,g′(x)＜0,当x∈(2,+∞)时,g′(x)＞0.所以g(x)在(0,x3)单调递增,在(x3,2)单调递减,在(2,+∞)单调递增,且g(0)=g(2)=0,故g(x)≥0.当a=时,原不等式成立.

综上,a的取值范围是

评注在给定区间上适当考虑某点(端点)的性质,取x的特殊值,得到参数的取值范围,找到一个不等式成立的必要条件,从而缩小范围,然后再证明必要条件也是充分条件,即可求得结论,就是我们常说的必要性探路法.而端点效应是其中比较常见的一种题型,比如2019年新课标全国Ⅰ卷文科第20 题体现了这样的解题思路.

结语不等式恒成立求参数范围问题,往往涉及函数、方程、不等式等高中数学核心知识,以及函数与方程、转化与化归、分类讨论、数形结合等数学思想,综合性强、难度大.解决此类问题的通法是构造函数,对参数进行分类讨论求解;也可以优先采用分离函数方法,将问题转化为求函数的最值,或借助数形结合思想求解;然而并非所有问题用这两种思路容易奏效,这时我们可以采用必要性探路,再证充分性的思路.学生在实际解题中,需结合具体问题进行具体分析,选择合适的解题思路与方法,让问题的解决简洁、高效.