2020年高考全国卷导数压轴题解法分析及备考建议

2020-12-11湖南省怀化市铁路第一中学418000

中学数学研究(广东) 2020年21期

关键词：实根零点评析

湖南省怀化市铁路第一中学(418000) 高用

1 试题的求解与评析

题目1(2020 高考全国1 卷理科第21 题)已知函数f(x)=ex+ax2−x.

(1)当a=1 时,讨论f(x)的单调性;

(2)当x≥0 时,f(x)≥求a的取值范围.

解析(1)当a=1 时,f(x)=ex+x2−x,则f′(x)=ex+2x −1,因为f′(x)在ℝ 上单调递增,而f′(0)=0,所以当x∈(−∞,0)时,f′(x)＜0,当x∈(0,+∞)时,f′(x)＞0,故f(x)在(−∞,0)上单调递减,在(0,+∞)上单调递增.

(2)解法1当x≥0 时,f(x)≥+1,即ex+ax2−x≥+1,显然,当x ＞0 时,上不等式成立.当x ＞0 时,不等式等价于,令g(x)=x ＞0,则

令h(x)=x3−2x −4−2(x −2)ex,x ＞0,则h′(x)=3x2−2−2(x −1)ex,所以h′′(x)=6x −2xex=2x(3−ex),由h′′(x)＞0,解得0＜x ＜ln 3,所以h′(x)在(0,ln 3)上单调递增,在(ln 3,+∞)上单调递减,

故当x∈(0,ln 3)时,h′(x)＞h′(0)=0,而h′(2)=2(5−e2)＜0,所以h′(x)在(ln 3,+∞)内存在唯一零点x0,且x0∈(ln 3,2),使得当x∈(ln 3,x0)时,h′(x)＞0,当x∈(x0,+∞)时,h′(x)＜0,所以h(x)在(0,x0)上单调递增,在(x0,+∞)上单调递减.从而当x∈(0,x0)时,h(x)＞h(0)=0,而h(2)=0,则x=2 是h(x)的唯一零点,且当x∈(0,2)时,h(x)＞0,则g′(x)＞0,所以g(x)单调递增; 当x∈(2,+∞)时,h(x)＜0,则g′(x)＜0,所以g(x)单调递减,所以g(x)max=g(2)=由题意,

综上,a的取值范围为

解法2当x≥ 0 时,f(x)≥+ 1,即ex+等价于1+≥0,令g(x)=+ 1,x≥ 0,则g′(x)=若2a+ 1≤0,即时,g′(x)＞0 的解集为(2,+∞),则g(x)在[0,2)上单调递减,在(2,+∞)上单调递增,所以g(x)min=g(2)=由题意得≥0,解得a≥矛盾.

若0＜2a+1＜2,即时,g′(x)＞0 的解集为(0,2a+1)∪(2,+∞),所以g(x)在[0,2a+1)上单调递增,在(2a+1,2)上单调递减,在(2,+∞)上单调递增.故当x∈[0,2a+1)时,g(x)≥g(0)=0,要使得g(x)≥0在[0,+∞)上恒成立,则g(2)≥0,即≥0,解得若2a+1=2,即时,g′(x)≥0,则g(x)在[0,+∞)上单调递增,所以g(x)≥g(0)=0,满足题意.

若2a+ 1＞2,即a ＞时,g′(x)＞0 的解集为(0,2)∪(2a+ 1,+∞),所以g(x)在[0,2)上单调递增,在(2,2a+1)上单调递减,在(2a+1,+∞)上单调递增.故当x∈[0,2)时,g(x)≥g(0)=0,要使得g(x)≥0 在[0,+∞)上恒成立,则g(2a+1)≥0,即

令t=2a+ 1,则+ 1≥ 0,令h(t)=+1,则h′(t)=＞0,所以h(t)在(2,+∞)上单调递增,故h(t)＞h(2)=1−＞0,满足题意,所以

综上,a的取值范围为

评析本题是一道不等式恒成立问题,此题的难点在于不等式由指数和3 次函数的简单组合,次数比较高,多次求导可以降幂,但有参数不容易求根,所以直接作差构造函数的最值法行不通.为了解决以上的这个困难,可以从两个方面着手: 一是分离参数,将参数从函数中分离出来,然后通过多次求导降幂,从而求出导数的根,得到函数单调性,最终求出函数的最值,使得问题得解; 二是“消去”指数ex,通过不等式两边同时除以ex,从而构造一个以ex为分母的分式函数,求导之后转化为x(x −2)[x −(2a+1)],然后便可以讨论单调性求最值,进而求出参数a的取值范围.正是由以上的两种处理思路得到了解法1 和解法2.

本题虽然是常规题型,却是常规中有新意,很好得考查学生遇到问题、分析问题、解决问题的能力,对灵活运用导数工具求解问题要求较高.

题目2(2020年高考全国Ⅱ卷理科第21 题)已知函数f(x)=sin2xsin 2x.

(1)讨论f(x)在区间(0,π)的单调性;

(2)证明:|f(x)|≤

(3)设n∈ℕ∗,证明: sin2xsin22xsin24x···sin22nx≤

解析(1)

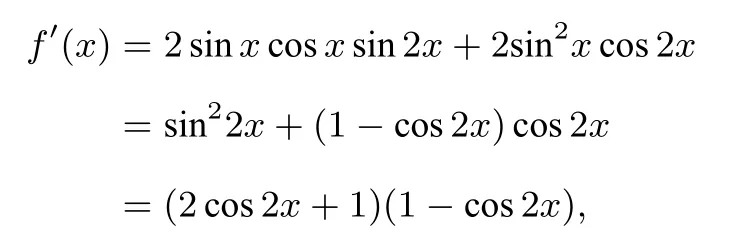
因为x∈(0,π),由f′(x)＞0,解得0＜ x ＜或所以f(x)在上单调递增,在上单调递减,在上单调递增.

(2)证明: 因为f(x+π)=sin2(x+π)sin 2(x+π)=sin2xsin 2x=f(x),所以f(x)是以π为周期的周期函数.由(1)知,当x∈(0,π)时,f(x)在上单调递增,在上单调递减,在上单调递增,又所以故有|f(x)|≤所以,x∈ℝ,|f(x)|≤

(3)证明: 由(2)知,|f(x)|≤则即sin4xsin22x≤所以sin4xsin62xsin64x···sin62n−1xsin22nx≤,又sin2x≤1,sin42nx≤1,所以

试题出处华东师范大学出版社《奥数教程》高一分册第14 讲《三角不等式》练习题B 组15 题:

评析本题应该是上述的一道竞赛题改编而成,将证明不等式所需构造的函数以题干的形式给出,通过设置三问,逐步引导,层层递进,大大降低了难度,使之成为了一道合适的高考试题.

本题是一道三角不等式问题,含三角的函数最大的难点在于函数单调性往往比较复杂,此类问题一般需要借助其周期性、对称性、有界性等来进行求解.对本题来说,利用其周期为π,研究在(0,π)内的单调性、值域,从而得到整个定义域内的值域,再借助第二问的不等式,结合第三问要证不等式的结构特点,不难得到证明思路.

题目3(2020年高考全国Ⅲ卷理科第21 题)设函数f(x)=x3+bx+c,曲线y=f(x)在点处的切线与y轴垂直.

(1)求b;

(2)若f(x)有一个绝对值不大于1 的零点,证明:f(x)所有零点的绝对值都不大于1.

BOTDR是布里渊散射光时域反射测量技术(Brillouin Optical Time Domain Reflectometry)的缩写，是一种分布式应变监测技术，属于滑坡地表位移测线型监测技术。其基本原理是利用光纤中的自然布里渊散射光的频移变化量与光纤所受的轴向应变和温度的线性关系，得到光纤的轴向应变，进而求出轴向位移[21]，根据BOTDR接收到的布里渊散射光频率，即可完成光纤上各点的定位和测量。布里渊散射光频率的漂移量与光纤的轴向应变和温度的关系与可用下式表示：

解析(1)f′(x)=3x2+b,由题意得即

(2)解法1f(x)=x3−+c,则f′(x)=3x2−=由f′(x)＞0,解得所以f(x)在(−∞,)上单调递增,在上单调递减,在上单调递增,所以f(x)在x=处取极大值处取极小值

若c+＜0,即c ＜时,f(x)只有一个零点,因为f(1)=c+＜0,所以该零点大于1,不满足题设.若c −＞0,即c ＞时,f(x)只有一个零点,因为f(−1)=c −＞0,所以该零点小于−1,不满足题设.若即c=时,f(x)有两个零点x=和x=1,此时f(x)所有零点的绝对值都不大于1.若c −=0,即时,f(x)有两个零点和x=−1,此时f(x)所有零点的绝对值都不大于1.若c+＞0 且c −＜0,即所以f(x)在内存在唯一零点x0,又f(−1)=c −14＜0,所以f(x)在(−∞,)内存在唯一零点x1∈(−1,−),而f(1)=c+＞0,所以f(x)在内存在唯一零点

综上,若f(x)有一个绝对值不大于1 的零点,f(x)所有零点的绝对值都不大于1.

评析本题是一道函数零点问题,所研究的函数就是一个三次函数,可以说非常简单,只需结合函数单调性及函数极值进行分类讨论,然后利用零点存在定理进行“卡根”即可得到零点的范围.

下面给出一种利用三次实系数方程根与系数的关系处理的解法:

解法2f(x)=0,即x3−+c=0.若方程+c=0 只有1 个实根,如果该实根的绝对值不大于1,则f(x)所有零点的绝对值都不大于1;如果该实根的绝对值大于1,则不满足题设.若方程+c=0 有3 个实根(包括其中有两个相等实根的情况),设这3 个实根分别为x1,x2,x3,由韦达定理,有x1+x2+x3=0,x1x2+x2x3+x3x1=则=(x1+x2+x3)2−2(x1x2+x2x3+x3x1)=

所以至多有一个实根的绝对值大于1,不妨设|x1| ＞1,则|x2+x3|=|−x1|=|x1| ＞1,从而1＜(x2+x3)2=故矛盾.所以方程+c=0的3 个实根的绝对值都不大于1.

综上,若f(x)有一个绝对值不大于1 的零点,f(x)所有零点的绝对值都不大于1.

题目4(2020年高考全国新课标Ⅰ卷第21 题)已知函数f(x)=aex−1−lnx+lna.

(1)当a=e 时,求曲线y=f(x)在点(1,f(1))处的切线与两坐标轴围成的三角形的面积;

(2)若f(x)≥1,求a的取值范围.

解析当a=e 时,f(x)=ex−lnx+1,则f′(x)=所以f′(1)=e−1,f(1)=e+1,故曲线y=f(x)在点(1,f(1))处的切线方程为y −(e + 1)=(e−1)(x −1),即y=(e−1)x+ 2.令x=0,得y=2; 令y=0,得所以切线与两坐标轴围成的三角形的面积为

(2)解法1f′(x)=令0,因为a ＞0,易得g(x)在(0,+∞)上单调递增,又x →0时,g(x)→−∞;x →+∞时,g(x)→+∞,所以存在唯一x0∈(0,+∞)使得g(x0)=0,即aex0−1−=0,则a=那么,当x∈(0,x0)时,g(x)＜0,即f′(x)＜0,则f(x)单调递减,当x∈(x0,+∞)时,g(x)＞0,即f′(x)＞0,则f(x)单调递增,所以

由题意,f(x)min≥1,即−2 lnx0−x0+ 1≥1,即−2 lnx0−x0≥0.令h(x)=−2 lnx −x,易知h(x)在(0,+∞)上单调递减,又h(1)=0,所以不等式−2 lnx0−x0≥0 的解集为(0,1].而则,x0∈(0,1],令φ(x)=xex−1,x∈(0,1],则φ′(x)=(x+1)ex−1＞0,所以φ(x)在(0,1]上单调递增,故φ(x)∈(0,1],则∈(0,1],所以a∈[1,+∞).所以,a的取值范围为[1,+∞).

解法2f(x)≥ 1,即aex−1−lnx+ lna≥ 1,则elna+x−1−lnx+lna≥1,得elna+x−1+lna+x−1≥lnx+x,令g(x)=ex+x,则g(lna+x −1)≥g(lnx).易知g(x)在(0,+∞)上单调递增,所以原不等式等价于lna+x−1≥lnx,则lna≥lnx −x+1.

令h(x)=lnx −x+1,则所以当x∈(0,1)时,h′(x)＞0,h(x)单调递增,当x∈(1,+∞)时,h′(x)＜0,h(x)单调递减,故h(x)max=h(1)=0.由题意,lna≥h(x)max=0,得a≥1.所以,a的取值范围为[1,+∞).

评析本题也是一道不等式恒成立问题,处理的难点在于含参数“双超越”结构,直接构造函数求导之后无法求出根需要假设“隐零点”,所以该题也是一道“隐零点”问题.“隐零点”问题处理的关键是“隐零点”与参数之间的代换,本题是将函数f(x)的最小值代换为关于“隐零点”x0的式子,通过解关于x0的不等式得到x0的取值范围,再利用参数a与x0的关系解出a的取值范围.

另外,“双超越”结构的函数往往都具备一定的对称性,可以利用这种对称性进行代数变形构造同构式,再借助函数单调性,从而将原不等式等价转化为较为简洁的“单超越”不等式.

2 复习备考的建议

2.1 重视基础,回归本质

可以看出,2020年全国卷的几道导数压轴试题难度都不大,而且题型也很常规,涉及到不等式恒成立、不等式证明和函数零点,注重对函数与导数最基础知识和方法的考查,利用函数单调性、函数极值、最值、零点存在定理等处理、解决不等式恒成立、不等式证明和函数零点问题.所以,对导数大题的复习备考要淡化技巧,重视基础,回归本质,突显导数研究函数问题的工具性作用,重点掌握导数研究函数问题的基本思想和方法,要注重通解通法,注重题型及其求解方法的归纳.