一道椭圆试题的多角度探究

内蒙古巴彦淖尔市第一中学(015000) 杨松松 王东伟

1 试题呈现

题目(长春市普通高中2020 届高三质量监测(二))已知椭圆C:=1(a ＞b ＞0)的左、右顶点分别为A、B,焦距为2,点P为椭圆上异于A、B的点,且直线PA和PB的斜率之积为

(1)求C的方程;

(2)设直线AP与y轴的交点为Q,过坐标原点O作OM//AP交椭圆于点M,试探究是否为定值,若是,求出此定值;若不是,请说明理由.

2 解法探究

解(1)设点P(xP,yP),则=1,又A(−a,0),B(a,0),kPA ·kPB=因此又2c=2,所以

第(2)问可用以下三种方法解答.

解法一设点P(xP,yP),Q(xQ,yQ),则xQ=0.由题意可知,直线AP的斜率存在且不为零,设直线AP的斜率为k,则AP:y=k(x+2),OM:y=kx.联立直线AP与椭圆C的方程并整理得,(3+4k2)x2+16k2x+4=0,注意到−2,xP是上式的两根,所以−2+xP=因此联立直线OM与椭圆C的方程并整理得,(3+4k2)x2=12,注意到xM是上式的根,则所以=2(为定值).

解法二设点P(xP,yP),Q(xQ,yQ),设直线AP的方程为

直线OM的方程为x=my.联立直线AP与椭圆C的方程并整理得,(3m2+4)y2−12my=0,解得y=0 或y=因此yP=由①式可知,当x=0时,y=,因此yQ=.联立直线OM与椭圆C的方程并整理得,(3m2+4)y2=12,解得y2=因此=2(为定值).

解法三设直线AP的倾斜角为α,则直线AP的参数方程为(t是参数),直线OM的参数方程是(t是参数),把直线AP的参数方程代入到椭圆C的方程并整理得,(3cos2α+4sin2α)t2−12 cosαt=0,解得t=0 或t=则

把直线OM的参数方程代入到椭圆C的方程并整理得,(3cos2α+4sin2α)t2=12,解得t2=所以

点评三种解法的区别在于直线AP方程的形式不同,这使得试题的解法具有多样性,为考生提供了广阔的空间,而三种方法的本质都是解析法,这是解决解析几何问题的核心方法.

3 题目的一般化

将题目一般化可以得出:

性质1已知椭圆C:=1(a ＞b ＞0)的左顶点为A,P为椭圆C上异于点A的一点,直线AP与y轴交于点Q,过坐标原点O作OM//AP交椭圆C于点M,则

4 问题的推广

将坐标原点推广到不在椭圆上的任意一点可以得出:

性质2已知椭圆C:=1(a ＞b ＞0)的左顶点为A,P为椭圆C上异于A的一点,直线AP与y轴交于点Q,过点R(x0,y0)(不在椭圆C上)的直线与椭圆C交于M,N两点,若直线AP//MN,则为定值

证明设直线AP的倾斜角为α,则直线AP的参数方程为(t是参数),直线MN的参数方程为(t是参数),把直线AP的参数方程代入到椭圆C的方程并整理得,(b2cos2α+a2sin2α)t2−2b2acosαt=0,解得t=0 或t=所以把直线MN的参数方程代入到椭圆C的方程并整理得,

(b2cos2α+a2sin2α)t2+(2b2x0cosα+2a2y0sinα)t+b2x20+a2y20−a2b2=0,设点M,N对应的参数分别为t1,t2,则t1,t2是上式的两根,所以因此|RM|·|RN|=|t1|·所以

将y轴推广到直线x=m(m/=±a)可以得出:

性质3已知椭圆C:=1(a ＞b ＞0)的左顶点为A,P为椭圆C上异于A的一点,直线AP与直线x=m(m /=±a)交于点Q,过点R(x0,y0)(不在椭圆C上)的直线与椭圆C交于M,N两点,若直线AP//MN,则为定值

证明设直线AP的倾斜角为α,则直线AP的参数方程为(t是参数),直线MN的参数方程为(t是参数),直线AP的参数方程中,令x=m得,t=所以|AQ|=由性质2 的证明过程可知,|AP|=所以

再将椭圆的左顶点推广到椭圆上任意一点可以得出:

性质4已知A(m,n)是椭圆C:=1(a ＞b ＞0)上任意一点,过点A的直线交椭圆C于另一点P,交直线b2mx+a2ny+s=0(s/=−a2b2)于点Q,过点R(x0,y0)(不在椭圆C上)的直线与椭圆C交于M,N两点,若直线AP//MN,则为定值

证明设直线AP的倾斜角为α,则直线AP的参数方程为(t是参数),直线MN的参数方程为(t是参数),把直线AP的参数方程代入到椭圆C的方程并整理得,

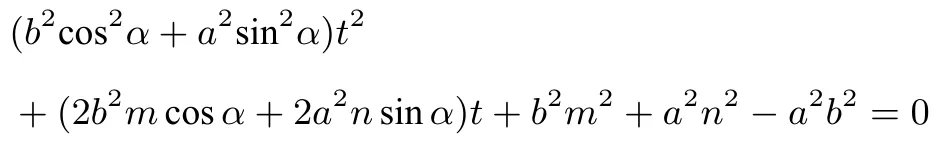
因为点A(m,n)在椭圆C上,所以

于是,(b2cos2α+a2sin2α)t2+(2b2mcosα+2a2nsinα)t=0,解得t=0 或所以

把直线AP的参数方程代入到直线方程b2mx+a2ny+s=0并整理得(b2mcosα+a2nsinα)t+b2m2+a2n2+s=0,注意到④式,因此(b2mcosα+a2nsinα)t+a2b2+s=0,由已知条件可知a2b2+s/=0,所以t=所以

由性质2的证明过程可知,|RM|·|RN|=再由⑤⑥可得

5 类比到双曲线和抛物线中

性质5已知A(m,n)是双曲线C:=1(a ＞0,b ＞0)上任意一点,过点A的直线交双曲线C于另一点P,交直线b2mx −a2ny+s=0(s /=−a2b2)于点Q,过点R(x0,y0)(不在双曲线C上)的直线与双曲线C交于M,N两点,若直线AP//MN,则|AP|·|AQ||RM|·|RN|为定值

性质6已知A(m,n)是抛物线C:y2=2px(p ＞0)上任意一点,过点A的直线交抛物线C于另一点P,交直线px −ny+s=0(s /=pm)于点Q,过点R(x0,y0)(不在抛物线C上)的直线与抛物线C交于M,N两点,若直线AP//MN,则为定值

性质5、6 的证明过程可类比性质4 完成.