巧用蒙日圆 妙解一类题
2020-12-11江西省瑞金第一中学342500魏东升
江西省瑞金第一中学(342500) 魏东升
我们可能都曾有过这种感受,就是明明对一种事物很熟悉,但随着我们对其了解的深入,却出现了越来越陌生的感觉,比如从小到大伴随我们成长的圆,可谓是大家最熟悉的图形之一了.但是当其以阿波罗尼斯圆、蒙日圆等这类隐形圆的身份出现在高考题中时,不少人却陌生了.为此,本文通过例举蒙日圆在部分有心二次曲线(有对称中心的二次曲线)问题上的应用,来让大家感受运用蒙日圆解题的美妙.
在有心二次曲线中,任意两条相互垂直的切线的交点都在同一个圆上,它的圆心是有心二次曲线的中心,半径由有心二次曲线的二次项系数决定,这个圆就是蒙日圆.用符号语言可以表示为:
定理若过一动点P能向有心二次曲线C:mx2+引两条相互垂直的切线,则该动点P的轨迹是一个圆,其方程为:(当C为双曲线时,此轨迹不含与渐近线的交点).
证明假设点P(x0,y0),当两条切线斜率存在且不为0时,设其斜率分别为k1和k2,并设经过点P的切线方程为:y=k(x −x0)+y0,与曲线C的方程mx2+ny2=1 联立消去y整理得:
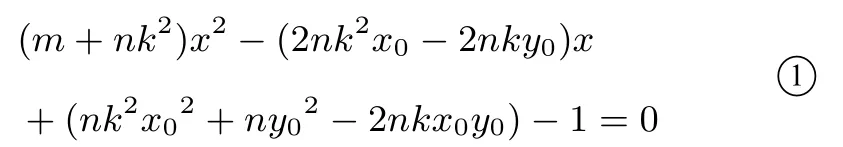

当m+nk2/=0 时,整理得: (n−mnx02)k2+2mnkx0y0−mny02+m=0,可知k1和k2是该方程的两个根,所以k1k2==−1,整理得:

当m+nk2=0 时,方程①为关于x的一次方程,即不存在满足题意的两条相互垂直的切线,此时的点P刚好在双曲线的渐近线上; 当C为双曲线时,满足题设的两条直线斜率存在且不为0;当C不为双曲线时,满足题设的两条直线斜率不存在或为0,此时点P的坐标为或满足方程②.
综上所述,点P的轨迹方程为:x2+y2=(当C为双曲线时,此轨迹不含与渐近线的交点).
以下笔者将分别从圆、双曲线和椭圆等三个角度例析蒙日圆的应用.
1 蒙日圆与圆
例1过椭圆=1(a >b >0)上点P作圆C2:x2+y2=b2的两条相互垂直的切线,则椭圆C1的离心率的取值范围是____.
通解设椭圆C1的左顶点为A,圆C2上的两个切点为M,N.因为椭圆C1的左右顶点离圆C2最远,所以椭圆上的点和切点所形成的∠MPN中,∠MAN最小,从而要使椭圆C1上的点P作得的圆C2的两条切线相互垂直,则必须满足最小的∠MAN≤如图1,此时即2b2≤a2,解得

图1
妙解由定理可知,点P是在圆C2的蒙日圆上,其轨迹方程为:x2+y2=b2+b2=2b2.又点P在椭圆C1上,所以椭圆C1和圆C2有公共点,所以2b2≤a2,解得
评析本题通解运算量看似不逊色于妙解,但其难点在于能够及时把“椭圆C1上的点P作圆C2的两条切线能相互垂直”转化为“∠MAN≤并且还需要知道“∠MAN≤和离心率的联系,对学生的思维能力和素养要求较高.从这点来说,蒙日圆的优势不言而喻.
2 蒙日圆与双曲线
例2已知双曲线=1(a >0,b >0)的离心率为过点E(−1,0)的双曲线的两条切线相互垂直,则双曲线C的标准方程为____.
通解易知过点E的直线切双曲线于左支.不妨设在x轴上方的切点为M,x轴下方的切点为N,由双曲线的对称性可得直线ME的方程为y=−x −1,由所以双曲线的标准方程为=1,和方程y=−x −1 联立得:3x2+ 12x+ 6 + 2c2=0,由Δ=0 解得c=从而所以双曲线C的标准方程为−y2=1.
妙解由定理可知,点E其实是在双曲线C的蒙日圆上,其轨迹方程为:x2+y2=所以又双曲线离心率解得所以双曲线C的标准方程为
评析“直线和双曲线相切”这个条件的处理并不像“直线和圆相切”那么方便明了,常规的办法只能是通过联立方程后令判别式为0,即便是能想到“切线斜率与原点到切点连线斜率的乘积为定值”这一定值结论,较之妙解也免不了相当的运算量.
3 蒙日圆与椭圆
例3如图2,若矩形ABCD的四条边都与椭圆相切,则矩形ABCD面积的最大值为____.

图2
通解假设点A(x0,y0),当AB,AD斜率存在且不为0 时,设其斜率分别为k1和k2,设过点A的直线方程y=k(x −x0)+y0.代入椭圆方程整理得:

整理得: (x02−4)k2−2x0y0k+y02−3=0((x02/=4),可知k1和k2是该方程的两个根,所以k1k2==−1,整理得:

当题设中的两条直线斜率不存在或为0 时,点A的坐标满足方程②.
综上所述,点A的轨迹方程为:x2+y2=7.同理,B,C,D的轨迹方程也为:x2+y2=7.即A,B,C,D四点在以原点为圆心,为半径的圆上.所以四边形ABCD是以原点为圆心,为半径的圆的内接矩形,只有当ABCD为正方形时面积最大,可得最大值SABCD=14.
妙解由定理可知,四边形ABCD的顶点是在椭圆的蒙日圆上,其轨迹方程为:x2+y2=7.所以结合基本不等式等知识可知只有当ABCD为正方形时面积最大,最大值SABCD=14.
评析此题的妙解可谓是把蒙日圆解题的优势体现地淋漓尽致! 通法实际上是把“四边形ABCD的顶点是在椭圆的蒙日圆上”这个结论给证明了一遍,作为一个小题,这样处理实在是得不偿失,但这是在不知道结论的情况下的不得已而为之.其实高考就曾经以椭圆的蒙日圆为背景考查过大题,大家不妨参阅2014年高考广东卷理科第20 题.
结语笛卡尔说过:“我所解决的每一个问题都将成为一个范例,以用于解其他问题”.为了应对高考,每天庞大的题量给学生的心理带来了很大的负担和压力,给学生减负于我们而言责无旁贷.因此,我们只有跳进题海,善于对同一类问题做深入的研究和总结,做到触类旁通,才能让学生跳出题海,才能在解题时化难为易,化繁为简.像利用蒙日圆和阿氏圆等这类隐形圆进行解题教学,不仅可以让学生在解题中直接获益,更可以培养其分析和解决问题的能力,从而提升其数学的解题素养.
