突破·优化·感悟

孔忠伟

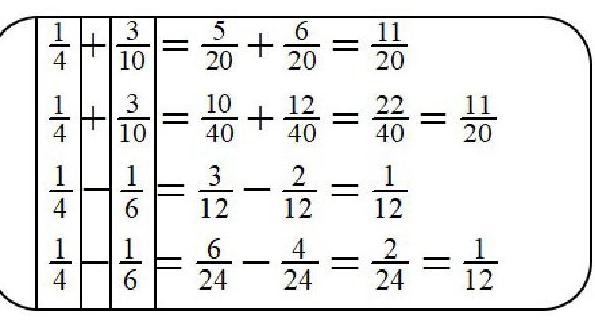
【摘   要】好的计算教学需要精巧深度的教学设计，同时也需要灵动有效的课堂处理，特别是教师要善于及时抓住合理有效的生成，引导学生突破计算教学的重难点，感悟算理。从“替身”一词出发，深度分析教学现象，并以此来整理和思考教材的相关内容，能帮助教师寻找到有效的计算教学策略。

【关键词】算法与算理;替身;计算教学

“替身”，一般是指在电视或电影拍摄过程中代替别人来演戏的人。那么在我们的计算课堂中，有替身吗？答案是肯定的。“替身”不仅存在于真实的课堂中，而且在我们的数学教材中都有它的影子。只要教师做个有心人，不断地去寻找它，运用它，“替身”就一定可以让计算教学焕发光彩。

【案例呈现】

请看一位教师教学人教版五年级下册“异分母分数加、减法”片段。

（课件展示）

师：刚才我们解决了这些计算题，现在再一起来看一下。老师有一个疑问，这些计算中都有[14]，但在运算过程中却都没有出现[14]。比如，第1题，它派了[520]来计算。你们看一看，这些分数与[14]有什么联系吗？

生：这些分数的大小都是一样的。

生：这样是为了使两个分数的分母变一样。

生：我感觉，[520]就像是[14]的“替身”。

师：哦！这位同学提到了“替身”，这个词我喜欢，好像是有那点味道，你同意吗？（板书：替身）那为什么要派“替身”呢？

生：为了更好地进行计算。

师：那你来说说，怎么就可以更好地计算了？

生：因为这两个分数的分母不一样，有了替身后，就可以找到两个分母都一样的分数来相加。

师：哦，那你的意思就是两个分数都要找“替身”，才能相加。如果把后面的这些分数叫“替身”，那么前面的分数就是什么呢？

生：真身。

師：那么“真身”怎么转化成“替身”呢？

生：其实就是把两个分数先通分，然后再计算。

生：就是需要把异分母转化成同分母。

生：一般分母找它们的最小公倍数就可以了。

……

师：哦！同学们太厉害了。把异分母的“真身”进行通分，转化成同分母的“替身”就可以了。（板书）

【案例反思】

此教学环节中，学生积极参与，课堂氛围非常好，同时运算的本质也在学生的辩论中越来越清晰。课后，笔者在感叹执教者灵动、有效的课堂调控力的同时，也对“替身”一词产生了浓厚的兴趣。带着种种问题，笔者从教材和教学等角度展开分析。

（一）为什么可以有替身？

在以上教学片段中，教师一句“你们看一看，这些分数与[14]有什么联系吗”，引导学生产生了“替身”的想法。这看似教师有意的引导，实则却是学生自然的流露。因为在异分母分数加减法中，把不同的分数转换成同分母分数的过程，就与寻找替身的过程不谋而合，而后者更加显得形象和有趣。把异分母分数转换成同分母分数，就是利用分数的基本性质不断寻找等值分数的过程，因为任何一个分数都有无数个等值分数，也就是有无数个“替身”。学生只有真正寻找到合适的替身，才能快速计算。因此，出现替身并讨论替身显得合情合理。

（二）替身对教学有何价值？

课程标准提倡启发式学习。教师如果直接引导学生去观察其中的算法，相信也能较好地完成教学任务。但真正的启发式教学，就需要让学生在主动参与、不断思辨中思考问题，学习知识。因此，在教学过程中，教师开展对“替身”的讨论、比较、归纳等活动，看似在讨论“替身”，其实质就是在不断启发学生。因此笔者认为“替身”是教学的一种媒介，通过它可以更好地引导学生关注知识的本质，感悟数学思想。同时“替身”也是一种艺术，在教师细腻的处理下，学生的学习兴趣被不断激发，教学效率得到了提升。

【策略探寻】

从这节课出发，笔者整理了人教版教材中有关计算教学的内容，发现计算教学中存在不少“替身”，而这些替身在计算教学中发挥着重要的作用，了解它们并合理地利用替身来改进教学，可以让计算教学焕发更多光彩。

（一）梳理教材，寻找替身

通过整理，笔者发现有关替身的内容主要存在于小学数学中高段的教学中（见表1）。

（二）基于替身，寻找策略

仔细分析这些内容，笔者发现计算教学中“替身”大致可以分成三类。一类是必须借助替身才能计算，另一类是借助替身可以优化算法，最后一类是借助替身可以帮助理解算理等。而不同的情况，教师需要不同对待，从而更好地提升计算教学的效率。

1.基于替身，突破难点教学

通过教材梳理，笔者发现在人教版教材中，有部分内容必须借助替身来完成计算，而在这些计算中，寻找替身的过程往往就是计算的难点。教师能够关注这个关键的环节，对于帮助学生突破难点、掌握算法，有一定的价值。

比如：教学小数除法、异分母分数加减、分数的除法等。

从上图可以发现，不管是小数除法还是异分母分数的加法，都必须转换成其他一个数来完成计算，而这个数就是它们的替身。而转换的过程，也正是计算教学的难点。比如小数的除法，往往需要把除数转变成整数，小数点的移动则是学生容易出错的地方。又比如在分数的除法中，转换成同分母，寻找最小公倍数也是本课的难点。因此，通过关注替身的讨论，能够引导学生展开计算难点的交流，并有效引导学生认识这些转换的关键，突破计算教学的难点，提升计算教学的效率。

2.基于替身，优化算法教学

《义务教育数学课程标准（2011年版）》指出，在运算能力的培养中需要引导学生寻找简洁有效的方法来开展计算。因此，在计算教学中，关注计算的优化教学，鼓励学生寻求简洁的算法，是教师需要不断渗透的目标之一。笔者发现在数的运算过程中，有些计算可以用替身，也可以不用替身，但如果借助了替身，则可以帮助学生更好地优化算法，提升计算的正确率。

比如：教学“小数的加减法和简便运算”。

在上图中，3.60就是3.6的替身。在小数减法中，通过这个替身，就可以帮助学生更好地开展计算，从而提升小数计算的正确率。再比如，简便计算中，4和8就是32的替身……通过这样的替换，就可以巧妙地把一些方法进行整合，同时渗透凑整的思想，也让学生明白“有些替身之间也有相互的伙伴”等，从而增强学生简算的意识，提升运算能力。

3.基于替身，感悟理解算理

计算教学需要特别关注算法和算理之间的联系，教师往往会通过数形结合的方式来直观呈现算理，并沟通不同算法之间的关系，来帮助学生理解算理。而同样，我们也可以借助找替身来帮助学生理解算理。

比如：教学除数是整十数的笔算除法。

228元平均分给30人，每人分到多少元？

228÷30=7（元）……18（元）

在上面的除数是整十数的笔算除法学习中，学生一般都能掌握其中的算法，即当前两位不够除以除数时，需要用前三位去除以除数，但至于为什么要这样算，背后的算理是什么，学生则感悟不深。因此，在新知教学中，教师可以借助人民币，引导学生思考“直接用22张10元分，不能直接分给30人时，该怎么办？”学生通过转化，得出可以换成220个1元来计算。而220个1元就是22个10元的替身，它可以帮助学生更好地理解其中的道理。因此，教师需要关注这样的替身转换，帮助学生感悟其中的算理，提升算法。

希尔伯特说：“当我听别人讲解某些数学问题时，常觉得很难理解，甚至不可能理解。这时便想，是否可以将问题化简些呢？”的确，在计算教学中，面对有些内容讲不清、理不通、记不牢时，教师可以思考能否借助一些灵活的内容来替换，从而让计算教学焕发新的光彩。

参考文献：

[1]喻佐成.用学具化难为易：以《异分母分数加减法》教学为例[J].湖北教育（教育教学），2016（11）.

（浙江省杭州市钱江湾小学   310000）